It is known that power series expansion of certain functions such as sech⁡(x) diverges beyond a finite radius of convergence. We present here an iterative power series expansion (IPS) to obtain a power series representation of sech⁡(x) that is convergent for all x. The convergent series is a sum of the Taylor series of sech⁡(x) and a complementary series that cancels the divergence of the Taylor series for x ≥ π/2. The method is general and can be applied to other functions known to have finite radius of convergence, such as 1/(1 + x²). A straightforward application of this method is to solve analytically nonlinear differential equations, which we also illustrate here. The method provides also a robust and very efficient numerical algorithm for solving nonlinear differential equations numerically. A detailed comparison with the fourth-order Runge-Kutta method and extensive analysis of the behavior of the error and CPU time are performed.

1. Introduction

It is well-known that the Taylor series of some functions diverge beyond a finite radius of convergence [1]. For instance, by way of example not exhaustive enumeration, the Taylor series of sech⁡(x) and 1/(1 + x²) diverge for x ≥ π/2 and x ≥ 1, respectively. Increasing the number of terms in the power series does not increase the radius of convergence; it only makes the divergence sharper. The radius of convergence can be increased only slightly via some functional transforms [2]. Among the many different methods of solving nonlinear differential equations [3–9], the power series is the most straightforward and efficient [10]. It has been used as a powerful numerical scheme for many problems [11–19] including chaotic systems [20–23]. Many numerical algorithms and codes have been developed based on this method [10–12, 20–24]. However, the above-mentioned finiteness of radius of convergence is a serious problem that hinders the use of this method to wide class of differential equations, in particular the nonlinear ones. For instance, the nonlinear Schrödinger equation (NLSE) with cubic nonlinearity has the sech⁡(x) as a solution. Using the power series method to solve this equation produces the power series of a sech⁡(x), which is valid only for x < π/2.

A review of the literature reveals that the power series expansion was exploited by several researchers [10–12, 20–24] to develop powerful numerical methods for solving nonlinear differential equations. Therefore, this paper is motivated by a desire to extend these attempts to a develop a numerical scheme with systematic control on the accuracy and error. Specifically, two main advances are presented in this paper: (1) a method of constructing a convergent power series representation of a given function with an arbitrarily large radius of convergence and (2) a method of obtaining analytic power series solution of a given nonlinear differential equation that is free from the finite radius of convergence. Through this paper, we show robustness and efficiency of the method via a number of examples including the chaotic Lorenz system [25] and the NLSE. Therefore, solving the problem of finite radius of convergence will open the door wide for applying the power series method to much larger class of differential equations, particularly the nonlinear ones.

It is worth mentioning that the literature includes several semianalytical methods for solving nonlinear differential equations; such as homotopy analysis method (HAM), homotopy perturbation method (HPM), and Adomian decomposition method (ADM); for more details see [26–29] and the references therein. Essentially, these methods generate iteratively a series solution for the nonlinear systems where we have to solve a linear differential equation at each iteration. Although these methods prove to be effective in solving most of nonlinear differential equations and in obtaining a convergent series solution, they have few disadvantages such as the large number of terms in the solution as the number of iterations increases. One of the most important advantages of the present technique is the simplicity in transforming the nonlinear differential equation into a set of simple algebraic difference equations which can be easily solved.

The paper is thus divided into two, seemingly separated, but actually connected main parts. In the first (Section 2), we show, for a given function, how a convergent power series is constructed out of the nonconverging one. In the second part (Section 3.1), we essentially use this idea to solve nonlinear differential equations. In Section 3.2, we investigate the robustness and efficiency of the method by studying the behavior of its error and CPU time versus the parameters of the method. We summarise our results in Section 4.

2. Iterative Power Series Method

This section describes how to obtain a convergent power series for a given function that is otherwise not converging for all x. In brief, the method is described as follows. We expand the function f(x) in a power series as usual, say around x = 0. Then we reexpress the coefficients, f⁽ⁿ⁾(x), in terms of f(x). This establishes a recursion relation between the higher-order coefficients, f⁽ⁿ⁾(0), and the lowest order ones, f⁽⁰⁾(0) and f⁽¹⁾(0), and thus the power series is written in terms of only these two coefficients. Then the series and its derivative are calculated at x = Δ, where Δ is much less than the radius of convergence of the power series. A new power series expansion of f(x) is then performed at x = Δ. Similarly, the higher-order coefficients are reexpressed in terms of the lowest order coefficients f⁽⁰⁾(Δ) and f⁽¹⁾(Δ). The value of the previous series and its derivative calculated at x = Δ are then given to f⁽⁰⁾(Δ) and f⁽¹⁾(Δ), respectively. Then a new expansion around 2Δ is performed with the lowest order coefficients being taken from the previous series, and so on. This iterative process is repeated N times. The final series will correspond to a convergent series at x = NΔ.

Here is a detailed description of the method. The function f(x) is expanded in a Taylor series, T⁰(x), around x = 0. The infinite Taylor series is an exact representation of f(x) for x < R where R is the radius of convergence. For x ≥ R the series diverges. We assume that x is divided into N small intervals Δ = x/N such that Δ < R. Expanding f(x) around the beginning of each interval we obtain N convergent Taylor series representing f(x) in each interval

()

where T^j(y) denotes the Taylor series expansion of f(y) around y = jΔ and f⁽ⁿ⁾(jΔ) is the nth derivative of f(y) calculated at y = jΔ. It is noted that we use y ∈ [(j − 1)Δ, jΔ] as the independent variable for the nth Taylor series expansion to distinguish it from x = NΔ. However, these series can not be combined in a single series since their ranges of applicability are different and do not overlap. To obtain a single convergent power series out of the set of series T^j, we put forward two new ideas, which constitute the basis of our method; namely:

(1) Reexpress f⁽ⁿ⁾(y) in terms of f(y) as f⁽ⁿ⁾(y) = F_n[f(y)], where the functional F_n[f(y)] is determined by direct differentiation of f(y) for n times and then reexpressing the result in terms of f(y) only. We conjecture that this is possible for a wide class of functions if not all. At least for the two specific functions considered here, this turned out to be possible. Equation (1) then takes the form

()

where we have renamed f(jΔ) by

and F_n[f(jΔ)]/n! by

for a reason to be obvious in the next section. Thus, the coefficients a_n for all n are determined only by

(2) Calculate

from T^j−1 at jΔ

()

which amounts to assigning the value of the Taylor series at the end of an interval to

of the consecutive one. Equation (3) captures the essence of the recursive feature of our method;

is calculated recursively from

by repeated action of the right-hand-side on

. While T^j represents the function f within an interval of width Δ, the sequence

corresponds to the values of the function at the end of the intervals. In the limit N → ∞, or equivalently Δ → 0, the discrete set of

values and jΔ render to the continuous function f(x) and its independent variable x, respectively. Formally, the convergent power series expansion of f(x) around x = 0 will thus be given by

()

where S^N denotes the N^th iteration of

()

As an illustrative example, we apply the method to f(x) = sech⁡(x). The infinite Taylor series expansion of this function diverges sharply to infinity at x = π/2. The first step is to determine the coefficients

, which are the coefficients of the T^j series

()

The next step is to reexpress the higher-order coefficients,

, in terms of the zeroth-order coefficient

. The property sech²⁡(y) + tanh²⁡(y) = 1 is used to that end. It is noticed, however, that while it is possible to express the even-n coefficients in terms of

only, the odd-n coefficients can only be expressed terms of both

and

. In the context of solving differential equations using the power series method, this reflects the fact that the solution is expressed in terms of two independent parameters (initial conditions). The sech function is indeed a solution of a second-order differential equation, which is solved using this method in the next section. Equation (6) then takes the form

()

Calculating T^j(y) series at the end of its interval of applicability, y = (j + 1)Δ, we get

()

where the “recursion” coefficients are given by

()

Finally, we assign T^j((j + 1)Δ) to

()

The second independent coefficient

is determined by the derivative of T^j(y) calculated at y = (j + 1)Δ

()

While, in the limit N → ∞,

corresponds to the function f(x), the sequence

corresponds to f^′(x). Therefore, the power series expansion of sech⁡(x) and its first derivative are given by

()

where the superscript of the matrix on the right-hand-side, N, denotes the Nth iteration of the matrix. The superscript j has been removed since the functional form of the recursion coefficients does not depend on j. The procedure of calculating the power series recursively is described as follows. First, a₀ = sech⁡(0) = 1 and a₁ = sech^′⁡(0) = 0 are substituted in the right-hand-side of the last equation. Then the result of the upper element is taken as the updated value of a₀, and, similarly, the lower element updates a₁. The two updated values are then resubstituted back in the right-hand-side. The process is repeated N times. To obtain an explicit form of the series we truncate the Taylor series at n_max = 4 and use N = 4 iterations. The resulting expansion takes the form

()

It is noted that the higher-order coefficients, which correspond to ratios of large integers, are represented in real numbers for convenience. Already with such a small number of iterations, N = 4, the number of terms equals 313. By inspection, we find that the number of terms equals ((n_max + 1) ^N + 1)/2. Here, n_max is even due to the fact that sech⁡(x) is an even function.

It is also noted that the series (13) is composed of the Taylor expansion of sech⁡(x) around zero, represented by the first three terms, and a series of higher-order terms generated from the nonlinearity in the recursion relations of a_n. In fact, we prove in the next section that this property holds for any n_max, N, and function f(x), provided that the Taylor series of the later exists. Therefore, the power series expansion of sech⁡(x), given by (12), can be put in the suggestive form

()

where T is the infinite Taylor series of f(x) about x = 0 and C(N) is a complementary series. It turns out that the complementary series increases the radius of convergence of T for x ≥ π/2. For finite N, the effect of C(N) is to shift the radius of convergence, R, to a larger value such that R → ∞ for N → ∞. In Figure 1 we plot the convergent power series obtained by the present method as given by (12) using n_max = 4 and N = 100. The curve is indistinguishable from the plot of sech⁡(x). Both the Taylor series expansion, T, and the complementary series, C, diverge sharply at x = π/2. Since C is essentially zero for x < π/2, it will not affect the sum T + C. However, its major role is to cancel the divergency for x ≥ π/2. In the limit N → ∞, T will be an exact representative of sech⁡(x) for x < π/2 and C will equal zero in the same interval. For x ≥ π/2, the divergences in T and C cancel each other with a remainder that is an exact representative of sech⁡(x). In this manner, T + C will represent sech⁡(x) for all x.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The solid curve corresponds to the convergent power series obtained by the present method as given by (12) using n_max = 4 and N = 100. It is indistinguishable from the solid curve of f(x) = sech⁡(x). Dashed curve corresponds to the Taylor series expansion, T, and the dotted curve corresponds to the complementary series, C.

For finite values of n_max and N, the series T + C is an approximate representative of sech⁡(x). Truncating the Taylor series at n_max introduces an error of order

. This error will be magnified N times due the recursive substitutions. The total error is then estimated by

()

For the parameters used in Figure 1, this error is of order 10⁻⁶ at x = 5. This can be reduced to extremely small values such as 10⁻¹³¹ with n_max = 100. However, the number of terms in the series T + C will be of order 10²⁰⁰ which is extremely large and hinders any analytical manipulations.

As another example, we consider f(x) = 1/(1 + x²) with Taylor series diverging at x = 1. Much of the formulation we followed for the previous case holds here and the specifics of the function alter only the recursion relations, (9):

()

The convergent power series is obtained by using these recursion relations in (12). Plots similar to those of Figure 1 are obtained.

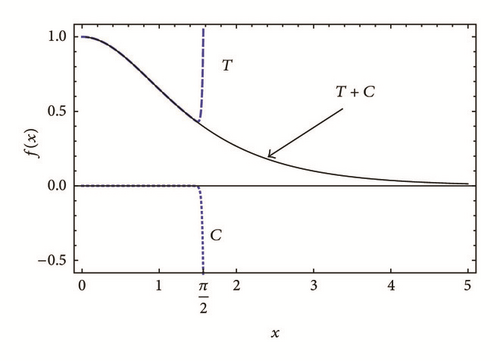
We present now a proof that the convergent power series produced by the recursive procedure always regenerates the Taylor series in addition to a complementary one.

Proposition 1. If we expand f(x) in a Taylor series, T, around x = 0 truncated at n_max and use the recursive procedure, as described above, the resulting convergent power series always takes the form T + C where C is a power series of orders larger than n_max. This is true for any number of iterations, N, maximum power of the Taylor series, n_max, and for all functions that satisfy the general differential equation

()

where F[·] is an analytic real functional that does not contain derivatives.

Proof. It is trivial to prove this for a specific case, such as sech⁡(x). For the general case, we prove this only for n_max = 4 and N = 2. The Taylor series expansion of sech⁡(x) around x = 0 is

()

In our recursive procedure, this is put in the equivalent form

()

where the approximation stems from using finite N and n_max, and Δ = x/N. For N = 1, a₀ = 1, and a₁ = 0, (20) is regenerated. However, in our recursive procedure a₀ and a₁ are kept as variables since they will be substituted for at each recursive step. Only at the last step are their numerical values inserted. For N = 2, we resubstitute in the last equation for a₀ and a₁ by their updated expressions, as follows:

()

Substituting the updated expressions for a₀ and a₁ in (21), we get

()

Clearly for N = 2, the last equation gives the Taylor expansion, that is, (21) with N = 1. The complimentary series, C, is absent here since we have terminated the expansions at n = n_max = 4. For N = 3, another step of resubstituting updated expressions is needed, and so on.

Now, we present the proof for the more general case, namely, when f(x) is unspecified but is a solution to (19). We start with the following Taylor series expansion of f(x) and its derivative

()

Substituting on the right-hand-side for a₀ and a₁ by f(Δ) and f^′(Δ), respectively, we get

()

The partial derivatives can not be calculated unless the functional forms of the recursion coefficients are known. One possibility is to specify the function being expanded, f(x), as we did at the start of this proof. The other possibility is to exploit the differential equation that f(x) is a solution for, namely, (19). Substituting the Taylor expansion of f(Δ), from (24) in (19) and expanding up to the fourth power in Δ, we obtain the following relations:

()

which lead to

()

Using these equations in (28), we obtain

()

For N = 2, the last equation regenerates the Taylor series of f(x), namely, (24) with N = 1, and this completes the proof.

3. Application to Nonlinear Differential Equations

The method described in the previous section can be used as a powerful solver and integrator of nonlinear differential equations both analytically and numerically. In Section 3.1, we apply the method on a number of well-known problems. In Section 3.2, we show the power of the method in terms of detailed analysis of the error and CPU time.

3.1. Examples

For the sake of demonstration, we consider the following nonlinear differential equation:

()

The reason for selecting this equation is that f(x) = sech⁡(x) is one of its exact solutions. Substituting the power series expansion

, we obtain, as usual, the recursion relations

()

where a₀ and a₁ turn out to be independent parameters which in the present case correspond to the initial conditions on the solution and its first derivative. It is not surprising that these recursion relations are identical with those we found for the sech⁡(x) in the previous section, (9). Therefore, substituting the above recursion relations in

we obtain the Taylor series expansion, T, of f(x) = sech⁡(x). Removing the divergency in T follows exactly the same steps as in the previous section, and thus an exact solution in terms of a convergent power series is obtained, as also plotted in Figure 1.

For f(x) = 1/(1 + x²), the relevant differential equation is

()

Substituting the power series expansion in this equation, the recursion relations will be given by (16)–(18). Similarly, the convergent series solution will be obtained, as in the previous section.

3.2. Numerical Method

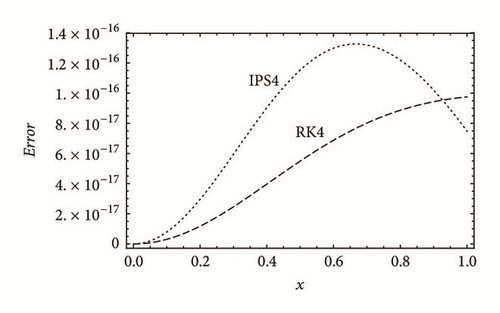
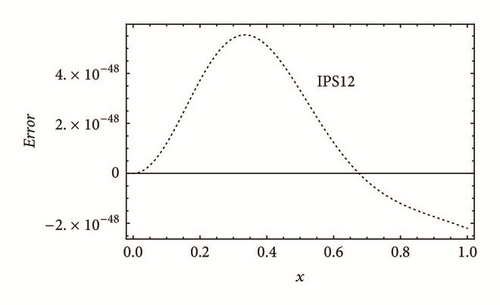
As a numerical method, the power series is very powerful and efficient [10]. The power series method with N_max = 4, denoted by IPS4, is used to solve the NLSE, (29) and the error is calculated as the difference between the numerical solution and the exact solution, namely, sech⁡(x). The equation is then resolved using the fourth-order Runge-Kutta (RK4) method. In Figure 2, we plot the error of both methods which turn out to be of the same order. Using the iterative power series method with N_max = 12, (IPS12), the error drops to infinitesimally low values. Neither the CPU time nor the memory requirements for IPS12 are much larger than those for IPS4; it is straight forward upgrade to higher orders which leads to ultrahigh efficiency. This is verified by the set of tables, Tables 1–4, where we compute sech⁡(1) using both the RK4 and the iterative power series method and show the corresponding CPU time. For the same N, Tables 1 and 3 show that both RK4 and IPS4 produce the first 16 digits of the exact value (underlined numbers in the last raw) and consume almost the same CPU time. Table 3 shows that, for the same N, IPS12, reproduces the first 49 digits of the exact value. The CPU time needed for such ultrahigh accuracy is just about 3 times that of the RK4 and IPS4. Of course the accuracy can be arbitrarily increased by increasing N or more efficiently N_max. For IPS12 to produce only the first 16 digits, as in RK4 and IPS4, only very small number of iterations is needed, as shown in Table 4. The CPU time in this case is about 100 times less than that of RK4 and IPS4, highlighting the high efficiency of the power series method.

Table 1. RK4 sech⁡(x) solution of the NLSE, (29), computed at x = 1.

RK4
N	sech⁡(1)	CPU time
1000	0.6480542736639463753683598987682775440961395993015	0.087257
2000	0.6480542736638892102461002212645001242748400651983	0.166534
3000	0.6480542736638861522791729310382098086291071707752	0.229016
4000	0.6480542736638856377319630763886301512099763161750	0.314480
5000	0.6480542736638854971232600221160524143929321411426	0.427610
Exact	0.6480542736638853995749773532261503231084893120719

Table 2. IPS4 sech⁡(x) solution of the NLSE, (29), computed at x = 1.

IPS4
N	sech⁡(1)	CPU time
1000	0.6480542736639323955233350367786700400715255548373	0.056793
2000	0.6480542736638883277492809223389308596155602276884	0.137941
3000	0.6480542736638859773823119964459740185046024606302	0.215395
4000	0.6480542736638855823023023050565759829475356280281	0.304501
5000	0.6480542736638854743968579026604641270130595226186	0.372284
Exact	0.6480542736638853995749773532261503231084893120719

Table 3. IPS12 sech⁡(x) solution of the NLSE, (29), computed at x = 1.

IPS12
N	sech⁡(1)	CPU time
1000	0.6480542736638853995749773532261503231079594354079	0.280617
2000	0.6480542736638853995749773532261503231084891816361	0.595639
3000	0.6480542736638853995749773532261503231084893110634	0.891370
4000	0.6480542736638853995749773532261503231084893120400	1.080357
5000	0.6480542736638853995749773532261503231084893120697	1.366386
Exact	0.6480542736638853995749773532261503231084893120719

Table 4. IPS12 sech⁡(x) solution of the NLSE, (29), computed at x = 1, but with much less number of iterations than in Table 3.

IPS12
N	sech⁡(1)	CPU time
3	0.6480542794079665629469114154348980055814088430953	0.000782
6	0.6480542736643770346283969779587807646256058100135	0.001429
9	0.6480542736638872007452856567074697922787489590238	0.002123
12	0.6480542736638854259793573015747954030451932565027	0.002768
15	0.6480542736638854001495023257702479909741369016589	0.003594
Exact	0.6480542736638853995749773532261503231084893120719

A more challenging test on the power series method is the chaotic Lorenz system [25] given by

()

where we take the usual values σ = 10, b = −8/3, and R = 28 with initial conditions z₁(0) = z₂(0) = 1 and z₃(0) = 20. It is straight forward to generalise the method to three differential equations; therefore we do not show the details of the calculation. In Figure 3, the results of solving the Lorenz system using RK4 and IPS12 are shown. For the same parameters, namely discretization, RK4 reaches stability at about x = 30; that is, the curve for x < 30 is unchanged by increasing N, but for x > 30, the curve keeps changing by increasing N. In comparison, IPS12 reaches stability at about x = 50. In chaotic systems, it is quite challenging to go that deep in the chaotic region. Hence, the need for such high accuracy methods.

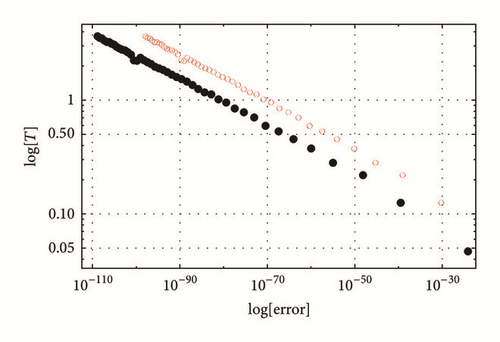
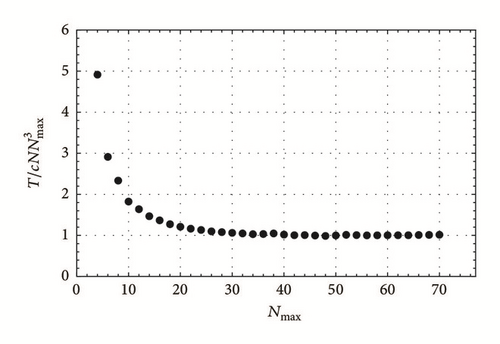
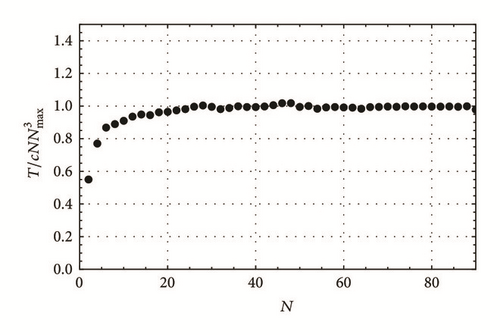
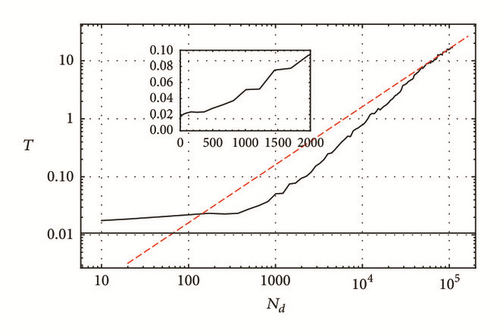
Achieving higher accuracy requires larger CPU time usage. Therefore, it is important to investigate how the CPU time, denoted here by T, depends on the main parameters of the method, namely N and N_max. A typical plot is shown in Figure 4, where we plot on a log-log scale the CPU time versus the error. The linear relationship indicates T ∝ error^p, where p is the slope of the line joining the points in Figure 4. The error can be calculated in two ways: (i) the difference between the numerical solution and (ii) theoretical estimate, (15). Both ways are shown in the figure and they have the same slope. However, as expected, error defined by (15), which is actually an upper limit on the error, is always larger than the first one. To find how the CPU time depends explicitly on N and N_max, we argue that the dependence should be of the form . This is justified by the fact that CPU time should be linearly proportional to the number of terms computed. The number of terms computed increases linearly with the number of iterations N. The number of terms in the power series is linearly proportional to N_max. When substituted in the NLSE with cubic nonlinearity, the resulting number of terms, and thus T, will be proportional to . In Figure 5, it is shown indeed that the ratio saturates asymptotically to a constant for large N and N_max since the scaling behaviors mentioned here apply for large N and N_max. The proportionality constant, c, is very small and corresponds to the CPU time of calculating one term. It is dependent on the machine, the programming optimization [10], and the number of digits used, N_d. In terms of the number of digits, the CPU time increases, as shown in Figure 6, where it is noticed that CPU time is almost constant for number of digits N_d < 500.

4. Conclusions

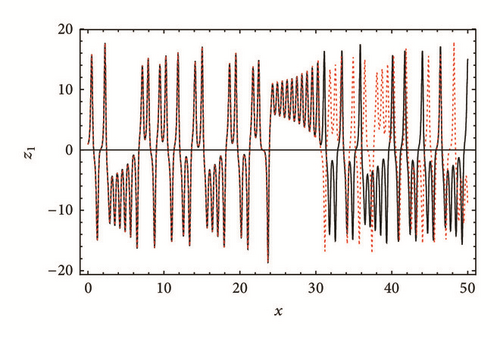
We have presented an iterative power series method that solves the problem of finite radius of convergence. We have proved that the iterative power series is always composed of a sum of the typical power series of the function and a complementary series that cancels the divergency. The method is divided into two schemes where in the first we find a convergent power series for a given function and in the second we solve a given nonlinear differential equation. The result of the iterative power series expansion of sech⁡(x) is remarkably convergent for arbitrary radius of convergence and accuracy, as shown by Figures 1 and 2 and Tables 1–4. Extremely high accuracy can be obtained by using higher-order iterative power series via increasing N_max with relatively low CPU time usage. Robustness and efficiency of the method have been shown by solving the chaotic Lorenz system and the NLSE. Extensive analysis of the error and CPU time characterising the method is performed. Although we have focused on the localised sech⁡(x) solution of the NLSE, all other solitary wave solutions (conoidal waves) can be obtained using the present method, just by choosing the appropriate initial conditions.

The method can be generalised to partial and fractional differential equations making its domain of applicability even wider.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

References

1 Abramowitz M. and Stegun I. A., Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 1965, 7, Dover Publications, New York, NY, USA, https://doi.org/10.2307/1266136.
Google Scholar
2 Scraton R. E., A note on the summation of divergent power series, Mathematical Proc. of the Camb. Phil. Soc. (1969) 66, 109–114, MR0244667.
10.1017/S0305004100044765
Web of Science® Google Scholar
3 Polyanin A. D. and Zaitsev V. F., Handbook of Nonlinear Partial Differential Equations, 2003, Chapman and Hall, New York, NY, USA, MR2042347, Zbl1053.35001.
10.1201/9780203489659
Google Scholar
4 Gardner C. S., Greene J. M., Kruskal M. D., and Miura R. M., Method for solving the Korteweg-deVries equation, Physical Review Letters. (1967) 19, no. 19, 1095–1097, https://doi.org/10.1103/PhysRevLett.19.1095, 2-s2.0-36049057587.
10.1103/PhysRevLett.19.1095
CAS Web of Science® Google Scholar
5 Lax P. D., Integrals of nonlinear equations of evolution and solitary waves, Communications on Pure and Applied Mathematics. (1968) 21, 467–490, MR0235310, https://doi.org/10.1002/cpa.3160210503, 2-s2.0-84981754671.
10.1002/cpa.3160210503
Web of Science® Google Scholar
6 Matveev V. B. and Salle M. A., Darboux Transformations and Solitons, 1991, Springer-Verlag, Berlin, Gemany, https://doi.org/10.1007/978-3-662-00922-2, MR1146435.
10.1007/978-3-662-00922-2
Google Scholar
7 Hirota R., R. K. Eullough and P. I. Caudrey, Topics in Current Physics 17, 1980, Springer-Verlag, Berlin, Germany.
Google Scholar
8 Adomian G., Solving Frontier Problems of Physics: The Decomposition Method, 1994, Kluwer Academic, Dordrecht, The Netherlands, https://doi.org/10.1007/978-94-015-8289-6, MR1282283, Zbl0802.65122.
10.1007/978-94-015-8289-6
Google Scholar
9 Liao S. and Tan Y., A general approach to obtain series solutions of nonlinear differential equations, Studies in Applied Mathematics. (2007) 119, no. 4, 297–354, MR2358643, https://doi.org/10.1111/j.1467-9590.2007.00387.x, 2-s2.0-34848900880.
10.1111/j.1467-9590.2007.00387.x
Web of Science® Google Scholar
10 Barrio R., Rodríguez M., Abad A., and Blesa F., Breaking the limits: the Taylor series method, Applied Mathematics and Computation. (2011) 217, no. 20, 7940–7954, https://doi.org/10.1016/j.amc.2011.02.080, MR2802205.
10.1016/j.amc.2011.02.080
Web of Science® Google Scholar
11 Corliss G. and Chang Y. F., Solving ordinary differential equations using Taylor series, ACM Transactions on Mathematical Software. (1982) 8, no. 2, 114–144, MR661124, https://doi.org/10.1145/355993.355995, 2-s2.0-0020143282.
10.1145/355993.355995
Web of Science® Google Scholar
12 Chang Y. F. and Corliss G., ATOMFT: solving ODEs and DAEs using Taylor series, Computers & Mathematics with Applications. (1994) 28, no. 10-12, 209–233, 2-s2.0-0040763312, https://doi.org/10.1016/0898-1221(94)00193-6.
10.1016/0898-1221(94)00193-6
Web of Science® Google Scholar
13 Pryce J. D., Solving high-index DAEs by Taylor series, Numerical Algorithms. (1998) 19, no. 1-4, 195–211, https://doi.org/10.1023/A:1019150322187, MR1668299.
10.1023/A:1019150322187
Web of Science® Google Scholar
14 Barrio R., Performance of the Taylor series method for ODEs/DAEs, Applied Mathematics and Computation. (2005) 163, no. 2, 525–545, https://doi.org/10.1016/j.amc.2004.02.015, MR2121808.
10.1016/j.amc.2004.02.015
Web of Science® Google Scholar
15 Nedialkov N. S. and Pryce J. D., Solving differential-algebraic equations by taylor series (I): Computing taylor coefficients, BIT Numerical Mathematics. (2005) 45, no. 3, 561–591, https://doi.org/10.1007/s10543-005-0019-y, 2-s2.0-28144454918.
10.1007/s10543-005-0019-y
Web of Science® Google Scholar
16 Nedialkov N. S. and Pryce J. D., Solving differential-algebraic equations by Taylor series. (II): Computing the system Jacobian, BIT Numerical Mathematics. (2007) 47, no. 1, 121–135, https://doi.org/10.1007/s10543-006-0106-8, MR2312500.
10.1007/s10543-006-0106-8
Web of Science® Google Scholar
17 Nedialkov N. S. and Pryce J. D., Solving differential algebraic equations by Taylor series. (III): THE DAETS code, JNAIAM. Journal of Numerical Analysis, Industrial and Applied Mathematics. (2008) 3, no. 1-2, 61–80, MR2435772.
Google Scholar
18 Nedialkov N. S., Jackson K. R., and Corliss G. F., Validated solutions of initial value problems for ordinary differential equations, Applied Mathematics and Computation. (1999) 105, no. 1, 21–68, MR1706055, https://doi.org/10.1016/S0096-3003(98)10083-8, 2-s2.0-0002265766.
10.1016/S0096-3003(98)10083-8
Web of Science® Google Scholar
19 Tucker W., A Rigorous ODE Solver and Smale′s 14th Problem, Foundations of Computational Mathematics. (2002) 2, no. 1, 53–117, 2-s2.0-0002061016, https://doi.org/10.1007/s002080010018.
10.1007/s002080010018
Web of Science® Google Scholar
20 Barrio R. and Blesa F., Systematic search of symmetric periodic orbits in 2DOF Hamiltonian systems, Chaos, Solitons & Fractals. (2009) 41, no. 2, 560–582, https://doi.org/10.1016/j.chaos.2008.02.032, MR2535606.
10.1016/j.chaos.2008.02.032
Web of Science® Google Scholar
21 Barrio R., Blesa F., and Serrano S., Periodic, escape and chaotic orbits in the Copenhagen and the (n+1)-body ring problems, Communications in Nonlinear Science and Numerical Simulation. (2009) 14, no. 5, 2229–2238, https://doi.org/10.1016/j.cnsns.2008.07.007, MR2474473.
10.1016/j.cnsns.2008.07.007
Web of Science® Google Scholar
22 Barrio R., Painting chaos: a gallery of sensitivity plots of classical problems, International Journal of Bifurcation and Chaos. (2006) 16, no. 10, 2777–2798, MR2282903, https://doi.org/10.1142/S021812740601646X.
10.1142/S021812740601646X
Web of Science® Google Scholar
23 Barrio R. and Serrano S., A three-parametric study of the Lorenz model, Physica D: Nonlinear Phenomena. (2007) 229, no. 1, 43–51, MR2340178, https://doi.org/10.1016/j.physd.2007.03.013, 2-s2.0-34247637165.
10.1016/j.physd.2007.03.013
Web of Science® Google Scholar
24 Jorba Á. and Zou M., A software package for the numerical integration of ODEs by means of high-order Taylor methods, Experimental Mathematics. (2005) 14, no. 1, 99–117, https://doi.org/10.1080/10586458.2005.10128904, MR2146523.
10.1080/10586458.2005.10128904
Web of Science® Google Scholar
25 Lorenz E., Deterministic nonperiodic flow, Journal of Atomic and Molecular Sciences. (1963) 20, 130–141.
10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2
Google Scholar
26 Allan F. M., Derivation of the Adomian decomposition method using the homotopy analysis method, Applied Mathematics and Computation. (2007) 190, no. 1, 6–14, MR2335425, https://doi.org/10.1016/j.amc.2006.12.074.
10.1016/j.amc.2006.12.074
Web of Science® Google Scholar
27 Al-Mdallal Q. M., Syam M. I., and Ariel P., Extended homotopy perturbation method and the axisymmetric flow past a porous stretching sheet, International Journal for Numerical Methods in Fluids. (2012) 69, no. 5, 909–925, MR2925535, https://doi.org/10.1002/fld.2619, 2-s2.0-84860557810.
10.1002/fld.2619
Web of Science® Google Scholar
28 Hajji M. A. and Al-Khaled K., Analytic studies and numerical simulations of the generalized Boussinesq equation, Applied Mathematics and Computation. (2007) 191, no. 2, 320–333, MR2385534, https://doi.org/10.1016/j.amc.2007.02.090, Zbl1193.35188, 2-s2.0-34548171726.
10.1016/j.amc.2007.02.090
Web of Science® Google Scholar
29 Liao S., On the homotopy analysis method for nonlinear problems, Applied Mathematics and Computation. (2004) 147, no. 2, 499–513, https://doi.org/10.1016/S0096-3003(02)00790-7, MR2012589, Zbl1086.35005, 2-s2.0-0141961626.
10.1016/S0096-3003(02)00790-7
Web of Science® Google Scholar

Citing Literature

All articles

Convergent Power Series of sech⁡(x) and Solutions to Nonlinear Differential Equations

Abstract

1. Introduction

2. Iterative Power Series Method

3. Application to Nonlinear Differential Equations

3.1. Examples

3.2. Numerical Method

4. Conclusions

Conflicts of Interest

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Convergent Power Series of sech⁡(x) and Solutions to Nonlinear Differential Equations

Abstract

1. Introduction

2. Iterative Power Series Method

3. Application to Nonlinear Differential Equations

3.1. Examples

3.2. Numerical Method

4. Conclusions

Conflicts of Interest

References

Citing Literature

Figures

References

Related

Information