In this paper, we consider a priori error estimates for the finite volume element schemes of optimal control problems, which are governed by linear elliptic partial differential equation. The variational discretization approach is used to deal with the control. The error estimation shows that the combination of variational discretization and finite volume element formulation allows optimal convergence. Numerical results are provided to support our theoretical analysis.

1. Introduction

In recent years, the optimization with partial differential equation constraints (PDEs) has received a significant impulse. Because of wide applicability of the field, a lot of theoretical results have been developed. Generally, it is difficult to obtain the analytical solutions for optimal control problems with PDEs. Factually, only approximate solutions or numerical solutions can be expected. Therefore, many numerical methods have been proposed to solve the problems.

Finite element method is an important numerical method for the problems of partial differential equations and widely used in the numerical solution of optimal control problems. There are extensive studies in convergence of finite element approximation for optimal control problems. For example, priori error estimates for finite element discretization of optimal control problems governed by elliptic equations are discussed in many publications. In [1], a new approach to error control and mesh adaptivity is described for the discretization of the optimal control problems governed by elliptic partial differential equations. In [2], the error estimates for semilinear elliptic optimal controls in the maximum norm are presented. Chen and Liu present a priori error analysis for mixed finite element approximation of quadratic optimal control problems [3]. In [4], a priori error analysis for the finite element discretization of the optimal control problems governed by elliptic state equations is considered. Hou and Li investigate the error estimates of mixed finite element methods for optimal control problems governed by general elliptic equations and derive L² and H¹ error estimates for both the control and state variables [5].

The finite volume element method has been one of the most commonly used numerical methods for solving partial differential equations. The advantages of the method are that the computational cost is less than finite element method, and the mass conservation law is maintained. So it has been extensively used in computational fluid dynamics [6–12]. However, there are only a few published results on the finite volume element method for the optimal control problems. In [13], the authors discussed distributed optimal control problems governed by elliptic equations by using the finite volume element methods. The variational discretization approach is used to deal with the control and the error estimates are obtained in some norms. In [14], the authors considered the convergence analysis of discontinuous finite volume methods applied to distributed optimal control problems governed by a class of second-order linear elliptic equations.

In this paper, we will investigate the finite volume element method for the general elliptic optimal control problem with Dirichlet or Neumann boundary conditions. The variational discretization approach is used to deal with the control, which can avoid explicit discretization of the control and improve the approximation. In addition, we discuss the optimal control problems in polygonal domains with corner singularities. In this situation, the solution does not admit integrable second derivatives. The desired convergence results of finite volume element schemes cannot be expected. Two effective methods are proposed to compensate the negative effects of the corner singularities. The corresponding results will be reported in the future.

The rest of the paper is organized as follows. In Section 2, the model problem and the finite volume element schemes are introduced. Section 3 presents the error estimates of the finite volume element schemes. In Section 4, numerical results are supplied to justify the theoretical analysis. Brief conclusions are given in Section 5.

2. Problem Statement and Discretization

2.1. Model Problem

In this paper, we consider the following second-order elliptic partial differential equation:

()

where Ω ⊂ R² is a bounded convex polygon with boundary ∂Ω, A = {a_ij(x)} is a 2 × 2 symmetric and uniformly positive definite matrix, c₀ > 0 is a sufficient smooth function defined on Ω, B denotes the linear and continuous control operator, Bu ∈ L²(Ω), and u and f have enough regularity so that this problem has a unique solution when we combine either homogeneous Dirichlet or Neumann boundary conditions on ∂Ω.

In addition, we use the following notations for the inner products and norms on L²(Ω), H¹(Ω), and L^∞(Ω):

()

The corresponding weak formulation for (1) is

()

where

()

and

()

H denotes either depending on the prescribed type of boundary conditions (homogeneous Neumann or Dirichlet).

Now, we consider the following optimal control problem for state variable y and the control variable u:

()

over all H × L²(Ω) subject to elliptic state problem (3) and the control constraints

()

where y_Ω ∈ L²(Ω) is a given desired state and λ ≥ 0 is a regularization parameter. We define the set of admissible control by

()

where U_ad is a nonempty, closed, and convex subset of L²(Ω),u_a(x) ≤ u_b(x).

From standard arguments for elliptic equations, we can obtain the following propositions.

Proposition 1. For fixed control u ∈ L²(Ω), the state equation (3) admits a unique solution y ∈ H. Moreover, there is a constant C, which does not depend on Bu + f, such that

()

Proposition 2. Let U_ad be a nonempty, closed, bounded, and convex set, y_Ω in L²(Ω) and λ > 0; then the optimal control problem (6) admits a unique solution .

This proof follows standard techniques [15].

The adjoint state equation for

is given by

()

where the equation is the weak formulation of the following elliptic problem:

()

with homogeneous Neumann or Dirichlet boundary conditions.

Proposition 3. The necessary and sufficient optimality conditions for (6) and (7) can be expressed as the variational inequality

()

Further, the variational inequality is equivalent to

()

where

denotes the orthogonal projection in L²(Ω) onto the admissible set of the control and B^∗ is the adjoint operator of B.

2.2. Discretization

Now we describe the finite volume element discretization of the optimal control problem (6).

We consider a quasi-uniform triangulation T_h. Divide into a sum of finite number of small triangles K such that they have no overlapping internal region and a vertex of any triangle does not belong to a side of any other triangle. At last, we can obtain a triangulation such that .

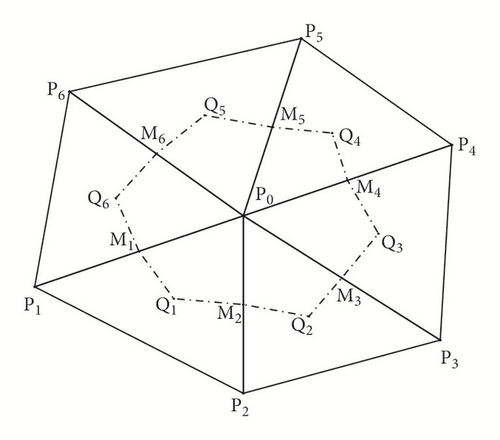
We then construct a dual mesh related to T_h. Let P₀ be a node of a triangle, P_i (i = 1,2, …, 6) the adjacent nodes of P₀, and M_i the midpoint of . Choose the barycenter Q_i of triangle ∆P₀P_iP_i+1 (P₇ = P₁) as the node of the dual mesh. Connect successively M₁, Q₁,…, M₆, Q₆, M₁ to form a polygonal region V, called a control volume. Figure 1 presents a sketch of a control volume.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Control volume with barycenter as internal point.

Let U_h be the trial function space defined on the triangulation T_h,

()

and V_h be the test function space defined on the dual mesh

()

In this way, we have

()

where ϕ_i are the standard node basis functions with the nodes x_i and ψ_i are the characteristic functions of the control volume V_i.

Let I_h and

be the interpolation projections onto the trial function space U_h and test function space V_h, respectively. By the interpolation theory, we have for w ∈ U_h∩H²

()

Then the finite volume element schemes for (3), (10), and (13) are defined as follows:

()

where

()

3. Error Estimates

In order to present the error estimates, we first introduce some lemmas in preparation of the proof for the main convergence theorem.

3.1. Some Lemmas

According to [16], we have the following lemma, which indicates that the bilinear form is coercive on U_h.

Lemma 4. is positive definite for small enough h; namely, there exist h₀ > 0, α > 0 such that for 0 < h ≤ h₀

()

We seldom have a symmetric bilinear form even though a(·, ·) is symmetric. The following lemma is used to measure how far the bilinear form is from being symmetric [17].

Lemma 5. There exist positive constants C, h₀ such that, for u, w ∈ U_h and 0 < h ≤ h₀, we have

()

Furthermore, we introduce the auxiliary functions

and

which are the solutions of the following problems:

()

For the problems, we can obtain the following results.

Lemma 6. Let and be the solution of (18) and (19) and , be the solution of (24). Then, we have

()

Proof. Combining (18) and (24), we have

()

By taking

and using Lemma 4, we have

()

where Lemma 4 is used. At last, we can obtain (25) with Cauchy-Schwarz inequality. Equation (26) can be obtained similarly.

The results in [18] can easily be extended to cover the elliptic equations with homogeneous Neumann boundary conditions. Now we list the useful theoretical results in the following lemma.

Lemma 7. Let and be the solution of (4) and (10), respectively, and , be the solution of (24), , f, y_Ω ∈ H¹(Ω), and A ∈ W^2,∞. Then there exists a positive constant C > 0 and h₀ > 0 such that for 0 < h ≤ h₀

()

3.2. L² Error Estimate

Theorem 8. Assume that and are the solutions of (6) and (20), respectively, , f, y_Ω ∈ H¹(Ω), and A ∈ W^2,∞. Then there exists a positive constant C > 0 and h₀ > 0 such that for 0 < h ≤ h₀

()

Proof. Let us test (12) with , and (20) with , and sum up the two inequalities; we have

()

We further get

()

where

()

Combining the above equations, we can obtain

()

According to Lemmas 5, 6, and 7, we have

()

Using Lemmas 5 and 6, we conclude

()

Combining (34)–(37) and using Lemma 7, we can obtain the desirable result

()

Theorem 9. Assume that are the solutions of (6) and (11), respectively, and are the solutions of (18) and (19), respectively, , f, y_Ω ∈ H¹(Ω), and A ∈ W^2,∞. Then there exists a positive constant C > 0 such that

()

Proof. Using the triangle inequality, we have

()

From Lemma 6 and Theorem 8, we can obtain

()

Using Lemma 7, we can obtain the desired result

()

Similarly, we have

()

3.3. H¹ Error Estimate

Theorem 10. Assume that are the solutions of (6) and (11), respectively, and are the solutions of (18) and (19), respectively, , f, y_Ω ∈ L²(Ω), and A ∈ W^1,∞. Then there exists a positive constant C > 0 such that

()

Proof. Using the triangle inequality, we have

()

From Lemma 4, we can obtain

()

By using Lemma 7 and Theorems 8 and 9, we can obtain the desired result

()

Similarly, we have

()

Remark 11. In the case U_ad = L²(Ω), the projection equations (13) and (20) become and , respectively. Using the above theorem, we can obtain the following error estimate:

()

3.4. L^∞ Error Estimate

Theorem 12. Assume that are the solutions of (18), (19), and (20), respectively, , f, y_Ω ∈ H¹(Ω), and A ∈ W^2,∞. Then there exists a positive constant C > 0 such that

()

Proof. Using the projection equations (13) and (20), we have

()

Similarly, we have

()

4. Numerical Experiments

In this section, we report some numerical results of finite volume element schemes for the elliptic optimal control problems. To illustrate the theoretical analysis, the following rate of convergence r is defined:

()

where u_h is the numerical solution with space step size h and u the analytical solution. The rate approaching the number 2 would indicate second-order accuracy in space.

4.1. Experiment 1

To validate the finite volume element schemes for the solution of elliptic optimal control problems, test example is needed for which the exact solutions are known in advance [15]. We consider the problems with homogeneous Neumann boundary condition,

()

subject to

()

where Ω denotes unit square [0,1]×[0,1], U_ad=L²(Ω), n is the outer unit normal vector, and f = 1 − sin²⁡(2πx₁)sin²⁡(2πx₂). Under these settings, the optimal control is

()

The adjoint state is

()

and the associated state is

()

Then we can determine the function y_Ω accordingly.

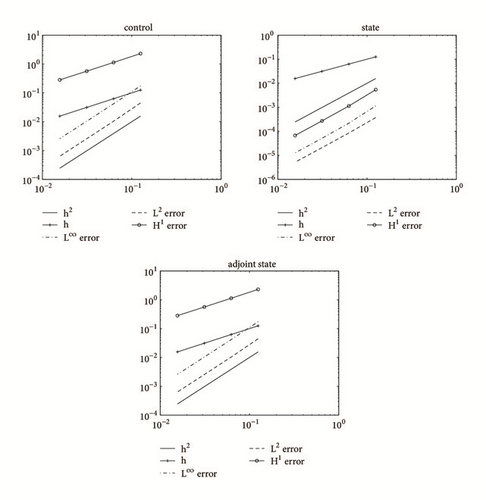
Errors of finite volume element schemes in L^∞, L², and H¹ norm are computed. Data are listed in Tables 1–3. In Tables 1 and 3, errors in H¹ norm have optimal convergence order for both control and adjoint state. These results confirm our theoretical error analysis (44). In Table 2, due to additional smoothness of the state, the H¹ error is O(h²). The convergence results in Tables 1–3 demonstrate second-order accuracy in L^∞ and L² norm for the control, state, and adjoint state.

Table 1. Errors of the control for different error norms.

h	L^∞ error	r	L² error	r	H¹ error	r
1/8	1.7412E-01	-	4.4468E-02	-	2.3006	-
1/16	4.1870E-02	2.05	1.0374E-02	2.09	1.1313	1.02
1/32	1.0476E-02	2.00	2.5558E-03	2.02	5.6371E-01	1.00
1/64	2.6171E-03	2.00	6.3685E-04	2.00	2.8162E-01	1.00

Table 2. Errors of the state for different error norms.

h	L^∞ error	r	L² error	r	H¹ error	r
1/8	1.1429E-03	-	3.7634E-04	-	5.3988E-03	-
1/16	2.1927E-04	2.38	8.5181E-05	2.14	1.1332E-03	2.25
1/32	5.1326E-05	2.09	2.0833E-05	2.03	2.7140E-04	2.06
1/64	1.2609E-05	2.03	5.1751E-06	2.01	6.7061E-05	2.02

Table 3. Errors of the adjoint state for different error norms.

h	L^∞ error	r	L² error	r	H¹ error	r
1/8	1.7415E-02	-	4.4468E-02	-	2.3006	-
1/16	4.1867E-02	2.06	1.0373E-02	2.09	1.1313	1.02
1/32	1.0473E-02	1.99	2.5552E-03	2.02	5.6371E-01	1.00
1/64	2.6159E-03	2.00	6.3655E-04	2.01	2.8162E-01	1.00

Figure 2 depicts the development of the L^∞, L², and H¹ error for the control, state, and adjoint state under uniform refinement of the mesh. From the figure, the expected order O(h²) in L^∞ and L² norm for the control is observed, and the order O(h) in H¹ norm is shown. Additionally, we observe convergence of order O(h²) in L^∞ and L² norm for state and adjoint state. Because of better smoothness of state, the order O(h²) in H¹ norm is also observed.

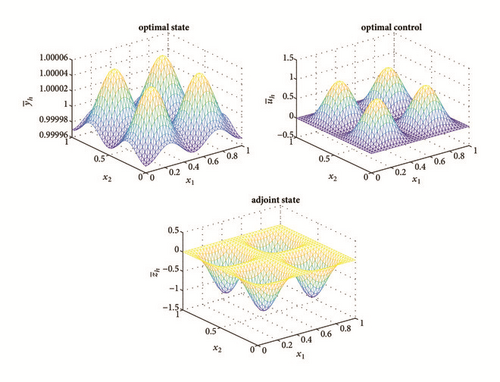
We perform a simulation with space size h = 1/32 for this problem. Figure 3 presents the computed state, optimal control, and adjoint state. Examination of Figure 3 shows that the approximate solutions coincide with the true solutions. At the same time, the relationship between the control and adjoint state is preserved well.

4.2. Experiment 2

Now, we consider the optimal control problem with homogeneous Dirichlet boundary condition and control constraint,

()

subject to

()

where Ω denotes the unit circle, U_ad = {u ∈ L²(Ω):−0.2 ≤ u ≤ 0.2},

, and λ = 0.1.

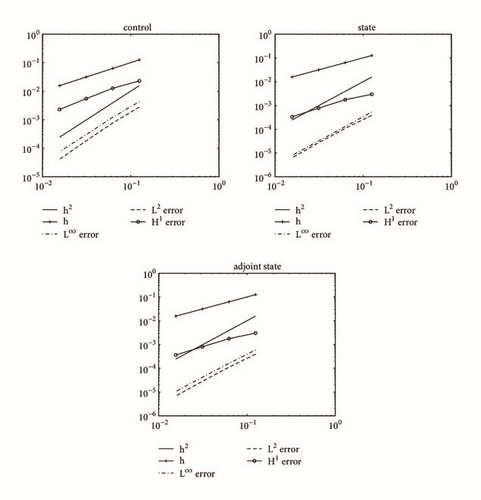
The exact solution of the problem is not known in advance. So we use the numerical results computed on a grid with h = 1/256 as reference solutions. The L^∞, L², and H¹ errors for state, control, and adjoint state of the above problems have been computed. They are displayed in Tables 4–6 for the finite volume element schemes. Examination of the tables shows that the error measures of the schemes diminish approximately quadratically for the error in L^∞ and L² norm and linearly for the error in H¹ norm, which are consistent with our theoretical analysis.

Table 4. Errors of the control for different error norms.

h	L^∞ error	r	L² error	r	H¹ error	r
1/8	4.2814E-03	-	2.7687E-03	-	2.2775E-02	-
1/16	1.2186E-03	1.81	7.7173E-04	1.84	1.2642E-02	0.85
1/32	2.9931E-04	2.02	1.8098E-04	2.09	5.4512E-03	1.21
1/64	7.6218E-05	1.97	4.0938E-05	2.14	2.2949E-03	1.24

Table 5. Errors of the state for different error norms.

h	L^∞ error	r	L² error	r	H¹ error	r
1/8	5.2997E-04	-	3.8069E-04	-	2.9536E-03	-
1/16	1.3047E-04	2.02	1.0869E-04	1.81	1.7383E-03	0.76
1/32	3.2119E-05	2.02	2.7098E-05	2.00	7.6992E-04	1.17
1/64	7.9037E-06	2.02	6.2918E-06	2.10	3.3199E-04	1.21

Table 6. Errors of the adjoint state for different error norms.

h	L^∞ error	r	L² error	r	H¹ error	r
1/8	5.9019E-04	-	3.9236E-04	-	3.0287E-03	-
1/16	1.6144E-04	1.87	1.1101E-04	1.82	1.7719E-03	0.77
1/32	4.2371E-05	1.93	2.8422E-05	1.97	8.0665E-04	1.13
1/64	1.0588E-05	2.00	6.9125E-06	2.04	3.6516E-04	1.14

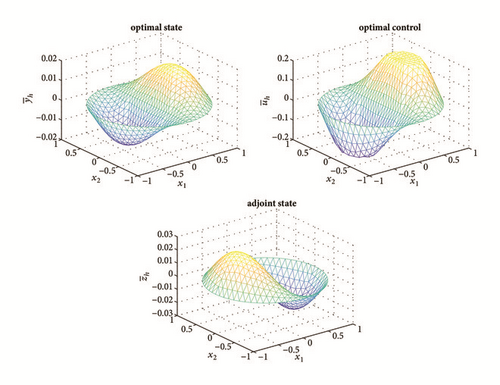
In Figure 4, the development of the L^∞, L², and H¹ error for control, state, and adjoint state under uniform refinement of the mesh is shown. Here, the expected order O(h²) in L^∞ and L² norm for the control is observed. Again, we observe convergence of order O(h²) in L^∞ and L² norm for state and adjoint state, which is consistent with our expectation of the order of convergence. The errors in H¹ norm confirm our error estimation (11). Figure 5 displays the numerical solution computed by the finite volume element schemes with h = 1/16. The results are nearly the same as those in [19]. The relationship between the control and adjoint state is also preserved well.

4.3. Experiment 3

Now we consider the optimal control problem (59) with Ω = (−1,1) ²∖([−1,0]×[0,1]) denoting an L-shaped domain, U_ad = {u ∈ L²(Ω):−0.2 ≤ u ≤ 0.2}. Further, we set and λ = 0.1.

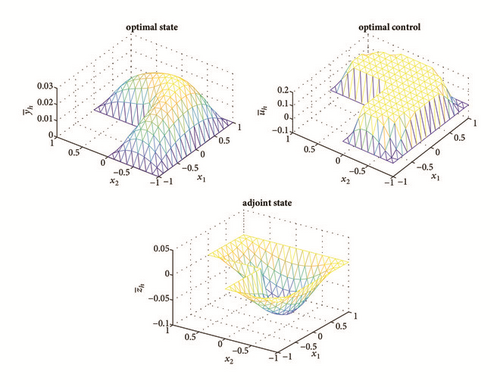
In this situation, the solution does not admit integrable second derivatives. The desired convergence results of finite volume element schemes cannot be expected. So we only present the numerical solutions of the finite volume element schemes in Figure 6, which are nearly the same as those in [19]. On one hand, the desired convergence results may be obtained by using graded meshes and postprocessing [20], which will need more computational cost. On the other hand, we can modify finite volume element schemes near the corner to obtain the second-order accuracy. The related results will be reported in the future.

5. Conclusions

In this article, we have investigated the finite volume element discretizations of optimal control problems governed by linear elliptic partial differential equations and subject to pointwise control constraints. Optimal order L², H¹, and L^∞ error estimates for the considered problems are obtained and numerical experiments validate the theoretical results. In addition, we discuss the optimal control problems in polygonal domains with corner singularities. Two effective methods are proposed to compensate the negative effects of the corner singularities. The corresponding results will be reported in the future.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This project is partially supported by the Fundamental Research Funds for the Central Universities (Nos. KYZ201565 and KJQN201839) and the National Natural Science Foundation of China (Nos. 11701283, 11426134, and 11471166).

Open Research

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Becker R., Kapp H., and Rannacher R., Adaptive finite element methods for optimal control of partial differential equations: basic concept, SIAM Journal on Control and Optimization. (2000) 39, no. 1, 113–132, https://doi.org/10.1137/S0363012999351097, MR1780911, Zbl0967.65080, 2-s2.0-0034461033.
10.1137/S0363012999351097
Web of Science® Google Scholar
2 Arada N., Casas E., and Tröltzsch F., Error estimates for the numerical approximation of a semilinear elliptic control problem, Computational Optimization and Applications. (2002) 23, no. 2, 201–229, https://doi.org/10.1023/A:1020576801966, MR1937089, Zbl1033.65044, 2-s2.0-0036853826.
10.1023/A:1020576801966
Web of Science® Google Scholar
3 Chen Y. and Liu W., Error estimates and superconvergence of mixed finite element for quadratic optimal control, International Journal of Numerical Analysis & Modeling. (2006) 3, no. 3, 311–321, MR2237885, Zbl1125.49026.
Web of Science® Google Scholar
4 Kröner A. and Vexler B., A priori error estimates for elliptic optimal control problems with a bilinear state equation, Journal of Computational and Applied Mathematics. (2009) 230, no. 2, 781–802, https://doi.org/10.1016/j.cam.2009.01.023, MR2536007.
10.1016/j.cam.2009.01.023
Web of Science® Google Scholar
5 Hou T. and Li L., Error estimates of mixed methods for optimal control problems governed by general elliptic equations, Advances in Applied Mathematics and Mechanics. (2016) 8, no. 6, 1050–1071, https://doi.org/10.4208/aamm.2014.m807, MR3572717, 2-s2.0-84988591461.
10.4208/aamm.2014.m807
Web of Science® Google Scholar
6 Zhang Z., Error estimates for finite volume element method for the pollution in groundwater flow, Numerical Methods for Partial Differential Equations. (2009) 25, no. 2, 259–274, https://doi.org/10.1002/num.20340, MR2483766, Zbl1157.76030.
10.1002/num.20340
CAS Web of Science® Google Scholar
7 Wang Q., Zhang Z., and Li Z., A Fourier finite volume element method for solving two-dimensional quasi-geostrophic equations on a sphere, Applied Numerical Mathematics. (2013) 71, 1–13, https://doi.org/10.1016/j.apnum.2013.03.007, MR3064633, Zbl1284.65175.
10.1002/fld.3639
Web of Science® Google Scholar
8 Wang Q., Lin S., and Zhang Z., Numerical methods for a fluid mixture model, International Journal for Numerical Methods in Fluids. (2013) 71, no. 1, 1–12, https://doi.org/10.1002/fld.3639, MR3001212, 2-s2.0-84872376613.
10.1002/fld.3639
Web of Science® Google Scholar
9 Wang Q., Zhang Z., Zhang X., and Zhu Q., Energy-preserving finite volume element method for the improved Boussinesq equation, Journal of Computational Physics. (2014) 270, 58–69, https://doi.org/10.1016/j.jcp.2014.03.053, MR3209375, Zbl1349.76405, 2-s2.0-84898630551.
10.1016/j.jcp.2014.03.053
Web of Science® Google Scholar
10 Ruiz-Baier R. and Torres H., Numerical solution of a multidimensional sedimentation problem using finite volume-element methods, Applied Numerical Mathematics. (2015) 95, 280–291, https://doi.org/10.1016/j.apnum.2013.12.006, MR3349700, Zbl1320.76085.
10.1016/j.apnum.2013.12.006
Web of Science® Google Scholar
11 Chen C. and Liu W., A two-grid finite volume element method for a nonlinear parabolic problem, International Journal of Numerical Analysis & Modeling. (2015) 12, no. 2, 197–210, MR3352447, Zbl1329.65220, 2-s2.0-84929417809.
Web of Science® Google Scholar
12 Bi C. and Wang C., A posteriori error estimates of finite volume element method for second-order quasilinear elliptic problems, International Journal of Numerical Analysis & Modeling. (2016) 13, no. 1, 22–40, MR3421764, Zbl1347.65165, 2-s2.0-84945935128.
Web of Science® Google Scholar
13 Luo X., Chen Y., and Huang Y., Some error estimates of finite volume element approximation for elliptic optimal control problems, International Journal of Numerical Analysis & Modeling. (2013) 10, no. 3, 697–711, MR3064274, Zbl1288.65095, 2-s2.0-84878791836.
Web of Science® Google Scholar
14 Sandilya R. and Kumar S., Convergence analysis of discontinuous finite volume methods for elliptic optimal control problems, International Journal of Computational Methods. (2016) 13, no. 2, 1640012, 20, https://doi.org/10.1142/S0219876216400120, MR3479433, Zbl1359.49008.
10.1142/S0219876216400120
Web of Science® Google Scholar
15 Tröltzsch F., Optimal Control of Partial Differential Equations: Theory, Methods and Applications, 2010, 112, American Mathematical Society.
10.1090/gsm/112
Google Scholar
16 Li R., Chen Z., and Wu W., Generalized difference methods for differential equations, 2000, 226, Marcel Dekker, Inc., Monographs and Textbooks in Pure and Applied Mathematics, MR1731376.
10.1201/9781482270211
Google Scholar
17 Chou S. and Li Q., Error estimates in L²,H¹ and L^∞ in covolume methods for elliptic and parabolic problems: a unified approach, Mathematics of Computation. (2000) 69, no. 229, 103–120, https://doi.org/10.1090/S0025-5718-99-01192-8, MR1680859.
10.1090/S0025-5718-99-01192-8
Web of Science® Google Scholar
18 Ewing R. E., Lin T., and Lin Y., On the accuracy of the finite volume element method based on piecewise linear polynomials, SIAM Journal on Numerical Analysis. (2002) 39, no. 6, 1865–1888, https://doi.org/10.1137/S0036142900368873, MR1897941, Zbl1036.65084, 2-s2.0-0036556364.
10.1137/S0036142900368873
Web of Science® Google Scholar
19 Hinze M., Pinnau R., Ulbrich M., and Ulbrich S., Optimization with PDE Constraints, 2009, Springer, MR2516528, Zbl1167.49001.
Google Scholar
20 Apel T., Rösch A., and Sirch D., L^∞ error estimates on graded meshes with application to optimal control, SIAM Journal on Control and Optimization. (2009) 48, no. 3, 1771–1796, https://doi.org/10.1137/080731724, MR2516188.
10.1137/080731724
Web of Science® Google Scholar

Citing Literature

All articles

Finite Volume Element Approximation for the Elliptic Equation with Distributed Control

Abstract

1. Introduction