In this paper we consider a numerical method for solving nonhomogeneous backward heat conduction problem. Coupled with the likewise Crank Nicolson scheme and an intermediate variable, the backward problem is transformed to a nonhomogeneous Helmholtz type problem; the unknown initial temperature can be obtained by solving this Helmholtz type problem. To illustrate the effectiveness and accuracy of the proposed method, we solve several problems in both two and three dimensions. The results show that this numerical method can solve nonhomogeneous backward heat conduction problem effectively and precisely, even though the final temperature is disturbed by significant noise.

1. Introduction

The heat conduction equation is a kind of very important time-dependent parabolic partial differential equation; it describes the distribution of heat or temperature in a given region over time and is widely used in diverse scientific fields, such as the study of Brownian motion [1], to solve the Black-Scholes partial differential equation [2] and the research of chemical diffusion. Many works have been done to study the heat conduction problem [3–5]. The purpose of this article is to numerically solve nonhomogeneous backward heat conduction problem. This problem is one kind of inverse problem, also called final value problem or time inverse problem.

In many engineering and application areas we need to reconstruct the unknown initial heat energy or temperature from the final measured one; it is a typical inverse problem which is related to the initial boundary value problems in heat conduction. As we all know, there are many kinds of inverse problems in mathematical physics, such as boundary inverse problems [6, 7], coefficient inverse problems [8, 9], and evolutionary inverse problems (or time inverse problem) [10, 11]. The backward heat conduction problem is a time inverse problem, in which the initial conditions are unknown; instead the final data are observable.

In the sense of Hadamard [12], the inverse problem is always considered as a class of classically ill-posed problem, which means that a small error in the input data may cause enormous error to the result. The backward heat conduction problem is a typically ill-posed problem, because of the measurement error of the input data. Most standard numerical method can not achieve a good result in solving an ill-posed problem, due to the ill-posedness of the problem and the ill-conditioning of the discretized matrix, so, it is very important to find a stable and efficient numerical algorithm to solve ill-posed problems.

The backward heat conduction problem arises in many physical and chemical fields and has attracted the attention of many researchers. The improperly posed backward heat conduction problem has been considered by L. Payne [13], and Miranker [14] has given a research of the uniqueness conditions for the backward heat conduction problem. There are also many works that have been done to numerically solve the ill-posed backward heat conduction problem. In [15], Fourier regularization method is used to solve one-dimensional backward heat problem, H. Han [16] has considered this problem using boundary element method, and also some other numerical methods for solving backward heat conduction problem have been given in many works, such as finite difference method [17, 18], iterative boundary element method [19, 20], the method of fundamental solution [21], etc. Most of these methods are used to solve one-dimensional homogeneous situations; there are a few papers on the nonhomogeneous case in higher dimensional space. Scientists M. Denche and A. Abdessemed [22] gave extensions of the quasi-boundary methods to the nonhomogeneous case. Paper [23] regularized the two-dimensional nonhomogeneous backward heat problem by perturbing the final value. M. Li, T. S. Jiang, and Y. C. Hon have solved nonhomogeneous situations by using a new meshless method based on radial basis functions [11].

In this paper we consider the nonhomogeneous backward heat conduction problem in two- or three-dimensional spatial domains. We propose a new numerical method to solve this severely ill-posed problem; coupled with the likewise Crank-Nicolson scheme and a new variable, the backward problem is transformed to a nonhomogeneous Helmholtz type problem; by solving this nonhomogeneous Helmholtz type problem and submitting back to the new variable, we can get the solution of the initial condition.

The structure of the paper is organized as follows: In Section 2, we briefly introduce the formulation of the nonhomogeneous backward heat conduction problem. In Section 3, we introduce the numerical method and apply this method on the inverse problem. The results of several two- and three-dimensional numerical experiments are presented to illustrate the stability and accuracy of the proposed method in Section 4. Section 5 is dedicated to a brief conclusion. Finally, some references are introduced at the end.

2. The Formulation of the Problem

We consider the nonhomogeneous backward heat conduction problem in a bounded and connected domain

with the boundary Γ = ∂Ω in the following,

(1)

with the final temperature condition,

(2)

and the Dirichlet boundary conditions,

(3)

where f(x, t), g(x), and h(x, t) are known functions, Δ is Laplace Operator, and u(x, t) satisfies the nonhomogeneous heat conduction equation (1). The problem which we want to solve in this paper is the backward heat conduction problem; we will determine the temperature before some particular time T from the known data (2) at time T and the boundary conditions (3).

3. The Computational Algorithm

To solve the backward problem (1)–(3) numerically, we introduce the grid of time,

(4)

Using the notation uⁿ(x) = u(x, tⁿ) and a similar format as Crank-Nicolson (C-N) scheme to approximate the heat equation (1) with second order at the time moment t^n+1/2 = (tⁿ⁺¹ + tⁿ)/2, we have

(5)

where n = 0,1, …, N − 1. Here, it is worth mentioning that in (5) we did not use the C-N approximation scheme, but a scheme has a similar format as C-N scheme, which we called the likewise C-N scheme [24].

By using a new intermediate variable

, which is given as follows,

(6)

(5) can be transformed in the following new form,

(7)

By simplifying (7), we can get

(8)

Notice that (8) is a nonhomogeneous Helmholtz equation with

as solution; it can be written as

(9)

where

(10)

with the boundary conditions,

(11)

where hⁿ(x) = h(x, tⁿ) is known from the Dirichlet boundary conditions (3).

To get the solution

from the nonhomogeneous Helmholtz equation (9) with boundary conditions (11), the finite element method is used. We multiply by a test function v, which vanishes on the boundary, and apply integration by parts, getting the variational problem with n = 0,1, …, N − 1 as follows,

(12)

where k², F(x, t) are given in (10). We can obtain the value of

by solving the nonhomogeneous Helmholtz equation (8) (or (9)); then, the solution uⁿ can be computed from (6). After repeating the above steps N times, we can get the initial temperature at n = 0.

The Helmholtz equation often appears in the study of physical problems; it is caused by the propagation of time harmonics and applied in many science and engineering fields, such as acoustic, electromagnetic science, and geophysical problems. Many experts have studied solving Helmholtz equation by finite element method (FEM); F. Ihlenburg and I. Babuka studied the finite element solution of the Helmholtz equation with high wave number by using the h-version [25] and h-p version [26] of the FEM. The Least-Squares stabilization of finite element computation for the Helmholtz equation is considered by I. Harari and F. Magoulès [27]. Y. Wong and G. Li [28] consider a new finite difference scheme for solving the Helmholtz equation at any wavenumber, etc.

From [25–28] and the references it can be found that, due to the so-called pollution effect [29], to compute approximate solutions of the Helmholtz equation for high wave numbers by the standard finite element method (FEM) is unreliable, so, in (9), the wave number should be not high. Suppose the numerical discrete grid size is h; in order to ensure an accurate numerical solution, the condition k²h < 1 must be enforced and it is necessary to require kh to be small. A conclusion that the stability constant does not depend on k if k²h is bounded using FEM to solve the Helmholtz equation was given in [25, 26]. Also, a convergence theorem is stated in [30] under the assumption that k²h is sufficiently small. As a result of the fact that the wave number k in the Helmholtz equation (9) is related to the time step τ, in order to ensure stability and accuracy, the time step τ should be selected carefully; it can not be chosen too small.

4. Numerical Examples

In this section we give several numerical examples in both 2D and 3D to demonstrate the effectiveness and stability of the new computation method. In the computation, we impose the noise to the final temperature condition. We set

(13)

where g(x) denotes the exact final temperature condition, δ is the tolerated noise level, and rand n is Gaussian random number with mean 0 and variance 1.

Two kinds of errors are used to compare the accuracy of the numerical solutions with the exact solutions. The maximum error (Maxerror) and the root-mean-square error (RMSE) are defined as follows,

(14)

where M is the total number of testing nodes within the domain and

denotes the approximate solution at the ith node; u_i is the exact one.

Example 1. In this example we consider the two-dimensional nonhomogeneous heat conduction equation (1), with the Dirichlet boundary conditions,

(15)

the final conditions,

(16)

and f(x, t) = π²(ysin⁡(πx) + xcos⁡(πy))cos⁡t − (ysin⁡(πx) + xcos⁡(πy))sin⁡t.

The computational domain is a given rectangle in space such that and , using the map

(17)

to take a point in the rectangular

geometry and to map it to a point (x, y) in a big hollow cylinder.

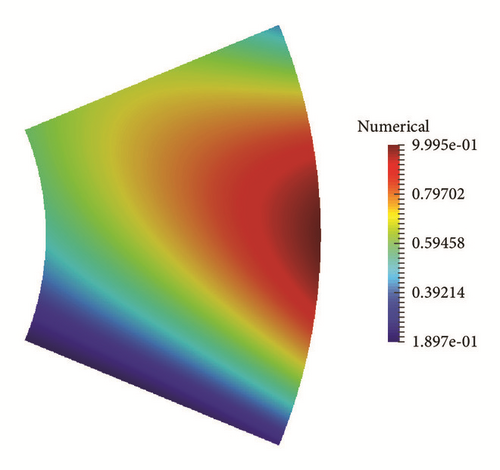
In the computation we choose the mesh 41 × 81 on the rectangular and using the same map to put the mesh on the hollow cylinder, the mesh on the computational domain with a = c = 0.5, b = 1.0, d = 1.5, and θ = π/2 is shown in Figure 1.

The Maxerror and RMSE for T = 1.0, 2.0, and 3.0 are shown in Table 1 with noise level δ = 10⁻³ and various time steps τ. It can be seen from Table 1 that the proposed method performs well for solving the backward problem.

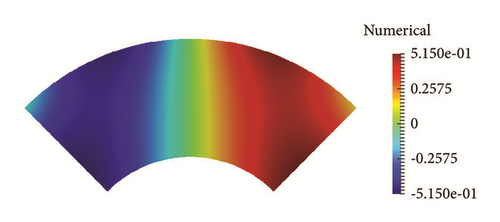
The figure of numerical initial solutions with T = 1.0, τ = 0.25, and δ = 10⁻³ is presented in Figure 2.

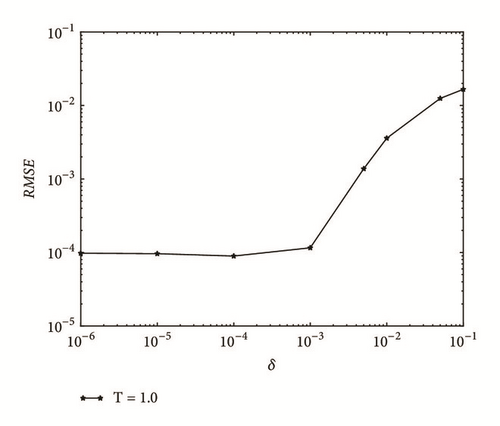
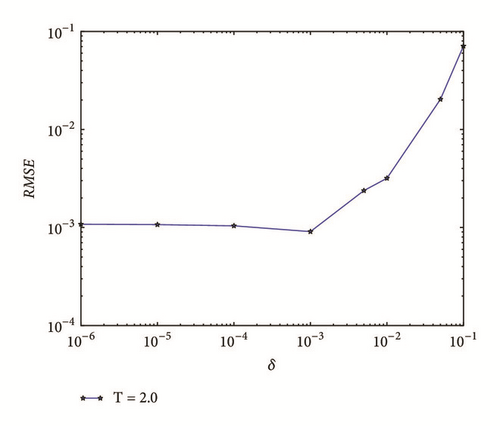
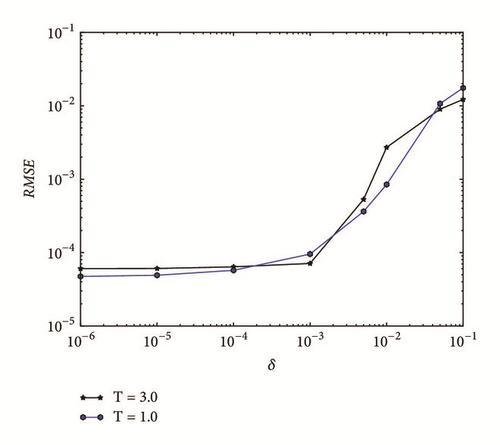
For further investigations, we give a research of the results with a disturbed δ of the final time conditions; the figure of RMSE with different noisy level δ with τ = 0.25 is present in Figures 3 and 4 for T = 1.0 and T = 2.0, respectively.

We also discuss the results under different grids; the Maxerror and RMSE for T = 1.0,2.0 and 3.0 are shown in Table 2 with various grids with noise level δ = 10⁻³ and time steps τ = 0.25.

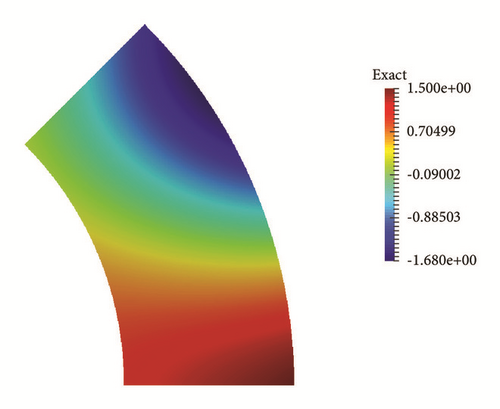
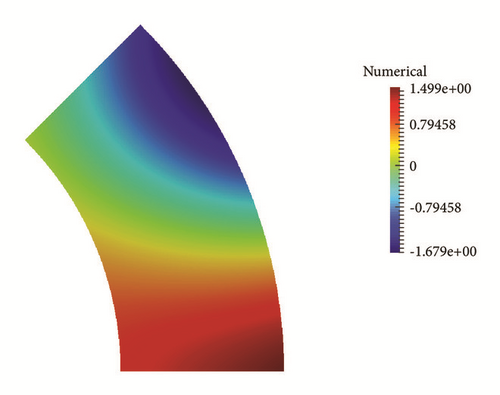
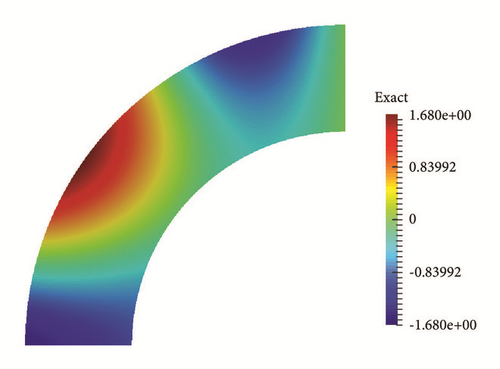
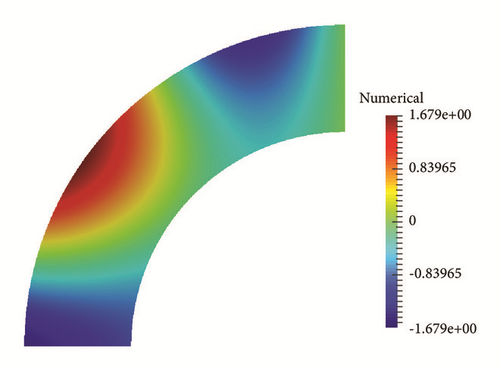
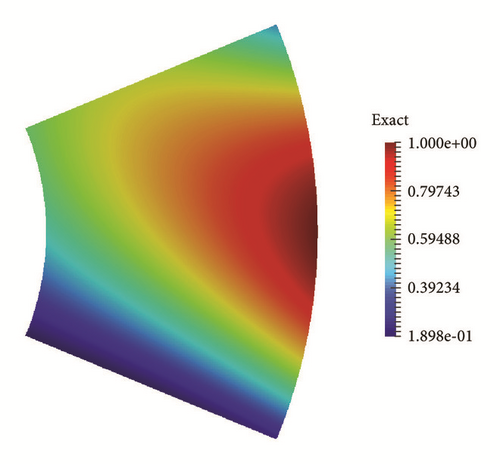
To illustrate the generality, we choose different variables for the computational domain. The figures of the exact and numerical initial solutions are given in Figures 5–7 with different variables of the computational domain. In this computation we choose the mesh 81 × 161, τ = 0.2 and δ = 10⁻³, T = 1.

Table 1. Maxerror and RMSE for T = 1.0,2.0 and 3.0 with different τ.

	τ = 0.2	τ = 0.25	τ = 0.5	τ = 1.0
T = 1.0
Maxerror	4.951 × 10⁻⁴	3.714 × 10⁻⁴	8.721 × 10⁻⁴	1.635 × 10⁻²
RMSE	2.230 × 10⁻⁴	2.358 × 10⁻⁴	4.734 × 10⁻⁴	8.604 × 10⁻³

T = 2.0
Maxerror	2.393 × 10⁻³	2.041 × 10⁻³	4.100 × 10⁻³	1.569 × 10⁻²
RMSE	1.172 × 10⁻³	1.016 × 10⁻³	2.133 × 10⁻³	8.278 × 10⁻³

T = 3.0
Maxerror	2.336 × 10⁻³	1.620 × 10⁻³	6.557 × 10⁻³	3.554 × 10⁻³
RMSE	1.046 × 10⁻³	1.766 × 10⁻³	3.320 × 10⁻³	8.416 × 10⁻⁴

Table 2. Maxerror and RMSE for T = 1.0,2.0,3.0 with different grids.

	21 × 41	41 × 81	81 × 161	161 × 321
T = 1.0
Maxerror	3.256 × 10⁻⁴	2.205 × 10⁻⁴	1.466 × 10⁻⁴	3.418 × 10⁻⁴
RMSE	6.786 × 10⁻⁵	1.358 × 10⁻⁴	8.334 × 10⁻⁵	2.276 × 10⁻⁴

T = 2.0
Maxerror	1.362 × 10⁻³	1.665 × 10⁻³	2.013 × 10⁻³	1.982 × 10⁻³
RMSE	2.888 × 10⁻⁴	8.172 × 10⁻⁴	1.020 × 10⁻³	1.009 × 10⁻³

T = 3.0
Maxerror	2.061 × 10⁻³	5.661 × 10⁻³	3.301 × 10⁻³	7.441 × 10⁻³
RMSE	5.832 × 10⁻⁴	2.751 × 10⁻³	1.565 × 10⁻³	3.705 × 10⁻³

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The domain with computational grid.

Example 2. We also consider the 2D nonhomogeneous backward heat conduction problem in this example; the known conditions are presented as follows,

(18)

and f(x, t) = (π²y² + π²x² − 1)sin⁡(πxy)exp⁡(−t).

In this example, the calculation area is a square of the center at origin; side length is 1. In the computation using the mesh 51 × 51, the computational grid is shown in Figure 8. The Maxerror and RMSE for T = 1.0,2.0,3.0 are shown in Table 3 with δ = 10⁻³ and various τ.

The errors of RMSE with different δ are also given in Figure 9. In this figure τ = 0.2, and the mesh is the same as Figure 8.

The same with Example 1, we also consider the results with different meshes; the Maxerror and RMSE for T = 1.0,2.0 and 3.0 are shown in Table 4 with various meshes with noise level δ = 10⁻³ and time steps τ = 0.2.

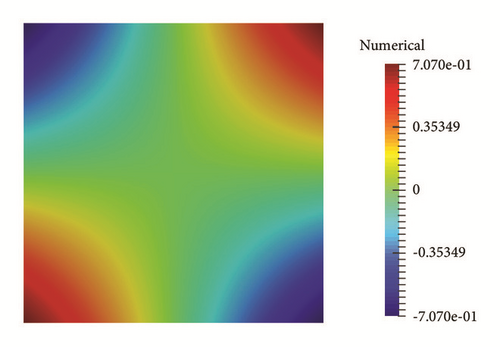
The figure of numerical solutions u(x, y, 0) with T = 1, τ = 0.2, and δ = 10⁻³ is presented in Figure 10; the computational mesh is 51 × 51.

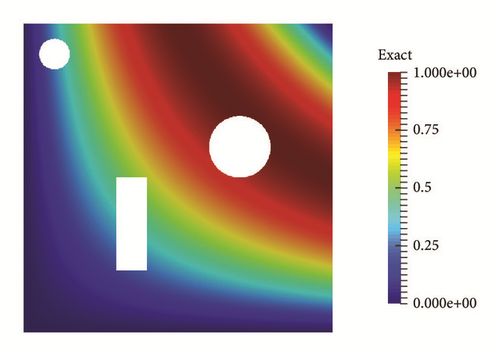
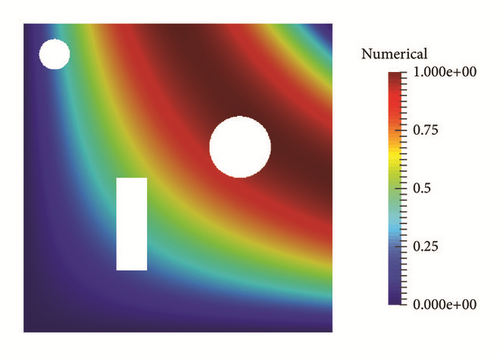
We also consider a slightly more complicated computational area, one unit square to remove a small rectangle and two small circles. In this case, the computation is a little more complicated; we define the unite square as and the small rectangle as Ω₂,

(19)

the two small circles as

(20)

and the computational domain is defined as

(21)

The figure of the domain with the computational mesh can be seen in Figure 11 and the figure of solutions u(x, y, 0) ia also given in Figure 12 with T = 3, τ = 0.2.

Table 3. Maxerror and RMSE for T = 1,2, 3 with different τ.

	τ = 1.0	τ = 0.5	τ = 0.25	τ = 0.2
T = 1.0
Maxerror	1.301 × 10⁻³	1.374 × 10⁻⁴	2.504 × 10⁻⁴	4.221 × 10⁻⁴
RMSE	5.907 × 10⁻⁴	5.727 × 10⁻⁵	1.409 × 10⁻⁴	2.280 × 10⁻⁴

T = 2.0
Maxerror	7.725 × 10⁻⁴	1.513 × 10⁻⁴	6.912 × 10⁻⁵	2.041 × 10⁻⁴
RMSE	3.463 × 10⁻⁴	6.095 × 10⁻⁵	3.407 × 10⁻⁵	1.015 × 10⁻⁴

T = 3.0
Maxerror	9.877 × 10⁻⁴	2.187 × 10⁻⁴	6.443 × 10⁻⁵	4.832 × 10⁻⁴
RMSE	4.474 × 10⁻⁴	9.301 × 10⁻⁵	1.911 × 10⁻⁵	2.457 × 10⁻⁴

Table 4. Maxerror and RMSE for T = 1.0,2.0,3.0 with different grids.

	21 × 21	51 × 51	101 × 101	201 × 201
T = 1.0
Maxerror	4.767 × 10⁻⁴	4.114 × 10⁻⁴	9.978 × 10⁻⁵	1.744 × 10⁻⁴
RMSE	1.409 × 10⁻⁴	2.221 × 10⁻⁴	4.938 × 10⁻⁵	9.225 × 10⁻⁵

T = 2.0
Maxerror	2.644 × 10⁻⁴	2.124 × 10⁻⁴	3.899 × 10⁻⁴	3.138 × 10⁻⁴
RMSE	4.982 × 10⁻⁵	1.058 × 10⁻⁴	1.986 × 10⁻⁴	1.621 × 10⁻⁴

T = 3.0
Maxerror	5.485 × 10⁻⁴	4.497 × 10⁻⁴	5.738 × 10⁻⁴	6.567 × 10⁻⁴
RMSE	2.807 × 10⁻⁴	2.288 × 10⁻⁴	2.925 × 10⁻⁴	3.353 × 10⁻⁴

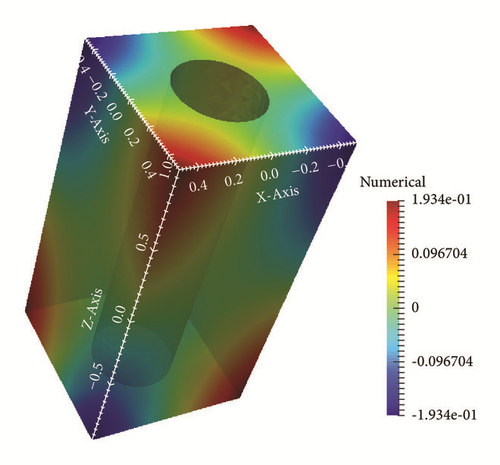
Example 3. In this example we consider the inverse problem in three dimensions with the Dirichlet boundary conditions,

(22)

the final conditions,

(23)

and f(x, t) = sin⁡xsin⁡ysin⁡z(3cos⁡t − sin⁡t); the analytical solution is

(24)

In this example we choose the 3D computational domain defined as a cube without a cylinder insider. The cube is defined as

(25)

the cylinder is defined as

(26)

and the computational domain is

. The domain with the computational grid is shown in Figure 13.

The Maxerror and RMSE for T = 1.0,3.0,5.0 are shown in Table 5 with noise level δ = 10⁻³ and various τ.

The figure of numerical initial solutions with T = 1, τ = 0.2 with noisy level δ = 10⁻³ can be seen in Figure 14.

Table 5. Maxerror and RMSE for T = 1,3, 5 with different τ.

	τ = 1/2	τ = 1/3	τ = 1/4	τ = 1/5
T = 1.0
Maxerror	4.726 × 10⁻⁴	2.014 × 10⁻³	4.399 × 10⁻⁴	1.409 × 10⁻³
RMSE	5.653 × 10⁻⁵	1.499 × 10⁻⁴	4.827 × 10⁻⁵	1.489 × 10⁻⁴

T = 3.0
Maxerror	1.807 × 10⁻³	1.161 × 10⁻⁴	1.717 × 10⁻³	2.961 × 10⁻⁴
RMSE	1.983 × 10⁻⁴	3.789 × 10⁻⁵	1.974 × 10⁻⁴	6.815 × 10⁻⁵

T = 5.0
Maxerror	6.437 × 10⁻⁴	1.125 × 10⁻³	6.596 × 10⁻⁴	1.206 × 10⁻³
RMSE	6.681 × 10⁻⁵	1.225 × 10⁻⁴	7.013 × 10⁻⁵	1.629 × 10⁻⁴

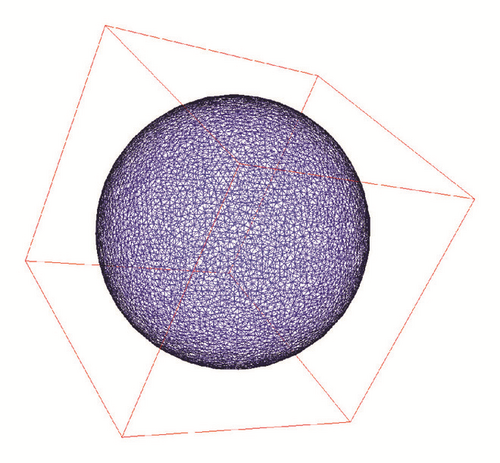
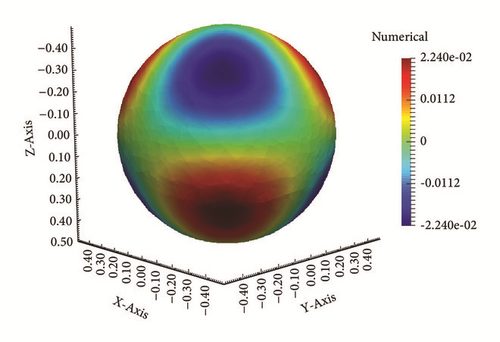
Example 4. In this example we also consider the inverse problem with the same conditions in Example 3, but the computational domain is a sphere with the center at origin and the diameter is 1. The domain with the computational grid is shown in Figure 15.

The Maxerror and RMSE for T = 1.0,2.0,3.0 are shown in Table 6 with noise level δ = 10⁻³ and various τ.

The figure of numerical initial solutions with T = 3, τ = 0.2 with noisy level δ = 10⁻³ can be seen in Figure 16.

Table 6. Maxerror and RMSE for T = 1,2, 3 with different τ.

	τ = 1/2	τ = 1/3	τ = 1/4	τ = 1/5
T = 1.0
Maxerror	3.765 × 10⁻⁵	1.119 × 10⁻⁴	3.521 × 10⁻⁵	1.119 × 10⁻⁴
RMSE	7.204 × 10⁻⁶	1.780 × 10⁻⁵	6.112 × 10⁻⁶	1.766 × 10⁻⁵

T = 2.0
Maxerror	1.021 × 10⁻⁴	1.028 × 10⁻⁴	1.025 × 10⁻⁴	1.031 × 10⁻⁴
RMSE	1.742 × 10⁻⁵	1.645 × 10⁻⁵	1.658 × 10⁻⁵	1.638 × 10⁻⁵

T = 3.0
Maxerror	1.431 × 10⁻⁴	1.364 × 10⁻⁵	1.463 × 10⁻⁴	3.104 × 10⁻⁴
RMSE	2.497 × 10⁻⁵	3.921 × 10⁻⁶	2.324 × 10⁻⁵	1.172 × 10⁻⁵

5. Conclusion

In this paper, we proposed a new numerical scheme to solve nonhomogeneous backward heat conduction problem with two- and three-dimensional computational domain. In our method, using likewise Crank Nicolson scheme and introducing a new intermediate variable, transforming the backward problem to a nonhomogeneous Helmholtz problem, and solving the Helmholtz problem using finite element method, we get the initial temperature. This new method is easy to calculate and from the numerical results presented in the previous it can be seen that this new method is effective for solving such problems.

It is worth to note that, due to the limitations of the standard finite element method in solving Helmholtz equations with high wave numbers, to solve the Helmholtz problem (9) by FEM, the time step τ should be carefully chosen, in order to ensure the wave number in (9) is not high, and for high dimension problem, dense grids need to be generated to ensure accuracy, resulting in increased computational time. Many works have been done in solving Helmholtz problem with high wave numbers [25–28]; these methods can be used instead of the standard FEM to solve the Helmholtz problem (9), so that these problems will be somewhat improved.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

The authors would like to to thank professors P. N. Vabishchevish and V. I. Vasilév for their important guidance and advice in the paper writing. This work is supported by RFBR (project 17-01-00732).

Open Research

Data Availability

All the data used to support the findings of this study are included within the article.

References

1 Fan J. and Wang L., Review of heat conduction in nanofluids, Journal of Heat Transfer. (2011) 133, no. 4, 801–815, https://doi.org/10.1115/1.4002633.
10.1115/1.4002633
Web of Science® Google Scholar
2 Paliathanasis A., Morris R. M., and Leach P. G. L., Lie symmetries of (1+2) nonautonomous evolution equations in financial mathematics, Mathematics. (2016) 4, no. 2, 1–14.
10.3390/math4020034
Web of Science® Google Scholar
3 Bartoshevich M. A., A heat-conduction problem, Journal of Engineering Physics. (1975) 28, no. 2, 240–244, 2-s2.0-0016471610, https://doi.org/10.1007/BF00865850.
10.1007/BF00865850
Google Scholar
4 Alifanov O. M., Inverse Heat Transfer Problems, 1994, Springer-Verlag, International Series in Heat and Mass Transfer.
10.1007/978-3-642-76436-3
Google Scholar
5 Huang C.-H. and Wang S.-P., A three-dimensional inverse heat conduction problem in estimating surface heat flux by conjugate gradient method, International Journal of Heat and Mass Transfer. (1999) 42, no. 18, 3387–3403, 2-s2.0-0345035216, https://doi.org/10.1016/S0017-9310(99)00020-4, Zbl0977.74594.
10.1016/S0017-9310(99)00020-4
CAS Web of Science® Google Scholar
6 Aparicio N. D. and Pidcock M. K., The boundary inverse problem for the Laplace equation in two dimensions, Inverse Problems. (1996) 12, no. 5, 565–577, https://doi.org/10.1088/0266-5611/12/5/003, MR1413419.
10.1088/0266-5611/12/5/003
Web of Science® Google Scholar
7 Vasilev V. V., Vasilyeva M. V., and Kardashevskyc A. M., The numerical solution of the boundary inverse problem for a parabolic equation, American Institute of Physics. (2016) 1773, no. 1, 100010(1)–100010(7).
Google Scholar
8 Su L., Vabishchevish P. N., and Vasil′ev V. I., The inverse problem of the simultaneous determination of the right-hand side and the lowest coefficients in parabolic equations, Numerical Analysis and Its Applications, 2017, 633–639, Lecture Notes in Computer Science, https://doi.org/10.1007/978-3-319-57099-0_72, MR3661295.
10.1007/978-3-319-57099-0_72
Google Scholar
9 Vabishchevich P. N. and Vasil′ev V. I., Computational algorithms for solving the coefficient inverse problem for parabolic equations, Inverse Problems in Science and Engineering. (2016) 24, no. 1, 42–59, https://doi.org/10.1080/17415977.2014.993984, MR3437392, 2-s2.0-84919935517.
10.1080/17415977.2014.993984
Web of Science® Google Scholar
10 Samarskii A. A. and Vabishchevich P. N., Numerical Methods for Solving Inverse Problems of Mathematical Physics, 2007, Walter de Gruyter, Inverse and Ill-Posed Problems Series, https://doi.org/10.1515/9783110205794, MR2381619.
10.1515/9783110205794
Google Scholar
11 Li M., Jiang T., and Hon Y. C., A meshless method based on RBFs method for nonhomogeneous backward heat conduction problem, Engineering Analysis with Boundary Elements. (2010) 34, no. 9, 785–792, https://doi.org/10.1016/j.enganabound.2010.03.010, MR2658025, Zbl1244.80023, 2-s2.0-79951514568.
10.1016/j.enganabound.2010.03.010
Web of Science® Google Scholar
12 Hadamard J., Lectures on Cauchy Problems in Linear Partial Differential Equations, 1923, New Haven Yale University Press.
Google Scholar
13 Payne L., Improperly Posed Problems in Partial Differential Equations, 1975, Society for Industrial and Applied Mathematics.
10.1137/1.9781611970463
Google Scholar
14 Miranker W. L., A well posed problem for the backward heat equation, Proceedings of the American Mathematical Society. (1961) 12, no. 2, 243–247, https://doi.org/10.2307/2034314, MR0120462.
10.1090/S0002-9939-1961-0120462-2
Google Scholar
15 Fu C.-L., Xiong X.-T., and Qian Z., Fourier regularization for a backward heat equation, Journal of Mathematical Analysis and Applications. (2007) 331, no. 1, 472–480, https://doi.org/10.1016/j.jmaa.2006.08.040, MR2306017, Zbl1146.35420, 2-s2.0-33947105490.
10.1016/j.jmaa.2006.08.040
Web of Science® Google Scholar
16 Han H., Ingham D. B., and Yuan Y., The boundary element method for the solution of the backward heat conduction equation, Journal of Computational Physics. (1995) 116, no. 2, 292–299, 2-s2.0-0001293247, https://doi.org/10.1006/jcph.1995.1028, Zbl0821.65064.
10.1006/jcph.1995.1028
Web of Science® Google Scholar
17 Iijima K., Numerical solution of backward heat conduction problems by a high order lattice-free finite difference method, Journal of the Chinese Institute of Engineers. (2004) 27, no. 4, 611–620, https://doi.org/10.1080/02533839.2004.9670908.
10.1080/02533839.2004.9670908
Web of Science® Google Scholar
18 Shidfar A. and Zakeri A., A numerical technique for backward inverse heat conduction problems in one-dimensional space, Applied Mathematics and Computation. (2005) 171, no. 2, 1016–1024, https://doi.org/10.1016/j.amc.2005.01.125, MR2199684, 2-s2.0-31144463522.
10.1016/j.amc.2005.01.125
Web of Science® Google Scholar
19 Lesnic D., Elliott L., and Ingham D. B., An iterative boundary element method for solving the backward heat conduction problem using an elliptic approximation, Inverse Problems in Science and Engineering. (1998) 6, no. 4, 255–279, https://doi.org/10.1080/174159798088027679.
10.1080/174159798088027679
CAS Google Scholar
20 Mera N. S., Elliott L., Ingham D. B., and Lesnic D., Iterative boundary element method for solving the one-dimensional backward heat conduction problem, International Journal of Heat and Mass Transfer. (2001) 44, no. 10, 1937–1946, 2-s2.0-0034744604, https://doi.org/10.1016/S0017-9310(00)00235-0.
10.1016/S0017-9310(00)00235-0
Web of Science® Google Scholar
21 Hon Y. C. and Li M., A discrepancy principle for the source points location in using the MFS for solving the BHCP, International Journal of Computational Methods. (2009) 6, no. 2, 181–197, https://doi.org/10.1142/S0219876209001759, MR2542025.
10.1142/S0219876209001759
Web of Science® Google Scholar
22 Denche M. and Abdessemed A., On regularization and error estimates for non-homogeneous backward Cauchy problem, Arab Journal of Mathematical Sciences. (2012) 18, no. 2, 149–164, https://doi.org/10.1016/j.ajmsc.2012.03.002, MR2922676, Zbl1248.35229.
10.1016/j.ajmsc.2012.03.002
Google Scholar
23 Tuan N. H. and Trong D. D., A new regularized method for two dimensional nonhomogeneous backward heat problem, Applied Mathematics and Computation. (2009) 215, no. 3, 873–880, https://doi.org/10.1016/j.amc.2009.06.020, MR2568944, 2-s2.0-69349093113, Zbl1180.65119.
10.1016/j.amc.2009.06.020
Web of Science® Google Scholar
24 Reutskiy S. Y., Chen C. S., and Tian H. Y., A boundary meshless method using Chebyshev interpolation and trigonometric basis function for solving heat conduction problems, International Journal for Numerical Methods in Engineering. (2008) 74, no. 10, 1621–1644, https://doi.org/10.1002/nme.2230, MR2415963, 2-s2.0-47249148497.
10.1002/nme.2230
Web of Science® Google Scholar
25 Ihlenburg F. and Babuška I., Finite element solution of the Helmholtz equation with high wave number Part I: The h-version of the FEM, Computers & Mathematics with Applications. (1995) 30, no. 9, 9–37, https://doi.org/10.1016/0898-1221(95)00144-N.
10.1016/0898-1221(95)00144-N
Web of Science® Google Scholar
26 Ihlenburg F. and Babuka I., Finite element solution of the Helmholtz equation with high wave number part II: the h-p Version of the FEM, SIAM Journal on Numerical Analysis. (1997) 34, no. 1, 315–358.
10.1137/S0036142994272337
Web of Science® Google Scholar
27 Harari I. and Magoulés F., Numerical investigations of stabilized finite element computations for acoustics, Wave Motion. (2004) 39, no. 4, 339–349, https://doi.org/10.1016/j.wavemoti.2003.12.001, MR2058661.
10.1016/j.wavemoti.2003.12.001
Web of Science® Google Scholar
28 Wong Y. S. and Li G., Exact finite difference schemes for solving Helmholtz equation at any wavenumber, International Journal of Numerical Analysis & Modeling- Series B. (2011) 2, no. 1, 91–108, MR2866996, Zbl1272.65083.
Google Scholar
29 Babuka I. and Sauter S. A., Is the pollution effect of the fem avoidable for the Helmholtz equation considering high wave, SIAM Journal on Numerical Analysis. (1997) 34, no. 1, 2392–2423.
10.1137/S0036142994269186
Web of Science® Google Scholar
30 Bayliss A., Goldstein C. I., and Turkel E., On accuracy conditions for the numerical computation of waves, Journal of Computational Physics. (1985) 59, no. 3, 396–404, https://doi.org/10.1016/0021-9991(85)90119-6, MR794614, 2-s2.0-0000350889.
10.1016/0021-9991(85)90119-6
Web of Science® Google Scholar

Citing Literature

All articles

Numerical Method for Solving Nonhomogeneous Backward Heat Conduction Problem

Abstract

1. Introduction

2. The Formulation of the Problem

3. The Computational Algorithm

4. Numerical Examples

5. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Numerical Method for Solving Nonhomogeneous Backward Heat Conduction Problem

Abstract

1. Introduction

2. The Formulation of the Problem

3. The Computational Algorithm

4. Numerical Examples

5. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information