We give a scheme of approximation of the MK problem based on the symmetries of the underlying spaces. We take a Haar type MRA constructed according to the geometry of our spaces. Thus, applying the Haar type MRA based on symmetries to the MK problem, we obtain a sequence of transportation problem that approximates the original MK problem for each of MRA. Moreover, the optimal solutions of each level solution converge in the weak sense to the optimal solution of original problem.

1. Introduction

The optimal transport problem was first formulated by Monge in 1781 and concerned finding the optimal way in the sense of minimal transportation cost of moving a pile of soil from one site to another. This problem was given a modern formulation in the work of Kantorovich in 1942 and so is now known as the Monge-Kantorovich problem.

On the other hand, a big advantage over schemes of approximation was given in the seminal article [1]; it introduced approximation schemes for infinite linear program; in particular, it showed that under suitable assumptions the program’s optimum value can be finite-dimensional linear programs and that, in addition, every accumulation point of a sequence of optimal solutions for the approximating programs is an optimal solution for the original problem. An example given in this article is the Monge-Kantorovich mass transfer (MK) problem on the space itself, where the underlying space is compact.

In [2], a general method of approximation for the MK problem is given, where X and Y are Polish spaces; however, this method is noneasier implementation. Later, in [3], a scheme of approximation of MK problem is provided, which consists in giving a sequence of finite transportation problems underlying original MK problem (the space is compact); nevertheless, a general procedure is given, but the examples are in a two-dimensional cube and use the dyadic partition of the cube for approximation. Our objective is to give other families to approximate this kind of problems, based on Haar type multiresolution analysis (MRA). The advantage of using this technique is that we select a multiresolution analysis that is constructed according to the symmetries of the underlying space. Therefore, the new schemes of approximation take a lot of characteristics of the space into consideration. Note that the dyadic partition of the cube is a particular case of the MRA type Haar using translations and dilations of the underlying space.

The MRA is an important method to approximate functions in different context (signal processing, differential equations, etc.). In particular, we focus on Haar type MRA on ; the constructions of this kind of MRA are associated with the symmetries of the spaces; thus the approximations are related to the geometrical properties of the space. In this construction, the symmetries that we use are general dilations, rotations, reflections, translations, and so forth; for more details, see [4–6].

The main objective of this paper is giving a scheme of approximation of the MK problem based on the symmetries of the underlying spaces. We take a Haar type MRA constructed according to the geometry of our spaces. Thus, applying the Haar type MRA based on symmetries to the MK problem, we obtain a sequence of transportation problems that approximate the original MK problem for each level of MRA. Moreover, the optimal solutions of each level solution converge in the weak sense to the optimal solution of original problem.

This paper is organized as follows. In Section 2, we introduce the basic elements of the Haar type multiresolution analysis and we give some examples of this kind of MRA. In Section 3, we present the approximation of probability measures using Haar type MRA. In Section 5, we apply the Haar type multiresolution analysis to MK problem for each level of this MRA; thus for each level, this new problem is equivalent to transport problem. Moreover, we prove that the optimal solution of MK problems is equal to the limit of the optimal solutions of underlying transportation problems when the level of the MRA goes to infinity. Finally, we give an illustrative example of this method.

2. Haar Type Multiresolution Analysis

We introduce the basic concepts of Haar type multiresolution analysis, following Gröchenig and Madych in [4] and Guo et al. in [5]. Similar results have been obtained independently by Krishtal et al. to be published in [6].

Let Γ be a lattice such that

for any

. The classical multiresolution analysis (MRA) associated with a sequence of dilations

, where |det a | ≤ 1, is a sequence

of closed subspaces of

, which satisfies the following conditions:

(i)
V_k ⊂ V_k+1.
(ii)
.
(iii)
.
(iv)
.
(v)
There exists φ ∈ V₀ such that {T_γφ}, γ ∈ Γ, is an orthonormal basis for V₀.

Let B be a finite subgroup of

such that |det b | = 1 for all b ∈ B and Γ = B(Γ). The operator generator by the dilations D_b, b ∈ B, and the translations T_γ, γ ∈ Γ form a group. The relation

(1)

allows us to define the operation to B × Γ given by

(2)

and we obtain a new group denoted by BΓ. The BΓ-invariant spaces are the closed subspaces V of

such that D_bT_γf ∈ V whenever f ∈ V, b ∈ B, and γ ∈ Γ. This leads us to the following version of (v):

v^′ ) There exists φ ∈ V₀ such that {D_bT_γφ}, b ∈ B and γ ∈ Γ, is an orthonormal basis for V₀.

In consequence, we have the following concept.

Definition 1. Let be dilatation set, let B be a finite subgroup of with |det b | = 1, and let Γ be a complete lattice such that Γ = B(Γ). The multiresolution analysis associated with the dilation set A and the group B or AB-MRA is a collection of closed subspaces of , which satisfies conditions (i), (ii), (iii), (iv), and (v^′).

The classical MRA is considered as an AB-MRA when B is the trivial group. Note that the space V₀ is not generated by the Γ-translations of the single scaling function φ; however, the relation D_bT_γφ = T_bγD_bφ and the conditions B(Γ) = Γ imply that the functions D_bφ, with b ∈ B, are the generators of V₀. Also, we have the following set:

(3)

Note that Γ^j ⊂ Γ^j+1 and BΓ^j = Γ.

We consider the scaling function φ = Eχ_Δ, where χ_Δ is the characteristic function of

, and ‖φ‖₂ = 1. The region Δ satisfies

(4)

where

for α ≠ α^′ and Δ_α is the action of α = (b, γ) on Δ. In addition, the symbol

denotes the translation and scaling of the region Δ by α and a^j, respectively. Thus, the function

is denoted by

. And so we have the following relation:

(5)

Finally, we define P^j as the orthogonal projection from

to V_j which is given by

(6)

for all

We show some examples of the multiresolution analysis associated with the dilation set A and the finite group B:

(1)
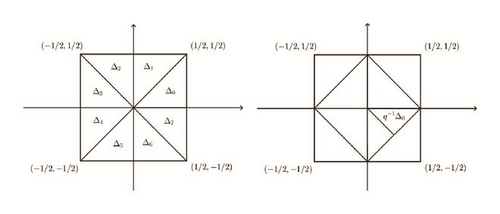
We take a matrix and the group B = {b_i}, 0 ≤ i ≤ 7, of symmetries of unit square; thus,
(7)
and b_i = −b_i−4 for 4 ≤ i ≤ 7. Let Δ₀ be the triangular region with vertices in (0,0), (1/2,0), and (1/2,1/2); we denote Δ_i = b_iΔ₀ for 1 ≤ i ≤ 7. If , then the system
(8)
is an orthogonal basis for its closed span V₀. The space V₀ is the subspace of , consisting of all square integrable functions that are constant on each -translate of the triangles Δ_i, 1 ≤ i ≤ 7. Thus, the spaces , , consist of all functions in , which are constant in each -translate of the triangles q⁻¹Δ_i, 1 ≤ i ≤ 7, in consequence V_j ⊂ V_j+1. Hence, {V_j} is an AB-MRA with φ as a scaling function.
Figure 1 is reproduced from Krishtal et al. (2007) [under the Creative Commons Attribution License/public domain].
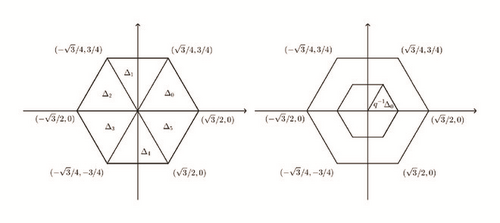
(2)
Let B be the group generated by the matrix . This group has order of 6 and is the counter-clockwise rotation by π/3 radians. Consider the hexagon with vertices in set
(9)
Let Δ₀ be the triangle with vertices in (0,0), , and . We define Δ_i = ρⁱΔ₀ for 0 ≤ i ≤ 5. We take and we define . The set of all functions that are constant on Γ-translates of triangles Δ_i, 0 ≤ i ≤ 5, is the space . Moreover, the elements of Γ translate the center of the hexagon to the point of Γ, and so we have a partition of . Let and the function , with . The MRA {V_j} is obtained by the system
(10)
where the spaces V_j are q^−j-dilatation of V₀, for .
Figure 2 can be found in [6].

Description unavailable — **Figure 1**
Open in figure viewer PowerPoint

3. Approximation of Measures Using Multiresolution Analysis

3.1. Absolutely Continuous Measures with respect to Lebesgue Measures

We consider the following conditions:

(A1)
X is a compact subset of .
(A2)
The measure μ is absolutely continuous with respect to λ, where λ is the Lebesgue measure.

Condition (A2) guarantees the existence of functions , where f is the Radon-Nikodym derivative with respect to Lebesgue measure λ.

In this analysis, we also assume the following extra condition:

(A3)
The functions f also belong in .

Notice that

(11)

Let {V_j} be an AB-MRA on ; the elements of {V_j} are given by scaling functions φ = E₁χ_Δ, the latice Γ, finite group B₁, and dilatation .

Remark 2. Note that the classical multiresolution analysis of Haar on is a particular case of AB-MRA on , where the complete lattice is , the group B is trivial, and the dilation associated is A = {2^−j(1,1)}. In this case, we have that scaling function is φ_Δ, where Δ = [0,1]×[0,1] is the fundamental domain associated with the action of Γ on .

We denote by P_j the projection from

into V_j, which is given by

(12)

for all

. Moreover, if the function f has support in X, then the above sum is finite, since X is compact.

From now on, we shall only functions with support in the compact set X and we have ; that is, each function can be considered in , where f(x) = 0 if x ∉ X.

We know that the AB-MRA is dense in

; thus we have that

(13)

Using the fact that X is compact, we obtain that

(14)

From the above equation, we define the approximation of the measure to the level j by

(15)

which are measures in X for each j. Now we want to prove that these measures are probability measures.

Definition 3. The expectation with respect to Lebesgue measure λ of function f is defined by

(16)

where f is a Lebesgue measurable function. Also, the conditional expectation of f given A, with A being a Lebesgue measurable set, is defined by

In particular, the expectation on the Lebesgue measure λ satisfies the following property.

Theorem 4. Consider that is fixed and . Then , where P_j is the projection of the level j associated with AB-MRA {V_j}.

Proof. We take ; now we calculate ; thus

(17)

We have that the functions

, where

is the translation and dilation of the fundamental region Δ and

; this value does not depend on α. From this, we have that

(18)

Using the above equations, we have that

(19)

Moreover, using the fact that

for α ≠ β, it is clear that

(20)

As immediate consequence of the previous theorem, we get the following result.

Corollary 5. We suppose that the measure μ on X satisfies (A1)-(A2); then the sequences of probability measures {μ^j} ⊂ M⁺(X) given by (15) converge to μ in and sense.

3.2. Non-Absolutely-Continuous Measures with respect to Lebesgue Measure

Now, we consider that μ is a probability measure on the compact set X, which is unnecessarily absolutely continuous measure with respect to Lebesgue measure λ. Note that each element of sequence (15) can be written by

(21)

for all Borel measurable sets U on X. Moreover, these approximations are well defined for every measure μ on X.

Definition 6. Let {μ_n; n ≥ 0} be a sequence of probability measures on a metric space (X, d). We say that μ_n converges weakly to μ and denote μ_n→_w μ if μ_n(f) → μ(f) as n → ∞ for all bounded continuous functions f on M, where μ(f) = ∫_M f dμ.

Theorem 7. Given a measure μ on the compact set X, the sequence of measures {μ^j} on X defined in (21) converge weakly to measure μ.

Proof. Let be a continuous and bounded real function. From the fact that X is compact, we obtain that f is absolutely continuous function on X; thus, given ϵ > 0, there exists δ > 0 such that

(22)

We take

such that for all

implies |x − y | < δ for all j ≥ j₀ and α ∈ BΓ. Moreover, we know that there exist α₁, …, α_r ∈ BΓ such that

(23)

In consequence, we obtain the following relations:

(24)

we take an element

to obtain the following relations:

(25)

Therefore,

(26)

4. Discretization of the Monge-Kantorovich Problem Using Multiresolution Analysis

Let M(X × Y) be the linear space of finite signed on X × Y and let M⁺(X × Y) be the set of all nonnegative measures in M(X × Y). Given μ ∈ M(X × Y), we denote by Π₁μ and Π₂μ the marginal of μ on X and Y, respectively; that is,

(27)

for all sets A and B, such that ν₁ and ν₂ are measurable, respectively.

The Monge-Kantorovich mass transfer problem is given as follows:

(28)

A measure μ ∈ M(X × Y) is said to be a feasible solution for MK problem if it satisfies (28) and 〈μ, c〉 is finite. The MK problem is called consistent if the set of feasible solutions is nonempty, in which case its optimal value is defined as

(29)

It is said that the MK problem is solvable if there is a feasible solution μ^∗ that attains the optimal value. In this case, μ^∗ is called an optimal solution for the MK problem and the value inf⁡(MK) is written as min⁡(MK) = 〈μ^∗, c〉.

Note that since ν₁ and ν₂ are probability measures, a feasible solution for MK is also a probability measure. Moreover, if c is a continuous function on X × Y and X and Y are compact subsets on , then the product measure μ≔ν₁ × ν₂ is a feasible solution. Therefore the MK problem is consistent, and so the MK problem is solvable in this case.

We assume the following conditions: X and Y are compact subsets of and is a bounded continuous function.

Let {V_j} and be AB-MRA on with scaling functions and , lattices Γ₁ and Γ₂, finite groups B₁ and B₂, and dilatations and , respectively. We can obtain a new AB-MRA on with scaling functions , lattice Γ = Γ₁ × Γ₂, finite group B = B₁ × B₂, and dilatation . The projections of these AB-MRA to the level j are denoted by , , and Q^j.

Now we proceed to discretization of the MK-problem using the results of Section 2; then we have that μ^j,

, and

are the projections to level j of the respective AB-MRA; thus, using these measures, we obtain the discretization of the MK-problem in the level j, which is given by

(30)

We shall give explicit expressions for the discretization of the measures and the cost function associated with MK-problem using the AB-MRA, which are given by

(31)

where

, and b_α,β are nonnegative real numbers. Now we calculate 〈μ^j, c〉; thus

(32)

and hence, using the above equation and the orthonormality of family

, we obtain

(33)

We consider that α_i is a fixed element in

and we have that

is the region associated with α_i for i = 1, …, r; then we obtain

(34)

On the other hand, we have that

(35)

From the above equations, we have that the condition

is equivalent to

(36)

Analogously, for all the elements β₁, …, β_s of

, we have that

(37)

Using Theorem 4, we obtain that

(38)

In summary, we have that the MK^j problem given by (30) is equivalent to the following problem:

(39)

The problem MKD^j, given the above system, has a feasible solution, so we know that c is bounded. Then we have that the problem MKD^j has an optimal solution; for more details, see Chapter 10 in [7].

Let μ_∗ be the optimal solution of MK problem given in (28). We use the optimal solution μ_∗ to induce a sequence of measures such that (see Section 3.2). Let be the optimal solution of MK^j problem given in (30).

For

, we defined the following σ-algebras:

(40)

where 〈A_i〉 _i∈I denotes the σ-algebra generated by the sets A_i with i ∈ I and the lattices

, and BΓ^j are defined as in (3).

Definition 8. Let be a sub-σ-algebra of , and let be a random variable. We say that the random variable X^′ is the conditional expectation of X with respect to and denote it by if and only if

(i)
.
(ii)
X^′ is -measurable.
(iii)
, for all .

Remark 9. Given , we have that

(41)

There are analogous results for

and

through the conditional expectations of

and

, respectively.

Proposition 10. Let μ be a feasible solution of the MK problem; then μ^j is a feasible solution of the MKD^j-problem.

Proof. We suppose that μ satisfies (28). Then we have the following relations:

(42)

where

and E a measurable set. Similarly, we obtain that

. Therefore the result is as follows.

Remark 11. If μ_∗ is an optimal solution of the MK problem, then is a feasible solution of the MKD^j-problem.

Proposition 12. Given and , one has

(43)

where μ and η^j are feasible solutions of the MK and MK^j problems, respectively.

Proof. Let be a generator element of σ-algebra . Then

(44)

In above equation, we use the fact that

for all

in consequence

for all

. Analogously, we have that

Definition 13. Let (X, τ) be a topological space, and let be σ-algebra on X that contains the topology τ. Let be a collection of measures defined on . The collection is called tight if, for any ϵ > 0, there is a compact subset K_ϵ of X such that, for all measures , |μ | (X∖K_ϵ) < ϵ, where |μ| is the total variation measure of μ.

Proposition 14. Consider the sequence of probability measures, where is the optimal solution of MK^j for each . Then there exists a subsequent and a probability measure η_∗ such that weakly. Moreover, the probability measure η_∗ is an optimal solution of MK.

Proof. We know that X₁ and X₂ are compact sets, provided that the measures are tight for each . Now, using Prokhorov’s Theorem (for details, see Chapter 1 in [8]), there exists a subsequence of and a probability measure η_∗ such that weakly.

Notice that is an optimal solution of ; thus, we obtain

(45)

Using the Theorem, we have that

and

weakly. From this fact, it is clear that η_∗ is a feasible solution of MK.

Now, we consider μ_∗ as the optimal solution of MK. from Proposition 10, we have that is feasible solution of MK^j. It follows that

(46)

taking the limit when j → ∞, we have

(47)

On the other hand, η_∗ is a feasible solution of MK; then

(48)

which completes the proof of the theorem.

5. An Illustrative Example of This Method

In this section, we present an example of the ideas presented in the previous section. Let C be the square with vertices in the points

(49)

and let H be a hexagon with vertices being in set

(50)

We consider the function

defined by c(x, y) = ‖x − y‖². We claim to solve the following problem:

(51)

where λ₁ and λ₂ are the normalized Lebesgue measures to C and H, respectively; that is, λ₁(C) = λ₂(H) = 1. We consider the following AB-MRA on

(1)
, where the fundamental region is Δ₁ = [0,1/2]×[0,1/2] and the scaling function φ₁ = 2χ_{[0,1/2]×[0,1/2]}, the lattice is , the finite group B₁ is the trivial group, and the dilation A₁ = {2^−j(1,1)}.
(2)
, where the scaling function , with Δ₂ being the triangle with vertices in (0,0), , and and ; the lattice is , where ; the finite group B₂ is the rotation group of a regular hexagon with vertices in the unit circle; the scaling is given by A₂ = {a^j}, where .

We denote by and the squares and the triangles associated with level j of the multiresolution analysis presented above. Since c is a continuous function in each pair of sets , we have that is approximated to , where and are the centroids of and , respectively.

In particular, we present a discretization of MK problem given by (51) for the level j = 2; the graphical description of the process of discretization is given in Figure 3 (which was generated using Mathematica 11.1.0).

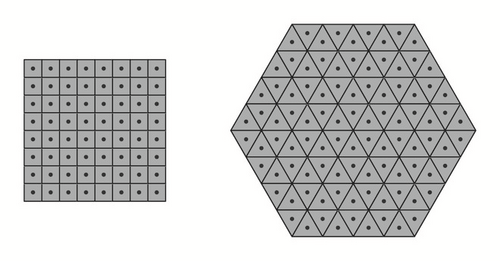
Using and in C and H, respectively, notice that C is the union of congruent squares with disjoined interiors. Similarly, the hexagon H is the union by congruent equilateral triangles , with disjoined interiors. Note that and .

In consequence, a discrete approximation for the problem defined in (51) is as follows:

(52)

The optimal solution of this linear programming problem is 4.02996. In Table 1 we present the solution for some levels.

Level	Solution
MK¹	4.037306413676646
MK²	4.029959684992724
MK³	4.026748275774876

6. Conclusions

The application of the Haar type multiresolution analysis (MRA) to the problem of Monge-Kantorovich allows us to obtain a discretization scheme for this problem at each level of the MRA; moreover, this MRA is based on the symmetries of the underlying space. This is an advantage because it provided us a natural method of discretization based on the geometry. Each level of the MRA induces a soluble finite linear programming problem. So, we obtain a sequence of optimal solutions of these transport problems and this sequence converges weakly to the optimal solution of the original problem.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this article.

Acknowledgments

This work was partially supported by the CONACYT project, México. The second author is grateful to Instituto Politécnico Nacional, México, for financial support for development of this work.

References

1 Hernández-Lerma O. and Lasserre J. B., Approximation schemes for infinite linear programs, SIAM Journal on Optimization. (1998) 8, no. 4, 973–988, https://doi.org/10.1137/S1052623497315768, MR1641282.
10.1137/S1052623497315768
Web of Science® Google Scholar
2 González-Hernández J., Gabriel J. R., and Hernández-Lerma O., On solutions to the mass transfer problem, SIAM Journal on Optimization. (2006) 17, no. 2, 485–499, https://doi.org/10.1137/050623991, MR2247747.
10.1137/050623991
Web of Science® Google Scholar
3 Gabriel J. R., González-Hernández J., and López-Martínez R. R., Numerical approximations to the mass transfer problem on compact spaces, IMA Journal of Numerical Analysis. (2010) 30, no. 4, 1121–1136, https://doi.org/10.1093/imanum/drn076, 2-s2.0-77958164489.
10.1093/imanum/drn076
Web of Science® Google Scholar
4 Gröchenig K. and Madych W. R., Multiresolution analysis, Haar bases, and self-similar tilings of Rn, Institute of Electrical and Electronics Engineers Transactions on Information Theory. (1992) 38, no. 2, 556–568, https://doi.org/10.1109/18.119723, MR1162214.
10.1109/18.119723
Google Scholar
5 Guo K., Labate D., Lim W.-Q., Weiss G., and Wilson E., Wavelets with composite dilations and their MRA properties, Applied and Computational Harmonic Analysis. (2006) 20, no. 2, 202–236, https://doi.org/10.1016/j.acha.2005.07.002, MR2207836.
10.1016/j.acha.2005.07.002
Web of Science® Google Scholar
6 Krishtal I. A., Robinson B. D., Weiss G. L., and Wilson E. N., Some simple Haar-type wavelets in higher dimensions, The Journal of Geometric Analysis. (2007) 17, no. 1, 87–96, 2-s2.0-34147156660, https://doi.org/10.1007/BF02922084, Zbl1124.42026.
10.1007/BF02922084
Web of Science® Google Scholar
7 Bazaraa Mokhtar S., John J., and Hanif D., Linear Programming and Network Flows, 2009, Wiley.
10.1002/9780471703778
Google Scholar
8 Billingsley P., Convergence of Probability Measures, 1968, Wiley, New York, NY, USA, MR0233396, Zbl0172.21201.
Google Scholar

All articles

Multiresolution Analysis Applied to the Monge-Kantorovich Problem

Abstract

1. Introduction

2. Haar Type Multiresolution Analysis

3. Approximation of Measures Using Multiresolution Analysis

3.1. Absolutely Continuous Measures with respect to Lebesgue Measures

3.2. Non-Absolutely-Continuous Measures with respect to Lebesgue Measure

4. Discretization of the Monge-Kantorovich Problem Using Multiresolution Analysis

5. An Illustrative Example of This Method

6. Conclusions

Conflicts of Interest

Acknowledgments

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Multiresolution Analysis Applied to the Monge-Kantorovich Problem

Abstract

1. Introduction

2. Haar Type Multiresolution Analysis

3. Approximation of Measures Using Multiresolution Analysis

3.1. Absolutely Continuous Measures with respect to Lebesgue Measures

3.2. Non-Absolutely-Continuous Measures with respect to Lebesgue Measure

4. Discretization of the Monge-Kantorovich Problem Using Multiresolution Analysis

5. An Illustrative Example of This Method

6. Conclusions

Conflicts of Interest

Acknowledgments

References

Figures

References

Related

Information