A Novel Autonomous 5-D Hyperjerk RC Circuit with Hyperbolic Sine Function

1. Introduction

The study of three-dimensional dynamical systems seems to be mature [1–15]. The interest is now focused on high dimensional systems [16–21]. The reason is that they have been discovered to model natural phenomena more explicitly than the three-dimensional dynamical systems. Recently, hyperjerk systems have received great attention. In 2005, Konstantinos and Sprott proposed a class of chaotic/hyperchaotic hyperjerk systems [19]. They investigated the dynamical properties of the proposed systems focusing on potential chaotic and hyperchaotic dynamics. They also claimed to have proposed surprisingly simple and most elegant functional forms of hyperjerk systems. A year later, Stefan showed that the concept of hyperjerk systems might serve as an appropriate starting point to study the dynamics of driven or coupled oscillators in a unified way [22]. The five-dimensional (5-D) hyperchaotic Sprott B system has ten terms including two quadratic nonlinear terms and only one control parameter. Hong Mey and collaborators have recently proposed a novel cryptosystem based on 5-D hyperchaotic system [23]. The system is combined with the logistic map for the generation of pseudo random sequences of better properties. In order to analyze the behavior of chaotic systems, some researchers focused on the synchronization and control of the 5-D systems [23–26]. These systems are algebraically simpler than Lorenz and Lorenz-like 5-D systems with twelve terms, three quadratic nonlinear terms including five or six control parameters. Let us note that the practical realization of quadratic nonlinearity found in these works is expensive due to the presence of analogue multipliers. Recently multistability has attracted tremendous research efforts [1, 5, 12]. However to the best of the author’s knowledge, multistability in 5-D hyperjerk systems is very little documented. Also it is very interesting to question whether there exists a simple chaotic 5-D hyperjerk system capable of multiple coexisting attractors.

This paper investigates the dynamics of a novel 5-D hyperjerk circuit with a very simple nonlinear part (a pair of semiconductor diodes). The new circuit can be regarded as a 5-D version of the jerk circuit previously reported by Kengne and collaborators [27]. It is important to stress that the simplicity of the 5-D autonomous circuit relies on the practical standpoint where the nonlinear part is constructed using semiconductor diodes. Despite the relative simplicity of their electronic circuits, the proposed circuit is characterized by rich and striking nonlinear behaviors such as chaos, antimonotonicity, multiple coexisting attractors.

The paper is organized as follows: Section 2 deals with the modeling process. The electronic structure of the oscillator is described and a suitable mathematical model is derived to investigate the dynamics of the system. Section 3 is concerned with the numerical analysis. Various bifurcation diagrams combined with their corresponding graphs of the largest Lyapunov exponent are plotted to reveal different transitions to chaos. The occurrence of multiple attractors is also discussed using bifurcation diagrams as arguments. In addition the bubbling phenomenon is presented. Pspice circuit simulations results are carried out in Section 4. Some concluding remarks are presented in Section 5.

2. Presentation of the Novel 5-D Circuit

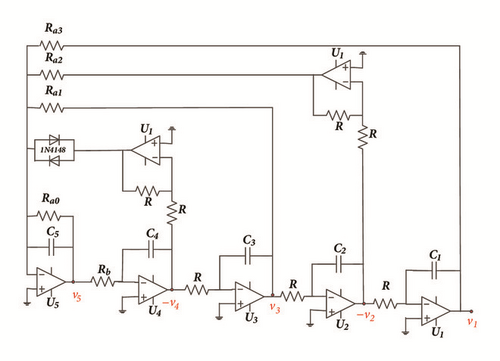
System (3) is dissipative since its divergence (∇V = −a₀) is negative. Consequently, all system orbits will be confined to a specific bounded subset of zero volume in state space and the asymptotic dynamics converges to an attractor. This is true for this particular case. However, the system is dissipative in the sense of Levinson if there exists nonlocal Lyapunov function which defines the absorbing set [23]. In addition, System (3) is invariant under the transformation: (x₁, x₂, x₃, x₄, x₅)⇔(−x₁, −x₂, −x₃, −x₄, −x₅). Consequently, if (x₁, x₂, x₃, x₄, x₅) is a solution of system (3) for a given set of parameters, then (−x₁, −x₂, −x₃, −x₄, −x₅) is also a solution for the same parameter set. This property is responsible for the variety of coexisting attractors in the system. Finally, it is found that the novel oscillator under investigations has only one equilibrium point that is the origin E₀(0,0, 0,0).

3. System’s Dynamics

3.2. Route to Chaos and Antimonotonicity

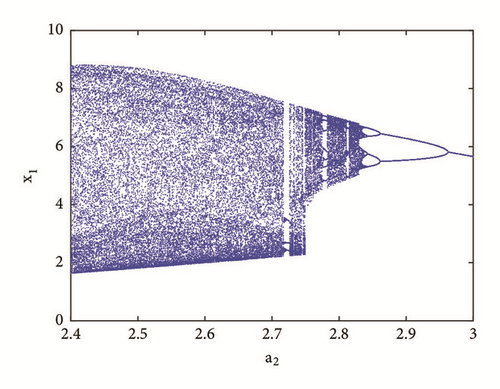
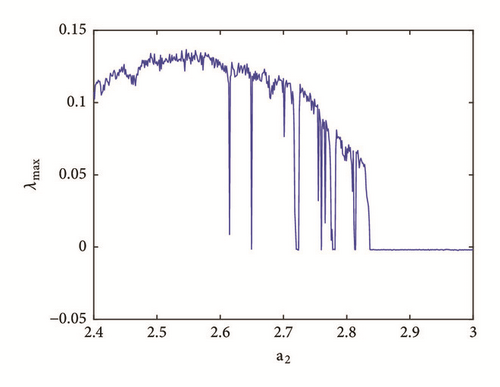
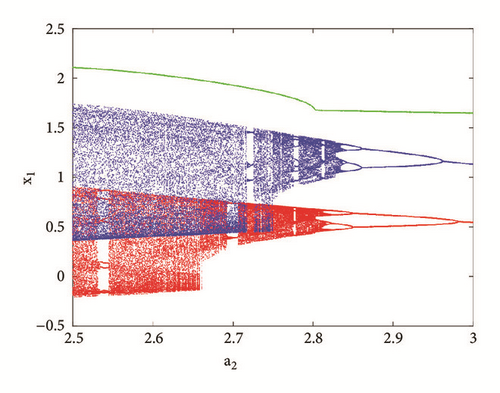
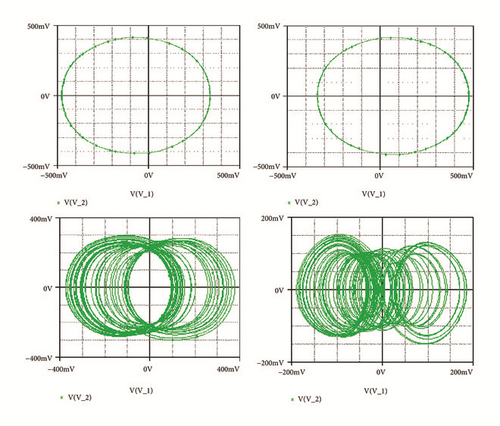
To reveal the type of transition leading to chaos, a single control parameter (b) was considered to vary in the range 2.4 < a₂ < 3 while the rest of system’s parameters are fixed as follows: a₀ = 1.75; a₃ = 1; a₁ = b = 3; γ = 0.0011. The bifurcation diagram of Figure 2 is obtained by forward continuation. From this diagram it is obvious that the system experiences the classical reverse period doubling bifurcation. It moves from period-1 limit cycle to double band chaotic attractors going through single band chaotic attractors and tiny windows of periodic attractors. Figure 3 (left) illustrates this bifurcation sequence with the numerical phase portraits.

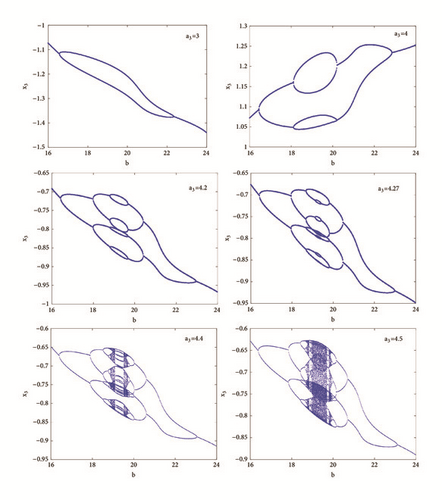
As the system experiences the classical period doubling route to chaos, it is obvious that antimonotonicity can be observed. Represented on Figure 4, this behavior has been searched by varying parameter b in the range 16 to 24 for some discrete values of parameter a₃. For instance, if a₃ = 3 period-2 bubble is observed and each branch develops two branches leading to a stable period-4 bubble for a₃ = 4. Similarly a period-8 bubble is obtained for a₃ = 4.2. As the discrete parameterb increases, more bubbles are created until an infinitely tree (chaos) finally occurs when a₃ = 4.5.

3.3. Multiple Coexisting Attractors

Multistability has been previously revealed in many dynamical systems [29–34], including jerk systems with self-excited attractors [30, 33, 34] and hidden attractors [3, 6, 35]. But the models presented up to date achieved at most six coexisting attractors in the phase space. This behavior has not yet been discovered in any 5-D hyperjerk systems. The system under study can challenge this limit by displaying up to seven coexisting attractors depending solely on the system’s initial state.

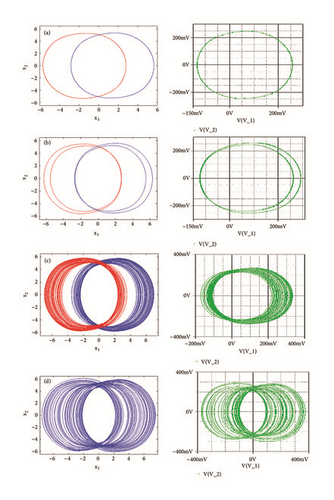
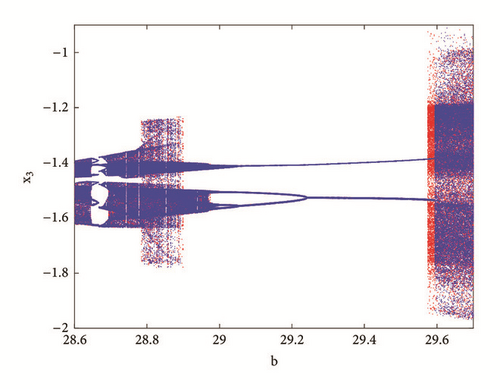
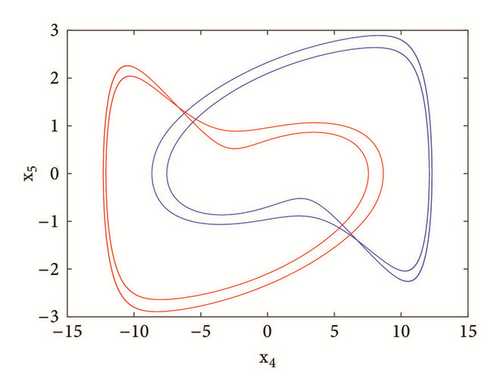
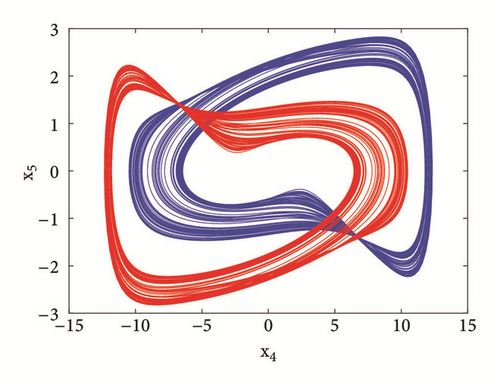
With reference to the bifurcation diagram of Figure 5 the classical forward or backward continuation of parameter b is obtained with the following initial conditions x₁(0) = 3; x₂(0) = x₃(0) = x₄(0) = x₅(0) = 0 and x₁(0) = 1; x₂(0) = x₃(0) = x₄(0) = x₅(0) = 0. A hysteretic window can be identified leading to the coexistence of four disconnected chaotic and periodic attractors (Figure 6) in the phase space for b = 29.57, a₀ = a₂ = a₃ = 5, a₁ = 7, γ = 5.4433x10⁻⁴.

Table 1. Comparative analysis of some dynamical systems by using the largest Lyapunov exponent (λmax).

References	Dynamical system	Parameters	Maximum Lyapunov exponent  λmax
[16]	$$	a = 10	λmax = 0.4195
	$$	$$
	$$	c = 28,   p = 1.3
	$$	q = 2.5
	$$
[17]	$$	a = 4	λmax = 0.1589
	$$	γ = 0.06,   μ = 0.75
	$$
[21]	$$	a = 0.25,   b = 3	λmax = 0.112
	$$	c = 0.5,   d = 0.05
	$$
	$$
[23]	$$	a = 10,   r = 28	λmax = 0.39854
	$$	$$
	$$
	$$
This work	$$	b≔32	λmax = 0.82
	$$	a0 = 5,   a1 = 7
	$$	a2 = 5,   a3 = 4.50
	$$	a4 = 5.4433 × 10−4
	$$

Table 2. Initial conditions for the abundant coexisting attractors.

Figures	Type of coexistence	Dimensionless parameter	Corresponding electronics components	Numerical initial conditions  (x10, x20, x30, x40, x50)	Pspice initial conditions  (υ10, υ20, υ30, υ40, υ50)
6	Four disconnected chaotic attractors	b = 29.18	Rb = 342.7Ω	(a)  (1,0, 0,0, 0)  (b)  (3,0, 0,0, 0)	–
8&14	Four disconnected chaotic and periodic attractors	a2 = 2.458	Ra2 = 17.91kΩ	(a)  (±6,0, 0,0, 0)  (b)  (2,0, 0,0, 0)  (c)  (3,0, 0,0, 0)	(a-b)  (±0.3,0, 0,0, 0)  (c-d)  (±1,0, 0,0, 0)  (e)  (0,0, 0.2,0, 0)
10	Five disconnected chaotic and periodic attractors	a2 = 2.71	Ra2 = 14.65kΩ	(a)  (±5,0, 0,0, 0)  (b)  (±0.6,0, 0,0, 0)  (c)  (5.6,0, 0,0, 0)	(a-b)  (±0.2,0.1,0.1,0.2)  (c-d)  (±0.5,0.1,0.1,0.2)  (c-d)  (±0.5,0.1,0.1,0.2)
9&15	Five disconnected periodic attractors	a2 = 3	Ra2 = 15.6kΩ	(a)  (±5,0, 0,0, 0)  (b)  (±0.6,0, 0,0, 0)  (c)  (5.6,0, 0,0, 0)	(a-b)  (±0.1,0, 0,0, 0)  (c-d)  (±0.2,0, 0,0, 0)  (e-f)  (±0.3,0, 0,0, 0)
11&16	Six disconnected chaotic and periodic attractors	a2 = 2.8	Ra2 = 16.5kΩ	(a)  (±0.45,0, 0,0, 0)  (b)  (±0.6,0, 0,0, 0)  (c)  (±0.35,0, 0,0, 0)	(a-b)  (±0.1,0, 0,0, 0)  (c-d)  (±0.2,0, 0,0, 0)  (e-f)  (±0.3,0, 0,0, 0)
13	Seven disconnected chaotic and periodic attractors	a2 = 2.834	Ra2 = 35.28kΩ	(a)  (1,0, 0,0)  (b)  (±3,0, 0,0)  (c)  (±2,0, 0,0)  (d)  (4,0, 0,0)	–

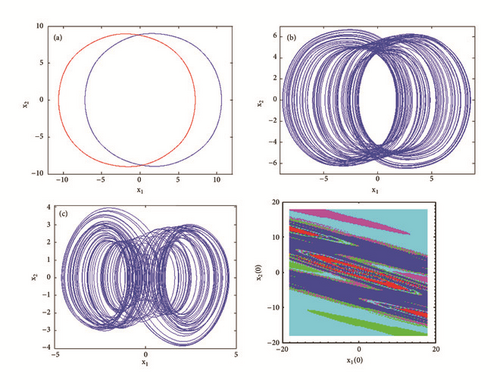
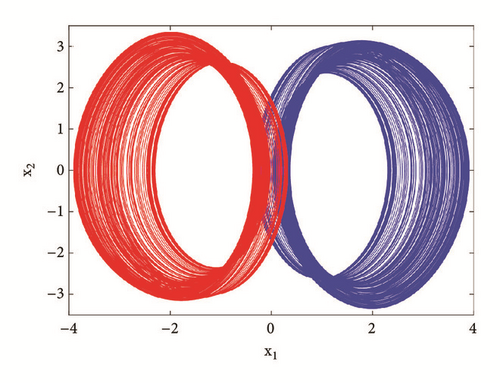
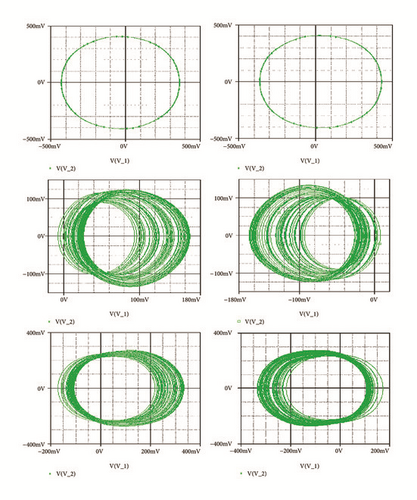
To observe more than four different attractors in the system, the second method described above (see Section 3.2) is used to plot the bifurcation diagrams of Figures 7 and 12 by varying parameter a₂. If we fix systems parameters as a₂ = 2.458; a₀ = 1.75; a₁ = b = 3; a₃ = 1; γ = 0.0054, the system experiences four different periodic and chaotic attractors (see Figure 8) where the cross section of the basins of attraction of the attractors is also presented. This dynamics is justified using the bifurcation diagrams of Figure 7.

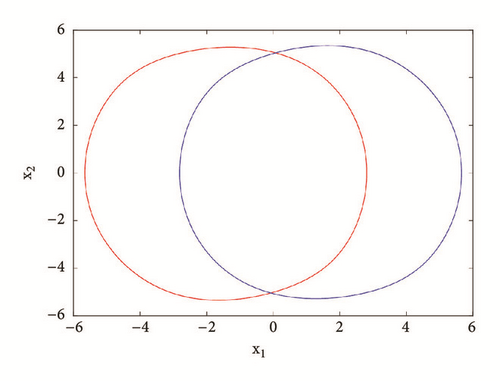
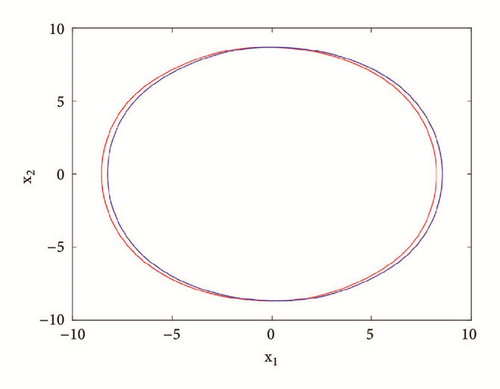
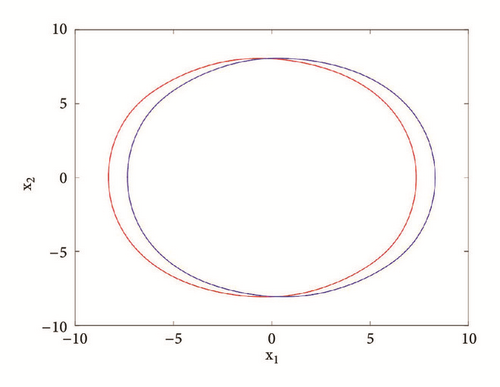
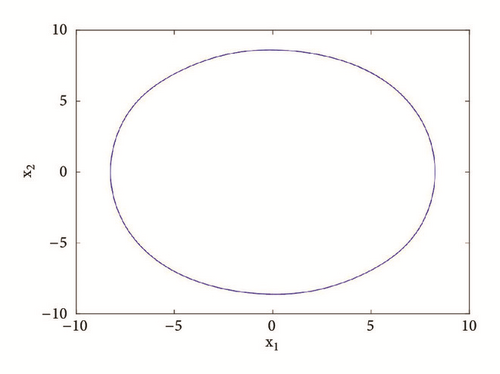
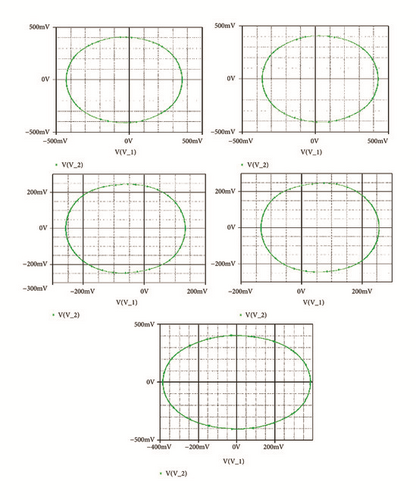
If systems parameters are a₂ = 3; a₀ = 1.75; a₁ = b = 3; a₃ = 1; γ = 0.0054, the system displays five different period-1 limit cycles (see Figure 9). This dynamics is justified using the bifurcation diagrams of Figure 7.

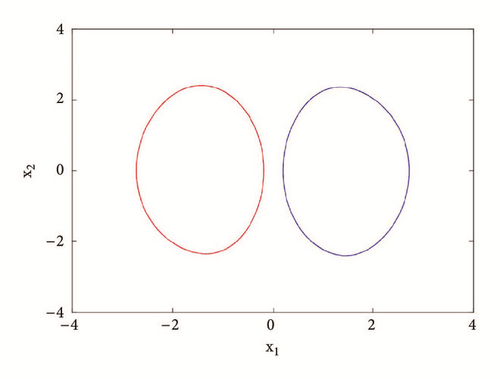
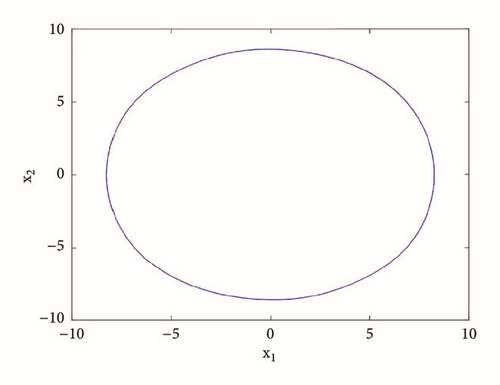
For a₂ = 2.71; a₀ = 1.75; a₁ = b = 3; a₃ = 1; γ = 0.0054, the system experiences five different periodic and chaotic attractors (see Figure 10). This dynamics is justified using the bifurcation diagrams of Figure 7.

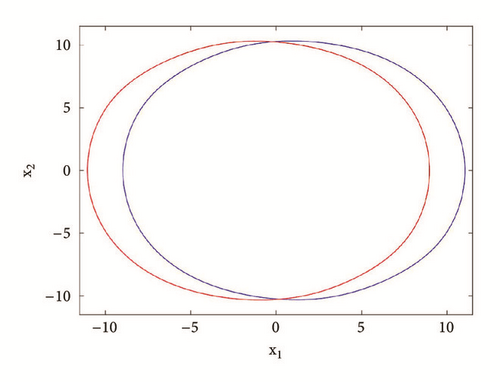
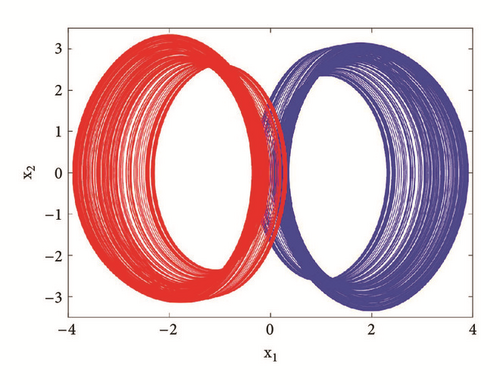
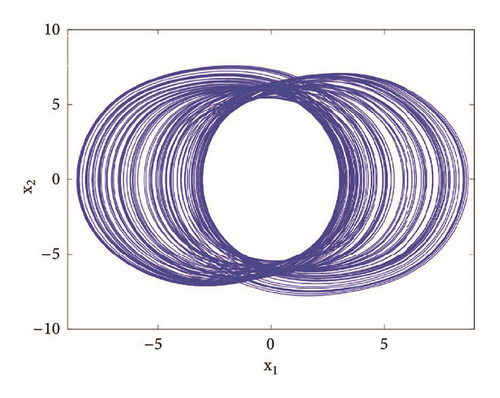
For a₂ = 2.8; a₀ = 1.75; a₁ = b = 3; a₃ = 1; γ = 0.0054, the system displays six different periodic and chaotic attractors (see Figure 11). This dynamics is justified using the bifurcation diagrams of Figure 7. The corresponding attraction basin is shown in Figure 7. Let us note that an attractor is hidden if their basin of attraction does not intersect with small neighborhoods of the equilibrium points of system. Given that the single equilibrium point of system (3) E₀(0,0, 0,0) intersects with the basin of attraction of the coexisting attractor Figure 7, we can conclude that the said attractor is self-excited (instead of hidden attractors). Some literature can provide systems with hidden attractors [3, 6, 35].

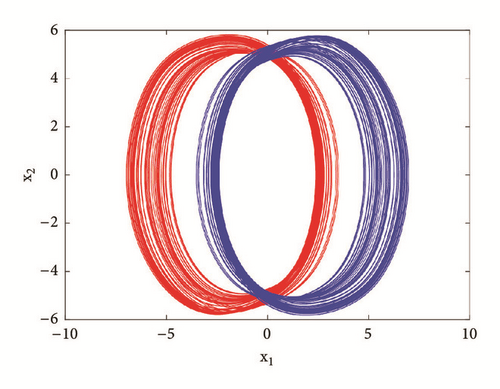
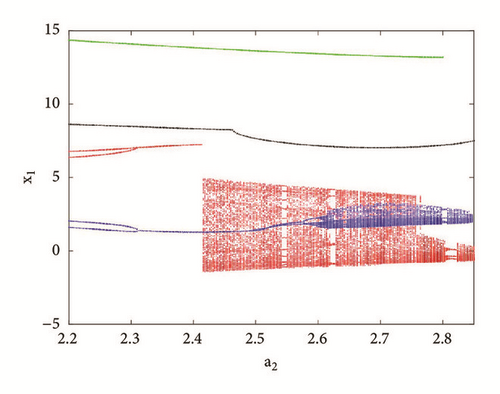
More interestingly, another window of multiple coexisting attractors can be revealed when a₀ = 1.75; a₁ = b = 3; a₃ = 1; γ = 0.0109 and the control parameter a₂ is varied in a tiny range. The bifurcation diagrams of Figure 12 revealed a window in which up to seven disconnected attractors (see Figure 13) coexist in the phase space depending solely on the system’s initial state. Table 2 provides the initial conditions for these coexisting attractors.

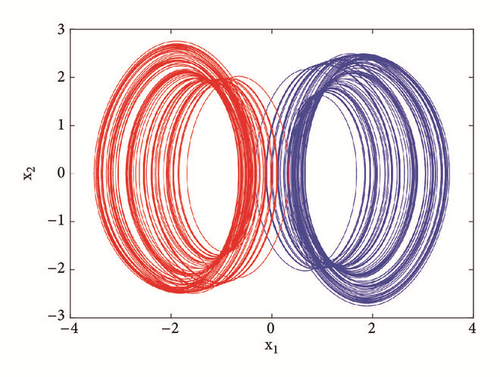
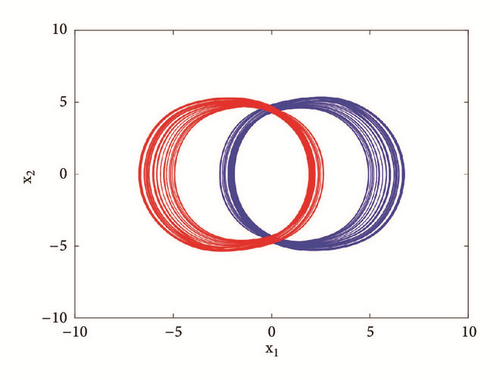
This work represents an enriching contribution to the understanding of the nonlinear dynamics of this type of oscillators [36]. However, this striking phenomenon of disconnected coexisting attractors is also reported in other nonlinear dynamic systems such as lazer system [37], chemical reaction [38], and the radio physical system [35]. A special case where infinitely many attractors coexist, also referred to as extreme multistability, is discussed in [26, 39]. The multiplicity of attractors represents an additional type of randomness [40] that is exploited in real applications such as chaos based secret communication, image encryption, and random signal generation as well. However, this type of behavior is not desirable in general, thus the need for control. Detailed analysis on this line is out of the scope of this paper. Also, we suggest the excellent work on control of multistability by [41] to interested readers.

4. Pspice Circuit Simulations

Our motivation in this section is to verify the theoretical/numerical results obtained previously by performing some Pspice based simulations of the circuit. Furthermore, it is important to evaluate the effects of simplifying assumptions (e.g., ideal diode model and ideal op. amplifiers) considered during the mathematical modeling process, on the behavior of a hardware prototype of the 5-D hyperjerk circuit in Pspice. Briefly recall that an interesting aspect of using Pspice is the possibility of setting initial capacitors’ voltages and analyzing the corresponding influence on the dynamics of the complete electronic circuit. Thus, the presence of multiple coexisting attractors can be tracked in a straightforward manner.

First to report the reverse period doubling routes to chaos observed during the numerical analysis, the circuit of Figure 1 has been simulated with the following electronic components: R = 10kΩ, C = 10ηF, R_a0 = 5.71kΩ, R_a1 = R_b = 3.33kΩ, R_a3 = 10kΩ. By varying R_a2, the complete routes to chaos are obtained and depicted in Figure 3-right. For R_a2 = 15.5kΩ a period-1 limit cycle is obtained, for R_a2 = 16.2kΩ a period-2 limit cycle is obtained, and chaotic attractors are obtained for R_a2 = 17kΩ and R_a2 = 18kΩ.

Secondly, coexistence of multiple attractors can also be confirmed by Pspice based simulations with the following electronic circuit components: R = 50kΩ, C = 2ηF, $$; $$. If R_a2 is fixed to R_a2 = 17.91kΩ, four disconnected chaotic and periodic attractors (see Figure 14) coexist depending solely on the system’s initial states as indicated in Table 2. For R_a2 = 15.6kΩ, five different period-1 limit cycles can be observed (see Figure 15). The corresponding initial states are indicated in Table 2. If R_a2 is fixed to R_a2 = 16.5kΩ, six disconnected chaotic and periodic attractors (see Figure 16) coexist depending solely on the system’s initial states as indicated in Table 2. A very good similarity between numerical phase portraits and Pspice simulation results can be observed. However, slight discrepancies that may be attributed to the simplifying assumptions adopted during the modeling process can be noted between the bifurcations points in Pspice compared to the results from the theoretical analysis. It is important to stress that while Pspice software is based on actual circuit components, it still suffers from the discretization and its use can lead to wrong conclusions especially for hidden attractors (the same is true for MATLAB) [42].

5. Conclusion

A novel 5-D hyperjerk circuit with a very simple nonlinear part has been introduced in this work. The circuit is obtained by introducing additional feedback loops in the realization circuit of a jerk system previously reported by J. Kengne and collaborators. The modification yields the simplest 5-D hyperjerk system reported up to date. More interestingly, for some given sets of parameters, the system experiences a plethora of multiple coexisting attractors. For instance, up to seven disconnected attractors coexist in the system depending solely on the initial conditions. To the best of author’s knowledge, such dynamics has not yet been reported in any hyperjerk system and thus deserves dissemination. Pspice based simulations were carried out to support the theoretical analysis. A detailed exploration of the parameter space (both experimentally and numerically) in view of revealing hyperchaotic behavior and hidden attractors in system (3) deserves further studies.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.