This paper proposes a novel robust output feedback control methodology for the course keeping control of a fully submerged hydrofoil vessel. Based on a sampled-data iterative learning strategy, an iterative learning observer is established for the estimation of system states and the generalized disturbances. With the state observer, a feedback linearized iterative sliding mode controller is designed for the stabilization of the lateral dynamics of the fully submerged hydrofoil vessel. The stability of the overall closed-loop system is analyzed based on Lyapunov stability theory. Comparative simulation results verify the effectiveness of the proposed control scheme and show the dominance of the disturbance rejection performance.

1. Introduction

As an advanced marine vehicle, the fully submerged hydrofoil vessel (FSHV) can cruise at a high speed against rough sea waves. The lift force of the hydrofoils generated by the high-speed fluid elevates the ship hull up from the water, which highly reduces the wave resistance and friction on the ship. However, the lift force also destabilizes the open-loop system of the FSHV. Therefore, it is necessary to equip an autopilot for this type of marine vehicles [1–3]. Currently, the commercial control systems equipped on board are based on optimal control theory [4], which has a weak disturbance rejection property. For the sake of the high cruising speed, the nonlinear hydrodynamic damping of the FSHV cannot be neglected [5, 6]. Therefore, the widely used linear model of marine surface vessels is no longer applicable given the strong coupling between yaw and roll dynamics. Moreover, the model uncertainties and disturbances caused by wind, waves, and currents prevent precise steering of this species of marine vehicle.

The path of marine surface vehicles is usually a straight line or straight lines formed by waypoints at the open sea. Hence, there is little coupling between the longitudinal dynamics and the lateral dynamics. Some literatures present the riding control design of the FSHV [4, 7]. This paper mainly focuses on the steering control of the FSHV.

For the nonlinear steering control of marine vessels, a series of control methodologies have been proposed, such as advanced sliding mode control [8–10], robust control [11, 12], and adaptive control [13, 14]. But these passive disturbance attenuation control methods may suffer from actuator chattering, system conservation, derivative explosion, and rigorous proof for stability. Intelligent approximation tools such as neural network, fuzzy logic, and SVM are introduced as feedforward components for state estimate and disturbance compensation, but the convergence rate of weight function and the problem of extremum solving still remain to be settled [6, 12].

Disturbance rejection control is also widely used in applications of rigid body dynamics and servo systems [15–17]. Disturbance observer based control (DOBC) approaches provide an active way to handle disturbances and improve the robustness of the closed-loop systems. The effectiveness of DOBC has been shown in many fields such as manipulator tracking control [18], missile guidance and control [19–21], and motor control [22, 23]. However, traditional DOB methodology cannot be used in nonlinear dynamics due to the limitation of linear system theory, and the low pass filter must be designed strictly such that the convergence of the disturbance estimate can be guaranteed [16].

Most of the methodologies for motion control of marine vehicles in the existing literatures employ full-state feedback. In many practical applications, only angle signals can be measured and utilized [24–32] since the sensor information of angle velocity usually contains irregular noises caused by the environment and properties of electric components, which are difficult to filter [5, 33]. Therefore, it is necessary to design a state observer to make state estimation for the system. State observer based control schemes have been developed for many species of nonlinear systems such as nonlinear time-delay systems [34, 35], Lipschitz nonlinear systems [24, 26, 36], and other structured systems [15, 27, 28]. According to the design theory, state observers can be classified, for example, as Luenberger observer [29, 36], high-gain observer [30], and sliding mode observer [31, 32]. For nonlinear systems with model uncertainties and external disturbances, there are the following disadvantages of these above-mentioned state observers.

(1)
In most control engineering applications, the system structures do not match these observers very well, so the observers require complicated coordinated transformations.
(2)
Many state observer methodologies are designed for SISO systems, but the practicality and stability of these methodologies for MIMO systems still need to be further discussed.
(3)
Most of these observers estimate only the system states, while the disturbance estimate could not be overall considered.

The course keeping control of the FSHV suffers severely from model uncertainties and wave disturbances. Therefore, it is of great necessity to design an observer which is able to estimate system states as well as the generalized disturbances integratedly. Furthermore, in order to guarantee the disturbance rejection performance of the control scheme, the feedback controller of the inner loop should also achieve disturbance attenuation properties, such that the residual error of the disturbance estimate can be compensated through a composite strategy.

In this paper, a novel output feedback control methodology is proposed for the course keeping control of the FSHV based on a sampled-data iterative learning approach. An iterative learning observer is established for the state estimation as well as generalized disturbances. Then a sliding model controller with an iterative learning sliding manifold is presented for the stabilization of the lateral dynamics of the FSHV. The design of the iterative sliding surface introduces a memory effect for the controller, which includes both the current and past information of the system states and outperforms the standard sliding mode control in the improvement of the transient performance.

The rest of the paper is organized as follows. In Section 2, the mathematical model of the lateral dynamics of the FSHV is established. In Section 3, an observer based sliding mode control is proposed based on iterative learning approach. Then we analyze the Lyapunov stability of the overall closed-loop system in Section 4. Simulation is carried out in Section 5 to validate the effectiveness of the proposed methodology, followed by Conclusions in Section 6.

2. Problem Formulation

A typical configuration of a fully submerged hydrofoil vessel is shown in Figure 1 [4]. The T-shaped bow foil is equipped with two controlled flaps, acting together. The aft foil has a pair of central flaps and two pairs of ailerons. Struts of the aft foil are equipped with rudders, which are used for roll and yaw dynamics together with the ailerons. The bow foil and the central part of the aft foil are for longitudinal motion control.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Fully submerged hydrofoil vessel.

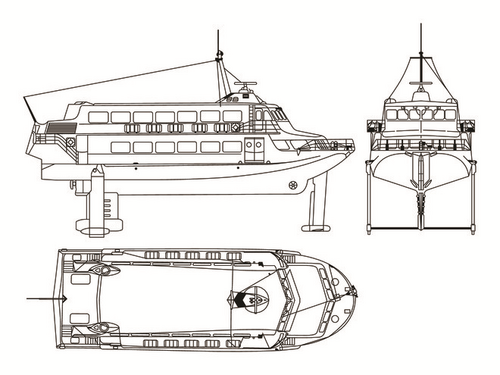
Course keeping control, or so-called ship heading control, is the primary task of the autopilots of ships. The control objective of course keeping control is to stabilize the yaw angle to a desired heading angle. As to the course keeping control for conventional marine surface vessels, the roll dynamics is rarely considered due to the weakness of the control actuators for roll dynamics. The roll restoring moments provide static stability, which the FSHV does not have. Therefore, it is necessary to take the roll dynamics into consideration for the course keeping control design for the FSHV.

The surge speed u is usually controlled by an individual propulsion system and is kept at a fixed speed u₀ when a ship is maneuvered in the course keeping mode. Accordingly, a 2-DOF steering model of the FSHV is shown as

(1)

where η = [ϕ, ψ]^T, in which ϕ and ψ denote the roll angle and heading angle of the FSHV with coordinates in the earth-fixed frame, respectively; υ = [p, r]^T, in which p and r represent the angular velocities with coordinates in the body-fixed frame, respectively;

is the Jacobian transformation matrix related to the above frames;

is the inertia including added mass; and

denotes the Coriolis and centripetal matrix. Selecting the origin point of the body-fixed frame at the center of gravity yields x_g = 0. D(u₀, ν) is the coupling interaction caused by the nonlinear hydrodynamic damping, which is defined as D = D_L + D_N.

stands for the linear part and

represents the nonlinear damping, respectively. K_p, K_rϕϕ, K_r, K_rϕϕ, and N_rϕϕ, N_p, N_r, N_rrϕ are the hydrodynamic coefficients. In the low-speed mode, the high-order terms and coupling interactions among the forces from each DOF are not considered. Therefore, D(u₀, ν) is often regarded as a linear term and even cancelled in many literatures. However, given the high-speed character of the FSHV, the nonlinear damping hydrodynamics can no longer be neglected. G(η) represents the gravity term which is described as

, where W = mg is the weight and

is the transverse metacenter height [37].

is the control moment coefficient matrix subjected to the control surface, and

is the control input, where δ_R and δ_A represent the rudder angle and aileron angle of the hydrofoil system, respectively. As for the modeling of the FSHV, it is reasonable to select the origin point of the body-fixed frame at the center of gravity, thus yielding x_g = y_g = z_g = 0.

Considering the course keeping problem of the FSHV, the first equation in (1) can be simplified as

. By defining x₁≜η, x₂≜υ, the steering model of the FSHV can be regarded as a second-order system as

(2)

where

(3)

If the model uncertainties are considered in the modeling and control of the FSHV, the following notations are introduced:

(4)

where subscript 0 denotes the nominal part of the corresponding matrix and the subscript Δ represents the perturbed part of the system dynamics. The yaw/roll dynamics of the FSHV with model uncertainties can be rewritten as follows:

(5)

where

is the generalized disturbances of the system.

Remark 1. When ships sail at a fixed speed, M(·), C(·), D_L(·), and G(·) are linear matrices with constant element parameters, so F₀(x₁, x₂) is also a linear function, while ζ₀(x₁, x₂) represents the nonlinear damping of the coupling hydrodynamics of the FSHV.

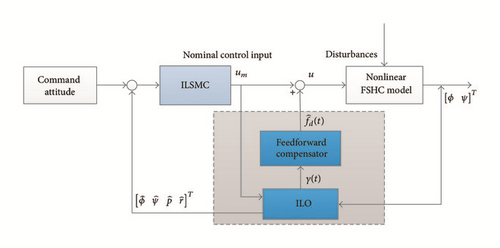
Hence, the control objective is to design an observer based output feedback controller for the course keeping of the FSHV using an iterative learning approach. The control structure of the system is summarized in Figure 2. For the subsequent analysis, the following assumptions are carried out for convenience.

Assumption 2 (see [25]–[28], [37].)The nonlinear function ξ(·) is continuously differentiable and satisfies Lipschitz condition with Lipschitz constant σ; that is,

(6)

Remark 3. For marine vehicle systems, the high-order coupling hydrodynamics is sufficiently smooth. Therefore, it is reasonable that the nonlinear function ξ(·) satisfies Lipschitz condition.

Assumption 4. The disturbance f_d(t) is bounded; namely, .

3. Output Feedback Control Design of the FSHV

3.1. Iterative Learning Observer Design

In this section, an iterative learning observer (ILO) is established for estimation of system states as well as the disturbances. To facilitate the subsequent design, the system dynamics in (5) are rewritten into a generalized state space model as

(7)

where

, and

, y = x₁.

Based on (7), an ILO is designed as

(8)

where

is the estimation value of x,

is the estimation of system output at time t, τ is the sampling time interval, γ is called ILO input, γ(t) is the current ILO input and γ(t − τ) is the ILO input at the last sampling period. L and μ_i (i = 1,2) are two gain matrices with appropriate dimensions to be determined.

Remark 5. It can be seen from (8) that if the gain matrix μ₁ is selected as a zero matrix, the ILO will degenerate into a conventional Luenberger observer. Therefore, zero matrix should be avoided for the gain tuning in order to maintain the capability of the estimation for the generalized disturbance.

Remark 6. It is necessary to clarify that the ILO input γ(t) proposed in (8) is not a discrete-time equation since the sampling time τ can be chosen as any value theoretically. τ used in the control design in Part B also matches this instruction, which can be further indicated by the Lyapunov function in stability analysis.

Remark 7. Compared with the conventional adaptive state observers, the proposed ILO has several advantages. It is able to estimate both system states and time-varying disturbance at the same time. Additionally, persistence of excitation (PE) is not required, which is necessary for the adaptive observers to update the estimation law online.

Subtracting (8) from (7) results in the estimation error dynamics as

(9)

where

is the estimate error.

The disturbance estimation error

and an auxiliary variable d_τ are defined as follows:

(10)

and then it yields

(11)

By substituting (11) into (9), it yields

(12)

Theorem 8. Given the system dynamics in (7) with the proposed ILO designed in (8), the state estimate error is bounded if the following conditions hold:

(13)

Proof. Define the following Lyapunov function candidate:

(14)

where P is a positive definite symmetric matrix.

Based on (9) and (12), differentiating V₁ with respect to time yields

(15)

where ρ and ε are positive constants and ρ − ε = 1.

Substituting (11) into (15), we can obtain

(16)

For any Q = Q^T > 0, there exists P = P^T > 0 satisfying the following Riccati equation:

(17)

Then it yields

(18)

By using the inequality in

(19)

It follows that

(20)

namely,

(21)

where k = λ_min(Q) − 2ηλ_max(P) > 0.

If holds, the estimation error as well as the generalized disturbances is uniformly ultimately bounded (UUB) [38].

3.2. Observer Based Iterative Sliding Mode Controller Design

As to the controller design, an ILO based sliding mode controller is proposed for the output feedback course keeping control problem of the FSHV based on an iterative learning sliding surface. Before the controller design, we first make the following transformation.

By utilizing the feedback linearization method and replacing the system states with the estimated values, the system model in (2) can be rewritten as

(22)

where χ is a virtual control variable defined as

(23)

Based on the proposed ILO, the estimate of f_d(t) can be obtained as

By using

as a feedforward compensator, the virtual control can be designed as

. Then it yields

(24)

where e_d is the residual error of

and

Based on (24), the iterative learning sliding mode controller can be designed as follows.

Define a novel sliding surface with an iterative item in the following form:

(25)

where K, K_τ ∈ R^2×2 are sliding parameters to be designed.

Remark 9. According to (25), it is clear that if the time interval τ is chosen as τ = 0, the sliding surface will become , which is actually a conventional linear sliding surface. Hence, the existence of τ implies the improvement of the dynamic performance of the iterative learning sliding surface.

Let s = 0, then it yields

(26)

Define the Lyapunov function V₂ as

(27)

where Φ, Z are positive definite matrices.

Differentiating V₂ with respect to time yields

(28)

Substituting (26) into (28), we can obtain

(29)

Denote

; then (29) can be rewritten as

(30)

By appropriately tuning K, K_τ, Φ, and Z, there exists a positive definite matrix Γ such that

(31)

Then it yields

(32)

which indicates that the iterative learning sliding motion (25) is asymptotically stable. Therefore, once the system trajectory reaches the sliding surface, it can be kept at the sliding surface.

Based on the proposed sliding surface, the control law χ_s can be designed as

(33)

where α is a positive scalar.

Then the final control input u is obtained as

(34)

Therefore, the iterative learning sliding mode controller for the course keeping of the FSHV in an output feedback scheme is implemented.

4. Stability Analysis

The closed-loop stability of the observer-controller structure of system (5) is analyzed in this part.

Theorem 10. Given the system model for the course keeping control of the FSHV in (5), with the ILO proposed in (8) and the feedback linearization based iterative learning sliding mode controller in (34), uniformly ultimate boundedness can be guaranteed for the closed-loop system at the equilibrium point.

Proof. The Lyapunov function of the closed-loop system is selected as

(35)

Differentiating V₃ with respect to time, we can obtain

(36)

Based on the results of (21), (24), and (25), substituting the control law (34) into (36), we have

(37)

(38)

(39)

Together with the results of Theorem 8, if the conditions

(40)

hold, the equilibrium point of system (5) is uniformly ultimately bounded.

5. Simulation

In this section, a mathematical model of a FSHV [2, 3] is applied to validate the performance of the proposed approach. The physical parameters of the FSHV are given in Table 1.

Table 1. Model parameters of the FSHV.

Parameter	Value	SI-unit
u₀	23.15	m/s
m	2.62∗10⁵	kg
I_x	2.59∗10⁵	kgm²
I_z	1.47∗10⁷	kgm²
	0.025	m
K_p	−13.0354∗10⁵	kgm²/s
K_r	−2.4864∗10⁵	kgm²/s
K_rrϕ	−19.0883∗10⁵	kgm²/s
K_rϕϕ	12.5615∗10⁵	kgm²/s
N_p	−0.2182∗10⁷	kgm²/s
N_r	−1.3818∗10⁷	kgm²/s
N_rrϕ	0.9261∗10⁷	kgm²/s
N_rϕϕ	−1.5141∗10⁷	kgm²/s
	−1.046	kgm²/s
	5.84	kgm²/s
	0.3925	kgm²/s
	−0.2308	kgm²/s

The nominal system model with norm-bounded perturbation items is used to simulate the model uncertainties; namely,

, where

is the parameter with perturbation and p_jj is the nominal model parameter of (1). To simulate the wave disturbance, the Pierson-Moskowitz (PM) spectrum is selected as the standard wave energy spectrum [39], which can be expressed as

(41)

where A = 8.1 · 10⁻³g²,

, and H_1/3 is the significant wave height [37].

When a marine vessel is sailing in the open sea at a fixed speed, the encounter frequency is

(42)

where U is the sailing speed and β is the wave-to-course angle. So the wave energy spectrum related to the encounter frequency is

(43)

According to the strip theory and equivalent energy division method, the disturbance moments of the yaw and roll dynamics can be calculated.

To verify the effectiveness of the proposed control scheme, the following control methodologies are demonstrated for comparison.

(1)
Iterative learning observer based sliding mode controller (ILSMC): this is the observer based sliding mode control approach using iterative learning strategy proposed in the previous sections. In order to reduce the chattering phenomenon, a saturated function sat(·) is utilized instead of sgn(·). The control parameters are listed as follows:
(44)
(2)
Iterative learning observer with standard sliding mode controller (ILOSSMC): in this method, a standard sliding surface is used instead of the iterative learning sliding manifold to verify the advantage of the proposed control approach. In the ILOSSMC, K_τ = 0, and the other parameters are the same as the ILSMC.
(3)
Linear extended state observer with standard sliding mode controller (LESOSSMC): in this method, the system model is linearized by an auxiliary feedback linearization approach. Based on this approach, a linear extended state observer (LESO) is designed to estimate system states as well as the generalized disturbances. The sliding mode controller design is similar to the ILOSSMC. The LESO is designed as follows:
(45)
where x₁ is the system output, , are the estimate values of x₁, x₂, and z₃ is the extended state for the estimate of the generalized disturbances. The parameters of the LESO are selected as follows: l₁ = 54, l₂ = 189, and l₃ = 3472.

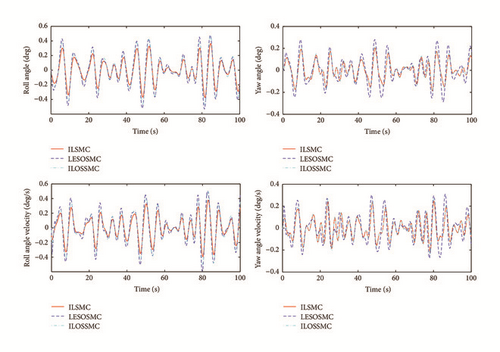
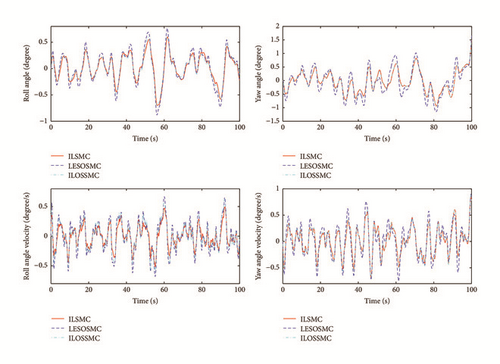
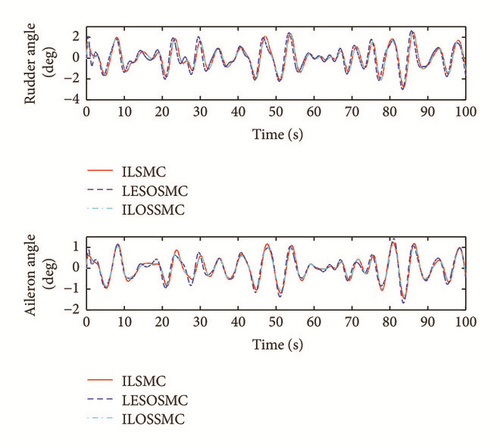
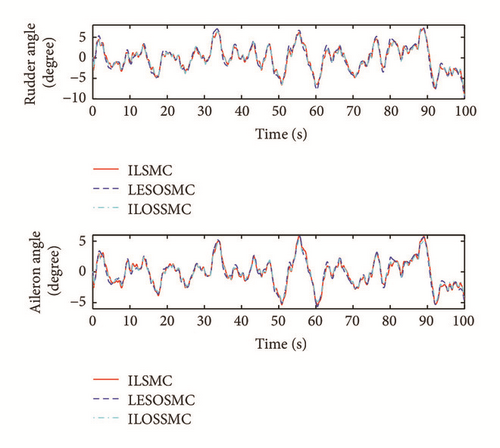
The above control schemes are tested individually for the course keeping of the FSHV in two typical cases, namely, Case 1 (sea state 3, H_1/3 = 1.5 m) and Case 2 (sea state 5, H_1/3 = 3.8 m). Figures 3 and 4 show the stabilization of roll and yaw dynamics based on three control methods on the condition H_1/3 = 1.5 m and H_1/3 = 3.8 m, respectively. The rudder angle and aileron angle of the two cases are presented in Figures 5 and 6. From Figures 3–6, we can see that based on the online iterative optimization, the stabilization performance of the ILSMC is better than that of the LESOSSMC against wave disturbances, and the system consumption of the ILSMC does not increase. Comparing the ILSMC with the ILOSSMC, we can see that the iterative learning item in the sliding manifold (25) plays an important role in the system stabilization. Utilizing the learning item, the system control can be automatically regulated according to the tendency of the system trajectory, which decreases the conservation in control design.

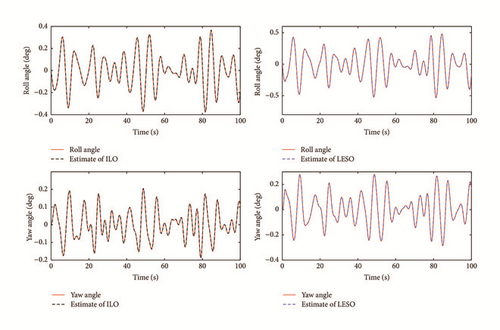
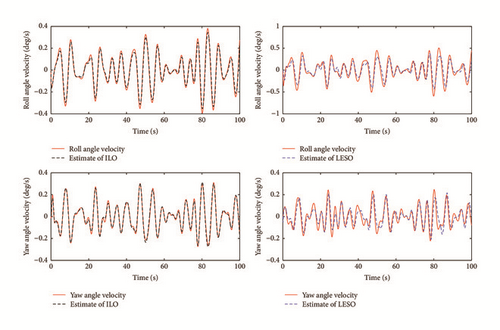
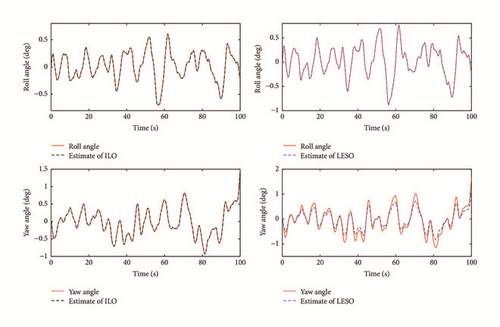
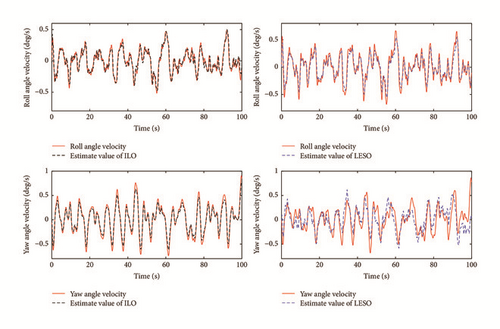
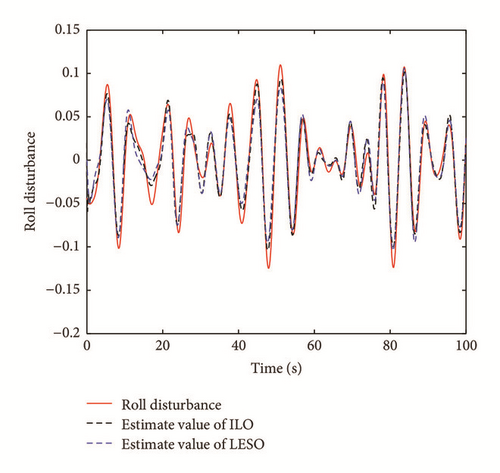
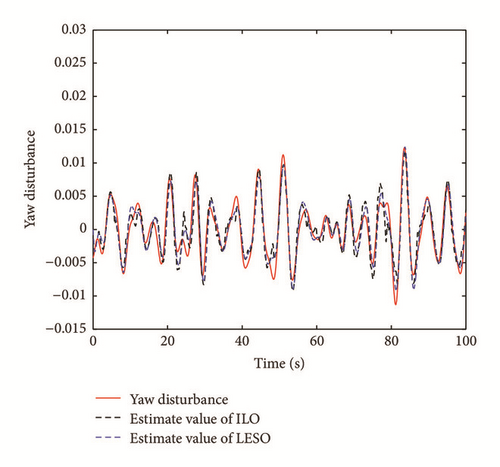
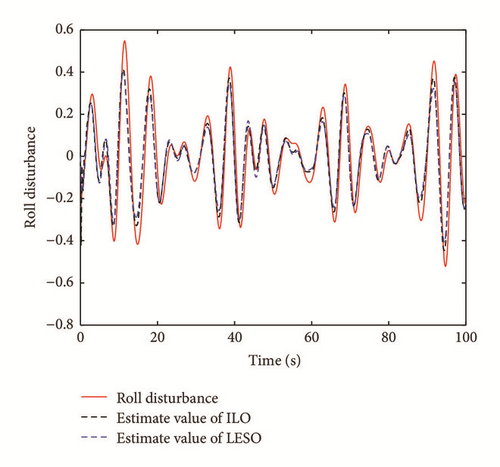
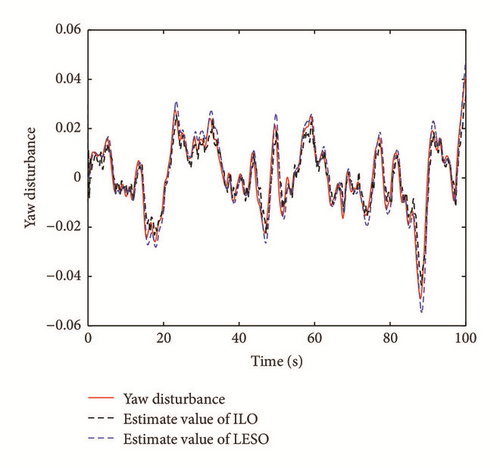
As to the state estimate, Figures 7 and 8 show the real system state and the state estimate of the ILO and the LESO in Case 1, and Figures 9 and 10 present the system estimate in Case 2. It can be shown from Figures 7–10 that the estimate accuracy of the ILO is higher than that of the LESO. Because of the high-gain character of the LESO, the peak phenomenon will occur if the observer gain selected is too large, while this problem will not happen in the ILO. Because of the design of γ(t) in the ILO, the estimating values can be updated dynamically according to the sample time τ, which enhances the state estimate precision for the system. In addition, γ(t) can detect the generalized disturbances and compensate them in the feedforward loop. The comparison of the disturbance estimate between the ILO and the LESO is illustrated in Figure 11 (Case 1) and Figure 12 (Case 2). It is illustrated that with the increase of the disturbances, the gaps in disturbances observing of the two methods become more obvious, which signifies the advantages of the ILO in severely perturbed systems. Using fixed observer gain, the ILO represents a self-adaptation property in state estimate, which achieves a better disturbance rejection performance than the LESO. The root mean square errors (RMSE) of the above state observers are listed in Table 2.

Table 2. Estimate performance comparison of the observers.

RMSE
Case 1	ILO	0.164	0.088	0.161	0.092	0.048	0.004
Case 1	LESO	0.215	0.122	0.219	0.126	0.049	0.006
Case 2	ILO	0.258	0.184	0.187	0.161	0.061	0.012
Case 2	LESO	0.317	0.298	0.258	0.214	0.063	0.013

6. Conclusion

In this paper, an output feedback control scheme is investigated for the course keeping control of the fully submerged hydrofoil vessel based on an iterative learning strategy. An iterative learning observer is illustrated for the estimation of system states as well as the generalized disturbances. Then an iterative sliding model controller is established for the attitude stabilization of the fully submerged hydrofoil vessel. Based on the ILO, the disturbances can be estimated through the inner loop, and the iterative sliding mode controller attenuates the residual error of the estimated disturbances in the outer loop. Based on Lyapunov stability theory, uniformly ultimate boundedness of the overall closed-loop system is guaranteed. With the intervention of the iterative item, performance of the transient states can be improved for both state observer and controller. Comparative simulation results illustrate that the proposed approach achieves better estimate accuracy and disturbance rejection performance. The system conservation also decreases compared with conventional approaches. In future work, time-varying sampling time is to be considered based on the time scale and frequency characteristic of the system. And the control objective for the FSHV will extend to the kinematic level with goals such as path following and trajectory tracking.

Conflicts of Interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Acknowledgments

This work is supported by National Natural Science Foundation of China under Grant 51579047.

References

1 Saito Y. and Ikebuchi T., Fully submerged hydrofoil vessel, Proceedings of the 7th Marine Dynamics Symposium on Prediction of Seakeeping Qualities of High-Speed Vessel, 1990, 107–141.
Google Scholar
2 Imamura H., Saito Y., and Asao M., Automatic control system for jetfoil, Kawasaki Technical Review. (1990) no. 107, 1–9.
Google Scholar
3 Liu S., Xu C., and Wang Y., Disturbance rejection control for the course keeping of the fully-submerged hydrofoil craft, Proceedings of the 35th Chinese Control Conference, CCC 2016, July 2016, Chengdu, China, IEEE, 747–751, https://doi.org/10.1109/ChiCC.2016.7553174, 2-s2.0-84987904286.
10.1109/ChiCC.2016.7553174
Google Scholar
4 Kim S.-H. and Yamato H., On the design of a longitudinal motion control system of a fully-submerged hydrofoil craft based on the optimal preview servo system, Ocean Engineering. (2004) 31, no. 13, 1637–1653, https://doi.org/10.1016/j.oceaneng.2004.02.004, 2-s2.0-3242669072.
10.1016/j.oceaneng.2004.02.004
Web of Science® Google Scholar
5 Do K. D. and Pan J., State- and output-feedback robust path-following controllers for underactuated ships using Serret-Frenet frame, Ocean Engineering. (2004) 31, no. 5-6, 587–613, https://doi.org/10.1016/j.oceaneng.2003.08.006, 2-s2.0-1842854533.
10.1016/j.oceaneng.2003.08.006
Web of Science® Google Scholar
6 Zhang L. J., Jia H. M., and Qi X., NNFFC-adaptive output feedback trajectory tracking control for a surface ship at high speed, Ocean Engineering. (2011) 38, no. 13, 1430–1438, https://doi.org/10.1016/j.oceaneng.2011.07.006, 2-s2.0-80052266674.
10.1016/j.oceaneng.2011.07.006
CAS Web of Science® Google Scholar
7 Kim S.-H. and Yamato H., An experimental study of the longitudinal motion control of a fully submerged hydrofoil model in following seas, Ocean Engineering. (2004) 31, no. 5-6, 523–537, 2-s2.0-1842854537, https://doi.org/10.1016/j.oceaneng.2003.10.003.
10.1016/j.oceaneng.2003.10.003
Web of Science® Google Scholar
8 Rosales A. and Boiko I., Disturbance attenuation for systems with second-order sliding modes via linear compensators, IET Control Theory & Applications. (2015) 9, no. 4, 526–537, https://doi.org/10.1049/iet-cta.2014.0252, MR3328476.
10.1049/iet-cta.2014.0252
Web of Science® Google Scholar
9 Feng Y., Han F., and Yu X., Chattering free full-order sliding-mode control, Automatica. A Journal of IFAC, the International Federation of Automatic Control. (2014) 50, no. 4, 1310–1314, https://doi.org/10.1016/j.automatica.2014.01.004, MR3191406, Zbl1298.93104, 2-s2.0-84898889102.
10.1016/j.automatica.2014.01.004
Web of Science® Google Scholar
10 Sánchez-Torres J. D., Navarrete-Guzman A., Rubio-Astorga G., and Loukianov A. G., High order integral nested sliding mode control, Proceedings of the 13th International Workshop on Variable Structure Systems, VSS 2014, July 2014, Nantes, France, IEEE, https://doi.org/10.1109/VSS.2014.6881094, 2-s2.0-84906815234.
10.1109/VSS.2014.6881094
Google Scholar
11 Ji S.-W., Bui V. P., Balachandran B., and Kim Y.-B., Robust control allocation design for marine vessel, Ocean Engineering. (2013) 63, 105–111, 2-s2.0-84875140638, https://doi.org/10.1016/j.oceaneng.2013.02.004.
10.1016/j.oceaneng.2013.02.004
Web of Science® Google Scholar
12 Du J., Yang Y., Wang D., and Guo C., A robust adaptive neural networks controller for maritime dynamic positioning system, Neurocomputing. (2013) 110, 128–136, 2-s2.0-84876101957, https://doi.org/10.1016/j.neucom.2012.11.027.
10.1016/j.neucom.2012.11.027
Web of Science® Google Scholar
13 Kahveci N. E. and Ioannou P. A., Adaptive steering control for uncertain ship dynamics and stability analysis, Automatica. A Journal of IFAC, the International Federation of Automatic Control. (2013) 49, no. 3, 685–697, https://doi.org/10.1016/j.automatica.2012.11.026, MR3027525, Zbl1267.93086, 2-s2.0-84875209816.
10.1016/j.automatica.2012.11.026
Web of Science® Google Scholar
14 Patre P. M., MacKunis W., Johnson M., and Dixon W. E., Composite adaptive control for Euler-Lagrange systems with additive disturbances, Automatica. A Journal of IFAC, the International Federation of Automatic Control. (2010) 46, no. 1, 140–147, https://doi.org/10.1016/j.automatica.2009.10.017, MR2578283, Zbl1213.93104, 2-s2.0-73049111114.
10.1016/j.automatica.2009.10.017
Web of Science® Google Scholar
15 Hammouri H., Bornard G., and Busawon K., High gain observer for structured multi-output nonlinear systems, Institute of Electrical and Electronics Engineers. Transactions on Automatic Control. (2010) 55, no. 4, 987–992, https://doi.org/10.1109/TAC.2010.2041614, MR2654442, 2-s2.0-77950836616.
10.1109/TAC.2010.2041614
Google Scholar
16 Wang L. and Su J., Robust Disturbance Rejection Control for Attitude Tracking of an Aircraft, IEEE Transactions on Control Systems Technology. (2015) 23, no. 6, 2361–2368, 2-s2.0-84923250036, https://doi.org/10.1109/TCST.2015.2398811.
10.1109/TCST.2015.2398811
Web of Science® Google Scholar
17 Ginoya D., Shendge P. D., and Phadke S. B., Sliding mode control for mismatched uncertain systems using an extended disturbance observer, IEEE Transactions on Industrial Electronics. (2014) 61, no. 4, 1983–1992, 2-s2.0-84887286651, https://doi.org/10.1109/TIE.2013.2271597.
10.1109/TIE.2013.2271597
Web of Science® Google Scholar
18 Mohammadi A., Tavakoli M., Marquez H. J., and Hashemzadeh F., Nonlinear disturbance observer design for robotic manipulators, Control Engineering Practice. (2013) 21, no. 3, 253–267, https://doi.org/10.1016/j.conengprac.2012.10.008, 2-s2.0-84872391084.
10.1016/j.conengprac.2012.10.008
Web of Science® Google Scholar
19 Sun H., Li S., Yang J., and Guo L., Non-linear disturbance observer-based back-stepping control for airbreathing hypersonic vehicles with mismatched disturbances, IET Control Theory and Applications. (2014) 8, no. 17, 1852–1865, 2-s2.0-84917741316.
10.1049/iet-cta.2013.0821
Web of Science® Google Scholar
20 Xingling S. and Honglun W., Back-stepping active disturbance rejection control design for integrated missile guidance and control system via reduced-order ESO, ISA Transactions. (2015) 57, 10–22, https://doi.org/10.1016/j.isatra.2015.02.013.
10.1016/j.isatra.2015.02.013
PubMed Web of Science® Google Scholar
21 Chen W. H., Nonlinear Disturbance Observer-Enhanced Dynamic Inversion Control of Missiles, Journal of Guidance Control & Dynamics. (2012) 26, no. 1, 161–166.
10.2514/2.5027
Google Scholar
22 Wang J., Li S., Yang J., Wu B., and Li Q., Extended state observer-based sliding mode control for PWM-based DC-DC buck power converter systems with mismatched disturbances, IET Control Theory and Applications. (2015) 9, no. 4, 579–586, 2-s2.0-84924510594, https://doi.org/10.1049/iet-cta.2014.0220.
10.1049/iet-cta.2014.0220
CAS Web of Science® Google Scholar
23 Wang C., Li X., Guo L., and Li Y. W., A nonlinear-disturbance-observer-based DC-Bus voltage control for a hybrid AC/DC microgrid, IEEE Transactions on Power Electronics. (2014) 29, no. 11, 6162–6177, https://doi.org/10.1109/tpel.2013.2297376, 2-s2.0-84904438030.
10.1109/TPEL.2013.2297376
Web of Science® Google Scholar
24 Ekramian M., Sheikholeslam F., Hosseinnia S., and Yazdanpanah M. J., Adaptive state observer for Lipschitz nonlinear systems, Systems and Control Letters. (2013) 62, no. 4, 319–323, 2-s2.0-84874618616.
10.1016/j.sysconle.2013.01.002
Web of Science® Google Scholar
25 Li Y. and Tong S., Adaptive Fuzzy Output-Feedback Stabilization Control for a Class of Switched Nonstrict-Feedback Nonlinear Systems, IEEE Transactions on Cybernetics. (2016) 2-s2.0-84960969283, https://doi.org/10.1109/TCYB.2016.2536628.
10.1109/TCYB.2016.2536628
Google Scholar
26 Tong S., Li Y., and Sui S., Adaptive fuzzy tracking control design for uncertain non-strict feedback nonlinear systems, IEEE Transactions on Fuzzy Systems. (2016) 24, no. 6, 1441–1454, https://doi.org/10.1109/tfuzz.2016.2540058.
10.1109/TFUZZ.2016.2540058
Web of Science® Google Scholar
27 Li Y., Tong S., Liu L., and Feng G., Adaptive output-feedback control design with prescribed performance for switched nonlinear systems, Automatica. A Journal of IFAC, the International Federation of Automatic Control. (2017) 80, 225–231, https://doi.org/10.1016/j.automatica.2017.02.005, MR3638076.
10.1016/j.automatica.2017.02.005
Web of Science® Google Scholar
28 Tong S., Li Y., and Sui S., Adaptive Fuzzy Output Feedback Control for Switched Nonstrict-Feedback Nonlinear Systems With Input Nonlinearities, IEEE Transactions on Fuzzy Systems. (2016) 24, no. 6, 1426–1440, https://doi.org/10.1109/TFUZZ.2016.2516587.
10.1109/TFUZZ.2016.2516587
Web of Science® Google Scholar
29 Sakamoto N., Rehák B., and Ueno K., Nonlinear Luenberger observer design via invariant manifold computation, IFAC Proceedings Volumes. (2014) 47, no. 3, 37–42, 2-s2.0-84929742273.
10.3182/20140824-6-ZA-1003.01103
Google Scholar
30 Alessandri A. and Rossi A., Increasing-gain observers for nonlinear systems: stability and design, Automatica. A Journal of IFAC, the International Federation of Automatic Control. (2015) 57, 180–188, https://doi.org/10.1016/j.automatica.2015.04.017, MR3350689, 2-s2.0-84930062541.
10.1016/j.automatica.2015.04.017
Web of Science® Google Scholar
31 Mu C. and Sun C., A new finite time convergence condition for super-twisting observer based on Lyapunov analysis, Asian Journal of Control. (2015) 17, no. 3, 1050–1060, https://doi.org/10.1002/asjc.952, MR3349229, 2-s2.0-84929175777.
10.1002/asjc.952
Web of Science® Google Scholar
32 Daly J. M. and Wang D. W. L., Output feedback sliding mode control in the presence of unknown disturbances, Systems and Control Letters. (2009) 58, no. 3, 188–193, https://doi.org/10.1016/j.sysconle.2008.10.007, 2-s2.0-58249142510.
10.1016/j.sysconle.2008.10.007
Web of Science® Google Scholar
33 Grip H. v., Saberi A., and Johansen T. A., Observers for interconnected nonlinear and linear systems, Automatica. A Journal of IFAC, the International Federation of Automatic Control. (2012) 48, no. 7, 1339–1346, https://doi.org/10.1016/j.automatica.2012.04.008, MR2942321, 2-s2.0-84862907269.
10.1016/j.automatica.2012.04.008
Web of Science® Google Scholar
34 Ghanes M., De Leon J., and Barbot J.-P., Observer design for nonlinear systems under unknown time-varying delays, Institute of Electrical and Electronics Engineers. Transactions on Automatic Control. (2013) 58, no. 6, 1529–1534, https://doi.org/10.1109/TAC.2012.2225554, MR3065135, 2-s2.0-84878314971.
10.1109/TAC.2012.2225554
Google Scholar
35 Ekramian M., Sheikholeslam F., Hosseinnia S., and Yazdanpanah M. J., Adaptive state observer for Lipschitz nonlinear systems, Systems and Control Letters. (2013) 62, no. 4, 319–323, https://doi.org/10.1016/j.sysconle.2013.01.002, 2-s2.0-84874618616.
10.1016/j.sysconle.2013.01.002
Web of Science® Google Scholar
36 Holakooie M. H., Ojaghi M., and Taheri A., Full-order Luenberger observer based on fuzzy-logic control for sensorless field-oriented control of a single-sided linear induction motor, ISA Transactions. (2016) 60, 96–108, 2-s2.0-84959486882, https://doi.org/10.1016/j.isatra.2015.11.022.
10.1016/j.isatra.2015.11.022
PubMed Web of Science® Google Scholar
37 Fossen T. I., Handbook of Marine Craft Hydrodynamics and Motion Control, 2011, John Wiley & Sons, West Sussex, UK, https://doi.org/10.1002/9781119994138.
10.1002/9781119994138
Google Scholar
38 Khalil H. K., Nonlinear Systems, 2002, 3rd edition, Prentice-Hall, Inc, Upper Saddle River, NJ, USA.
Web of Science® Google Scholar
39 Panneer Selvam R. P. and Bhattacharyya S. K., System identification of a coupled two DOF moored floating body in random ocean waves, Journal of Offshore Mechanics and Arctic Engineering. (2006) 128, no. 3, 191–202, https://doi.org/10.1115/1.2199557, 2-s2.0-33748670048.
10.1115/1.2199557
Web of Science® Google Scholar

Citing Literature

All articles

Robust Course Keeping Control of a Fully Submerged Hydrofoil Vessel without Velocity Measurement: An Iterative Learning Approach

Abstract

1. Introduction

2. Problem Formulation

3. Output Feedback Control Design of the FSHV

3.1. Iterative Learning Observer Design

3.2. Observer Based Iterative Sliding Mode Controller Design

4. Stability Analysis

5. Simulation

6. Conclusion

Conflicts of Interest

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Robust Course Keeping Control of a Fully Submerged Hydrofoil Vessel without Velocity Measurement: An Iterative Learning Approach

Abstract

1. Introduction

2. Problem Formulation

3. Output Feedback Control Design of the FSHV

3.1. Iterative Learning Observer Design

3.2. Observer Based Iterative Sliding Mode Controller Design

4. Stability Analysis

5. Simulation

6. Conclusion

Conflicts of Interest

Acknowledgments

References

Citing Literature

Figures

References

Related

Information