On the Resistance-Harary Index of Graphs Given Cut Edges

Lemma 1 (see [1], [13], [14].)Let x be a cut vertex of a graph G, and let a and b be vertices in different components of G − x. Then

Lemma 2. The functions f₁(x) = x/(2/x + m) − (x − 1)/(2/(x − 1) + m) for x ≥ 2 and m > 0 and f₂(x) = x/(2/x + A)(2/x + B) for x > 1 and A > 0, B > 0 are strictly increasing.

Proof. By simple calculation,

Since x ≥ 2 and m > 0, $$ is the derivative of function f₁(x) on x. Obviously, f₁(x) is a strictly increasing function for x ≥ 2 and m > 0.

Similarly, we prove that the function f₂(x) = x/(2/x + A)(2/x + B) for x > 1 and A > 0, B > 0 is also an increasing function. We finally obtain the result.

Lemma 3. Let G be a connected graph with at least three vertices. If G is not isomorphic to K_n, Let G^∗ = G + e, and then RH(G^∗) > RH(G).

Proof. Suppose that G is not a complete graph. Then there exists a pair of vertices v_i and v_j in G such that $$.

Let G^∗ = G + v_iv_j, we have

We only to prove that $$; the proof of $$ for (r, s)≠(i, j) is similar. We distinguish the following two cases.

Case  1. v_i and v_j are vertices of cycle C_g in G, where g is the length of C_g.

Let d₁(v_i, v_j) and d₂(v_i, v_j) be distance between v_i and v_j in the cycle C_g, respectively. By the definition of resistance, we have

That is to say, $$.

Case  2. v_i and v_j are not vertices in any cycle of G.

In this case, we have

This completes the proof.

Lemma 4. Let xy ∈ E(G) be a cut edge in G, and let G₁ and G₂ be the two components of G − xy. Suppose further that x ∈ V(G₁) and y ∈ V(G₂), and then $$.

Proof. By the definition of Resistance-Harary index and by Lemma 1, we have

This completes the proof.

Lemma 5. Let G and G^′ be the graphs in Figure 1, where G₀ is a complete graph, and then RH(G) ≤ RH(G^′), with equality if and only if x₁ = x₂ = ⋯ = x_r.

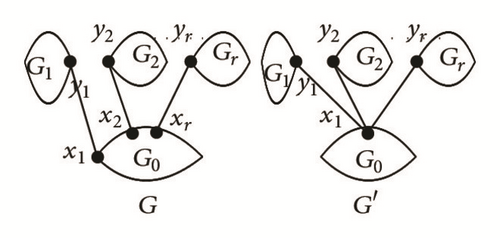
Proof. From the definition of the Resistance-Harary index and Lemma 4, we have

Similarly, Since G₀ is a complete graph, $$ for 1 ≤ i ≤ r. And with equality if and only if $$; that is, x₁ = x₂ = ⋯ = x_r. This completes the proof.

Lemma 6. Let G and G^′ be the graphs depicted in Figure 2, where G₂ and G₃ are all complete graphs. Let n_i be the number of vertices of G_i, where i = 2,3. If n₃ > n₂ and V(G₄) may be an empty set, then RH(G^′) > RH(G).

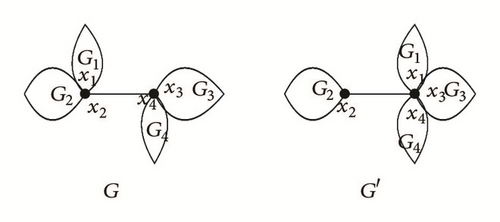
Proof. By the definition of the Resistance-Harary index and Lemmas 1 and 4, we have

Since G₂ and G₃ are all complete graphs, for any two vertices x, y ∈ V(G_i), we have $$, where i = 2, 3. Similarly, we have We just need to prove that

In fact,

In the following, we just need to prove that the fraction of ∇₁ is greater than zero. Denote ∇₂ to be the fraction of ∇₁; in fact,

Since n₃ > n₂, RH(G^′) > RH(G). This completes the proof.

Lemma 7. Let n and n₀, n₁, …, n_k  (k ≥ 1) be positive integers such that n₀ ≥ n₁ ≥ ⋯≥n_k, n₁ > 1, and n₀ + n₁ + ⋯+n_k = n. Let $$ (see Figure 3) and $$. Then RH(G^′) > RH(G).

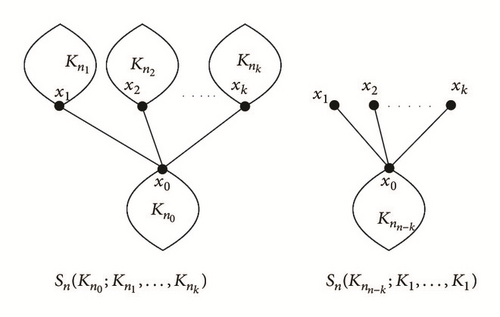
Proof. By direct calculation, we have

Similarly, we can deduce the value of RH(G^′). Then In order to prove that the result RH(G^′) > RH(G), we distinguish three steps in the following. Denote

Obviously, △₂ > 0. In the following, we first prove that △₁ > 0. By direct calculation, we have

(since n₀ ≥ n₁ > 1). Secondly, we will prove that △₃ > 0. where the second inequality is due to the fact that where A = 2/n_i + 1, B = 2/n_i + 2, and the function f(x) = x/(2/x + A)(2/x + B) is an increasing function, and then By Lemma 2, the last inequality is due to the fact the function f₂(x) = x/(2/x + A) − (x − 1)/(2/(x − 1) + A) for x ≥ 2 and 0 < A ≤ 3 is an increasing function.

By combination with above discussion, we have RH(G^′) > RH(G), which finishes the proof of Lemma 7.

Corollary 8. Suppose that $$ is defined as above and n₀ ≥ n₁ ≥ n₂ ≥ ⋯≥n_k, the value of $$ reaches its maximum value at n₀ = n − k and n₁ = n₂ = ⋯ = n_k = 1.

Theorem 9. If G is a connected graph with k cut edges and n vertices, then

with equality if and only if G≅S_n(K_n−k; K₁, K₁, …, K₁) (see Figure 3).

Proof. To determine the maximum Resistance-Harary index of the graph, we select such a connected graph so that it cut off all the cut edges for a complete graph by Lemma 3. Moreover, we can further choose $$ by Lemmas 5 and 6, and let $$, n₀ = max⁡{n₀, n₁, …, n_k}. From the definition of the Resistance-Harary index and Lemma 4, we have

By Lemma 7 and Corollary 8, we know that the equality holds if and only if n₀ = n − k, n₁ = n₂ = ⋯ = n_k = 1; that is, G≅S_n(K_n−k; K₁, …, K₁). This completes the result.

Corollary 10. If T is a tree with n vertices, then RH(G) ≤ (n² + n − 2)/4, with equality if and only if T≅S_n.

Proof. Since T is a tree with n vertices, it has n − 1 cut edges, and RH(G) ≤ (n² + n − 2)/4 with equality if and only if T≅S_n by Theorem 9. This completes the result.