During the last decade, tremendous focus has been given to sustainable logistics practices to overcome environmental concerns of business practices. Since transportation is a prominent area of logistics, a new area of literature known as Green Transportation and Green Vehicle Routing has emerged. Vehicle Routing Problem (VRP) has been a very active area of the literature with contribution from many researchers over the last three decades. With the computational constraints of solving VRP which is NP-hard, metaheuristics have been applied successfully to solve VRPs in the recent past. This is a threefold study. First, it critically reviews the current literature on EMVRP and the use of metaheuristics as a solution approach. Second, the study implements a genetic algorithm (GA) to solve the EMVRP formulation using the benchmark instances listed on the repository of CVRPLib. Finally, the GA developed in Phase 2 was enhanced through machine learning techniques to tune its parameters. The study reveals that, by identifying the underlying characteristics of data, a particular GA can be tuned significantly to outperform any generic GA with competitive computational times. The scrutiny identifies several knowledge gaps where new methodologies can be developed to solve the EMVRPs and develops propositions for future research.

1. Introduction

Background of Research. Vehicle Routing Problem (VRP) can be described as the problem of finding optimal routes for delivery or collection from one to many depots to many customers who are geographically distributed. This problem has been the core for many operations research problems and has many variations. Later, with the focus on sustainable business practices, a novel category of VRP has emerged, known as Green VRP. In this category, the objectives are different from original VRP where it minimizes the travelled distance ultimately, thus reducing the cost. However, GVRP attempts to minimize the impact on environment of routing using different approaches [1]. Energy Minimizing VRP (EMVRP) has been developed to minimize the energy consumption of a fleet while serving all the customers. It has been identified that energy consumption has a direct impact on carbon dioxide emission.

Metaheuristics are used for combinatorial optimization in which an optimal solution is sought over a discrete search space. VRP is one of the most known NP-hard problems; thus, metaheuristics have been widely used to find near-optimal solutions for VRP problems [2].

Machine learning is a subfield of computer science that evolved from the study of pattern recognition and computational learning theory in artificial intelligence. Machine learning explores the construction and study of algorithms that can learn from and make predictions on data. In this research, the intention is to use machine learning to tune the developed metaheuristics to solve the formulated routing problem [3]. The overall objective of this study is to develop a set of genetic algorithms to solve the EMVRP and apply machine learning techniques to tune the developed algorithms to enhance the quality of the solutions. Energy Minimizing VRP has been formulated by Kara et al. [1] with the objective of minimizing energy consumption while serving a distributed set of customers. Though it minimizes the energy consumption, the calculated reduction of carbon dioxide emission has not been calculated; thus, the environmental sustainability of EMVRP has not been stated in the original paper. The study has used CPLEX® for solving moderate sized problems and the computational times were not promising. It is therefore necessary to develop efficient solution procedures for the EMVRP and in this study the authors implement genetic algorithms (GAs) for the genetic EMVRP formulation. The aforementioned GA was enhanced through machine learning techniques to tune its parameters based on the underlying characteristics of the data being used. In the book Tuning Metaheuristics by Birattari [3], it has been mentioned that tuning is crucial to metaheuristic optimization both in academic viewpoint and for practical applications. Nevertheless, relatively less research has been devoted to the issue and shows that the problem of tuning a metaheuristic can be described and solved as a machine learning problem. To the authors’ knowledge, this will be the first instance of machine learning being used as a mechanism to tune the domain of VRP.

2. Literature Review

2.1. Vehicle Routing Problem

Vehicle Routing Problem (VRP) can be described as the problem of finding optimal routes for delivery or collection from one to many depots to many customers who are geographically distributed. VRP is at the core of a huge number of practical applications in the area of transportation. It is one of the most studied classes of problems in operations research (OR) according to Gendreau et al. [4]. The list of variants according to a recent survey by Lin et al. [5] can be classified as Capacitated VRP (CVRP), Time Dependent VRP (TDVRP), Pickup and Delivery Problem (PDP), Multidepot VRP (MDVRP), Stochastic VRP (SVRP), Location Routing Problem (LRP), Periodic VRP (PVRP), Dynamic VRP (DVRP), Inventory Routing Problem (IRP), Fleet Size and Mix Vehicle Routing Problem (FSMVRP), Generalized VRP, Multicompartment VRP (MCVRP), Site Dependent VRP, Split Delivery VRP (SDVRP), Fuzzy VRP, Open VRP (OVRP), VRP with Loading Constraints (VRPLC), and Multiechelon VRP (MEVRP).

2.2. Green VRP

Green Logistics has recently received a lot of interest from governments and business organizations. The main reason behind this is that the current logistics practices are not sustainable in the long term and sometimes in the literature there are instances where the improved performance in terms of economic performance has caused a decrease in environmental performance. A classic example can be found in the study done by Yazan et al. [6] where they reengineered the supply chain, but, however, their reengineering outcomes seem to have been unsuccessful with regard to CO₂ emission, since CO₂ emission has been increased after the study, and this shows reengineering failure in environmental sense, although the economic performance has been increased by reengineering the system. With these reasons, the focus is automatically given to sustainable transportation practice which is generally known as Green Transportation. Björklund [7] defines “Green Transportation” as “transportation service that has a lesser or reduced negative impact on health and natural environment when compared with competing transportation services that serve the same purpose.” Under this category, a subcategory has been defined as “Green Vehicle Routing Problems” and they are characterized by the objective of harmonizing the environmental and economic costs by implementing effective routes to meet the environmental concerns and financial indexes [5]. The importance of Green VRP is characterized mainly by CO₂ emission by vehicles since they are one of the prime consumers of petroleum products. The sector contributes to 15% of overall greenhouse gas (GHG) emissions and 23% of overall CO₂ emissions, which is the highest found GHG [8]. The different variants of Green VRP have been introduced to the literature which have various objectives to support sustainable VRP. Those can be listed as Pollution Routing Problem (PRP), Green Vehicle Routing Problem (GVRP), and VRP in Reverse Logistics (VRPRL) [5].

2.3. Energy Minimizing Vehicle Routing Problem

Under the GVRP aimed problems, one problem introduced in 2007 by Kara et al. [1] is Energy Minimizing VRP (EMVRP). EMVRP has been identified in the survey by Lin et al. [5] under the category of GVRP. The objective of EMVRP is to reduce the energy consumption and energy has been justified to be the product of distance travelled by the load of the vehicle. Concretely, EMVRP aims at minimizing the sum of the product of load and distance for each arc. However, in the original paper, the authors have not justified the CO₂ emission reduction of EMVRP. Furthermore, the problem has been solved using CPLEX 8.0 for small sized instances and it is mentioned that the CPU times over moderate sized problems have not been optimized. Thus, this raises the need for developing efficient heuristics for solving moderate and large instances.

EMVRP is mathematically formulated first by Kara at el. [1] as in the following:

Objective function is
()
Constraints are as follows:
()

()

()

()

()

()

The cost of traversing an arc (i, j) is the product of the distance between the nodes i and j and weight on this arc. Constraints (2) and (3) ensure that m vehicles are used. Constraints (4) and (5) are the degree constraints for each node. Constraint (6) is the classical conservation of flow equation balancing inflow and outflow of each node, which also prohibits any illegal subtours. Constraint (7) initializes the flow on the first arc of each route; the cost structure of the problem necessitates such initialization. Capacity restrictions are considered and force y_ij to zero when the arc (i, j) is not on any route. Then, the constraint produces lower bounds for the flow on any arc.

2.4. Metaheuristics for Solving VRP

Metaheuristics are categories of heuristics used for solving optimization problems, mostly NP-hard problems, which cannot be optimally solved within feasible time. Lenstra and Kan [9] have shown that all the Vehicle Routing Problems are NP-hard and cannot be solved in polynomial time. In the literature, there are many instances where metaheuristics have been applied to solve VRP. Among them, the most applied path-based and population-based metaheuristics can be selected using the categorized bibliography done by Gendreau et al. [4].

2.4.1. Genetic Algorithm (GA)

Genetic algorithms (GAs) are adaptive methods which may be used to solve a wide variety of optimization problems. They are based on the genetic processes of biological organisms. Over many generations, natural populations evolve according to the principles of natural selection and “survival of the fittest.” By mimicking this process, genetic algorithms are able to “evolve” solutions to real world problems, if they have been suitably encoded. The basic principles of GAs were first laid down rigorously by Holland [10]. GA is more applicable for solving an optimization problem where the optimum result is derived from a large random dataset like the scenario in the research problem.

2.5. Machine Learning for Metaheuristics

Machine learning is an area of computer science that evolved from the study of pattern recognition and computational learning theory in artificial intelligence. It explores the construction and study of algorithms that can learn from and make predictions on data. When metaheuristics are developed, the algorithms can be tuned for better performance (Birattari [3]). Each metaheuristic has already set parameters that have to be initialized before the execution of the algorithm. The metaheuristics adaptation requires the adjustment of these parameters according to the problem at hand. This is known as parameter tuning. An appropriate initial parameter setting has a noteworthy impact on the solving progress, such as the exploitation or exploration rate of the search space, and therefore the quality of the solution [11]. Tuning metaheuristics using machine learning techniques is a novel approach and there is not much literature on the area.

3. Methodology

3.1. Research Approach

In the first phase of the study, Green VRP methodologies will be systematically reviewed to identify important characteristics of problem solving methodologies [12]. In the second phase of the study, GA-based metaheuristics are developed to solve the routes which minimize the energy consumption of a vehicle fleet while serving a set of customers. In the third phase, the applicability of machine learning techniques for parameter tuning of metaheuristics will be tested (Figure 1).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Flow diagram of the research study.

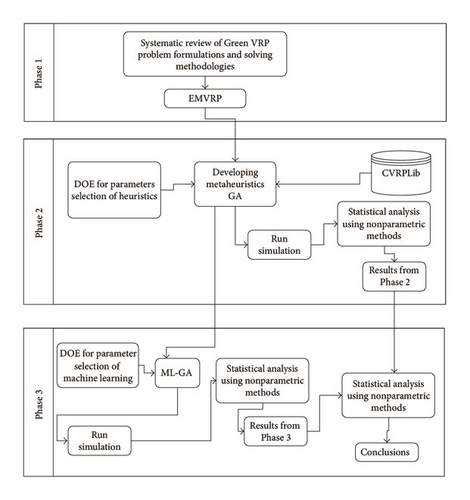
Phase 1: Systematic Review of the Literature. During this phase, a thorough review of the literature on the Green VRP problem formulations and solving methodologies was carried out. The knowledge gathered from the systematic review is intended to be used for identifying and justifying the metaheuristics to be used in solving the EMVRP.

Phase 2: Development of the GA. With the knowledge gathered from Phase 1, a genetic algorithm will be developed to solve the EMVRP. Design of experiment (DOE) will be carried out to identify the parameters and the levels for each parameter to reduce the bias. The data for the algorithms will be obtained from CVRPLib [13], an online benchmark repository of VRP instances. CVRPLib contains data that is prominently used in VRP literature with number of cities or customers that request goods to be delivered to them and the location and the size of the demand.

Phase 3: Development of the Parameter Tuned GA Using Machine Learning Techniques. The GA’s parameters will be tuned using clustering techniques based on the inherent characteristics of the data being used. The tuned GA will be compared with results from untuned GA from Phase 2. Recommendations will be drawn for using machine learning as a mechanism for parameter tuning within the context of VRP.

3.2. Data Collection

The data required for the execution of algorithms will be acquired from CVRPLib: a Vehicle Routing Problem library available online at http://vrp.atd-lab.inf.puc-rio.br/index.php/en/. This is a prominently used library used in many research studies found in the literature. These data files include collection of cities to be served with x and y coordinates, required demand for each city, and the capacity of the vehicle.

3.3. Parameter Tuning Using Machine Learning

Tuning is crucial for metaheuristic optimization from both academic and practitioners’ standpoint. Nevertheless, relatively less research has been devoted to the issue. Using the machine learning perspective, it is possible to give a formal definition to tuning of an algorithm.

4. Implementation

4.1. Problem Definition

In this section, the problem formulation of EMVRP has been described. The idea of EMVRP is stated in the study by Kara et al. [1]. Some important assumptions of this problem formulation are as follows:

(1)
A vehicle can only carry a load which is less than its capacity.
(2)
When loading a vehicle, the cumulative demand required by the cities that the particular vehicle will serve needs to be considered. This is important because if not, a vehicle might bring back the left carriage in its return trip back to the depot.
(3)
There is only one depot.
(4)
The demands and capacities are measured using the same measurement.
(5)
The weight of the vehicle is not considered since it will be the same over the fleet.

Figure 2 illustrates the above statements in a diagram.

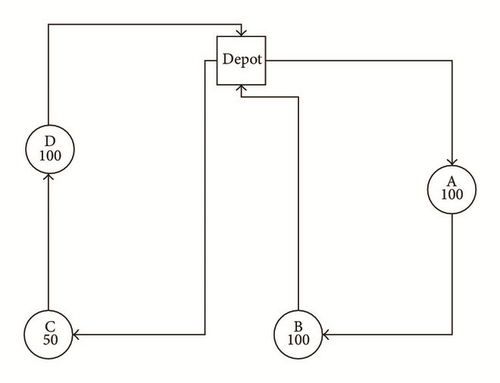
A, B, C, and D are cities that need to be served with demands of 100, 100, 50, and 100, respectively. The maximum capacity of the vehicle is 200. In the first trip (or first vehicle) which will serve A and B, the vehicle will be loaded with 200 considering demands of A and B and after serving it will return back to the depot. And in the second trip (or second vehicle), it will be loaded with only 150 considering that it has to serve C and B where cumulative demand is 150 and after serving it will return back to the depot.

4.2. The Proposed GA

The implementation of the GA uses a fully object oriented design as there are three models: city, tour, and population. The implementation of GA is shown in Algorithm 1.

Algorithm 1: Overview of basic genetic algorithm developed for the EMVRP.

Input
Read list of cities to be served with demands {city₁, city₂, …, city} from CVRP Lib file
Read vehicle capacity from text file
Population size (p)
Number of generations (n)
//Initialization
Create a tour with a random order of cities
Do this for p times to create a population
Get the best tour from the population
Save as the elite
initial energy = energy consumption of the fittest tour in first population
//Genetic algorithm
//Run for n times
Loop1{
//Run for p times
Loop2{
//Tournament selection
Select a random set of tours from the population
Get the fittest and return
//Crossover
Parent1 = tournament selection ()
Parent2 = tournament selection ()
child = Crossover (Parent1, Parent2)
//Mutation
Swap random two cities in the child
}endLoop2
//New population is created
Get the fittest
Replace previous elite if fittest is better than elite
}endLoop1
Get the elite
Final energy = energy consumption of elite
Reduction of energy = (initial energy − final energy)/initial energy ∗ 100%
Print “Reduction of energy”

4.3. Parameter Tuning of Metaheuristics Using Machine Learning

GAs need to be parameter tuned for better performance [3]. The main parameters considered in this study are mutation rate, size of the population, and number of generations. Larger sizes of the population and number of generations are deemed to yield better results as this will increase the scope of the search paradigm. However, the optimum setting for the rate of mutation cannot be identified without a scientific approach. In this study, k-means clustering algorithm from the machine learning literature has been used as a mechanism to tune the developed metaheuristics. k-means is one of the widely used unsupervised learning algorithms which solves the well-known clustering problem. For this purpose, a customized k-means clustering algorithm has been developed to read the data files from the CVRPLib and cluster them using the total accumulated demand of the cities and total number of cities to be served. Then, different mutation rates have been applied for different clusters of the data files and the energy minimization percentages are calculated. The hypothesis is as follows: different mutation rates work better on different clusters of CVRPLib. Detailed description of this experiment is elaborated in the next section along with the DOE.

5. Results

As mentioned in a previous section, the data for the experiment is taken from CVRPLib. In particular, the dataset used is from Uchoa et al. [13]. This repository contains 100 data files with the number of cities and various demands required by each city. All the experiments are carried out using a single computer with the following features and configurations.

Computational Specification of the Computer

Processor: Intel® Core™ i5-4200 CPU @ 2.50 GHz
Installed memory (RAM): 4.00 GB
System type: 64-bit operating system, x64-based processor
Pen and touch: No pen or touch input available for this display

To analyze the performance of GA, the experiment has been designed for the selected 100 data files (Table 1).

Table 1. Design of experiment (DOE) for the genetic algorithm.

Selected parameter	Values
Mutation rates	0.0010, 0.0025, 0.0050, 0.0075, 0.0100
Size of the population	50
Size of the generations	100 and 1000
Replications	5 per one mutation rate, population size, and number of generations

Note that these mutation rates, size of the population, and number of generations are the most widely used values found in the literature. The outcome of GA is energy reduction percentage compared to initial energy consumption of the tour. This is calculated as

()

5.1. Analysis of Results of the Developed GA for EMVRP

As depicted in Table 2 using any mutation rate with number of generations = 100, the energy reduction percentage is greater than 20%. The best energy reduction is achieved when the mutation rate is at 0.0025. The average computational time taken for all the 100 files is shown in Table 2.

Table 2. Results of the genetic algorithm.

Selected parameter	Value for the parameter of the genetic algorithm
Size of the population	50
Size of the generations	100					1000
Mutation rates	0.001	0.0025	0.005	0.0075	0.01	0.001	0.0025	0.0050	0.0075	0.01
Average energy reduction percentage (%)	26.64	26.70	24.54	22.54	21.42	52.98^∗	50.04	42.95	37.60	34.04
Average computational time (100 files)	1044.6 seconds

^∗Best energy reduction percentage.

As depicted in Table 2 using any mutation rate with number of generations of 1000, the energy reduction percentage is greater than 30%. The best energy reduction is achieved when the mutation rate is at 0.001 which is very promising being more than 50%. The computational time for all the 100 files is less than seven minutes. Therefore, it is around 4 seconds per file which is very much promising. To identify whether the differences between the averages with the changes in the mutation rates were significant, statistical analyses were carried out using the Freedman test.

Hypotheses

Null Hypothesis H₀. Means of minimized energy percentage for different mutation rates are the same
Alternative Hypothesis H₁. Means of minimized energy percentage for different mutation rates are not the same.

The p value = 0.000 <0.05 and we reject the null hypothesis and post hoc analysis has been carried out on the detailed dataset (Table 3) to determine which mutation rate has the highest mean percentage of reduction in energy.

Table 3. Detailed results of the GA.

CVRPLib file name	Rate of mutation
CVRPLib file name	0.0010	0.0025	0.0050	0.0075	0.0100
X-n1001-k43.vrp	12.80103	11.88827	10.85936	9.694029	9.556848
X-n101-k25.vrp	32.02678	35.75923	37.56841	40.00939	35.55532
X-n106-k14.vrp	30.27717	33.81137	34.26686	35.76881	33.72598
X-n110-k13.vrp	33.95242	40.20993	42.49106	39.00524	36.37393
X-n115-k10.vrp	50.81193	52.37917	55.09787	54.92929	53.33978
X-n120-k6.vrp	42.11564	45.09899	43.3998	44.35186	42.59954
X-n125-k30.vrp	26.52183	29.63255	31.01679	27.39243	27.4007
X-n129-k18.vrp	31.66396	33.715	34.8625	32.79096	32.22348
X-n134-k13.vrp	37.75922	42.5249	42.52067	42.57679	40.28671
X-n139-k10.vrp	37.36237	38.82001	38.74307	36.62869	35.8474
X-n143-k7.vrp	37.54207	43.38776	41.28395	37.84237	37.53593
X-n148-k46.vrp	31.93441	33.53385	34.04095	32.45357	30.09326
X-n153-k22.vrp	49.45064	49.81333	54.32997	52.78865	45.06589
X-n157-k13.vrp	42.86481	46.98111	45.72171	42.56459	42.47363
X-n162-k11.vrp	34.27922	38.17874	38.77056	37.83853	35.89787
X-n167-k10.vrp	31.62204	35.85662	37.1133	33.45995	32.22809
X-n172-k51.vrp	28.99557	34.80488	36.56064	29.37898	27.77682
X-n176-k26.vrp	39.44419	41.23805	40.69566	39.15282	36.88177
X-n181-k23.vrp	30.22022	33.84771	32.57614	30.78921	27.88417
X-n186-k15.vrp	34.75806	35.94411	33.87898	29.67616	30.61732
X-n190-k8.vrp	34.53248	36.59408	36.81079	36.82402	32.81114
X-n195-k51.vrp	31.78228	32.85653	29.30497	26.42445	22.69677
X-n200-k36.vrp	27.0885	28.60889	25.96263	24.49728	23.69031
X-n204-k19.vrp	31.70243	33.92431	30.44077	31.17991	27.19798
X-n209-k16.vrp	31.60467	32.05206	29.85411	27.84361	24.32678
X-n214-k11.vrp	32.55193	35.04465	33.91079	29.86931	64.77444
X-n219-k73.vrp	20.10571	22.6770	20.8841	19.1462	17.90529
X-n223-k34.vrp	30.40860	30.14028	29.89211	25.98539	20.03798
X-n228-k23.vrp	45.04471	45.64562	45.38162	40.09223	35.30641
X-n233-k16.vrp	31.90803	33.2655	33.22402	25.19938	25.45072
X-n237-k14.vrp	32.55161	32.68141	31.20284	30.6823	28.61488
X-n242-k48.vrp	23.91807	26.61617	20.90652	19.31902	14.68955
X-n247-k47.vrp	35.5378	38.53135	36.33797	30.11682	29.20752
X-n251-k28.vrp	30.01463	28.47438	24.65875	24.20706	22.11476
X-n256-k16.vrp	33.25466	34.19156	34.25381	28.92623	25.92442
X-n261-k13.vrp	29.70967	30.71204	28.49667	24.99286	23.82931
X-n266-k58.vrp	23.88774	26.97132	22.6137	17.39035	16.23727
X-n270-k35.vrp	27.88478	28.69578	24.80018	22.34739	20.61391
X-n275-k28.vrp	31.94181	32.22524	31.55025	29.16687	26.01753
X-n280-k17.vrp	36.40002	40.28805	37.492	31.2107	32.18607
X-n284-k15.vrp	29.24362	29.22297	25.84051	24.31867	22.31105
X-n289-k60.vrp	26.03244	24.4524	21.37549	17.71002	16.30786
X-n294-k50.vrp	27.29334	26.12614	22.5941	18.20006	16.88417
X-n298-k31.vrp	27.38218	25.41562	22.39082	18.86125	19.93721
X-n303-k21.vrp	27.91977	31.20337	25.23259	24.35885	20.68154
X-n308-k13.vrp	33.39066	36.73234	35.50009	32.08833	31.20307
X-n313-k71.vrp	24.28404	23.18796	19.81391	18.23606	16.86009
X-n317-k53.vrp	32.08766	31.86606	28.42572	25.00814	25.18776
X-n322-k28.vrp	25.12437	27.05396	23.15435	21.11874	17.37640
X-n327-k20.vrp	26.26653	26.12335	22.98445	21.70285	20.14563
X-n331-k15.vrp	29.44784	28.36366	27.57544	25.02837	22.02214
X-n336-k84.vrp	22.6318	22.90019	18.02802	16.15295	14.52159
X-n344-k43.vrp	24.32391	25.13196	22.02908	21.00029	17.65428
X-n351-k40.vrp	27.68809	26.01819	23.83853	22.73273	18.48367
X-n359-k29.vrp	21.84092	21.23801	17.35729	15.69808	13.77700
X-n367-k17.vrp	38.19213	33.30166	31.86441	27.12176	24.79421
X-n376-k94.vrp	20.09361	20.08725	17.43900	14.55602	15.48883
X-n384-k52.vrp	23.58085	23.29087	18.4361	17.41201	14.50117
X-n393-k38.vrp	25.30698	22.72104	19.75677	17.32702	16.88916
X-n401-k29.vrp	23.39231	21.57439	18.24951	18.13344	16.87411
X-n411-k19.vrp	39.58560	37.58242	31.96097	28.89972	25.96533
X-n420-k130.vrp	22.02357	21.37115	17.82149	15.26686	13.76679
X-n429-k61.vrp	22.76805	19.75252	15.07036	12.97871	14.51224
X-n439-k37.vrp	23.90484	25.4478	22.03636	19.64785	19.02882
X-n449-k29.vrp	22.58562	18.94513	16.51374	14.83471	13.86315
X-n459-k26.vrp	25.01886	25.35202	21.53826	19.56277	19.13728
X-n469-k138.vrp	15.98851	14.69173	13.00686	10.68891	10.80067
X-n480-k70.vrp	20.17462	18.28826	13.21342	13.50108	12.19322
X-n491-k59.vrp	22.35715	17.40456	16.12807	13.92029	12.32098
X-n502-k39.vrp	29.43752	28.93300	25.58213	23.71366	22.40697
X-n513-k21.vrp	20.66056	22.19829	17.66711	17.38231	15.59318
X-n524-k137.vrp	29.25552	25.00689	21.94620	18.42015	16.28576
X-n536-k96.vrp	22.00046	21.26785	15.21787	14.84602	13.92225
X-n548-k50.vrp	20.21664	19.10249	16.73358	17.28269	15.87240
X-n561-k42.vrp	19.32241	17.75355	14.06087	12.41879	12.15678
X-n573-k30.vrp	24.01248	23.39799	19.72642	18.85806	16.65078
X-n586-k159.vrp	17.84853	14.28692	13.70556	10.91328	10.95873
X-n599-k92.vrp	17.81388	15.09005	12.12366	11.29734	10.65991
X-n613-k62.vrp	19.58326	15.61245	13.32296	11.98591	11.20262
X-n627-k43.vrp	21.24216	18.5817	15.72306	13.56177	15.04474
X-n641-k35.vrp	17.08436	16.39485	13.36082	13.64283	11.30660
X-n655-k131.vrp	15.48288	14.88927	12.54741	12.25737	11.85345
X-n670-k126.vrp	28.71788	26.85190	20.31016	19.55446	17.42389
X-n685-k75.vrp	18.45748	15.06038	12.07450	10.94300	11.51439
X-n701-k44.vrp	16.57985	12.76328	11.40417	9.379679	8.427837
X-n716-k35.vrp	20.86056	19.27732	16.90755	14.85372	15.44707
X-n733-k159.vrp	17.96192	15.17854	12.20108	10.38958	8.888177
X-n749-k98.vrp	15.74652	14.80900	10.89733	11.00262	9.564129
X-n766-k71.vrp	27.54911	24.8529	19.96212	16.19431	13.99631
X-n783-k48.vrp	16.50255	11.88705	10.22504	12.07379	10.41174
X-n801-k40.vrp	17.87667	16.77141	14.99016	13.30332	13.53483
X-n819-k171.vrp	14.42093	13.74995	11.63282	11.58539	11.08715
X-n837-k142.vrp	13.10938	10.77977	9.634830	7.912295	9.019517
X-n856-k95.vrp	16.6359	15.19706	13.46041	13.24301	12.79089
X-n876-k59.vrp	16.99766	12.49846	13.28471	10.75942	11.86574
X-n895-k37.vrp	15.00296	14.3762	13.11793	11.61722	10.35098
X-n916-k207.vrp	11.61902	10.47219	8.532556	7.726192	7.366569
X-n936-k151.vrp	25.03095	24.13244	17.19300	14.26762	14.49740
X-n957-k87.vrp	14.77510	14.11095	12.44374	12.33696	11.75502
X-n979-k58.vrp	14.69893	12.25920	11.47749	9.918681	9.964106

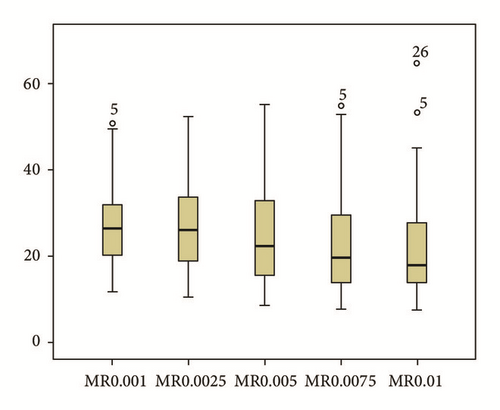
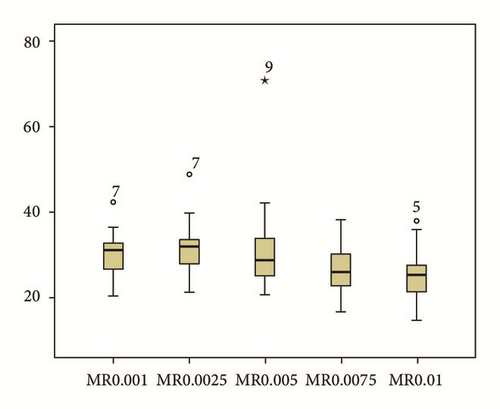
According to the box and whisker plot, mutation rate of 0.0025 is showing the highest mean value; hence, it can be concluded with 95% confidence interval that 0.0025 will generate better energy reductions for EMVRP when using population size of 50 and generations size of 100 (Figure 3).

5.2. Analysis of Performance of Parameter Tuned GA

As mentioned in the previous section, before applying the developed genetic algorithm, data on the CVRPLib has been clustered using k-means clustering algorithm into three clusters (Cluster 0, Cluster 1, and Cluster 2). The idea of clustering is to check the impact of characteristics of data on parameter tuning of the GA. The parameter considered for tuning is the rate of mutation. As for the experimental study, the 100 files used in the earlier experiment have been used. The clusters are created using number of cities to be served and total accumulated demand of a particular tour. To analyze the performance of GA on different clusters of data, the design of experiment has been utilized (Table 4).

Table 4. Design of experiment of tuned GA with CVRPLib data clusters.

Selected parameter	Values
Number of data files	100
Mutation rates	0.0010, 0.0025, 0.0050, 0.0075, 0.0100
Replications	5 per one mutation rate
Size of the population	50
Size of the generations	100

The rationale behind the experiment in Table 4 is to assess whether there is a significant difference among the reductions of energy percentages when the mutation rate is changed.

5.3. Results of CVRPLib Data Cluster 0

Null Hypothesis H₀. Means of minimized energy percentage for different mutation rates are the same.
Alternative Hypothesis H₁. Means of minimized energy percentage for different mutation rates are not the same.

The p value = 0.000 <0.05 and we reject the null hypothesis and post hoc analysis has been carried out on the detailed dataset (Table 5) to determine which mutation rate yields the highest percentage in reduction of energy.

Table 5. Average percentage of reduction of energy for Data Cluster 0.

CVRPLib file name	Rate of mutation
CVRPLib file name	0.0001	0.0025	0.005	0.0075	0.01
(X-n101-k25,5147.0,101.0)	30.2795	36.2461	37.7101	37.9236	35.2168
(X-n106-k14,13011.0,106.0)	32.0238	32.833	36.2804	35.2223	30.4027
(X-n110-k13,13827.0,110.0)	33.0007	37.1898	41.2574	38.6756	40.5764
(X-n115-k10,15362.0,115.0)	49.5449	50.5952	55.6424	54.8956	51.0182
(X-n120-k6,15481.0,120.0)	41.4965	43.7106	45.6016	45.7964	41.0161
(X-n125-k30,21017.0,125.0)	24.5716	28.4982	30.0036	28.8937	26.8316
(X-n129-k18,21682.0,129.0)	31.0658	33.7182	34.406	33.0458	32.7406
(X-n134-k13,29902.0,134.0)	40.4161	44.4603	43.73	43.9817	41.7856
(X-n139-k10,30941.0,139.0)	37.7481	38.4019	41.7096	38.2775	35.7362
(X-n143-k7,38416.0,143.0)	36.1435	42.5054	39.74	39.2316	36.9879
(X-n148-k46,39233.0,148.0)	28.6224	35.0103	33.176	32.0835	26.2372
(X-n153-k22,42301.0,153.0)	47.0119	49.6091	50.3011	50.222	46.9372
(X-n157-k13,42457.0,157.0)	44.5515	46.5625	46.7771	43.414	42.4649
(X-n162-k11,54651.0,162.0)	33.8149	38.9795	42.114	36.896	34.6667
(X-n167-k10,55887.0,167.0)	34.3191	39.1482	34.7953	33.867	30.1161
(X-n172-k51,63979.0,172.0)	30.9868	34.2055	31.901	29.9517	25.5072
(X-n176-k26,67611.0,176.0)	37.8435	43.655	40.7705	40.2538	38.4579
(X-n181-k23,67791.0,181.0)	32.5043	32.0691	34.2579	31.2722	29.6108
(X-n186-k15,81644.0,186.0)	32.5559	34.7171	34.9303	32.4279	28.6864
(X-n190-k8,82687.0,190.0)	35.493	35.8647	38.8699	35.8953	32.1755
(X-n195-k51,91895.0,195.0)	30.3231	32.635	32.6071	27.5018	25.8458

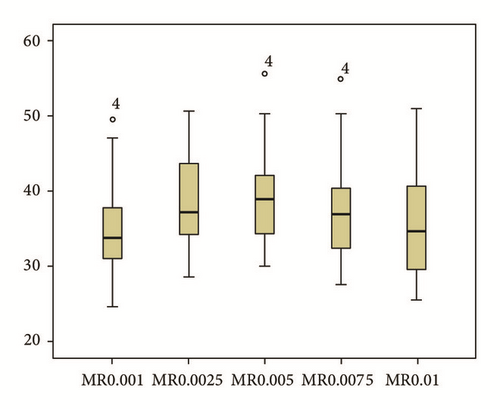
According to the box and whisker plot, mutation rate of 0.05 is showing the highest mean in the percentage reduction in energy. Hence, it can be concluded with 95% confidence interval that 0.05 generates better energy reductions for Cluster 0 (Figure 4).

5.4. Results of CVRPLib Data Cluster 1

Null Hypothesis H₀. Means of minimized energy percentage for different mutation rates are the same.
Alternative Hypothesis H₁. Means of minimized energy percentage for different mutation rates are not the same.

The p value = 0.000 <0.05 and we reject the null hypothesis and post hoc analysis has been carried out on the detailed dataset (Table 6) to determine which mutation rate has the highest mean.

Table 6. Average percentage of reduction of energy for Data Cluster 1.

CVRPLib file name	Rate of mutation
CVRPLib file name	0.0001	0.0025	0.005	0.0075	0.01
(X-n200-k36,106158.0,200.0)	25.8922	28.244	25.4307	24.8176	21.5926
(X-n204-k19,121293.0,204.0)	31.7862	33.3268	31.0833	27.8423	28.1407
(X-n209-k16,122840.0,209.0)	29.6146	33.0459	27.9114	27.624	25.0044
(X-n214-k11,133196.0,214.0)	32.4836	32.4988	34.1668	28.6341	27.2371
(X-n219-k73,133414.0,219.0)	20.4221	21.3139	20.8364	18.7089	37.9443
(X-n223-k34,134648.0,223.0)	30.2742	33.6129	30.2504	23.4108	24.9498
(X-n228-k23,138126.0,228.0)	42.3674	48.8541	42.1286	38.2606	35.9466
(X-n233-k16,148219.0,233.0)	31.7538	35.2122	30.4283	26.9163	27.2217
(X-n237-k14,148455.0,237.0)	34.5302	33.6068	70.7867	32.2174	29.0436
(X-n242-k48,149779.0,242.0)	25.3818	26.5639	22.9681	18.7777	17.4704
(X-n247-k47,155979.0,247.0)	36.489	39.7815	35.6563	30.8481	28.9909
(X-n251-k28,157846.0,251.0)	27.3622	31.0231	26.4525	22.6824	20.6356
(X-n256-k16,177360.0,256.0)	32.9859	33.1934	33.5661	31.6681	25.8602
(X-n261-k13,190741.0,261.0)	31.9163	29.6783	28.0676	24.9275	21.9564
(X-n266-k58,192756.0,266.0)	24.7841	23.4658	21.208	17.4536	17.1201
(X-n270-k35,213175.0,270.0)	27.9878	28.8698	26.5334	22.7852	21.0692
(X-n275-k28,213449.0,275.0)	32.2499	31.4036	29.4528	29.5828	26.7106
(X-n280-k17,216682.0,280.0)	34.7643	38.5678	36.3531	34.8625	25.8963
(X-n284-k15,218209.0,284.0)	30.5936	27.6397	25.0705	25.1467	22.4253
(X-n289-k60,234183.0,289.0)	23.5243	24.7778	21.3323	16.7366	14.785

According to the box and whisker plot, mutation rate of 0.0025 is showing the highest median value; hence, it can be concluded with 95% confidence interval that 0.0025 will generate better energy reductions for Cluster 1 (Figure 5).

5.5. Results of CVRPLib Data Cluster 2

Null Hypothesis H₀. Means of minimized energy percentage for different mutation rates are the same.
Alternative Hypothesis H₁. Means of minimized energy percentage for different mutation rates are not the same.

The p value = 0.000 <0.05 and we reject the null hypothesis and post hoc analysis has been carried out on the detailed dataset (Table 7) to determine which mutation rate has the highest mean.

Table 7. Average percentage of reduction of energy for Data Cluster 2.

CVRPLib file name	Rate of mutation
CVRPLib file name	0.0001	0.0025	0.005	0.0075	0.01
X-n1001-k43.vrp	12.827504	11.715805	9.88541	10.448598	8.5876013
X-n294-k50.vrp	25.533544	25.854934	19.708729	18.366514	16.064914
X-n298-k31.vrp	25.725572	25.218533	22.642264	18.163332	16.76971
X-n303-k21.vrp	27.279439	32.206786	26.958772	22.055703	22.331427
X-n308-k13.vrp	37.079786	37.304107	35.981044	30.050856	30.860439
X-n313-k71.vrp	24.308694	23.646315	19.792177	16.502028	15.505046
X-n317-k53.vrp	30.92691	31.23127	28.24586	25.473993	25.535702
X-n322-k28.vrp	25.964802	25.395741	22.888762	21.486427	19.010605
X-n327-k20.vrp	25.915225	28.059972	23.76868	21.030628	20.912205
X-n331-k15.vrp	27.524263	27.977593	25.065238	24.569392	22.226545
X-n336-k84.vrp	24.156591	20.834126	17.204415	13.497206	14.088004
X-n344-k43.vrp	26.146141	23.651449	20.511471	15.331793	15.746694
X-n351-k40.vrp	26.616442	27.407423	23.158878	18.557153	18.888495
X-n359-k29.vrp	24.174821	23.677236	16.568104	16.769655	16.189016
X-n367-k17.vrp	37.507069	36.93659	33.44967	28.866205	28.357283
X-n376-k94.vrp	19.829914	18.384511	16.634847	15.279178	14.862174
X-n384-k52.vrp	22.773069	21.093078	18.998565	15.645967	14.923587
X-n393-k38.vrp	24.073648	23.581917	18.655457	18.284506	13.701024
X-n401-k29.vrp	22.379471	22.160249	18.760097	16.242995	15.404726
X-n411-k19.vrp	40.168322	37.421562	31.271868	27.884874	30.411745
X-n420-k130.vrp	21.897389	21.619467	16.981261	17.189068	13.689977
X-n429-k61.vrp	20.845623	17.722107	18.414669	15.042775	13.250864
X-n439-k37.vrp	25.2498	24.724619	23.048158	20.482543	19.241802
X-n449-k29.vrp	22.699744	18.136894	16.015191	14.389112	14.01591
X-n459-k26.vrp	25.5812	25.288133	21.133864	19.248823	18.753649
X-n469-k138.vrp	16.436619	14.524521	11.857235	11.05651	10.132928
X-n480-k70.vrp	18.390041	17.002514	14.246622	14.659912	12.984294
X-n491-k59.vrp	23.596872	19.402038	15.007576	13.256561	14.380208
X-n502-k39.vrp	28.250292	28.665693	25.821766	23.507696	22.389436
X-n513-k21.vrp	22.116418	19.963564	18.940326	16.178493	14.949564
X-n524-k137.vrp	28.219495	26.851244	20.376538	17.192628	16.736019
X-n536-k96.vrp	23.001011	20.568751	16.76173	16.488653	14.923288
X-n548-k50.vrp	20.281627	19.318569	16.651976	14.723431	14.636057
X-n561-k42.vrp	19.084868	17.423921	14.60639	15.02745	12.550507
X-n573-k30.vrp	24.638549	21.655251	19.526443	17.813234	16.501781
X-n586-k159.vrp	17.464901	15.448383	12.99529	13.177791	12.257662
X-n599-k92.vrp	17.846692	15.155531	13.045469	12.320552	10.514622
X-n613-k62.vrp	17.128463	16.110833	13.362154	12.063181	11.614861
X-n627-k43.vrp	21.567104	17.753015	14.741696	14.799587	13.825805
X-n641-k35.vrp	17.920677	17.321866	14.078229	12.711317	12.318776
X-n655-k131.vrp	15.962562	13.796249	12.337187	11.534519	10.876943
X-n670-k126.vrp	27.925595	25.990998	19.859656	16.643033	14.84004
X-n685-k75.vrp	19.123097	15.352256	13.352629	11.422474	12.132536
X-n701-k44.vrp	14.817606	13.860182	10.16125	11.001818	9.2017285
X-n716-k35.vrp	22.93946	18.60758	16.68929	14.603138	16.022459
X-n733-k159.vrp	17.752462	14.108984	10.329737	12.149165	9.6394828
X-n749-k98.vrp	16.501435	12.987899	11.393273	10.471188	9.3638983
X-n766-k71.vrp	25.594234	25.868375	21.526236	18.644464	14.898724
X-n783-k48.vrp	16.315407	12.343775	11.520721	9.696421	10.501402
X-n801-k40.vrp	16.916469	15.886679	13.943067	13.577301	12.386437
X-n819-k171.vrp	14.896745	14.002887	12.156429	11.572758	10.604485
X-n837-k142.vrp	12.668758	10.664722	8.3282448	9.0021583	7.7984541
X-n856-k95.vrp	15.931693	16.107941	14.412979	12.662221	12.718295
X-n876-k59.vrp	17.512326	14.775116	10.77695	11.211426	11.920959
X-n895-k37.vrp	14.636802	12.045023	11.659649	12.339187	11.006958
X-n916-k207.vrp	11.556926	10.198883	8.571053	8.233212	7.1698279
X-n936-k151.vrp	27.588469	24.401292	17.427975	14.002693	14.131898
X-n957-k87.vrp	15.921267	14.435585	13.276304	12.420921	10.195919
X-n979-k58.vrp	15.763138	12.940315	10.150284	10.668937	9.7730485

According to the box and whisker plot, mutation rate of 0.001 is showing the highest mean value; hence, it can be concluded with 95% confidence interval that 0.001 will generate better energy reductions for Cluster 1 (Figure 6).

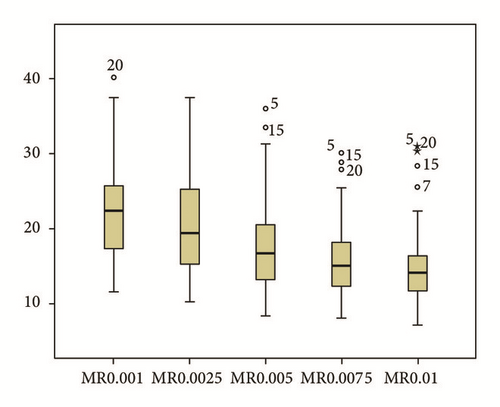
From the results obtained for these three clusters, it has been significantly shown that mutation rates will work best for particular clusters shown in Table 8.

Table 8. Best mutation rates for data clusters.

Data cluster identified	Best mutation rate
Cluster 0	0.0500
Cluster 1	0.0025
Cluster 2	0.0010

These results depict the importance of identifying and using different parameter settings when designing GAs to solve EMVRP instances which have different characteristics. As it has been noted in first set of results obtained just using the GA, the best mutation rate has been 0.001 for any problem instance. However, when CVRPLib data was clustered into three distinctive clusters and extensive parameter tuning was carried out, the best mutation rates were different. Thus, it can be concluded that machine learning techniques such as clustering have improved the solution quality immensely compared with a generic untuned GA.

6. Conclusions

This study adds new knowledge to the VRP literature in several ways. Initially, the systematic review which was carried out on the problem solving methods of Green VRP can be seen as the first study to focus on that segment. Then, developing two classes of GAs to solve the EMVRP using the CVRPLib data repository can be seen as another. The EMVRP is the problem which looks at finding routes of vehicles which use the least amount of energy when serving a set of cities or customers. In EMVRP, the energy is generalized to be equal to a function of load and distance. As the first instance of using metaheuristics for EMVRP, untuned and tuned genetic algorithms have been developed and detailed analyses have been carried out through rigorous data analyses. The developed algorithms have been proven to generate competitive solutions within reasonable computational times as depicted in the analyses. Further, this study looked at the GA parameter tuning as a prominent design aspect in coming up with flexible and adaptive GAs which are highly dependent upon the inherent characteristics of problem instances. The authors have utilized different mutation rates to improve the performance of the GAs using a very novel approach of applying k-means clustering, the machine learning technique. It has been proved that identifying different clusters within data has a significant impact on improving the performance of GA.

The following highlights the contributions made through this study:

(1)
A systematic review of the literature on the Green VRP solving methods
(2)
First instance of solving EMVRP using genetic algorithms
(3)
First instance of the applicability of machine learning techniques for parameter tuning of metaheuristics

This study can be further worked on by relaxing the assumptions considered in EMVRP formulation with the use of heterogeneous vehicles, considering the actual weight of the vehicle and continuous loads. Furthermore, by developing a path-based metaheuristic such as Tabu search to solve EMVRP and comparing its performance against the population-based GAs, this study can be easily extended by developing a more realistic cost function to reduce the energy. Finally, researching the applicability of other machine learning-based mechanisms to augment metaheuristics would be another interesting and important research area for future research.

Competing Interests

The authors declare that there are no competing interests regarding the publication of this paper.

References

1 Kara I., Kara B. Y., and Kadri Yetis M., Energy minimizing vehicle routing problem, Combinatorial Optimization and Applications, 2007, 4616, Springer, Berlin, Germany, 62–71, Lecture Notes in Computer Science, https://doi.org/10.1007/978-3-540-73556-4_9, MR2391850.
10.1007/978-3-540-73556-4_9
Google Scholar
2 Gendreau M., Metaheuristics in vehicle routing, Proceedings of the International Conference on Operations Research and Enterprise Systems (ICORES ′12), 2012.
Google Scholar
3 Birattari M., Tuning Metaheuristics: A Machine Learning Perspective, 2009, 197, Springer, Berlin, Germany.
10.1007/978-3-642-00483-4
Web of Science® Google Scholar
4 Gendreau M., Potvin J. Y., Bräumlaysy O., Hasle G., and Løkketangen A., Metaheuristics for the vehicle routing problem and its extensions: a categorized bibliography, The Vehicle Routing Problem: Latest Advances and New Challenges, 2008, Springer US, 143–169.
10.1007/978-0-387-77778-8_7
Google Scholar
5 Lin C., Choy K. L., Ho G. T. S., Chung S. H., and Lam H. Y., Survey of green vehicle routing problem: past and future trends, Expert Systems with Applications. (2014) 41, no. 4, 1118–1138, https://doi.org/10.1016/j.eswa.2013.07.107, 2-s2.0-84888351443.
10.1016/j.eswa.2013.07.107
Web of Science® Google Scholar
6 Yazan D. M., Petruzzelli A. M., and Albino V., Analyzing the environmental impact of transportation in reengineered supply chains: a case study of a leather upholstery company, Transportation Research Part D: Transport and Environment. (2011) 16, no. 4, 335–340, https://doi.org/10.1016/j.trd.2011.01.003, 2-s2.0-79952315776.
10.1016/j.trd.2011.01.003
Web of Science® Google Scholar
7 Björklund M., Influence from the business environment on environmental purchasing—drivers and hinders of purchasing green transportation services, Journal of Purchasing and Supply Management. (2011) 17, no. 1, 11–22, https://doi.org/10.1016/j.pursup.2010.04.002, 2-s2.0-78651283671.
10.1016/j.pursup.2010.04.002
Web of Science® Google Scholar
8 Leipzig I. T. F., Reducing Transport Greenhouse Gas Emissions: Trends & Data, 2010, Background for the 2010 International Transport Forum, Berlin, Germany.
Google Scholar
9 Lenstra J. K. and Kan A. H. G. R., Complexity of vehicle routing and scheduling problems, Networks. (1981) 11, no. 2, 221–227, https://doi.org/10.1002/net.3230110211, 2-s2.0-0019572333.
10.1002/net.3230110211
Web of Science® Google Scholar
10 Holland J. H., Adaptation in Natural and Artificial Systems: An Introductoryanalysis with Applications to Biology, Control, and Artificial Intelligence, 1975, University of Michigan Press, Ann Arbor, Mich, USA, MR0441393.
Google Scholar
11 Dobslaw F., A parameter tuning framework for metaheuristics based on design of experiments and artificial neural networks, Proceedings of the International Conference on Computer Mathematics and Natural Computing (WASET ′10), 2010.
Google Scholar
12 Cooray P. L. N. U. and Rupasinghe T. D., An analysis of methodologies for solving green vehicle routing problem: a systematic review of literature, Proceedings of the Conference on Research for Transport and Logistics Industry, 2016, Colombo, Sri Lanka.
Google Scholar
13 Uchoa E., Pecin D., Pessoa A., Poggi M., Subramanian A., and Vidal T., New benchmark instances for the capacitated vehicle routing problem, Research Report Engenharia de Produção, 2014, Universidade Federal Fluminense.
Google Scholar

Citing Literature

All articles

Machine Learning-Based Parameter Tuned Genetic Algorithm for Energy Minimizing Vehicle Routing Problem

Abstract

1. Introduction