With the ever increasing global energy demand and diminishing petroleum reserves, current advances in drilling technology have resulted in numerous directional wells being drilled as operators strive to offset the ever-rising operating costs. In as much as deviated-well drilling allows drillers to exploit reservoir potential by penetrating the pay zone in a horizontal, rather than vertical, fashion, it also presents conditions under which the weighting agents can settle out of suspension. The present work is categorized into two parts. In the first part, governing equations were built inside a two-dimensional horizontal pipe geometry and the finite element method utilized to solve the equation-sets. In the second part, governing equations were built inside a three-dimensional horizontal annular geometry and the finite volume method utilized to solve the equation-sets. The results of the first part of the simulation are the solid concentration, mixture viscosity, and a prediction of the barite bed characteristics. For the second part, simulation results show that the highest occurrence of barite sag is at low annular velocities, nonrotating drill pipe, and eccentric drill pipe. The CFD approach in this study can be utilized as a research study tool in understanding and managing the barite sag problem.

1. Introduction

With the ever increasing global energy demand and diminishing petroleum reserves, recent advances in drilling technology have resulted in numerous directional wells being drilled as operators strive to offset the ever-rising operating costs. Deviated-well drilling allows operators to exploit reservoir potential by penetrating the pay zone in a horizontal, rather than vertical, fashion. With consideration of eliminating drilling problems such as stuck pipe, torque and drag, wellbore instability, and low rates-of-penetration, these wells are being drilled increasingly with invert-emulsion drilling fluids.

In the drilling industry, the term “barite sag” refers to the settling of weighting materials in drilling fluids under flowing (pumping) or no flowing (no pumping) conditions. In as much as there exist substitutes such as iron titanium oxide, calcium carbonate, and manganese tetra oxide, barite is used extensively since it provides high density with wide accessibility and favourable economics and it is ecofriendly. Notwithstanding mentioning, the API 13D defines barite sag (in the field) as the change in drilling fluid density observed when circulating bottoms-up; it is almost always characterized by drilling fluid having a density below nominal, being followed by drilling fluid densities above nominal, and being circulated out of the annulus [1].

Modelling and simulation studies employ a combination of both mathematical formulations and numerical techniques where the governing equations for a problem definition are solved by either writing a computer program (code) following a discretization scheme such as finite difference method (FDM) or using CFD software to obtain a solution following a numerical method such as finite element method (FEM) or finite volume method (FVM). The solution obtained is referred to as a numerical solution since a particular numerical procedure is followed and the whole process generally called numerical simulation. Numerous researchers have studied the barite sag phenomenon by employing modelling and simulation studies.

Paslay et al. [2] presented a fundamental theoretical effort to describe dynamic sag in drilling fluids by considering the behaviour of a system of particles in a non-Newtonian Bingham fluid. The authors employed continuum mechanics to develop a model of dynamic sag in an inclined annulus in terms of the fluid and particle properties. They focused on the period when pumping and rotation are stopped. They indicated that the particles settle for a few minutes immediately following the cessation of rotation and pumping when the gelling properties of the stationary drilling fluid have not been fully recovered. The analysis upon which the results were deduced is laminar flow and the predictions appeared to be consistent with the operational guidelines presented by Dye et al. [3].

Nguyen et al. [4] described a fundamental mathematical approach (based mainly on the continuum methodology) to examine the sedimentation of barite particles in shear flow of Newtonian fluids; they established a numerical method to solve four partial differential equation-sets describing dynamic barite sag in pipe flow of Newtonian fluids. They calculated the concentration of solid in both the axial and radial directions as a function of time by using an explicit FDM method.

Hashemian et al. [6, 7] performed a study on barite sag by (1) modelling of laminar flow of non-Newtonian fluid in annulus to obtain velocity profile and (2) consideration of the solid particles in the fluid to predict the particle traveling path and time. The simulation was based on a proposed particle tracking method called “Particle Elimination Technique.” It is important to note that the simulation approach employed is much dependent on a parallel experimental study. The estimation of unknown parameters (, mass rate of barite bed back to suspension, , average velocity of the barite bed, and µ, viscosity of the barite bed) that are input parameters in the simulation is based on the experimental results. This is rather a shortcoming of this approach as it cannot be performed independently and later make a comparison with experimental data.

Kulkarni et al. [8] presented a novel method of predicting real-time sag behaviour in the wellbore by employing a comprehensive computational approach to model the sag behaviour in wellbores using fluids composition (i.e., weight-material (barite) size/concentration and oil-water ratio)/properties (i.e., rheology) and wellbore geometry (i.e., inclination and diameter)/operating conditions (i.e., temperature, pressure, and time for which the fluid is uncirculated) information. The model developed was referred to as the wellbore sag model (WSM). The authors reported that, generally, the WSM captured the appropriate characteristics of the fluids and successfully predicted their respective sag behaviour.

The objective of this paper is to present an entirely independent numerical simulation study on barite sag in pipe and annular sections by employing CFD. Additionally, a CFD-DEM approach, based on preliminary results, is proposed for future research on the study of barite sag in annular sections.

2. Mathematical Approach

The mathematical approach is in two parts. In the first part, the governing equations are built inside a two-dimensional horizontal pipe geometry and the finite element method (FEM) utilized to solve the equation-sets, for studying the solid concentration distribution of a solid-liquid system in pipe flow. In the second part, governing equations are built inside a three-dimensional horizontal annular geometry and the finite volume method (FVM) utilized to solve the equation-sets, for studying the barite sag phenomenon in an annulus under flow conditions.

2.1. Horizontal Pipe Section

Description of the Eulerian-Eulerian approach to study the solid concentration distribution in a pipe in shear flow of a solid-liquid system: This model assumes that solid concentration only changes in the axial and lateral directions. In addition, the model is developed under laminar flow conditions.

2.1.1. Mass Balance

Assuming that the mass transfer between the two phases is zero, the following continuity relations hold for the continuous and dispersed phase [9]:

(1)

Here ϕ (dimensionless) denotes the phase volume fraction, ρ (kg/m³) is the density, and u (m/s) is the velocity of each phase. The subscripts c and d denote quantities relating to the continuous and dispersed phase, respectively. The following relation between the volume fractions must hold

(2)

Both phases are considered incompressible, in which case (1) can be simplified as

(3)

(4)

When (3) and (4) are added together, a continuity equation for the mixture is obtained:

(5)

In order to control the mass balance of the two phases, the Euler-Euler model interface solves (4) together with (5). Equation (4) is used to compute the volume fraction of the dispersed phase, and (5) is used to compute the mixture pressure.

2.1.2. Momentum Balance

The momentum equations for the continuous and dispersed phases, using the nonconservative forms of Ishii [10], are

(6)

(7)

Here P (Pa) is the mixture pressure, which is assumed to be equal for the two phases. The viscous stress tensor for each phase is denoted by τ (Pa), g (m/s²) is the vector of gravitational acceleration, F_m (N/m³) is the interphase momentum transfer term (that is, the volume force exerted on each phase by the other phase), and F (N/m³) is any other volume force term.

For fluid-solid mixtures, (7) is modified in the manner of Enwald et al. [11]

(8)

The fluid phases in the above equations are assumed to be Newtonian and the viscous stress tensors are defined as

(9a)

(9b)

where µ (Pa·s) is the dynamic viscosity of the respective phase.

In order to avoid singular solutions when the volume fractions tend to zero, the governing equations above are divided by the corresponding volume fraction. The implemented momentum equations for the continuous and dispersed phase are as given in (10) and (11), respectively.

(10)

(11)

2.1.3. Dispersed Phase Viscosity

Using an expression for the mixture viscosity, the default values for the dynamic viscosities of the two interpenetrating phases are taken as

(12)

A simpler mixture viscosity covering the entire range of particle concentrations is the Krieger type [12]:

(13)

where ϕ_d,max is the maximum packing limit, by default 0.62 for solid particles. Equation (13) can be applied when μ_c ≪ μ_d.

On the other hand, user-defined expressions for the dispersed phase and mixture viscosity can be employed [4]:

(14a)

(14b)

(14c)

where μ (SI unit: Pa·s) is viscosity and the subscripts c, d, and mix represent continuous phase, dispersed phase, and mixture, respectively; C is the dispersed phase concentration.

2.1.4. Interphase Momentum Transfer

The drag force added to the momentum equation is defined as

(15)

where F_drag,c is the drag force on the continuous phase, F_drag,d is the drag force on the dispersed phase, β is a drag force coefficient, and the slip velocity is defined as

(16)

2.1.5. Dilute Flows

For dilute flows the drag force coefficient β can be modelled as

(17)

In this case drag coefficient can be computed from the Schiller-Naumann model in (18), where the particle Reynolds number is given as in (19):

(18)

(19)

2.1.6. Solid Pressure

For fluid-solid mixtures, a model for the solid pressure, P_s, in (11), is needed. The solid pressure models the particle interaction due to collisions and friction between the particles. The solid pressure model implemented uses a gradient diffusion based assumption:

(20)

where the empirical function G (21) is given by (22) as described in Enwald et al. [11]

(21)

(22a)

(22b)

(22c)

2.2. Horizontal Annular Section

Description of the 3D model employed to study the behaviour of barite particles in an annulus based on the CFD approach is as follows.

2.2.1. Governing Equations for Fluid Flow

The local averaged Navier-Stokes equations describe the 3D equations of motion of viscous, unsteady, and incompressible fluid phase.

Mass Conservation Equations. The mass conservation equation is expressed as

(23)

where u_f is the fluid velocity, ρ_f is the fluid density, α_f is the volume fraction of the fluid phase, and t is the time.

Momentum Conservation Equations. The momentum conservation equation is expressed as

(24)

where p is the fluid pressure, τ_f is the viscous stress tensor, and S_f is the volume-averaged (on a cell) interaction forces (interphase momentum transfer source term between the particles and fluid). The stress tensor is defined as [13]

(25a)

(25b)

where μ_f is the solvent viscosity which is dependent on the shear rate,

is the shear rate, and D is the rate of deformation tensor (25a). In (25b), I is an identity matrix and the equation is valid for laminar flow. The shear rate is calculated from the second invariant of the rate of deformation tensor this is defined in (27).

(26)

(27)

And

, where u_f is the velocity field.

Rheology Model. The relationship between the shear stress and shear rate in the fluid phase is described by the non-Newtonian generalized power law model. The mathematical representation is shown in [13]

(28a)

(28b)

where a_T is the temperature shift factor (for an isothermal flow, a_T = 1), τ₀ is the yield stress threshold, μ₀ is the yielding viscosity, μ_min is the minimum viscosity limit, μ_max is the maximum viscosity limit, n is the power law exponent, and K is the consistency factor. The value of n determines the class of the fluid; that is, for n = 1, the fluid is Newtonian, n > 1, the fluid is shear-thickening (dilatant), and n < 1, the fluid is shear-thinning (pseudoplastic) or viscoelastic.

2.2.2. Governing Equations for Particle Flow

(I) Dispersed Phase Modelled as Lagrangian Phase

Basic Equations of Motion. The most basic particle description involves only its position r_p(t) and velocity v_p(t). These two quantities relate through the equation of motion [13]:

(29)

The grid velocity u_g(x, t) is evaluated at the particle position r_p(t); its appearance in (29) indicates that the convection is that u_p(t) is the absolute velocity of the particle, whereas r_p(t) is the position of the particle with respect to the frame of reference.

For parcels, individual particles are not tracked; instead a single parcel represents a set of identical particles, at some mean centroid r_π(t). The velocity of the parcel is assumed to be the same as its constituent particles; hence its equation of motion is

(30)

Mass Balance for a Material Particle. The equation of conservation of mass of a material particle is

(31)

where m_p is the mass of the particle and

the rate of mass transfer to the particle.

Mass Transfer. The rate of mass transfer to a single particle from the continuous phase is .

Momentum Balance for a Material Particle. The generic form of the equation of conservation of momentum of a material particle is

(32)

where F_S represents the forces acting on the surface of the particle, and F_B the body forces. These forces are in turn decomposed into

(33a)

(33b)

where F_D is the drag force, F_P is the pressure gradient force, F_g is the gravity force, and F_u is the user-defined body force.

(a) Drag Force. The equation for drag force is [14]

(34)

where C_d is the drag coefficient, ρ_f is the density of the fluid (continuous phase), A_P is the projected area of the particle, and u_s is the particle slip velocity (and is given as u_s = u_f − u_p).

(b) Drag Coefficient. The Schiller-Naumann correlation [14] is suitable for spherical solid particles (and liquid droplets and small-diameter bubbles). For a viscous continuous phase, the correlation is as defined in (18).

(c) Pressure Gradient Force. The equation for the pressure gradient force is [14]

(35)

where V_P is the volume of the particle, and ∇P_static is the gradient of the static pressure in the continuous phase.

(d) User-Defined Body Force. The equation for the user-defined body force is

(36)

where f_u is the user body force (per unit volume).

(e) Particle Shear Lift Force. This applies to a particle moving relative to a fluid where there is a velocity gradient in the fluid orthogonal to the relative motion. Saffman [12] gives the lift force as

(37)

where the y direction is the direction of the velocity gradient. The 3D version of (38) is

(38)

where ω_f is the curl of the fluid velocity (ω_f = ∇ × u_f) and C_LS is the shear lift coefficient. C_LS can be defined using either of two published definitions. Saffman [12] provides a definition that recovers the original Saffman asymptotic solution for low Reynolds numbers (39) and on the other hand, Sommerfeld [14] provides a definition for a broader range of Reynolds numbers (41).

(39)

(40)

(41)

in which β = 0.5Re_s/Re_P (0.005 < β < 0.4) and Reynolds number for shear flow is

Momentum Transfer. The rate of momentum transfer to a single particle from the continuous phase is , where F_S is as defined in (33a).

Boundary Interface Mode. It is important to formulate the Lagrangian phase boundary interaction mode [13].

Rebounding particles remain active in the simulation; the mode is distinguished by its treatment of the particle velocity. The rebound velocity relative to the wall velocity is determined by the impingement velocity and user-defined restitution coefficients:

(42)

The superscripts R and I denote rebound and impingement, respectively; the subscripts n and t denote wall-normal and tangential, respectively. Since the left hand side of (42) can be split into orthogonal n and t components, it can be split into two equations

(43a)

(43b)

which serve to emphasize the definition of the restitution coefficients as the constants of proportionality between impingement and rebound velocities. Both coefficients may range from 0 to 1; the latter is “perfect” elastic rebound. The tangential velocity of a wall boundary is zero unless a value is explicitly prescribed through a wall sliding option. In other words, it is nonzero only at no-slip walls.

(II) Dispersed Phase Modelled as DEM Particles. The detailed description is shown in the appendix.

3. Model Configuration

3.1. 2D Model: Horizontal Pipe Section

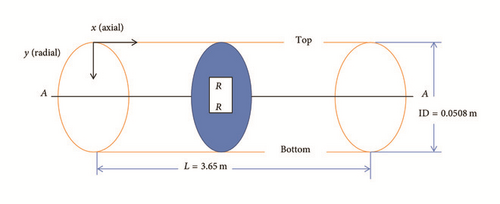
For the physical model of a horizontal pipe section with ID 0.0508 m (2 in.) and length 3.65 m (12 ft) see Figure 1. For the discretized representation of the computational domain which the physics solvers use to provide a numerical solution, the mesh is shown in Figure 2. Table 1 lists the inputs used in the 2D configuration. Additionally, the assumptions and boundary conditions are listed below.

Table 1. Input data for the simulation – 2D CFD model.

Parameter	Variable	Value	Units
Diameter of pipe	D_P	0.0508 (2)	m (in.)
Length of pipe	L	3.65 (12)	m (ft.)
Fluid inlet velocity	u_f	0.1556 (30.64)	m/s (ft/min)
Viscosity of liquid	μ_L	0.062 (62)	Pa·s (cP)
Density of liquid	ρ_L	898.78 (7.5)	kg/m³ (lb_m/gal)
Density of solid	ρ_s	4198.92 (35)	kg/m³ (lb_m/gal)
Diameter of solid	d_s	0.000025 (25)	m (µm)
Initial concentration of the solid	C_o	0.067
Deviation angle	θ	90	° (from vertical)
Number of CFD elements		63,790
CFD time-step	Δt_CFD	0.1	s
Physical time simulated	t_end	36	s

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Horizontal pipe section, L = 3.65 m (12 ft) and ID = 0.0508 m (2 in.).

Assumptions

(i)
Every single phase of the mixture behaves as if it was a lone phase, with the exception of the case when interacting with the other phase.
(ii)
The equations of motion describing the mixture are similarly those for a single phase and are the consequence of the summation motion equations for the individual phases over all phases.
(iii)
Flow of the liquid phase is in one direction (that is, axial), whereas that of the solid phase is in two directions (both axial and radial).
(iv)
The liquid and solid densities are constant; in other words, phases are incompressible.
(v)
There is no consideration of Brownian motion.
(vi)
There is no particle interaction arising from collisions and friction between the particles. Thus, solid pressure is neglected.
(vii)
Wall effects are neglected.
(viii)
Isothermal and laminar flow are considered.

Boundary Conditions

(i)
No-slip condition at the walls.
(ii)
Inlet boundary conditions, that is, velocity inlet.
(iii)
Outlet boundary conditions, that is, pressure outlet.

3.2. 3D Model: Horizontal Annular Section

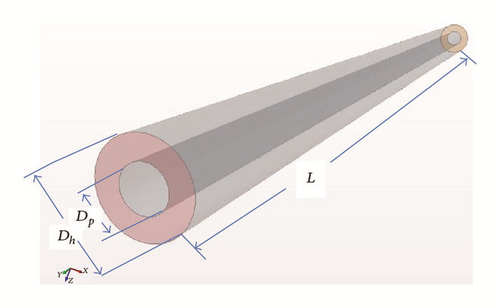
The physical model is an annular test section as depicted in Figure 3. Figure 3(a) shows the physical model for a concentric annular section whereas Figure 3(b) depicts an eccentric annular section. For the discretized representation of the computational domain which the physics solvers use to provide a numerical solution, the mesh is shown in Figure 4. Table 2 lists the inputs used in the 3D configuration. Additionally, the assumptions and boundary conditions are listed below.

Table 2. Input for the simulation – 3D CFD model; dispersed phase modelled as Lagrangian phase.

Parameter	Variable	Value	Units
Drill string length	L	1.8288 (6)	m (ft.)
Pipe diameter	D_p	0.0508 (2)	m (inch)
Hole diameter	D_h	0.1016 (4)	m (inch)
Angle of inclination	θ	0–90	° (degrees)
Fluid inlet velocity	u_f	0.1524 (30)–0.762 (150)	m/s (ft./min)
Dynamic viscosity	μ_f
Density of liquid	ρ_f	958.61 (8.0)	kg/m³ (ppg)
Fluid behaviour index	n	0.44	—
Consistency index	K	0.63 (1.316)	Pa·s ⁿ (lbfs ⁿ/100 ft²)
Drill pipe rotation speed	ω_drillpipe	0–100	rpm
Eccentricity ratio	e	0, 1	—
Shape of particles		spherical
Particle diameter	d_p	0.0000249 (24.9)	m (microns)
Particle density (dry density)	ρ_p	4193.92 (35.0)	kg/m³ (ppg)
Coefficient of restitution	ϵ	1.0	—
Number of CFD cells		84,102
CFD time-step	Δt_CFD	0.01	s
Physical time simulated	t_end	36	s

Assumptions

(i)
Flow of the liquid phase is in one direction (that is, axial), whereas that of the solid phase is in two directions (both axial and radial).
(ii)
The phases are incompressible; that is, the densities of the solid and liquid are constant.
(iii)
Interaction forces such as shear lift force, drag force, and pressure gradient force exist between the liquid and solid phase.
(iv)
Solid particles are spherical.
(v)
Solid particles are considered as Lagrangian phases.
(vi)
The liquid phase is a generalized power law (non-Newtonian) fluid.
(vii)
Isothermal and laminar flow are considered.

Boundary Conditions

(i)
No-slip condition at the walls.
(ii)
Inlet boundary conditions, that is, velocity inlet.
(iii)
Outlet boundary conditions, that is, pressure outlet.

4. Results and Discussion

4.1. 2D Model: Horizontal Pipe Section

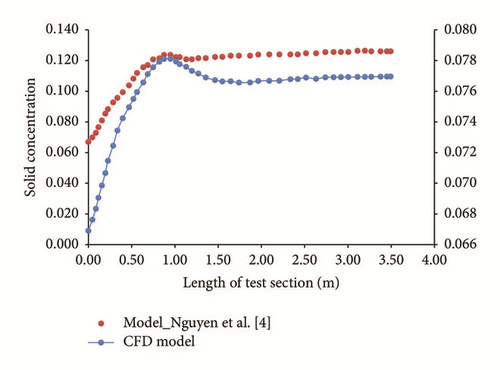
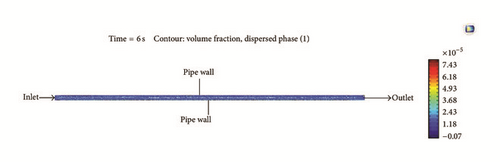
The 2D-CFD model is compared with the mathematical model of Nguyen et al. [4]. The variation of solid concentration in both the axial and lateral (radial) directions is shown in Figures 5 and 6 for an initial concentration of solid, C_o = 0.067; inlet fluid velocity, u = 0.1556 m/s; and deviation angle, θ = 90° (from vertical). Comparison between the CFD model and the mathematical model shows a reasonable match in the observed trend for the solid concentration distribution in both the axial and radial directions. However, it should be noted that there is variance in the observed magnitude of solid concentration. This is majorly attributed to the difference in the time taken to achieve the solution; for example, a simulation time of 1 s is equivalent to a physical time of many hours (or days). This is a plausible explanation as sufficient circulating time is required, in practice, to achieve considerable sedimentation (sag). The other possible reason(s) for the apparent discrepancy is/are unknown at the time. Note that the minimum time for the fluid to flow from inlet to outlet at a velocity of 0.1556 m/s is 23.5 s.

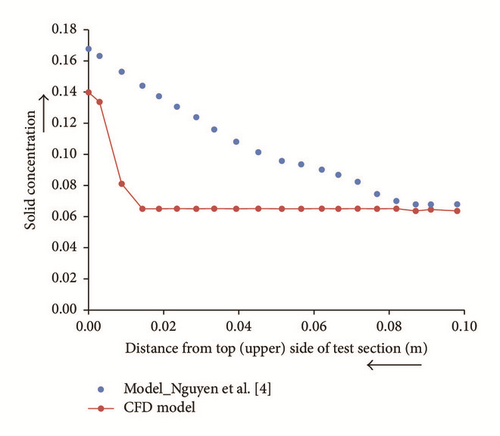
4.1.1. Solid Concentration Distribution

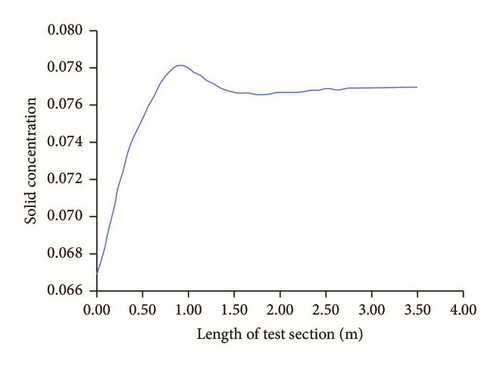
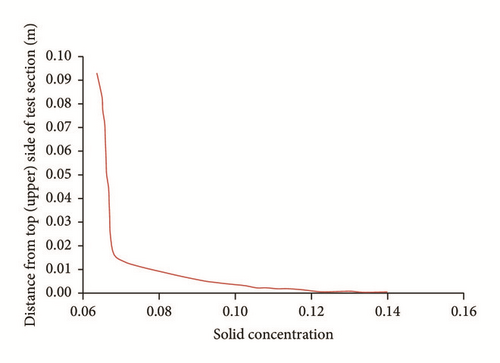
Initially, when t = 0 seconds, the solid concentration is C_o = 0.067. As time progresses, the concentration of solid increases in both the axial and lateral directions. The major increase in the concentration of solid occurs at the bottom of the pipe. Figure 7 displays that the concentration of solid increases rapidly near the inlet of the test section and thereafter appears to be constant. The concentration of solid at the upper section of the pipe does not decrease with time; it is nearly equal to the initial concentration of the solid (Figure 8). Additionally, Figure 8 shows that major increase in concentration of solid occurs at the bottom of the pipe.

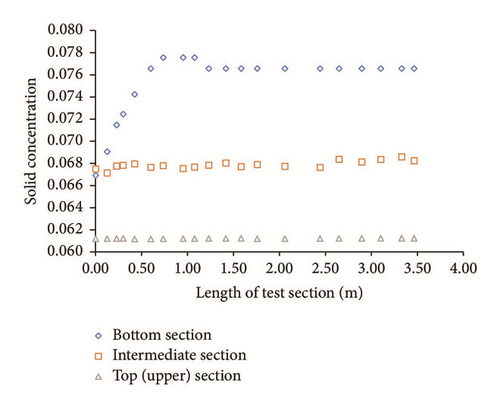
4.1.2. Barite Bed Characteristics

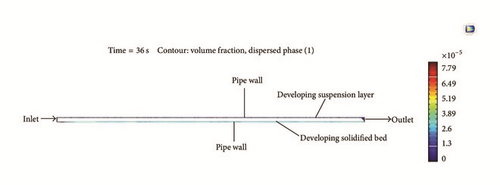
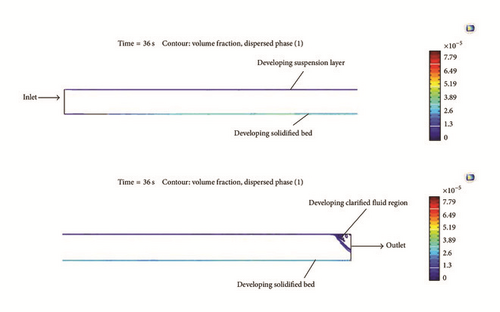
For low annular velocities (i.e., 0.1556 m/s), there is rapid formation of a barite bed at the bottom (lower) section of the pipe. The concentration of solid in this bed is not much greater than the concentration of solid in the fluid, which flows in the top (upper) side of the pipe. Put differently, the bed is actually the fluid with a greater concentration of solid and can be easily removed. This layer is what is referred to as the fluidized bed (see Figure 9, the intermediate section). As time progresses, the bed gets compacted and comes to be more solid. Note that the bed is called a “solidified bed” (Figure 9, the bottom section) when it has been compacted in a time period and cannot be dispatched by only raising annular velocity without initiating pipe rotation.

In brief, there exist three layers during the sedimentation of barite particles in the pipe: the clarified fluid layer (i.e., the fluid that flows upward), the fluidized bed, and the solidified bed layer. The dispersed phase volume fraction contour plots are shown in Figure 10. Additionally, Figure 11 shows the developing three regions during the accumulation of barite particle in the pipe. Note that the dispersed phase volume fraction, α_S, is related to the solid (dispersed) phase concentration by the equation

(44)

In this case, the initial dispersed phase volume fraction corresponds to

(45)

4.1.3. Mixture Viscosity

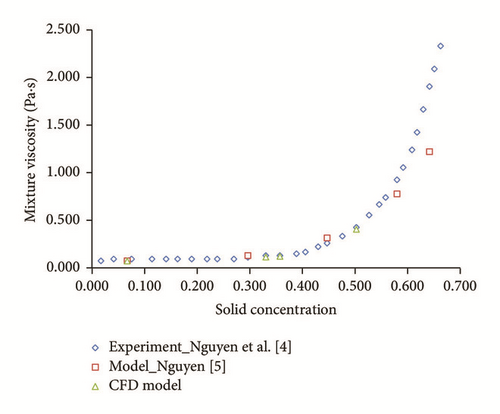
The relationship between continuous phase, dispersed phase, and mixture viscosity follows the correlations presented in (14a)–(14c). The influence of mixture viscosity on barite sedimentation in the pipe section is depicted in Figure 12. The outcomes of the CFD model show that the mixture viscosity is constant and satisfies Einstein’s formula. This is in agreement with the experimental and modelling data of Nguyen et al. [4] and Nguyen [5], up to a solid concentration of less than or equal to 0.4. Beyond a solid concentration of 0.4, the viscosity is a function of solid concentration.

4.2. 3D Model: Horizontal Annular Section

The minimum flow time from inlet to outlet at a velocity of 0.1524 m/s (lowest annular velocity) is 12 s and 2.4 s for a velocity of 0.762 m/s (highest annular velocity). The visualization of barite accumulation clearly illustrates the tendency for the particles to aggregate on the bottom (lower) side of the test section (particularly in the case of an eccentric annulus). This is for the case of a low annular velocity, in this case 0.1524 m/s (30 ft/min) with a stationary drill pipe. The redistribution of barite particles into the fluid stream, at a low annular velocity, is due to rotation of the drill pipe (Figure 13). The simulation outcome is a reasonable match with the experimental observations of Hashemian et al. [6, 7].

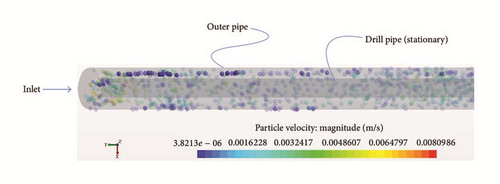
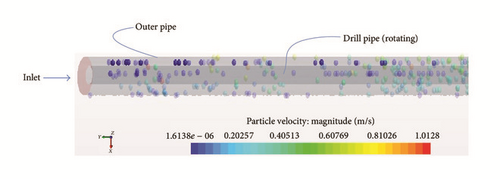
4.2.1. Influence of Drill Pipe Rotation on Barite Accumulation for a Concentric Annulus

Particles (barite particles) are injected into the fluid stream, at the inlet, at a mass flow rate of 0.055 kg/s. This configuration simulates the case of high particle concentration (i.e., α_P > 10⁻⁴). The inlet fluid velocity is 0.1524 m/s (in this case, the lowest annular velocity). Figure 14 shows the barite particle distribution at this low annular velocity and stationary drill pipe for a horizontal concentric annular test section. As can be observed from the sectional views on the right, barite accumulation in a concentric annulus is rather uniform (Figure 14(a)) and only has a slight nonuniform distribution (Figure 14(b)). Therefore, barite accumulation in a horizontal concentric annulus results into a smaller reduction in circulating drilling fluid density. Figure 15 shows the influence of drill pipe rotation at a low annular velocity on the barite accumulation in a horizontal concentric annulus. Observations from the sectional views on the right indicate that drill pipe rotation results into a uniform distribution of the barite particles in the concentric annular section. Overall, this has a slight effect on the barite accumulation. The simulation outcome is a reasonable match with the experimental observations of Hashemian et al. [6, 7].

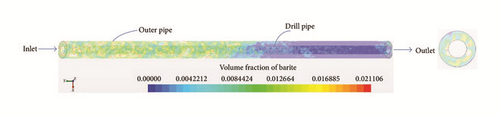
4.2.2. Combined Effect of High Annular Velocity and Drill Pipe Rotation on Barite Accumulation for a Concentric Annulus

Particles (barite particles) are injected into the fluid stream, at the inlet, at a particle flow rate which defines both the period of injection and the injection velocity. Additionally, this configuration simulates the case of low particle concentration (i.e., α_P < 10⁻⁴). The inlet fluid velocity is 0.762 m/s and drill pipe rotation speed is 50 rpm.

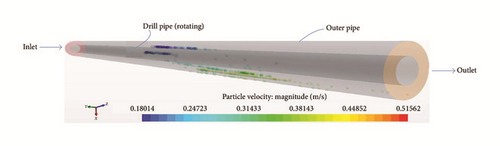
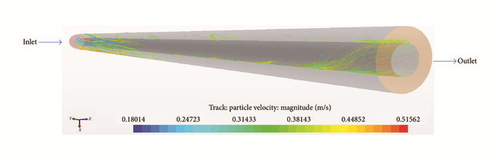
Initiated at the start of circulation: Figure 16 shows the barite particle behaviour in a horizontal annulus at a high inlet fluid velocity and drill pipe rotation. As can be observed, there is no tendency for barite accumulation in the test section. Even for the particles that are in the lower bottom, they are at a high velocity and thus there is no possibility for sedimentation. The simulation outcome is a reasonable match with the experimental observations of Hashemian et al. [6, 7]. Additionally, Figure 17 shows the particle tracks coloured by the velocity of particles. As can be observed, the particles further away from the inlet are at a higher velocity than the overall particles in the annular section, still indicating no possibility of barite accumulation.

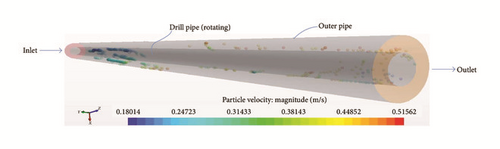
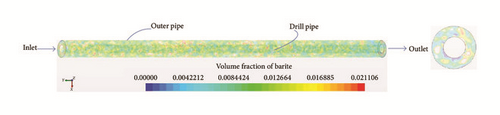
4.2.3. Combined Effect of High Annular Velocity and Drill Pipe Rotation on Barite Accumulation for an Eccentric Annulus

Initiated at the start of circulation: Figure 18 shows the barite particle behaviour in a horizontal annulus at a high inlet fluid velocity and drill pipe rotation. As can be observed, almost all particles in the test section, slightly further from the inlet, are at a relatively uniform higher velocity. In contrast to Figure 16(a), the combined effect of high annular velocity and rotation of drill pipe has a pronounced effect on barite accumulation in the eccentric scenario than in the concentric scenario.

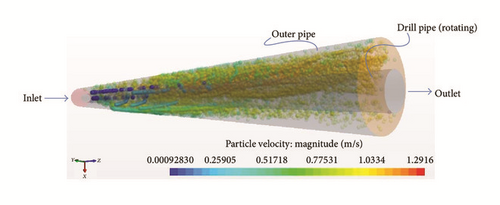
5. Limitations and Further Development

In as much as significant efforts have been made to address the key critical issues in numerical simulation of barite sag, some simplifications have also been made:

(i)
The 2D model configuration for the horizontal pipe does not account for pipe rotation. Additionally, the influence of mean velocity on dynamic barite sag is not accounted for.
(ii)
The 3D model configuration for the horizontal annulus does not account for different shapes and sizes of particles as it assumes uniform spherical particles. Different particle shapes and sizes can be introduced by employing different particle-shape models in the simulation and then observing the sag tendency.
(iii)
In the 3D model, only a qualitative analysis of the results is considered. At low particle concentrations, the quantitative results are comparable to those available in published literature and at very high particle concentrations; the model suffers from a convergence problem and thus does not produce reasonable results. Therefore, there is a need to perform a convergence improvement study so as to improve on the accuracy of the results and aid in the quantitative analysis of the results.
(iv)
In both models, no inclination angle other than 90° is considered. Inclination angles between 30° and 90° can be introduced in the simulation and the resulting sag tendency observed and analysed.
(v)
In the 3D model, based on the CFD-DEM approach, only a theoretical background for the governing equations (see the appendix) is provided and one stage of simulation successfully performed (see Figure 19); the implementation scheme employed is depicted in Figure 20. A complete simulation can be performed by using the implementation scheme in Figure 20 or Figure 21 to investigate the different aspects of barite sag under influencing factors, such as annular velocity, drill pipe rotation speed, and eccentric drill pipe.

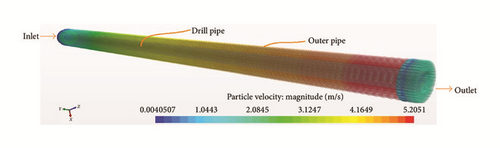
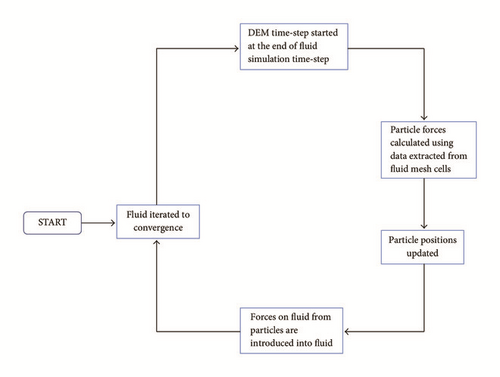
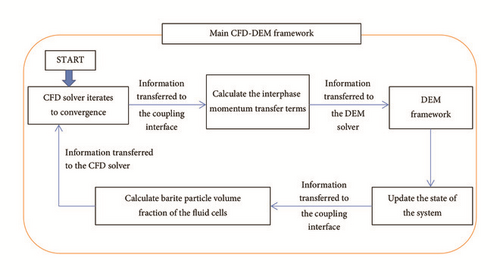
Nevertheless, the 3D model developed above, to the authors’ knowledge, is the first attempt to perform an independent numerical simulation to investigate dynamic barite sag in an annular section. Furthermore, the model based on the CFD-DEM approach is the first attempt to propose the use of the CFD-DEM method for the investigation of barite sag behaviour, keeping in mind that the system is a liquid-solid flow. Past researchers [15–18] have employed this approach in the study and analysis of other systems, but only considering gas-solid flows. The only exception is Zhao and Shan [19] and Akhshik et al. [20] who performed simulation of the behaviour of fluid-particle interactions for applications relevant to mining and geotechnical engineering [19] and the investigation of the effect of drill pipe rotation on cuttings transport behaviour [20].

6. Conclusions

A numerical simulation approach has been undertaken to investigate the different aspects of barite sag behaviour under influencing factors, such as annular velocity, drill pipe rotation speed, and eccentric drill pipe, as well as the rheology of drilling fluid, that is, Newtonian and non-Newtonian fluid. For the Newtonian fluid case, governing equations were built inside a 2D horizontal pipe geometry and the finite element method (FEM) utilized to solve the equation-sets whereas for the non-Newtonian fluid case, the governing equations were built inside a 3D horizontal annular geometry and the finite volume method (FVM) utilized to solve the equation-sets. Furthermore, it is worth noting that the drill pipe motion is modelled as a grid flux in the convective term, instead of a body force due to system rotation in the momentum equations.

The 2D-CFD model shows that the concentration of solid increases with time at the bottom (lower) section of the pipe. For a Newtonian fluid, which has viscosity of 0.062 Pa·s, the CFD model results indicate that, at low fluid inlet velocity (i.e., 0.1556 m/s), there is rapid formation of a barite bed at the bottom (lower) section of the pipe. Additionally, the model results show that there exist three layers during the sedimentation of barite particles in the pipe: the clarified fluid layer (i.e., the fluid that flows upward), the fluidized bed, and the solidified bed layer. There exists a critical solid concentration below which mixture viscosity is independent of solid concentration and beyond which the converse is true.

The developed 3D-CFD model outputs positive results in contrast to some experimentally reported observations in the study of the dynamic barite sag phenomenon:

(i)
For the case of low annular velocity (i.e., 0.1524 m/s), drill pipe rotation serves to disturb the apparent barite bed and redistribute the barite particles back into the flow stream.
(ii)
The effect of drill pipe rotation has a pronounced effect for the eccentric annulus compared to the concentric scenario.
(iii)
The combined effect of high annular velocity (i.e., 0.762 m/s) and drill pipe rotation (i.e., 50 rpm) results in a tremendous reduction in the barite sag occurrence. Still, the effect is more pronounced for the eccentric annulus than the concentric scenario.
(iv)
Maintaining the drilling fluid circulation at a high annular velocity and with rotating drill pipe ensures that no barite sag occurs.

Nomenclature

CFD:: Computational fluid dynamics
DEM:: Discrete element method
FDM:: Finite difference method
FEM:: Finite element method
FVM:: Finite volume method
2D:: 2-dimensional
3D:: 3-dimensional
Re:: Reynolds number
a_T:: Temperature shift factor
e:: Eccentricity ratio
C_d:: Drag coefficient
L:: Length of pipe/drill string length
d:: Diameter
D_p:: Diameter of pipe
D_h:: Diameter of hole
p:: Pressure
ρ:: Density
μ:: Viscosity
α:: Volume fraction
:: Shear rate
n:: Power law exponent
K:: Consistency factor
θ:: Deviation/inclination angle
ϵ:: Coefficient of restitution
ω:: Angular velocity.

Subscripts

n:: Normal
t:: Tangential
s:: Solid
p:: Particle
L:: Liquid
f:: Fluid.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work is financially supported by the Fundamental Research Funds for the Central Universities (Grant no. 16CX05019A) and the National Natural Science Foundation of China (Grant no. 51104171).

Appendix

Momentum Balance for the DEM Particle. The momentum balance for a DEM particle (barite) is derived from the momentum balance of the material particle (see (A.1))

(A.1)

where m_i is the mass of ith barite particle, F_S represents the forces acting on the surface of the particle, and F_B represents the body forces. These forces are in turn decomposed, as shown in (33a) and (33b).

The DEM modelling introduces extra body force representing interparticle interaction due to particle contacts with other particles and with mesh boundaries. Thus, (33b) becomes

(A.2a)

where

(A.2b)

Putting together the above considerations, (A.1) can then be written as

(A.3)

where

is the contact force acting from jth barite particle on ith barite particle, F_s denotes the shear lift force, and F_M represents the rotational lift force.

Note that the momentum transfer to the particle from the continuous phase is simply F_S. However, when two-way coupling is activated, F_S is accumulated over all the parcels and applied in the continuous phase momentum equation.

Besides the standard Lagrangian linear momentum equation, the DEM particle equations of motion incorporate angular momentum conservation equations:

(A.4)

where I_P is the particle moment of inertia, and ω_P is the particle angular velocity. Since the rotational motion is also affected by the drag torque, which is produced by the slip-rotation, (A.4) can be expressed as

(A.5)

where

and

are the torque vectors produced by the tangential and normal contact force acting from jth barite particle on the ith barite particle, respectively.

is the drag toque.

Contact Forces and Torques. Following the Hertz-Mindlin nonslip contact model [21], the forces between two spheres (barite particles), i and j, are described by the following set of equations (see Figure 22):

(A.6)

where F_n,ij denotes the normal contact force given as [21]

(A.7)

in which δ_n,ij is the normal overlap, E_eq is the equivalent Young modulus

, and R_eq is the equivalent radius

with E_i, v_i, d_i and E_j, v_j, d_j being Young’s modulus, Poisson ratio, and diameter of each element in contact.

denotes the normal damping force given by [21]

(A.8)

where m_eq is the equivalent barite particle mass

with m_i and m_j being the mass of each element in contact,

is the normal stiffness, v_n,ij is the normal component of the relative velocity of contact point, and ϵ_n is the normal coefficient of restitution.

The tangential component of the contact force, F_t,ij, is expressed as [21]

(A.9)

where

is the tangential stiffness in which G_eq is the equivalent shear modulus

, δ_t,ij is the tangential overlap, μ_s is the sliding friction coefficient, and v_t,ij is the relative tangential velocity of contact point.

The tangential damping force,

, is expressed as

(A.10)

Accordingly, the tangential torques acting on ith barite particle due to barite particle collision (jth barite particle) is expressed as [15]

(A.11)

and the torque to resist rolling action on ith barite particle due to barite particle collision (jth barite particle) is given as [15]

(A.12)

where r_ij is a vector from the center of mass of barite particle i to the contact point, μ_r is the rolling friction coefficient, and ω_ij is the relative angular velocity of barite particle i to particle j, (ω_i − ω_j). The torques

and

are generated by the tangential contact forces and the rolling friction, respectively.

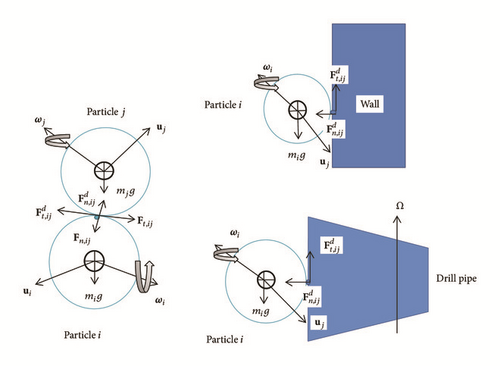
Note that, for particle-wall collisions, the formulas stay the same, but the wall radius and mass are assumed to be R_wall = ∞ and M_wall = ∞, so the equivalent radius is reduced to R_eq = R_particle and M_wall = M_particle.

Drag Force and Drag Torque. The equation for the drag force is as defined in (34). The drag coefficient is given by the Gidaspow drag coefficient method, which is a combination of the Wen-Yu and Ergun methods where a cutoff void fraction determines the point at which one method switches to the other. Equation (A.13) (Wen-Yu) and (A.14) (Ergun) are the relevant method equations:

(A.13)

Otherwise:

(A.14)

where α_f is the void fraction, α_min is the cutoff void fraction, and Re_P is the particle Reynolds number and is given as

(A.15)

Note that, during implementation, α_min is user-defined and also the exponent in (A.13) can be user-defined.

Drag torque reduces the difference in the rotational differences between a particle and the fluid in which it is immersed. The drag is a torque applied to a DEM particle [14]

(A.16)

where C_DR is the rotational drag coefficient, d_p is the particle diameter, and Ω is the relative angular velocity of the barite particle to the fluid (Ω = (1/2)∇×u_f − ω_p).

The rotational drag coefficient, C_DR, is defined as [14]

(A.17)

in which the Reynolds number of barite particle rotation is given by

(A.18)

Pressure Gradient Force. The equation for pressure gradient force is as defined in (35).

DEM Lift Forces. Lift forces in DEM simulations can arise from particle spin, particle shear, or both. Thus, lift forces are taken to mean forces normal to the particle velocity; they are not necessarily forces in the upward direction.

(a) Particle Shear Lift Force. This force applies to a particle moving relative to a fluid where there is a velocity gradient in the fluid orthogonal to the relative motion; it is as defined in (37)–(41).

(b) Particle Spin Lift Force. This force applies to a spinning particle moving relative to a fluid; it is given by [14]

(A.19)

where C_LR is the rotational lift coefficient and is given by [14]

(A.20)

where Re_R is as defined in (A.18).

Note that (A.20) is a 3D version; the 2D equivalent has a term .

References

1 API, API Recommended Practice 13D - Rheology and Hydraulics of Oil-Well Fluids, 2009, API, DC, Washington, USA.
Google Scholar
2 Paslay P., Sathuvalli U. B., and Payne M. L., A phenomenological approach to analysis of barite sag in drilling muds, Proceedings of the SPE Annual Technical Conference and Exhibition, November 2007, Anaheim, Calif, USA., 1–11, https://doi.org/10.2118/110404-MS.
10.2118/110404-MS
Google Scholar
3 Dye W., Hemphill T., Guster W., and Mullen G., Correlation of ultralow-shear-rate viscosity and dynamic barite sag, SPE Drilling and Completion. (2001) 16, no. 1, 27–34, https://doi.org/10.2118/70128-PA, 2-s2.0-0035266080.
10.2118/70128-PA
Web of Science® Google Scholar
4 Nguyen T. C., Yu M., and Takach N., Predicting dynamic barite sag in newtonian oil-based drilling fluids, Proceedings of the SPE Annual Technical Conference and Exhibition, October 2009, New Orleans, LA, USA, https://doi.org/10.2118/124137-MS.
10.2118/124137-MS
Google Scholar
5 Nguyen T. C., Predicting Dynamic Barite Sag in Oil-Based Drilling Fluids [PhD Dissertation], 2009, ProQuest LLC, Ann Arbor, Mich, USA, https://doi.org/10.2118/124137-MS.
10.2118/124137-MS
Google Scholar
6 Hashemian Y., Miska S., Yu M., Ozbayoglu E., Takach N., and McLaury B., Experimental study and modelling of barite sag in annular flow, Journal of Canadian Petroleum Technology. (2014) 53, no. 6, 365–373, 2-s2.0-84911395666, https://doi.org/10.2118/173189-PA.
10.2118/173189-PA
Google Scholar
7 Hashemian A. Y., Miska S., Yu M., and Ozbayoglu E., Numerical simulation and experiments of barite sag in horizontal annulus, American Journal of Numerical Analysis. (2014) 2, no. 1, 14–19.
Google Scholar
8 Kulkarni S. D. et al., Modeling Real-Time Sag in the Wellbore, Proceedings of the IADC/SPE Drilling Conference & Exhibition, March 2016, Fort Worth, Tex, USA.
Google Scholar
9 Crowe C. T., Sommerfeld M. et al., Multiphase Flows with Droplets and Particles, 2012, 2nd edition, CRC Press, Boca Raton, Fla, USA.
Google Scholar
10 Van Wachem B. G. M., Schouten J. C., Van den Bleek C. M., Krishna R., and Sinclair J. L., Comparative analysis of CFD models of dense gas-solid systems, AIChE Journal. (2001) 47, no. 5, 1035–1051, 2-s2.0-0035335342, https://doi.org/10.1002/aic.690470510.
10.1002/aic.690470510
CAS Web of Science® Google Scholar
11 Enwald H., Peirano E., and Almstedt A.-E., Eulerian two-phase flow theory applied to fluidization, International Journal of Multiphase Flow. (1996) 22, no. 1, 21–66, 2-s2.0-0030367828, https://doi.org/10.1016/S0301-9322(96)90004-X, Zbl1135.76409.
10.1016/S0301-9322(96)90004-X
CAS Web of Science® Google Scholar
12 Saffman P. G., The lift on a small sphere in a slow shear flow, Journal of Fluid Mechanics. (1965) 22, no. 2, 385–400, https://doi.org/10.1017/s0022112065000824, Zbl0218.76043.
10.1017/S0022112065000824
Web of Science® Google Scholar
13 CD-ADAPCO, Star-CCM+ User Guide, 2016, CD-ADAPCO, New York, NY, USA.
Google Scholar
14 Sommerfeld P. D. I., Theoretical and Experimental Modelling of Particulate Flows: Overview and Fundamentals, 2000.
Google Scholar
15 Kuang S. B., Yu A. B., and Zou Z. S., Computational study of flow regimes in vertical pneumatic conveying, Industrial and Engineering Chemistry Research. (2009) 48, no. 14, 6846–6858, 2-s2.0-67849118738, https://doi.org/10.1021/ie900230s.
10.1021/ie900230s
CAS Web of Science® Google Scholar
16 Smuts E. M., Deglon D. A. et al., Methodology for CFD-DEM modelling of particulate suspension rheology, Proceedings of the 9th International Conference on CFD in the Minerals and Process Industries, 2012, Melbourne, Australia, 1–7.
Google Scholar
17 Hager A., Kloss C., Pirker S., and Goniva C., Parallel open source CFD-DEM for resolved particle-fluid interaction, Journal of Energy and Power Engineering. (2013) 7, no. 9, 1705–1712.
Google Scholar
18 Hager A., Kloss C., Pirker S., and Goniva C., Parallel resolved open source CFD-DEM: method, validation and application, Journal of Computational Multiphase Flows. (2014) 6, no. 1, 13–28, https://doi.org/10.1260/1757-482X.6.1.13, 2-s2.0-84897838316.
10.1260/1757-482X.6.1.13
Google Scholar
19 Zhao J. and Shan T., Coupled CFD-DEM simulation of fluid-particle interaction in geomechanics, Powder Technology. (2013) 239, 248–258, 2-s2.0-84874521713, https://doi.org/10.1016/j.powtec.2013.02.003.
10.1016/j.powtec.2013.02.003
CAS Web of Science® Google Scholar
20 Akhshik S., Behzad M., and Rajabi M., CFD-DEM approach to investigate the effect of drill pipe rotation on cuttings transport behavior, Journal of Petroleum Science and Engineering. (2015) 127, 229–244, 2-s2.0-84923013580, https://doi.org/10.1016/j.petrol.2015.01.017.
10.1016/j.petrol.2015.01.017
CAS Web of Science® Google Scholar
21 Di Renzo A. and Di Maio F. P., Comparison of contact-force models for the simulation of collisions in DEM-based granular flow codes, Chemical Engineering Science. (2004) 59, no. 3, 525–541, https://doi.org/10.1016/j.ces.2003.09.037, 2-s2.0-0842344539.
10.1016/j.ces.2003.09.037
CAS Web of Science® Google Scholar

Citing Literature

All articles

Numerical Simulation of Barite Sag in Pipe and Annular Flow

Abstract

1. Introduction

2. Mathematical Approach

2.1. Horizontal Pipe Section

2.1.1. Mass Balance

2.1.2. Momentum Balance

2.1.3. Dispersed Phase Viscosity

2.1.4. Interphase Momentum Transfer

2.1.5. Dilute Flows

2.1.6. Solid Pressure

2.2. Horizontal Annular Section

2.2.1. Governing Equations for Fluid Flow

2.2.2. Governing Equations for Particle Flow

3. Model Configuration

3.1. 2D Model: Horizontal Pipe Section

3.2. 3D Model: Horizontal Annular Section

4. Results and Discussion

4.1. 2D Model: Horizontal Pipe Section

4.1.1. Solid Concentration Distribution

4.1.2. Barite Bed Characteristics

4.1.3. Mixture Viscosity

4.2. 3D Model: Horizontal Annular Section

4.2.1. Influence of Drill Pipe Rotation on Barite Accumulation for a Concentric Annulus

4.2.2. Combined Effect of High Annular Velocity and Drill Pipe Rotation on Barite Accumulation for a Concentric Annulus

4.2.3. Combined Effect of High Annular Velocity and Drill Pipe Rotation on Barite Accumulation for an Eccentric Annulus

5. Limitations and Further Development

6. Conclusions

Nomenclature

Subscripts

Conflicts of Interest

Acknowledgments

Appendix

References

Citing Literature

Figures

References

Related

Information