The soft mode dynamical model has been used to study dielectric properties and ultrasonic attenuation in KDP-type ferroelectric crystals. The model Hamiltonian proposed by Blinc and Zeks has been modified by considering lattice anharmonicity up to fourth-order. The correlations appearing in the dynamical equation have been evaluated using double-time thermal retarded Green’s functions method and Dyson’s equation. Without any decoupling, the higher order correlations, appearing in the dynamical equation, have been evaluated using the renormalized Hamiltonian. The expressions for collective frequencies, width, dielectric constant, ultrasonic attenuation, and tangent loss have been calculated. The dielectric properties and ultrasonic attenuation strongly depend on the relaxational mode behavior of stochastic motion of H₂PO₄ group in KDP-type ferroelectrics. By fitting model values of physical quantities, the temperature dependence of and for different value of four-body coupling coefficient and dielectric constant and loss tangent has been calculated. The calculated and observed results have been found in good agreement.

1. Introduction

The oscillations of atoms in solids are responsible for different characteristics, such as specific heat, optical, dielectric, and electrical properties. The anharmonicity in solids is responsible for existence of thermal expansion, temperature variation of elastic constants, lattice thermal conductivity, deviation of specific heat from Dulong-Petit law at high temperature, existence of ferroelectricity in certain materials, and so forth. Many attempts have been made theoretically and experimentally to find the explanation of these phenomena in terms of anharmonicity. Extensive reviews [1, 2] are available discussing the contribution of anharmonicity to various properties of crystals.

In order-disorder type ferroelectrics, as Potassium Dihydrogen Phosphate (KH₂PO₄), the transition is associated with the tunneling of proton through a barrier between two positions of minimum potential energy in double well potential in the hydrogen bond at the transition temperature [3]. Busch [4] was the first to show that KDP (KH₂PO₄) exhibits a phase transition at low temperature. KDP is prototype of a family of crystals with bridging hydrogen bonds and its physical properties have been extensively studied [3, 5–10].

Kaminow and Damen [11] first observed the soft mode associated with the ferroelectric phase transition of the KDP-type crystal at 122.3 K by measuring the low frequency Raman scattering in x(yx)y configuration. Since then B₂(z) soft mode which is connected to the susceptibility along the crystalline c-axis through the Lyddane-Sachs-Teller relation [12] has been extensively studied by Scott [13] and interpreted using the pseudospin model [14–16] and its modifications in [3, 17]. In these theories, such a particular mode of proton motions along hydrogen bonds in a-b plane is coupled to other ion modes, bearing an electrical dipole moment along c-axis is considered to play an essential role for the ferroelectric transition, and therefore little attention has been paid to the modes other than B₂(z) soft mode. In KDP crystal, however, there are four tunneling protons in a primitive unit cell of the paraelectric (hereafter referred to as PE) phase and consequently four normal modes are belonging to B₂(z), a doubly degenerate E(x, y), and A₂ modes [18]. E(x, y) mode, which is both infrared and Raman active, provides valuable information, because this mode and B₂(z) mode reflect the nature of collective proton motion which triggers the phase transition, and, moreover, in contrast to B₂(z), it is directly related to the polarization along the crystalline a-axis.

At first, Pak [19] employed Green’s function methods in the order-disorder type ferroelectrics and, however, did not consider the anharmonic interactions. The phonon anharmonic interactions have been found very important in explaining dielectric, thermal, and scattering properties of solids by many authors [6–9, 20, 21] in the past. Pak’s theory was further developed by Ramakrishnan and Tanaka [22], who calculated the excitation spectrum of the system but did not consider the anharmonic interactions. Their attempt, however, established the superiority of Green’s function method over the other methods. Ganguli et al. [23] modified Ramakrishnan and Tanaka theory by considering anharmonic interaction. Their treatment explains many features of order-disorder ferroelectrics. However, due to insufficient treatment of anharmonic interactions, they could not explain quantitatively good results and could not describe some very interesting properties, like dielectric properties, ultrasonic attenuation, relaxation rate, and so forth.

In the present study, the four-particle cluster model Hamiltonian with the phonon anharmonicity up to fourth-order has been taken to theoretical study of dielectric properties and ultrasonic attenuation in KDP-type crystals, using double time Green’s functions method and Dyson’s equation. Proton Green’s function and phonon Green’s function have been solved for the collective system. Expressions for collective mode frequency shifts, widths, transition (Curie) temperature, and the expectation value of the proton collective mode components at site q (,) have been derived and discussed in KDP-type crystals. By fitting model values of physical quantities, the temperature dependence of and for different value of four-body coupling, dielectric constant, and loss tangent has been calculated. The calculated and observed results have been found in good agreement.

2. The Model Hamiltonian and Green’s Function

For KDP crystal, the four-particle cluster model Hamiltonian [24] along with third- and fourth-order phonon anharmonic interaction terms is expressed as

()

where the first two terms constitute the original pseudospin model Hamiltonian and the third is the quadrupole contribution (the four-body interaction).

is the tunneling operator which measures the tunneling power of the proton between the hydrogen double well, Ω the tunneling frequency, and

the half of the difference of the occupation probabilities for the proton in the two equilibrium positions of hydrogen bond.

is the two-body coupling coefficient and is the same for every pair of protons in KDP and the four-body coupling coefficient, and

refers to the four hydrogen bonds in the PO₄ group in KDP. In the last fourth terms ω_k is bare phonon frequency, A_k and B_k are displacement and momentum operators,

is proton-lattice interaction term, and V₃ and V₄ are the third- and fourth-order anharmonic coefficients.

2.1. Collective Proton Wave Width and Shift

The correlations appearing in the proton response function can be evaluated using double time thermal retarded Green’s function [25] using the symmetrical decoupling scheme, after applying Dyson’s treatment:

()

where the angular brackets denote the average over the large canonical ensemble and θ(t) is the Heaviside step function having properties

()

Differentiating (2) twice with respect to time “t,” using Hamiltonian (1) taking Fourier transformation, one obtains

()

where E(ω) is higher order Green’s functions:

()

with

()

E(ω) is calculated by differentiating (5) twice with respect to “t” using Hamiltonian (1) and then taking Fourier transformation; one obtains

()

and higher order Green’s functions

()

with

()

Substituting the value of

from (7) into (4) and using Dyson’s equation, one obtains

()

where the renormalized frequency is

()

with

Higher order Green’s functions

are calculated using symmetrical decoupling scheme, the cross combinations are not considered because they do not contribute significantly, and (10) can be written as

()

where

is the proton renormalized frequency of the coupled system, which on solving self-consistently takes the form

()

The real and imaginary parts of (12) are obtained by using the formula

()

Δ_s(q, ω) and Γ_s(q, ω) represent collective proton mode frequency shift and width given as

()

with

()

2.2. Collective Phonon Half Width and Mode Frequency Shift

The acoustic phonon frequency width and shift are obtained analogously from acoustic phonon Green’s function:

()

Differentiating (18) twice with respect to time “t,” using Hamiltonian (1) taking Fourier transformation, one has

()

where

()

Higher order Green’s functions are evaluated without any decoupling and using renormalized Hamiltonian. Putting the evaluated value of higher order Green’s function in (19), one gets

()

The real part of P(q, ω) is obtained by using (14) and the collective mode frequency shift is obtained as

()

with

where

is occupation number and β = (k_BT) ⁻¹, k_B being Boltzmann’s constant and T being the absolute temperature. Calculating (20) self-consistently and approximating, the collective mode frequency is given by

()

Equation (22a) is obtained using model Hamiltonian (1), and (22b) and (22c) are obtained without decoupling and using the renormalized Hamiltonian

()

The imaginary part of P(q, ω) is obtained by using (19) and collective phonon half width is obtained as

()

2.3. Order Parameter Values of , , and

The expectation values of the proton collective mode component at site “q” have been obtained by Blinc and Zeks [26] as

()

In PE phase (T > T_c), (26) represent a system of 3N equations for the average value of the collective mode components. The solution of this system will, however, be stable only if they minimize the free energy, that is, if

, and so

()

in the ferroelectric phase (T < T_c) [27]. Consider

()

2.4. Dielectric Constant and Tangent Loss

Following Kubo [28] and Zubarev [25] the real part of dielectric constant is given by

()

where μ is the effective dipole moment per unit cell and N is the number of unit cells in the sample.

The dielectric loss (tan⁡δ) is defined as the ratio of imaginary and real parts of dielectric constant and can be written as

()

Thus retarded phonon Green’s function is enough to determine the dielectric constant and loss tangent. Using (29) and (22), the real part of dielectric constant can be written as

()

For the experimental range of frequencies

(as well as ωτ_p ≪ 1 for KDP crystals), (31) can be reduced to

()

where

is given by (20) and

is given by (20a).

The tangent loss is given by

()

where Γ_p is given by (25). For

, (33) becomes

()

where α is harmonic and defect contribution, β and γ are due to three and four phonon anharmonic interaction terms of the lattice.

2.5. Ultrasonic Attenuation

The expression for ultrasonic attenuation constant is given by

()

where damping constant is given by (17) and C_μ(q) is the ultrasonic velocity. For small q limit, we obtain the collective proton mode frequency width, for

, from (17) expressed as

()

where τ_p is polarization relaxation time and is given by Litov and Garland [29] as

()

Similar expressions for frequency shift and ultrasonic attenuation have been derived by Zurek [30], using the Landau-Khalatnikov theory. If the collective mode damping is neglected, a discontinuity in sound velocity is obtained at T = T_c, since

is proportional to (T_c − T) for T ≤ T_c. the effect of factor

is to smooth out the discontinuity.

The ultrasonic attenuation peaks for ωτ_p≅1 and ω_q (i.e.,

) goes to zero as T → T_c. For temperature such as ωτ_p ≪ 1, the attenuation will have the form

()

where

()

The dependence of ultrasonic attenuation on applied frequency (ω) and the collective mode frequency (

) may be expected to apply also to the displacive phase transition [31], for which the coupling is linear to the strain and bilinear to the soft optical normal mode coordinates, independent of whether the phonon instability occurs at q = 0, q = q_k, or at a general point in the Brillouin zone. Though the linear dependence of (

) on (T − T_c) has been assumed for T≅T_c, this dependence presumably breaks down sufficiently close to T_c.

2.6. Transition Temperature

In the PE phase

, and the stability limit of PE phase is determine by the temperature where

approaches zero as T → T_c. Consider

()

using (13), where

()

with effective exchange coupling constant

()

as well as transition temperature

()

3. Comparison with Experiments and Discussion

3.1. Numerical Calculations

The parameters in our calculation are listed in Table 1. The calculated values of and for KDP-type crystals for different values of four-body coupling coefficient (J^′), collective phonon mode frequency , transverse dielectric constant {ε_a(o)}, observed dielectric constant {ε_c(o)}, and tangent loss along a-axis (tan⁡δ_a) and c-axis (tan⁡δ_c) for KDP-type crystals are listed in Tables 2 and 3. Their variations with temperature are shown in Figures 1–4.

Table 1. Blinc-de Gennes model parameters for KDP-type crystals as given by Ganguli et al. [23].

Ω (cm⁻¹)	J (cm⁻¹)	J^′ (cm⁻¹)	V_ik (cm⁻¹)	ω_k (cm⁻¹)	μ × 10¹⁸ (cgs)	T_c (K)	V/kT_c
82	334	440	25.56	153	1.8	123	0.299

Table 2. Calculated values of

and

for KDP crystal for different values of four-body coupling coefficient (J^′).


Temperature (K)	J^′ = J/3	J^′ = 4J/3	J^′ = 7J/3	J^′ = J/3	J^′ = 4J/3	J^′ = 7J/3
			Present study			Present study
20	0.500	0.499	0.499	0.454	0.369	0.311
40	0.498	0.499	0.499	0.455	0.369	0.311
60	0.459	0.481	0.498	0.460	0.376	0.312
80	0.257	0.278	0.487	0.482	0.446	0.317
100	0.137	0.143	0.454	0.489	0.479	0.332
120	0.102	0.104	0.409	0.490	0.485	0.354
122	0.100	0.100	0.403	0.491	0.486	0.357
123	0.000	0.000	0.400	0.492	0.492	0.358
125	0.000	0.000	0.398	0.484	0.484	0.449
130	0.000	0.000	0.389	0.468	0.468	0.457
135	0.000	0.000	0.373	0.446	0.446	0.443
140	0.000	0.000	0.352	0.426	0.426	0.436
145	0.000	0.000	0.320	0.408	0.408	0.410
150	0.000	0.000	0.300	0.396	0.396	0.392

Table 3. Calculated values of

, and tan⁡δ_c for KDP-type crystals.

Temperature (K)	Collective phonon mode frequency (cm⁻¹) (present study)	Transverse dielectric constant ε_a(0) (present study)	Observed dielectric constant ε_c(0) (present study)	Loss tangent along the a-axis (tan⁡δ_a) (present study)	Loss tangent along the c-axis (tan⁡δ_c) (present study)
125	45.65	63	35741	0.004	0.067
130	57.04	62	6144	0.00398	0.035
135	58.69	61	2286	0.00397	0.0261
140	63.04	60	874	0.00396	0.0255
145	65.91	59	486	0.00365	0.0250

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Temperature dependence of and for KDP-type crystal for different values of J^′. (a) J^′ = J/3, (b) J^′ = 4J/3, and (c) J^′ = 7J/3 (present study).

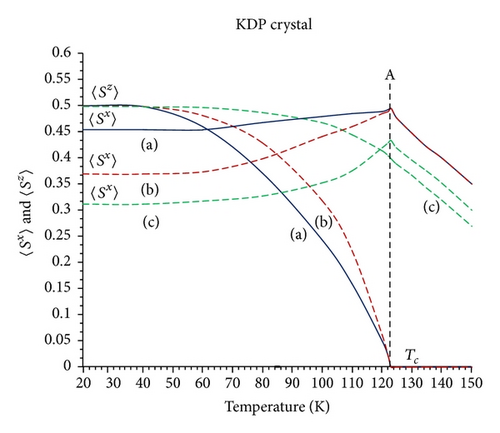
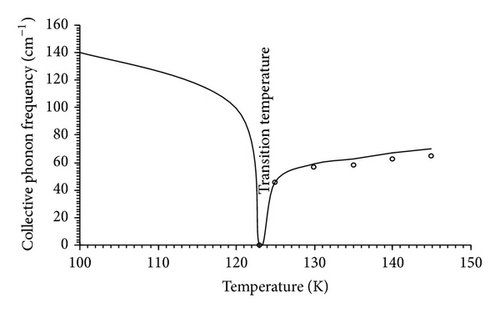
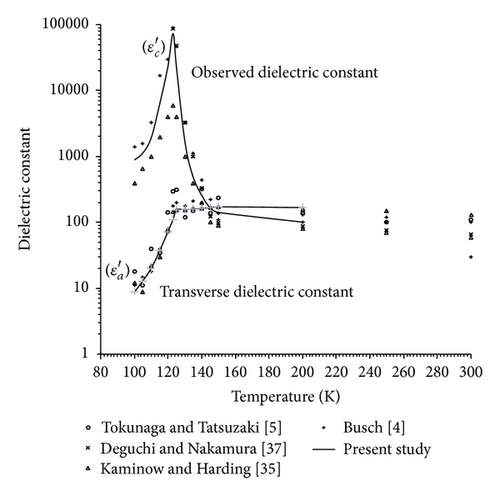
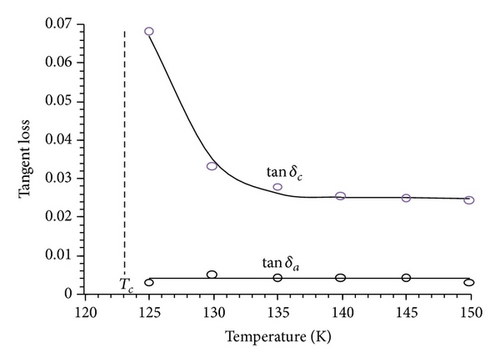
3.2. Temperature Dependence of and for KDP-Type Crystal for Different Values of J^′

Using Blinc-de Gennes model parameter values for KDP-type ferroelectrics crystals as given by Ganguli et al. [23], putting these values into (27) and (28), we have calculated temperature dependence of and for KDP-type crystal for different values of J^′, and variation is shown in Figure 1.

In Figure 1, the curve (a) is the case of J^′ = J/3 < 4J/3, curve (b) is J^′ = 4J/3 < 7J/3, and curve (c) is J^′ = 7J/3 > 4J/3. In curves (a) and (b) the value of increases to the saturated value 0.5 from zero, when temperature decreases from transition temperature. That is the case of second-order phase transition. But in curve (c) the change of with the temperature starts from a nonzero value at point “A”; that is to say, when temperature decreases increases to the saturation value from the finite value of . This is the case of first-order phase transition. The temperature at point “A” is transition temperature, and the value of at “A” is the discontinuity of . The value of decreases when temperature decreases in the ferroelectric phase. On the other hand, in PE phase the value of decreases when temperature increases from transition temperature.

3.3. Temperature Dependence of Collective Phonon Mode Frequency in PE Phase

Using (23) and (41) and model parameters values from Table 1, the temperature variation of collective phonon mode frequency in PE phase is shown in Figure 2. In the PE phase the temperature dependence of normalized collective phonon frequency enables one to calculate the transition temperature (44), as well as effective exchange coupling constant (43), which increases due to proton-phonon coupling and decreases due to anharmonic interactions. By fitting model values of physical quantities, temperature dependence of collective phonon mode frequency has been calculated which compares well with experimental results of Baumgartner [32] and Choi and Lockwood [33].

3.4. Temperature Dependence of Dielectric Constant

Putting calculated values for different temperature into (32) we obtain dielectric constant for KDP-type crystals. mode corresponds to transverse E(x, y) mode, which is responsible for the observed transverse dielectric properties of KDP. In the simplest approximation can be written (), where K₁ and K₂ are temperature independent parameters. The results for transverse dielectric constant obtained from the integrated intensity of Raman spectroscopy [34] and those measured by Busch [4] and Kaminow and Harding [35] are shown in Figure 3, together with the theoretical results of Havlin et al. [36]. This indicates that low frequency {E(x, y) mode} is closely related to the macroscopic dielectric constant . This also suggests that the E-mode Raman spectrum originates neither from the second-order Raman scattering nor from the density of states due to the local disorder above T_c but from one of the collective modes at the centre of the Brillouin zone. It should be mentioned here that the low frequency E-mode continuum appears also in a deuterated KDP (DKDP), although the intensity is about one-third of that of KDP, which indicates the possibility that the spectrum is due to the hydrogen collective motion. Using (23) for mode, it can be seen that the E-mode collective hydrogen motion has characteristics damping factor which slowly increases as the temperature approaches T_c, while for that of soft mode the damping factor slowly decreases down to a finite value, which agrees with the observations of Kaminow and Damen [11].

The present results agree with the behaviour of the observed E-mode Raman spectrum in the following aspects: (i) does not change appreciably as T → T_c in PE phase, (ii) is weakly dependent on temperature, and (iii) because of the factor () in the numerator of (31), the susceptibility derived changes the corresponding spectrum from a simple overdamped form to a more flat one, like the E-mode Raman spectrum of KH₂PO₄ [27].

The observed dielectric constant

of KH₂PO₄ along c-axis is shown in Figure 3. The

mode may be assigned for the observed temperature dependence of

. As from (41)

, the real part of the dielectric constant associated with this mode, from (32), can be expressed as

()

which explains the Curie-Weiss behaviour of dielectric constant along the c-axis of KH₂PO₄ crystal in the PE phase observed by Deguchi and Nakamura [37], Busch [4], and Kaminow and Harding [35], shown in Figure 3. For temperature T → T_c,

tends to maximum value, which is consistent with the theory of Hill and Ichiki [38] for TGS and KDP crystals, while Mason monodisperse theory [39] gives

as T → T_c. The origin of this difference in the temperature dependence of

is easily traced back in monodisperse theory, and the critical slowing down of the relaxation time has a dominant effect over the Curie-Weiss law of static dielectric constant, while the Hill-Ichiki theory of distribution function of relaxation time makes contribution to finite τ ≠ 0 to

more dominant.

There are actually, however, many cases in which takes a minimum of finite value at T = T_c being neither zero as in Mason’s theory nor maximum as in Hill and Ichiki theory.

3.5. Temperature Dependence of Tangent Loss

The tangent loss is associated with damping parameter (25). Damping can be understood as the creation of a virtual polarization mode excited by the transverse electromagnetic radiation and its subsequent decay into the real phonons by scattering from crystal defects, higher order phonon anharmonicities, and so forth. At higher temperature the loss deviates from the Curie-Weiss type behaviour and increases linearly with temperature. This behaviour suggests that at higher temperatures the phonon anharmonicity contributes significantly to the observed loss.

The calculated values of tangent loss from (33) and (34) and experimental result of Kaminow and Harding [35] are shown in Figure 4 and given in Table 3. The loss was calculated at 9.2 GHz because experimental data is available only at that frequency range. The theoretical results of the present study are in good agreement with experimental results of Kaminow and Harding [35]. The temperature dependence of loss does not appear to be exponential. Thus, third- and fourth-order anharmonicity may be responsible for the observed behaviour of loss tangent. In the microwave frequency rage, an increase in frequency is followed by an increase in transverse and longitudinal dielectric loss tangent. The loss decreases with increase in temperature for KDP-type crystals, in their PE phase. This shows Curie-Weiss type behaviour of the dielectric loss tangent.

In this paper the four-particle cluster model Hamiltonian with the anharmonic contributions up to fourth-order has been taken into consideration in study of dielectric properties and ultrasonic attenuation in KDP-type ferroelectric crystals. Using double time thermal Green’s function method and Dyson’s equation the collective mode frequencies and widths have been calculated. These parameters lead to the expressions for the dielectric constant and loss tangent. The observed dielectric properties have been explained in terms of present study. The expressions for dielectric constant and loss tangent have been derived and compared with the experimental results. Using Blinc-de Gennes model parameter values given by Ganguli et al. [23] we have calculated temperature variations of these quantities for KDP- type crystals. It is observed that these results are in good agreement with each other and with the results obtained by other methods. The present results reduce to the results of others [22, 23, 40] if the width and shift are neglected. Only Ganguli et al. [23] modified the Ramakrishnan and Tanaka theory by considering anharmonic interaction. Their treatment explains many features of order-disorder ferroelectrics. However, due to insufficient treatment of anharmonic interactions, they could not obtain quantitatively good results and could not describe some very interesting properties, like dielectric properties, acoustic attenuation, and so forth.

Thus, from the present study, it is concluded that the consideration of four-cluster Hamiltonian along with the third- and fourth-order anharmonicities for the KDP-type ferroelectrics leads to the renormalization and stabilization of the relaxational soft mode and the renormalization of the pseudospin exchange interaction constant. The decoupling of the correlations appearing in the dynamical equation after applying Dyson’s equation results in shift in frequency and facilitates the calculation of damping parameter, which is related to the loss tangent. The anomalous behaviour in order-disorder KDP-type ferroelectrics finds explanation by the consideration of collective proton-phonon interaction and third- and fourth-order anharmonicities in the four-particle cluster Hamiltonian. The dielectric properties and ultrasonic attenuation strongly depend on the relaxational mode behaviour of stochastic motion of H₂PO₄ group in KDP-type ferroelectrics.

Competing Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

References

1 Semwal B. S. and Sharma P. K., Thermal conductivity of an anharmonic crystal, Physical Review B. (1972) 5, no. 10, 3909–3914, https://doi.org/10.1103/physrevb.5.3909, 2-s2.0-0013065821.
10.1103/PhysRevB.5.3909
Web of Science® Google Scholar
2 Semwal B. S. and Sharma P. K., Thermal conductivity of an isotopically disordered harmonic crystal, Journal of Mathematical Physics. (1974) 15, no. 5, 648–653, 2-s2.0-36849110801.
10.1063/1.1666701
Web of Science® Google Scholar
3 Kobayashi K. K., Dynamical theory of the phase transition in KH2PO4-type ferroelectric crystals, Journal Physics Society Japan. (1968) 24.
Web of Science® Google Scholar
4 Busch G., Neue seignette-elektrika, Helvetica Physica Acta. (1938) 11, no. 4.
Google Scholar
5 Tokunaga M. and Tatsuzaki I., Light scattering spectra of polarization fluctuations and models of the phase transition in KDP type ferroelectrics, Phase Transitions. (1984) 4, no. 2, 97–155, https://doi.org/10.1080/01411598408220327, 2-s2.0-0021375976.
10.1080/01411598408220327
CAS Google Scholar
6 Deorani S. C., Naithani U. C., and Semwal B. S., Four—spin contribution in DKDP, Indian Journal of Pure & Applied Physics. (1999) 37, 215–218.
CAS Web of Science® Google Scholar
7 Upadhyay T. C. and Semwal B. S., Temperature dependence of dielectric tangent loss in KDP and DKDP crystal at microwave frequencies, Indian Journal of Pure & Applied Physics. (2002) 40, 615–619.
CAS Web of Science® Google Scholar
8 Upadhyay T. C. and Semwal B. S., Microwave dielectric tangent losses in KDP and DKDP crystals, Pramana Journal of Physics. (2003) 60, no. 3, 525–533, https://doi.org/10.1007/bf02706161, 2-s2.0-0038343399.
10.1007/BF02706161
CAS Web of Science® Google Scholar
9 Upadhyay T. C., Bhandari R. S., and Semwal B. S., Dielectric properties of KDP-type ferroelectric crystals in the presence of external electric field, Pramana. (2006) 67, no. 3, 547–552, https://doi.org/10.1007/s12043-006-0016-y, 2-s2.0-33748807811.
10.1007/s12043-006-0016-y
CAS Web of Science® Google Scholar
10 Yurtseven H. and Şen S., Calculation of the spontaneous polarization and the dielectric constant as a function of temperature for KH₂PO₄, Advances in Condensed Matter Physics. (2012) 2012, 5, 259712, https://doi.org/10.1155/2012/259712, 2-s2.0-84867795199.
10.1155/2012/259712
Web of Science® Google Scholar
11 Kaminow I. P. and Damen T. C., Temperature dependence of the Ferroelectric mode in KH₂PO₄, Physical Review Letters. (1968) 20, no. 20, 1105–1108, https://doi.org/10.1103/physrevlett.20.1105, 2-s2.0-0000465821.
10.1103/PhysRevLett.20.1105
CAS Web of Science® Google Scholar
12 Lyddane R. H., Sachs R. G., and Teller E., On the polar vibrations of alkali halides, Physical Review. (1941) 59, no. 8, 673–676, https://doi.org/10.1103/PhysRev.59.673, ZBL0026.18004, 2-s2.0-36149010085.
10.1103/PhysRev.59.673
CAS Web of Science® Google Scholar
13 Scott J. F., Soft-mode spectroscopy: experimental studies of structural phase transitions, Reviews of Modern Physics. (1974) 46, no. 1, 83–128, https://doi.org/10.1103/revmodphys.46.83.
10.1103/RevModPhys.46.83
CAS Web of Science® Google Scholar
14 Blinc R., On the isotopic effects in the ferroelectric behaviour of crystals with short hydrogen bonds, Journal of Physics and Chemistry of Solids. (1960) 13, no. 3-4, 204–211, https://doi.org/10.1016/0022-3697(60)90003-2, 2-s2.0-34347381933.
10.1016/0022-3697(60)90003-2
CAS Web of Science® Google Scholar
15 Tokunaga M. and Matsubara T., Theory of ferroelectric phase transition in KH₂PO₄ type crystals I, Progress of Theoretical Physics. (1996) 35, 581–599.
10.1143/PTP.35.581
Google Scholar
16 de Gennes P. G., Collective motions of hydrogen bonds, Solid State Communications. (1963) 1, no. 6, 132–137, https://doi.org/10.1016/0038-1098(63)90212-6, 2-s2.0-2842572847.
10.1016/0038-1098(63)90212-6
CAS Web of Science® Google Scholar
17 Katiyar R. S., Ryan J. F., and Scott J. F., Proton-phonon coupling in CsH₂ AsO₄ and KH₂AsO₄, Physical Review B. (1971) 4, no. 8, 2635–2638, https://doi.org/10.1103/physrevb.4.2635, 2-s2.0-0000522942.
10.1103/PhysRevB.4.2635
Web of Science® Google Scholar
18 Labrenčič B., Levstek I., Žekš B., Blinc R., and Hadži D., Laser Raman study of quasi-spin wave hydrogen tunneling modes in KH₂PO₄ and KD₂PO₄, Chemical Physics Letters. (1970) 5, no. 7, 441–444, https://doi.org/10.1016/0009-2614(70)80057-4.
10.1016/0009-2614(70)80057-4
Web of Science® Google Scholar
19 Pak K. N., Strong coupling between proton and phonon in KDP, Physica Status Solidi B. (1973) 60, no. 1, 233–239, https://doi.org/10.1002/pssb.2220600125.
10.1002/pssb.2220600125
CAS Web of Science® Google Scholar
20 Deorani S. C., Singh P., and Yadav M. S., Investigation of deuteration effect on sound attenuation in hydrogen bonded ferroelectric crystals, Material Science Research India. (2011) 8, no. 1, 137–141.
10.13005/msri/080120
CAS Google Scholar
21 Panwar N. S. and Semwal B. S., Soft mode dynamics of ABO3—type trigonal ferroelectrics: application to lithium niobate, Indian Journal of Pure & Applied Physics (IJPAP). (1990) 28.
Google Scholar
22 Ramakrishnan V. and Tanaka T., Green′s-function theory of the ferroelectric phase transition in potassium dihydrogen phosphate (KDP), Physical Review B. (1977) 16, no. 1, 422–426, https://doi.org/10.1103/physrevb.16.422.
10.1103/PhysRevB.16.422
CAS Web of Science® Google Scholar
23 Ganguli S., Nath D., and Chaudhuri B. K., Green′s-function theory of phase transitions in hydrogen-bonded ferroelectric crystals with pseudo-spin-lattice coupled mode model, Physical Review B. (1980) 21, no. 7, 2937–2945, https://doi.org/10.1103/physrevb.21.2937, 2-s2.0-0011326031.
10.1103/PhysRevB.21.2937
CAS Web of Science® Google Scholar
24 Blinc R. and Žekš B., Proton order-disorder in KH₂PO₄-type ferroelectrics: slater theory and ising model in a transverse tunneling field, Ferroelectrics. (1987) 72, no. 1, 193–227, https://doi.org/10.1080/00150198708017947.
10.1080/00150198708017947
CAS Web of Science® Google Scholar
25 Zubarev D. N., Double-time green functions in statistical physics, Uspekhi Fizicheskikh Nauk. (1960) 71, 71–116, https://doi.org/10.3367/ufnr.0071.196005c.0071.
10.3367/UFNr.0071.196005c.0071
Web of Science® Google Scholar
26 Blinc R. and Zeks B., In soft modes in ferroelectrics and antiferroelectrics, Advance in Physics. (1972) 29.
Google Scholar
27 Zikai Q., Jinbo Z., and Chunlei W., Application of Green′s function method to the study of order-disorder ferroelectrics, Ferroelectrics. (1990) 101, no. 1, 159–169, https://doi.org/10.1080/00150199008016512.
10.1080/00150199008016512
Web of Science® Google Scholar
28 Kubo R., Statistical-mechanical theory of irreversible processes. I. general theory and simple applications to magnetic and conduction problems, Journal of the Physical Society of Japan. (1957) 12, no. 6, 570–586, https://doi.org/10.1143/jpsj.12.570, 2-s2.0-12344271673.
10.1143/JPSJ.12.570
Web of Science® Google Scholar
29 Litov E. and Garland C. W., Ultrasonic experiments in KDP-type crystals, Ferroelectrics. (1987) 72, no. 1, 19–44, https://doi.org/10.1080/00150198708017936.
10.1080/00150198708017936
CAS Web of Science® Google Scholar
30 Zurek R., Personal Communication, 1969.
Google Scholar
31 Pytte E., Soft-mode damping and ultrasonic attenuation at a structural phase transition, Physical Review B. (1970) 1, no. 2, 924–930, https://doi.org/10.1103/PhysRevB.1.924.
10.1103/PhysRevB.1.924
Web of Science® Google Scholar
32 Baumgartner H., Elektrische sättigungserscheinungen und elektrokalorischer effekt von kaliumphosphat KH2PO4, Helvetica Physica Acta. (1950) 24, no. 7.
Google Scholar
33 Choi B. and Lockwood D., Dielectric anomalies in KH₂PO₄, Ferroelectrics. (1990) 106, no. 1, 15–20, https://doi.org/10.1080/00150199008214552.
10.1080/00150199008214552
CAS Web of Science® Google Scholar
34 Takagi Y. and Shigenari T., Transverse susceptibility and E-mode Raman spectra of a KH₂PO₄ crystal, Journal of the Physical Society of Japan. (1975) 39, no. 2, 440–447, https://doi.org/10.1143/jpsj.39.440, 2-s2.0-33847339337.
10.1143/JPSJ.39.440
CAS Web of Science® Google Scholar
35 Kaminow I. P. and Harding G. O., Complex dielectric constant of KH₂PO₄ at 9.2 Gc/sec, Physical Review. (1963) 129, no. 4, 1562–1566, https://doi.org/10.1103/physrev.129.1562, 2-s2.0-0013155933.
10.1103/PhysRev.129.1562
CAS Web of Science® Google Scholar
36 Havlin S., Litov E., and Uehling E. A., Transverse susceptibility in KH₂PO₄-type crystals, Physical Review B. (1974) 9, no. 3, article 1024, https://doi.org/10.1103/physrevb.9.1024, 2-s2.0-0007176582.
10.1103/PhysRevB.9.1024
Web of Science® Google Scholar
37 Deguchi K. and Nakamura E., Deviation from the Curie-Weiss Law in KH₂PO₄, Journal of the Physical Society of Japan. (1980) 49, no. 5, 1887–1891, https://doi.org/10.1143/jpsj.49.1887, 2-s2.0-0019087189.
10.1143/JPSJ.49.1887
CAS Web of Science® Google Scholar
38 Hill R. M. and Ichiki S. K., High-frequency behavior of hydrogen-bonded ferroelectrics: triglycine sulphate and KD₂PO₄, Physical Review. (1963) 132, no. 4, 1603–1608, https://doi.org/10.1103/physrev.132.1603, 2-s2.0-33746755669.
10.1103/PhysRev.132.1603
CAS Web of Science® Google Scholar
39 Mason W. P., Theory of the ferroelectric effect and clamped dielectric constant of Rochelle salt, Physical Review. (1947) 72, no. 9, 854–865, https://doi.org/10.1103/physrev.72.854, 2-s2.0-0037760564.
10.1103/PhysRev.72.854
CAS Web of Science® Google Scholar
40 Konwent H., On the theory of hydrogen-bonded ferroelectrics, Physica Status Solidi B. (1968) 28, no. 1, 39–44, https://doi.org/10.1002/pssb.19680280103.
10.1002/pssb.19680280103
CAS Web of Science® Google Scholar

All articles

Study of Dielectric Properties and Ultrasonic Attenuation in KDP-Type Ferroelectrics

Abstract

1. Introduction

2. The Model Hamiltonian and Green’s Function

2.1. Collective Proton Wave Width and Shift