Efforts have been made to present a comparison of all the three magnetic fluid flow models (Neuringer-Rosensweig model, Shliomis model, and Jenkins model) so far as the performance of a magnetic fluid based parallel plate rough slider bearing is concerned. The stochastic model of Christensen and Tonder is adopted for the evaluation of effect of transverse surface roughness. The stochastically averaged Reynolds-type equation is solved with suitable boundary conditions to obtain the pressure distribution resulting in the calculation of load carrying capacity. The graphical results establish that for a bearing’s long life period the Shliomis model may be employed for higher loads. However, for lower to moderate loads, the Neuringer-Rosensweig model may be deployed.

1. Introduction

The analysis of hydrodynamic lubrication of a nonporous slider bearing is a classical one. The exact solution of Reynolds equation for slider bearings with different simple film geometries is discussed in a number of research papers and books [1–4]. The squeeze film slider bearing is used in clutch plates, automobile transmissions, and domestic appliances. Due to this, many investigators [4–8] dealt with the problem of squeeze film slider bearing.

During the last few years a noticeable amount of interest in tribology research has been devoted to the study of effect of surface roughness on the hydrodynamic lubrication because most of the bearing surfaces become rough after having some run-in and wear.

Bearing surface could be roughened through the manufacturing process, the wear, and the impulsive damage. Surface roughness evaluation is very essential for many fundamental problems such as contact deformation, friction, heat and electric current conduction, tightness of contact joints, and positional accuracy. To study the effect of surface roughness, Christensen and Tonder [9–11] utilized a stochastic concept and developed an averaging film model to lubricated surfaces with transverse roughness. On the basis of Christensen and Tonder’s stochastic model of roughness, Ting [12] presented a simple mathematical analog for determination of the squeeze film behavior between two parallel annular disks. Prakash and Tiwari [13] analyzed the effect of surface roughness on the response of a squeeze film between two circular plates when one plate had a porous facing. Guha [14] investigated the concept of a stochastic process which was applied to the problem of surface roughness in the dynamic characteristics of hydrodynamic journal bearings of finite width. Turaga et al. [15] studied a Reynolds-type equation for finite hydrodynamic bearings (plane slider and cylindrical journal) with rough surfaces (longitudinal, transverse, and isotropic roughness). Gururajan and Prakash [16] examined the effect of surface roughness in hydrodynamic narrow porous journal hearings operating under steady conditions. It was shown that the results were significantly different than those for the case of an infinitely long journal bearing. Gadelmawla et al. [17] proposed the mathematical formulation of surface roughness parameter. Sinha and Adamu [18] discussed the thermal and roughness effects on the performance characteristics of an infinite tilted pad slider bearing. It was observed that, for a nonparallel slider bearing, the load carrying capacity due to the combined effect was less than the load capacity due to the roughness effect for both models. Adamu and Sinha [19] analyzed the thermal and roughness effects on different characteristics of an infinitely long tilted pad slider bearing considering heat conduction through both the pad and the slider.

In fact, ferrofluid can solve many difficult sealing, lubricating, detection, heat transfer, and damping problems. Ferrofluid based devices have found applications in high-vacuum equipment, laser systems, computers, inertia dampers, loudspeakers, material separation, domain detection, and many other areas. Among the many applications in engineering are those taking advantage of the possibility of collecting and holding firmly small quantities of such fluids in a region with highly focused magnetic fields.

Neuringer and Rosensweig [20] developed a simple flow model to describe the steady flow of magnetic fluids in the presence of slowly changing external magnetic fields. A good number of papers are available in the literature for the study of different types of bearing using Neuringer and Rosensweig flow model, for example, Tipei [21] in short bearing, Agrawal [22], Shah and Bhat [23], and Deheri and Patel [4] in slider bearing, journal bearing by Nada and Osman [24] and Patel et al. [25], and circular plates by Shah and Bhat [26] and Deheri and Abhangi [27]. Later on, the flow model of Neuringer and Rosensweig was modified by Jenkins [28] with Maugin’s modification. It was found that Neuringer-Rosensweig model modified pressure while Jenkins flow model modified both the pressure and the velocity of the ferrofluid. The steady-state performance of bearings with Jenkins model based magnetic fluids was discussed by Agrawal [22], Ram and Verma [29], and Shah and Bhat [30]. Ahmad and Singh [31] analyzed the theoretical model of a magnetic fluid lubrication of porous-pivoted slider bearing with slip velocity. Patel and Deheri [32, 33] dealt with the effect of slip velocity and surface roughness on the performance of Jenkins model based magnetic squeeze film in curved rough circular plates. It was manifested that for any type of improvement in the performance characteristics the slip parameter was required to be reduced even if variance (−ve) occurred and suitable magnetic strength was in force. Also, all the above studies established that the load carrying capacity of the bearing system increased with increasing magnetization. Patel and Deheri [34] investigated the combined effect of slip velocity and surface roughness on the performance of Jenkins model based magnetic squeeze film in curved rough annular plates. It was observed that the effect of transverse surface roughness remained adverse in general; Jenkins model based ferrofluid lubrication provided some measures in mitigating the adverse effect and this became more manifest when the slip parameter was reduced and negatively skewed roughness occurred.

In the last few years, the fact that the magnetic fluid when used as a lubricant turns in an enhanced performance has drawn significant attentions all over the world. On the other hand Shliomis [35] proposed a ferrofluid flow model, in which the effects of rotation of magnetic particles, their magnetic moments, and the volume concentration were included. Kumar et al. [36] analyzed the effect of a ferrofluid squeeze film for spherical and conical bearings with a constant external magnetic field applied in the direction transverse to that of fluid flow. Singh and Gupta [37] theoretically discussed the effect of ferrofluid on the dynamic characteristics of curved slider bearings using Shliomis model. On the ground of the ferrohydrodynamic model proposed by Shliomis [35], Lin [38] discussed the influence of fluid inertia forces on the ferrofluid squeeze film between a sphere and a plate in the presence of external magnetic fields. It was observed from the above studies that the volume concentration and the intensity of magnetic field provided an increase in the load carrying capacity and the time of approach. All these researchers have found the steady-state characteristics of the bearings lubricated with magnetic fluids, resorting to the model proposed by Shliomis [35]. Patel and Deheri [32, 33] discussed the effect of different porous structures on the performance of a Shliomis model based magnetic squeeze film in rotating rough porous curved circular plates. It was shown that the adverse effect of transverse roughness could be compensated by the positive effect of magnetization in the case of negatively skewed roughness, suitably choosing the rotation ratio and the curvature parameters.

Till today there is no investigation regarding the comparison of the three well-known magnetic fluid flow models, so far as bearing performance is concerned. So it was deemed appropriate to launch an investigation into the performance of a ferrofluid based rough parallel plate slider bearing, considering all the three ferrofluid flow models. This adds a new dimension as the roughness also is factored into the discussion.

In fact, the aim of the current study is to analyze the effect of a ferrofluid based rough parallel plate slider bearing considering the comparison of three magnetic fluid flow models, namely, Neuringer-Rosensweig model, Shliomis model, and Jenkins model.

2. Analysis

The physical configuration of the parallel plate slider bearing is presented in Figure 1. The slider moves with a uniform velocity U in the x direction and squeeze velocity in the z direction, h₀ being the minimum film thickness. The length is A and B is the breadth of the bearing in the y direction.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Configuration of the bearing system.

The bearing surfaces are considered to be transversely rough. In view of the discussions of Christensen and Tonder [9–11], the thickness h of the lubricant film is taken as

()

where

denotes the mean film thickness and h_s is the deviation from the mean film thickness characterizing the random roughness of the bearing surfaces. h_s is assumed to be stochastic in nature and governed by the probability density function

()

where c is the maximum deviation from the mean film thickness. The mean α, the standard deviation σ, and the parameter ε, which is the measure of symmetry of the random variable h_s, are defined by the relations

()

where E denotes the expected value given by

()

The details can be seen from Christensen and Tonder [9–11].

The lubricant film is assumed to be isoviscous and incompressible and the flow is laminar. A magnetic fluid is used as the lubricant in present study. The magnetic field is oblique to the lower plate as considered in Agrawal [22]. Prajapati [39] discussed the effect of various forms of the magnitude of the magnetic field on the squeeze film performance. Following Prajapati [39] and Bhat [40] the magnitude of the magnetic field is considered as

()

where K is suitably chosen to suit the dimensions of both sides and strength of the magnetic field, the details of which can be found in Bhat and Deheri [7] and Patel and Deheri [41].

In 1964, Neuringer and Rosensweig developed a simple model to describe the steady flow of magnetic fluids in the presence of slowly changing external magnetic fields. The model consists of the following equations:

()

where ρ is the fluid density,

represents the fluid velocity in the film region,

denotes the external magnetic field,

is the magnetic susceptibility of the magnetic field, p represents the film pressure, η denotes the fluid viscosity, and μ₀ is the permeability of the free space. The details of all these parameters have been treated in Bhat [40] and Prajapati [39].

Using (8)-(9), (6) becomes

()

Therefore, the modified Reynolds equation for parallel plate slider bearing for Neuringer and Rosensweig model is obtained as

()

Shliomis [35] pointed out that magnetic particles of a magnetic fluid could relax in two ways when the applied magnetic field changed. One was by the rotation of magnetic particles in the fluid and the other one by rotation of the magnetic moment within the particles. The particle rotation is given by Brownian relaxation time parameters τ_B while the intrinsic rotational process is described by the relaxation time parameters τ_S. Assuming steady flow and neglecting inertial and second derivatives of

, the equations governing the flow become

()

where

is the internal angular momentum and I is the sum of moments of inertia of the particles per unit volume:

()

together with

()

As discussed in [40],

is the fluid viscosity in the film region,

is external magnetic field,

is magnetic susceptibility of the magnetic field, p is the film pressure, η is the fluid viscosity, and μ₀ is the permeability of the free space.

By making use of (14) in (13) and (15), one finds that

()

Neglecting τ_B τ_S terms, substitution of

in the above equation leads to

()

From (19), it is easily observed that an initial approximation to

()

Substituting the value of

on the right side of (19), a second approximation to

is found to be

()

Again, substituting this value of

on the right side of (19), a third approximation to

is availed as

()

Making use of this model, Bhat [40] and Patel and Deheri [32, 33], the modified Reynolds-type equation for Shliomis model for a one-dimensional flow as in a slider bearing with the slider moving with a uniform velocity U in the x direction and for impermeable slider bearing the governing equation is

()

The details are explained in Bhat [40].

In [28], Jenkins proposed a model to describe the flow of a ferrofluid. In view of Maugin’s modification, equations of the model for steady flow are [28, 29]

()

together with (7)–(10), where J is a material constant. From (6) and (25) it is observed that Jenkins model is a generalization of Neuringer-Rosensweig model with an additional term

()

which modifies the velocity of the fluid.

In view of Bhat [40] and Patel and Deheri [32, 33], the modified Reynolds equation for Jenkins model of a one-dimensional flow, in Cartesian coordinates, turns out to be

()

Under the usual assumptions of hydrodynamic lubrication [8, 39, 40] and the stochastic modelling of Christensen and Tonder [9–11] the modified Reynolds’ equation governing the pressure distribution takes the form for Neuringer-Rosensweig model, Shliomis model, and Jenkins model, respectively, as

()

where

()

The concerned boundary conditions are

()

Introducing the nondimensional quantities,

()

and for Shliomis model

()

and using (25), (19)–(23) reduce to

()

where

()

Solving (35) under the boundary conditions (32), one can find the dimensionless pressure for Neuringer-Rosensweig model, Shliomis model, and Jenkins model, respectively:

()

The dimensionless load carrying capacity takes the form for all three cases, respectively, as

()

3. Results and Discussions

It is noticed that the nondimensional pressure distribution is given by (37)–(39) while (40)–(42) determine the nondimensional load carrying capacity. It is well known that the magnetization increases the viscosity of the lubricant which results in increased pressure and, consequently, the load carrying capacity. As (40)–(42) are linear with respect to magnetization parameter, an increase in the magnetization would lead to increased load carrying capacity.

The effect of magnetization parameter on the load carrying capacity is displayed in Table 1 and Figures 2-5–6. It is seen that the magnetization parameter causes increased load carrying capacity.

Table 1. Variation of load carrying capacity with respect to μ^∗/τ and

μ^∗/τ→	0.1	0.2	0.3	0.4	0.5
NR	1.246478	1.254811	1.263145	1.271478	1.279811	0.01
Sh	1.078984	1.177073	1.275163	1.373252	1.471342
Je	1.242833	1.251167	1.2595	1.267833	1.276167

NR	1.245169	1.253502	1.261835	1.270169	1.278502	0.02
Sh	1.078539	1.176587	1.274636	1.372685	1.470734
Je	1.241528	1.249861	1.258194	1.266528	1.274861

NR	1.242993	1.251326	1.259659	1.267993	1.276326	0.03
Sh	1.077797	1.175779	1.273761	1.371742	1.469724
Je	1.239358	1.247691	1.256025	1.264358	1.272691

NR	1.239959	1.248292	1.256626	1.264959	1.273292	0.04
Sh	1.076763	1.17465	1.272538	1.370425	1.468313
Je	1.236333	1.244667	1.253	1.261333	1.269667

NR	1.23608	1.244414	1.252747	1.26108	1.269414	0.05
Sh	1.075437	1.173204	1.270971	1.368738	1.466506
Je	1.232466	1.2408	1.249133	1.257466	1.2658

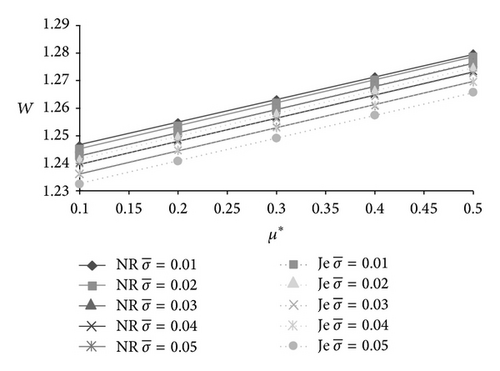
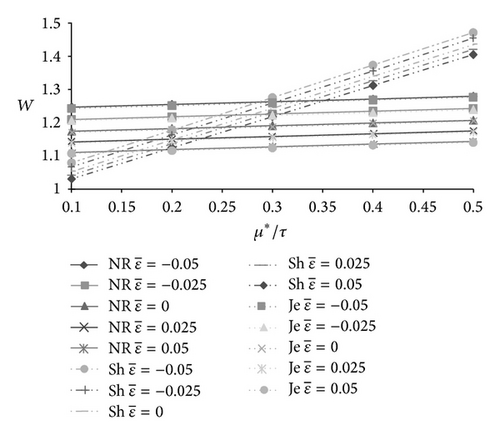
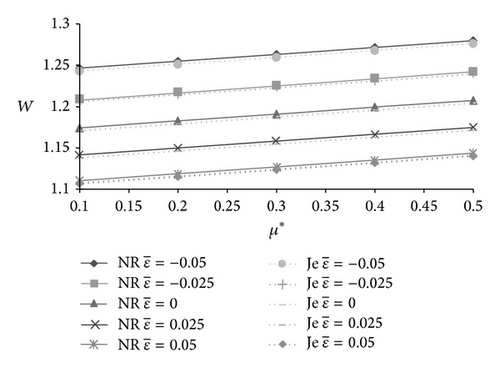
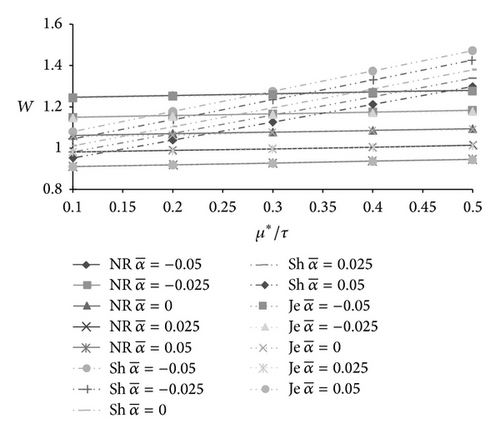
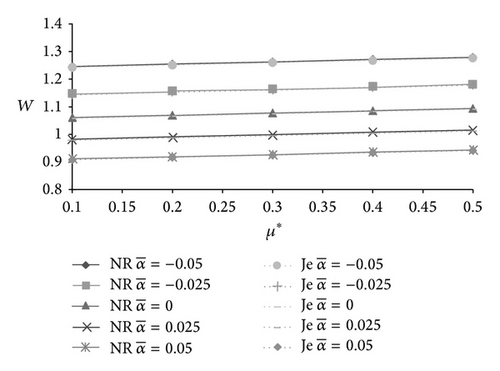
The following short version has been taken for the three models: NR stands for Neuringer-Rosensweig model, Sh stands for Shliomis model, and the symbol for Jenkins model is Je.

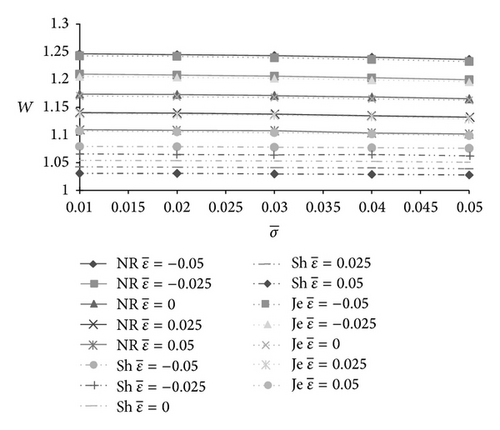
The influence of standard deviation on load carrying capacity is presented in Figures 7-9–10. As such, the transverse surface roughness affects the bearing performance adversely. Probably this may be due to the reason that the motion of the lubricant gets retarded by roughness. However, the standard deviation fails to reduce the load significantly.

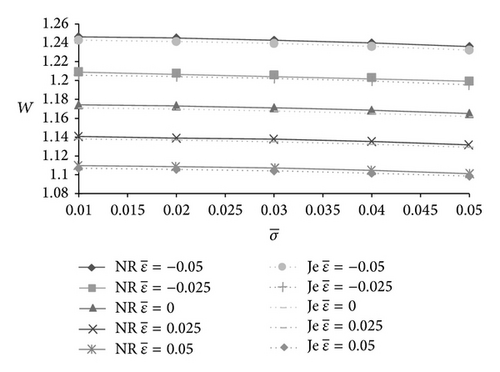
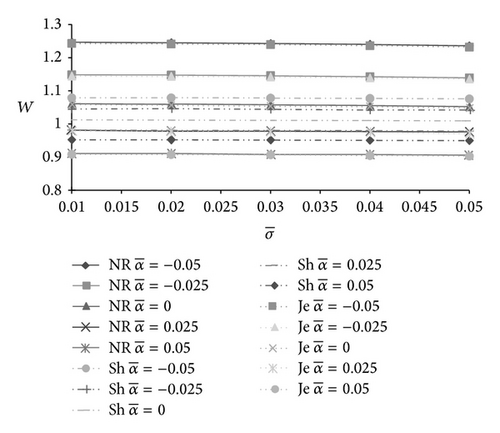
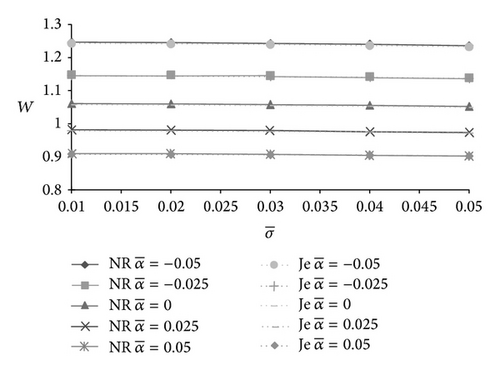
In Figures 11-12, the effect of skewness on load carrying capacity is presented. The positively skewed roughness decreases the load carrying capacity while the nondimensional load increases due to the negatively skewed roughness. It is interesting to note that variance also follows the path of skewness so far as the trends of load carrying capacity are concerned. Thus, the negatively skewed roughness-variance (−ve) combination induces a positive effect.

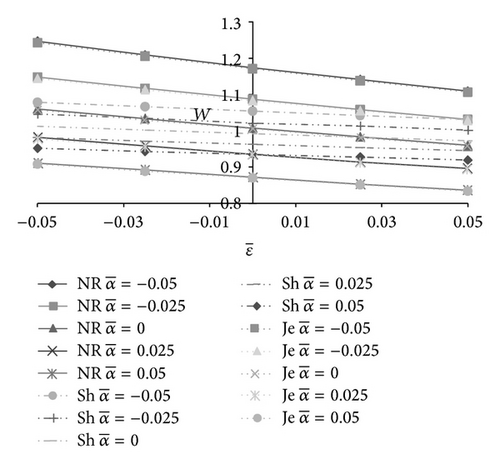
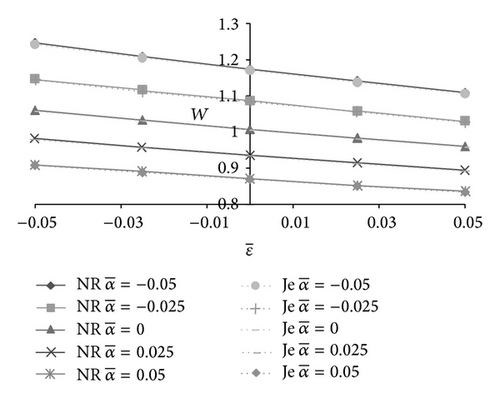
In order to boost the bearing performance this paper suggests that the combined positive effect of negatively skewed roughness and variance (−ve) may be channelized for bearing design.

A comparison has been given below regarding the performance characteristics of a magnetic fluid based parallel plate slider bearing. The three models, namely, Neuringer-Rosensweig model, Shliomis model, and Jenkins model, of magnetic fluid flow are considered for the comparison. A comparison of the graphical representation yields the following:

(1)
The magnetic fluid lubrication improves the bearing performance in case of all the three models because the magnetization induces an increase in the viscosity of the lubricant.
(2)
However, the Shliomis model remains more effective as compared to the other two models so far as the effect of skewness is concerned. Further, the Neuringer-Rosensweig model and Jenkins model provide the same type of trends when skewness is taken into account.
(3)
With respect to the effect of variance on the bearing performance once again the Shliomis model goes ahead of the other two models.
(4)
Up to some extent the effect of standard deviation remains predominant in Shliomis model as compared to the other two models.
(5)
In comparison with the other two models, the standard deviation causes severe load reduction in Jenkins model.
(6)
The effect of negatively skewed roughness (which increases the load carrying capacity) remains more effective in Neuringer-Rosensweig model. The same is the case with respect to variance (−ve).

A close observation of the analysis presented here indicates that the load carrying capacity is enhanced by at least 7-8% as compared to the conventional fluid based rough slider bearing system.

4. Conclusion

This paper confirms that when the bearing has run for a longer time, the Neuringer-Rosensweig model may be preferred in order to counter the effect of roughness. However, the Shliomis model may be considered for higher loads, as compared to the other two models for this type of bearing system. The effects of Neuringer-Rosensweig model and Jenkins model are almost alike for nominal roughness. In addition, this type of bearing system supports a good amount of load even in the absence of flow, unlike the case of a traditional lubricant based bearing system. This investigation strongly indicates that the roughness aspect must be considered while designing the bearing system even if Shliomis model is in place.

Competing Interests

The authors declare that they have no competing interests.

References

1 Cameron A., Principles of Lubrication, 1966, Longmans, London, UK.
Google Scholar
2 Basu S. K., Sengupta S. N., and Ahuja B. B., Fundamentals of Tribology, 2005, Prentice-Hall, New Delhi, India.
Google Scholar
3 Majumdar B. C., Introduction to Tribology of Bearings, 2008, S. Chand and Company Limited, New Delhi, India.
Google Scholar
4 Deheri G. M. and Patel J. R., Magnetic fluid based squeeze film in a rough porous parallel plate slider bearing, Annals of Faculty Engineering Hunedoara: International Journal of Engineering. (2011) 9, no. 3, 443–448.
Google Scholar
5 Prakash J. and Vij S. K., Hydrodynamic lubrication of porous slider, Journal of Mechanical Engineering Science. (1973) 15, no. 3, 232–234, https://doi.org/10.1243/jmes_jour_1973_015_039_02, 2-s2.0-0015636444.
10.1243/JMES_JOUR_1973_015_039_02
Google Scholar
6 Bhat M. V., Hydrodynamic lubrication of porous composite slider bearings, Japanese Journal of Applied Physics. (1978) 17, no. 3.
10.1143/JJAP.17.479
Web of Science® Google Scholar
7 Bhat M. V. and Deheri G. M., Porous slider bearing with squeeze film formed by a magnetic fluid, Pure and Applied Mathematika Sciences. (1995) 39, no. 1-2, 39–43.
Google Scholar
8 Deheri G. M., Andharia P. I., and Patel R. M., Transversely rough slider bearings with squeeze film formed by a magnetic fluid, International Journal of Applied Mechanics and Engineering. (2005) 10, no. 1, 53–76, Zbl1195.76427.
Google Scholar
9 Christensen H. and Tonder K. C., Tribology of rough surfaces: stochastic models of hydrodynamic lubrication, 1969, no. 10/69-18, SINTEF.
Google Scholar
10 Christensen H. and Tonder K. C., Tribology of rough surfaces: parametric study and comparison of lubrication models, SINTEF, Report, 1969, no. 22/69-18.
Google Scholar
11 Christensen H. and Tonder K., The hydrodynamic lubrication of rough bearing surfaces of finite width, Journal of Lubrication Technology. (1971) 93, no. 3, 324–329, https://doi.org/10.1115/1.3451579.
10.1115/1.3451579
Google Scholar
12 Ting L. L., A Mathematical analog for determination of porous annular disk squeeze film behavior including the fluid inertia effect, Transactions of the ASME. Journal of Basic Engineering. (1972) 94, no. 2, 417–421, https://doi.org/10.1115/1.3425437, 2-s2.0-0015360294.
10.1115/1.3425437
Google Scholar
13 Prakash J. and Tiwari K., Roughness effects in porous circular squeeze-plates with arbitrary wall thickness, Journal of Lubrication Technology. (1983) 105, no. 1, 90–95, https://doi.org/10.1115/1.3254554, 2-s2.0-0020548481.
10.1115/1.3254554
Google Scholar
14 Guha S. K., Analysis of dynamic characteristics of hydrodynamic journal bearings with isotropic roughness effects, Wear. (1993) 167, no. 2, 173–179, https://doi.org/10.1016/0043-1648(93)90322-D, 2-s2.0-0027906196.
10.1016/0043-1648(93)90322-D
Web of Science® Google Scholar
15 Turaga R., Sekhar A. S., and Majumdar B. C., Stochastic FEM analysis of finite hydrodynamic bearings with rough surfaces, Tribology Transactions. (1997) 40, no. 4, 605–612, https://doi.org/10.1080/10402009708983698, 2-s2.0-0031253552.
10.1080/10402009708983698
CAS Web of Science® Google Scholar
16 Gururajan K. and Prakash J., Effect of surface roughness in a narrow porous journal bearing, Journal of Tribology. (2000) 122, no. 2, 472–475, https://doi.org/10.1115/1.555387, 2-s2.0-0034174265.
10.1115/1.555387
Web of Science® Google Scholar
17 Gadelmawla E. S., Koura M. M., Maksoud T. M. A., Elewa I. M., and Soliman H. H., Roughness parameters, Journal of Materials Processing Technology. (2002) 123, no. 1, 133–145, https://doi.org/10.1016/s0924-0136(02)00060-2, 2-s2.0-0037051748.
10.1016/S0924-0136(02)00060-2
Web of Science® Google Scholar
18 Sinha P. and Adamu G., THD analysis for slider bearing with roughness: special reference to load generation in parallel sliders, Acta Mechanica. (2009) 207, no. 1-2, 11–27, https://doi.org/10.1007/s00707-008-0094-7, 2-s2.0-68849098582.
10.1007/s00707-008-0094-7
Web of Science® Google Scholar
19 Adamu G. and Sinha P., Thermal and roughness effects in a tilted pad slider bearing considering heat conduction through the pad and slider, Proceedings of the National Academy of Sciences A: Physical Sciences. (2012) 82, no. 4, 323–333, https://doi.org/10.1007/s40010-012-0046-4, MR3019998.
10.1007/s40010-012-0046-4
Web of Science® Google Scholar
20 Neuringer J. L. and Rosensweig R. E., Magnetic fluids, The Physics of Fluids. (1964) 7, no. 12, 1927–1937, https://doi.org/10.1063/1.1711103, MR0178690.
10.1063/1.1711103
Web of Science® Google Scholar
21 Tipei N., Theory of lubrication with ferrofluids: application to short bearings, Journal of Lubrication Technology. (1982) 104, no. 4, 510–515, https://doi.org/10.1115/1.3253274, 2-s2.0-0019922583.
10.1115/1.3253274
Web of Science® Google Scholar
22 Agrawal V. K., Magnetic-fluid-based porous inclined slider bearing, Wear. (1986) 107, no. 2, 133–139, https://doi.org/10.1016/0043-1648(86)90023-2, 2-s2.0-0022557910.
10.1016/0043-1648(86)90023-2
Web of Science® Google Scholar
23 Shah R. C. and Bhat M. V., Magnetic fluid based porous inclined slider bearing with velocity slip, International Journal of Applied Mechanics and Engineering. (2003) 18, no. 2, 331–336, Zbl1145.76447.
Google Scholar
24 Nada G. S. and Osman T. A., Static performance of finite hydrodynamic journal bearings lubricated by magnetic fluids with couple stresses, Tribology Letters. (2007) 27, no. 3, 261–268, https://doi.org/10.1007/s11249-007-9222-0, 2-s2.0-34547141105.
10.1007/s11249-007-9222-0
Web of Science® Google Scholar
25 Patel N. S., Vakharia D. P., and Deheri G. M., A study on the performance of a magnetic-fluid-based hydrodynamic short journal bearing, ISRN Mechanical Engineering. (2012) 2012, 7, 603460, https://doi.org/10.5402/2012/603460.
10.5402/2012/603460
Google Scholar
26 Shah R. C. and Bhat M. V., Squeeze film based on magnetic fluid in curved porous rotating circular plates, Journal of Magnetism and Magnetic Materials. (2000) 208, no. 1, 115–119, https://doi.org/10.1016/s0304-8853(99)00570-3, 2-s2.0-0033889010.
10.1016/S0304-8853(99)00570-3
CAS Web of Science® Google Scholar
27 Deheri G. M. and Abhangi N. D., Numerical modelling of a magnetic fluid-based squeeze film between rotating transversely rough curved circular plates, International Journal of Computational Materials Science and Surface Engineering. (2011) 4, no. 3, 185–204, https://doi.org/10.1504/ijcmsse.2011.042825, 2-s2.0-80053635685.
10.1504/IJCMSSE.2011.042825
Google Scholar
28 Jenkins J. T., A theory of magnetic fluids, Archive for Rational Mechanics and Analysis. (1972) 46, 42–60, https://doi.org/10.1007/BF00251867, MR0334688, ZBL0241.76014, 2-s2.0-0040212448.
10.1007/BF00251867
Web of Science® Google Scholar
29 Ram P. and Verma P. D. S., Ferrofluid lubrication in porous inclined slider bearing, Indian Journal of Pure and Applied Mathematics. (1999) 30, no. 12, 1273–1281, ZBL0947.76098, 2-s2.0-0033263983.
Web of Science® Google Scholar
30 Shah R. C. and Bhat M. V., Ferrofluid lubrication in porous inclined slider bearing with velocity slip, International Journal of Mechanical Sciences. (2002) 44, no. 12, 2495–2502, https://doi.org/10.1016/S0020-7403(02)00187-X, ZBL1026.76511, 2-s2.0-0036995972.
10.1016/S0020-7403(02)00187-X
Web of Science® Google Scholar
31 Ahmad N. and Singh J. P., Magnetic fluid lubrication of porous pivoted slider bearing with slip velocity, Proceedings of the Institution of Mechanical Engineers Part J: Journal of Engineering Tribology. (2007) 221, no. 5, 609–613, https://doi.org/10.1243/13506501jet272, 2-s2.0-34848825666.
10.1243/13506501JET272
Web of Science® Google Scholar
32 Patel J. R. and Deheri G., Combined effect of surface roughness and slip velocity on jenkins model based magnetic squeeze film in curved rough circular plates, International Journal of Computational Mathematics. (2014) 2014, 9, 367618, https://doi.org/10.1155/2014/367618.
10.1155/2014/367618
Google Scholar
33 Patel J. R. and Deheri G., Shliomis model-based magnetic squeeze film in rotating rough curved circular plates: a comparison of two different porous structures, International Journal of Computational Materials Science and Surface Engineering. (2014) 6, no. 1, 29–49, https://doi.org/10.1504/ijcmsse.2014.063760, 2-s2.0-84904720169.
10.1504/IJCMSSE.2014.063760
Google Scholar
34 Patel J. R. and Deheri G. M., Jenkins model based ferrofluid lubrication of a curved rough annular squeeze film with slip velocity, Tribology in Industry. (2015) 37, no. 2, 129–141, 2-s2.0-84934760294.
Google Scholar
35 Shliomis M. I., Effective viscosity of magnetic suspensions, Soviet Physics—Journal of Experimental and Theoretical Physics. (1972) 34, no. 6, 1291–1294.
Web of Science® Google Scholar
36 Kumar D., Sinha P., and Chandra P., Ferrofluid squeeze film for spherical and conical bearings, International Journal of Engineering Science. (1992) 30, no. 5, 645–656, https://doi.org/10.1016/0020-7225(92)90008-5, ZBL0756.76085, 2-s2.0-0026868007.
10.1016/0020-7225(92)90008-5
CAS Web of Science® Google Scholar
37 Singh U. P. and Gupta R. S., Dynamic performance characteristics of a curved slider bearing operating with ferrofluids, Advances in Tribology. (2012) 2012, 6, 278723, https://doi.org/10.1155/2012/278723, 2-s2.0-84866245249.
10.1155/2012/278723
Google Scholar
38 Lin J.-R., Fluid inertia effects in ferrofluid squeeze film between a sphere and a plate, Applied Mathematical Modelling. (2013) 37, no. 7, 5528–5535, https://doi.org/10.1016/j.apm.2012.09.030, MR3020669, 2-s2.0-84872611387.
10.1016/j.apm.2012.09.030
Web of Science® Google Scholar
39 Prajapati B. L., On certain theoretical studies in hydrodynamic and electro-magneto hydrodynamic lubrication [Ph.D. thesis], 1995, S.P. University, Vallabh Vidhyanagar, Undia.
Google Scholar
40 Bhat M. V., Lubrication with a Magnetic Fluid, 2003, Team Spirit India, Ahmedabad, India.
Google Scholar
41 Patel J. R. and Deheri G. M., A comparison of porous structures on the performance of a magnetic fluid based rough short bearing, Tribology in Industry. (2013) 35, no. 3, 177–189, 2-s2.0-84884542762.
Google Scholar

Citing Literature

All articles

Performance of a Ferrofluid Based Rough Parallel Plate Slider Bearing: A Comparison of Three Magnetic Fluid Flow Models

Abstract

1. Introduction

2. Analysis

3. Results and Discussions

4. Conclusion

Competing Interests

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Performance of a Ferrofluid Based Rough Parallel Plate Slider Bearing: A Comparison of Three Magnetic Fluid Flow Models

Abstract

1. Introduction

2. Analysis

3. Results and Discussions

4. Conclusion

Competing Interests

References

Citing Literature

Figures

References

Related

Information