In recent years a multitude of events have created a new environment for the electric power infrastructure. The presence of small-scale generation near load spots is becoming common especially with the advent of renewable energy sources such as wind power energy. This type of generation is known as distributed generation (DG). The expansion of the distributed generators- (DGs-) based wind energy raises constraints on the distribution networks operation and power quality issues: voltage sag, voltage swell, voltage interruption, harmonic contents, flickering, frequency deviation, unbalance, and so forth. Consequently, the public distribution network conception and connection studies evolve in order to keep the distribution system operating in optimal conditions. In this paper, a comprehensive power quality investigation of a distribution system with embedded wind turbines has been carried out. This investigation is carried out in a comparison aspect between the conventional synchronous generators, as DGs are widely in use at present, and the different wind turbines technologies, which represent the foresightedness of the DGs. The obtained results are discussed with the IEC 61400-21 standard for testing and assessing power quality characteristics of grid-connected wind energy and the IEEE 1547-2003 standard for interconnecting distributed resources with electric power systems.

1. Introduction

Nowadays, power quality (PQ) in the distribution systems has been a research area of exponentially increasing interest because of an increasing concern to both distribution utilities and customers. The increased concern of power quality has resulted in measuring power quality variations and characteristic disturbances for different customer categories. Load switching, system faults, motor starting, load variations, nonlinear loads, intermittent loads, and arc furnaces usually cause power quality disturbances. These cause many electrical disturbances such as voltage sag, swell, harmonic distortions, interruptions, flicker, and unbalance. Power quality assessment is very important for operation of devices in customer side and its issue is also important for the utility companies that are obliged to supply consumers with electrical power of acceptable quality [1–5].

Wind power turbines have, nowadays, increasing penetration levels in power grids for their splendid reserve. The wind turbine can be connected to either a high voltage network, as a wind farm, or distribution systems, as individual turbines. Such power turbines have their own characteristics and operation modes. Consequently, several challenges arise concerning their impacts on the power system profile regarding the power quality issues [6, 7].

Considering the frequent occurrence of power quality problems in the distribution system, in addition to the new trend for using wind turbines as new distributed generators (DGs), the power quality analysis of the distribution system considering different technologies of wind turbines becomes imperatively important. Therefore, in this paper, a comprehensive study of the power quality problems for a considered 15-bus radial distribution system with embedded distributed generators (DGs) has been carried out. Different technologies of the DGs have been considered. The power quality studies are carried out in a comparison aspect between the conventional synchronous generator, as DGs are widely in use at present, and the different wind turbines technologies, which represent the foresightedness of the DGs. The absence of DGs is assumed as a base case for the studies.

This paper is organized as follows. Section 2 describes the considered distribution system component modelling. The steady state voltage profile of the considered system is given in Section 3. Section 4 presents a complete study about voltage sag, voltage swell, and voltage interruption during load variation and system disturbances. Voltage fluctuation and flicker resulting from wind speed variation and pulsating loads are analyzed in Section 5. The harmonic distortion supplied by the wind turbine generators and the nonlinear loads are investigated in Section 6. Section 7 discusses the electrical power losses and the effect of wind turbine output power and connection point on power loss values. Finally, Section 8 summarizes the main conclusions.

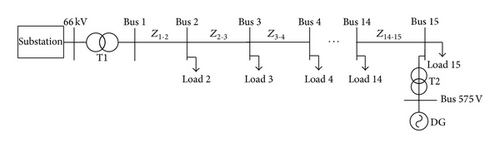
2. Configuration of the Considered Distribution System

In this paper, the 15-bus radial distribution system, shown in Figure 1, is considered. All the system data are given in the Appendix. Each of the feeder sections is represented by series RL impedance and the system transformers are modelled by its T-equivalent circuit. In the steady state studies, the loads are represented by constant power models, as is usual in the load flow studies, while in the dynamic studies the loads are represented by constant impedance. The simulation package adopted is the Sim-Power Systems for use with Matlab/Simulink.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Single line diagram of the considered 15-bus distribution system.

The DGs considered in this paper are the conventional synchronous generators, which are widely in use at present, in addition to the wind turbine generators, which represent the foresightedness of the DGs. The wind turbines generators can be classified as fixed speed and variable speed wind turbines generators. The fixed speed induction generator (FSIG) wind turbine is equipped with a squirrel-cage induction generator while the variable speed wind turbines can be either a partially rated converter- or a fully rated converter-based wind turbine. The partially rated converter-based wind turbines are always equipped with a double fed induction generator (DFIG). The fully rated converter-based wind turbine can be equipped with a wound rotor induction generator or a conventional synchronous generator or a permanent magnet synchronous generator (PMSG). The PMSG is the one commonly used for avoiding the field current supply, needed by wound rotor synchronous generators, or because of the reactive power compensation facilities, needed by induction generators. Furthermore, the PMSG removes the need for slip rings.

The following subsections summarize the modelling of all the considered distributed generators.

2.1. Synchronous Generators

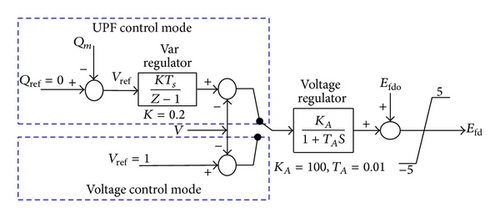
In this paper, the synchronous generator is represented by the eight-order model [8]. There are two different modes of controlling the generator excitation system. One aims to maintain its terminal voltage (constant voltage control mode) while the other one aims to maintain its power factor (constant power factor control mode) [9]. The power factor control mode is usually adopted by independent producers to maximize the active power production. The set points of voltage control and unity power factor control mode are depicted in Figure 2.

2.2. FSIG Wind Turbine

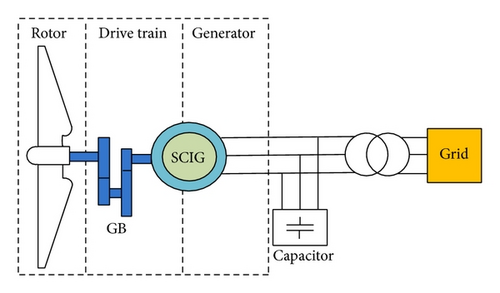
Figure 3 shows the schematic diagram of a fixed speed wind turbine, which consists of three main parts: the rotor, the drive train, and the squirrel-cage induction generator (SCIG). The dynamic models of the rotor and the drive train are given in [10]. The SCIG was represented by the fourth-order state-space model, and its mechanical parts were represented by a second-order system [8]. The generator needed reactive power was locally supplied by capacitors installed at its terminals. The capacitor capacity was adopted equal to 1/3 of the generator rated power [11].

2.3. DFIG Wind Turbine

The basic configuration of the DFIG driven by wind turbine is shown in Figure 4. The DFIG is a wound rotor induction generator, which has the same model of SCIG except that the rotor voltage does not equal zero [12].

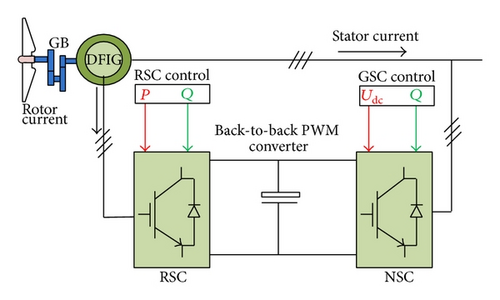
The DFIG is fed from its both stator and rotor sides. The stator is directly connected to the grid while its rotor is connected to the grid through a variable frequency AC/DC/AC converter (VFC). The VFC consists of two four-quadrant insulated-gate bipolar transistor (IGBT) pulse width modulation (PWM) converters connected back-to-back by a DC-link capacitor [13, 14].

In order to deliver an electrical power with constant voltage and frequency to the utility grid for a wide operating range of speed, from subsynchronous to supersynchronous speeds, the power flow between the generator rotor circuit and the grid must be controlled in both magnitude and direction. Connecting the rotor with the grid, via a four-quadrant AC-to-AC converter, enables the decoupling of the control of the generator active and reactive powers. Also, the variable frequency rotor voltage permits the adjustment of the rotor speed to match the optimum operating point at any practical wind speed.

The rotor side converter (RSC) and the network side converter (NSC) control circuits are shown in Figure 5, where the RSC control system consists of two basic control loops for the active and the reactive powers P and Q, respectively. The NSC is used for keeping the DC-link capacitor voltage constant regardless of the magnitude and direction of rotor power as well as controlling the NSC output reactive power especially in case of the grid disturbance.

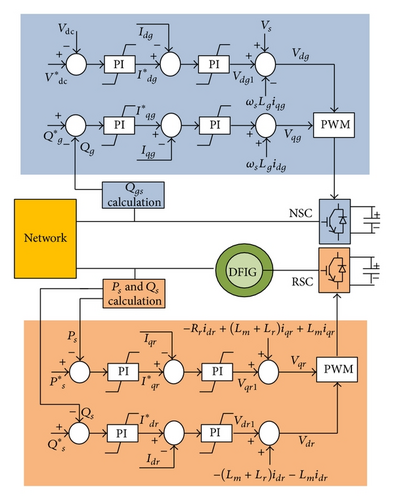
The constant power factor and constant voltage control modes, previously described in the synchronous generator subsection, will be considered with the DFIG. The constant power factor control mode can be adjusted by setting , stator reference reactive power, and , NSC reference reactive power, to zero. On the other side, the voltage control mode can be obtained by adjusting the reactive power reference to obtain a generator terminal voltage of 1 pu.

2.4. PMSG Wind Turbine

The typical configuration of the fully rated converter- (FRC-) based wind turbine is shown in Figure 6. As all the power from the wind turbine is transferred through the power converter, the specific characteristics and dynamics of the wind turbine generator are completely isolated from the power network. Hence, the electrical frequency of the generator may vary as the wind speed changes, while the network frequency remains constant, permitting the generator variable speed operation. Note that rating of the power converter for this wind turbine type is usually more than the generator rated power [14].

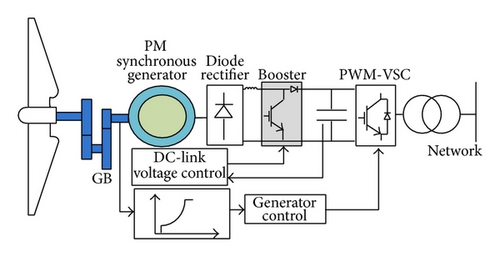
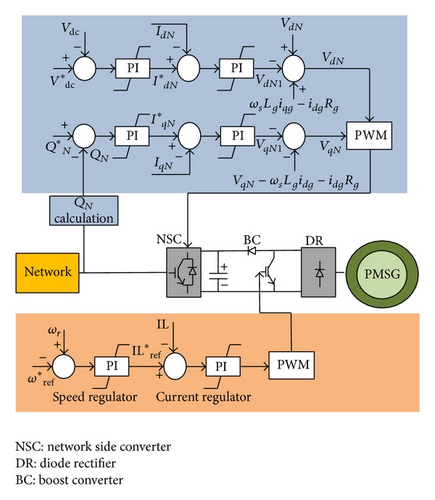
Figure 6 shows the arrangement of the PMSG with an uncontrolled diode-based rectifier as the generator side converter (GSC), DC/DC converter (DC booster), and voltage source converter (NSC) as power electronics controlled converters.

Below rated wind speed, the control objective is to track wind speed to capture and transfer the maximum power to the grid. The generator and rectifier system is uncontrolled. Therefore, the control has to be implemented by the power electronics converters, DC/DC converter (DC booster), and voltage source converter (NSC) [14].

DC/DC converters regulate the DC voltages of generator-rectifier units by varying the switching ratio so that the optimum DC voltage profile is presented at the rectifier terminal for maximum power capture operation. Meanwhile, an appropriate DC voltage is maintained at the DC bus to enable the voltage source inverters to perform the optimal real power transfer and reactive power regulation. A block diagram of the vector control of the network side converter and DC booster is shown in Figure 7.

3. Steady State Voltage Profile Computations

Before installing new DGs, utility engineers must analyze the distributor worst operating scenarios to study how the voltages at the connected loads terminals are affected by the installed DGs. These scenarios are characterized by the following [15]:

(i)
no generation and maximum load demand;
(ii)
maximum generation and maximum load demand;
(iii)
maximum generation and minimum load demand.

In this paper, it is considered that the minimum load demand corresponds to 10% of the maximum demand, and the allowable steady state voltage regulation is equal to ±5% of the supply voltage.

It is important to note that, considering the case without DG, the substation transformer tapping was adjusted to maintain the voltage values at all the feeder buses within the allowable range for minimum and maximum demands.

Now, to determine the steady state voltage profile of the considered distribution system with the considered DG types, it is assumed that a 2 MW (about 30% of the distributor total maximum load demand) DG is connected at bus 15 (see Figure 1). Considering each of the previously discussed DG types, the voltage at each of the distributor buses is determined and the results are depicted in Figure 8. Referring to Figure 8, the following can be seen:

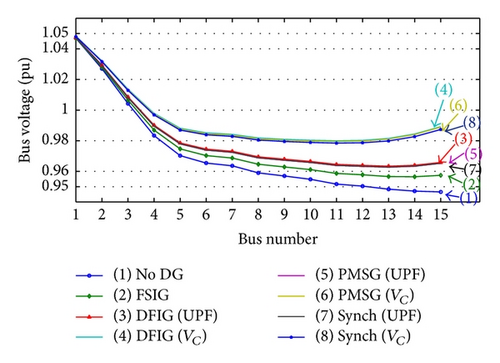
(i)
Some buses voltages will violate the superior limit during minimum demand when the unity power factor (UPF) operating mode is considered for synchronous generator, DFIG, and PMSG.
(ii)
The performance of FSIG is very close to without DG case; some buses voltages will be below the inferior limit during maximum load demand and above the superior limit during minimum load demand.
(iii)
If voltage control mode (V_C) for synchronous generator, DFIG, and PMSG is employed, then the steady state buses voltages will remain within the allowable range for both maximum and minimum load demands.

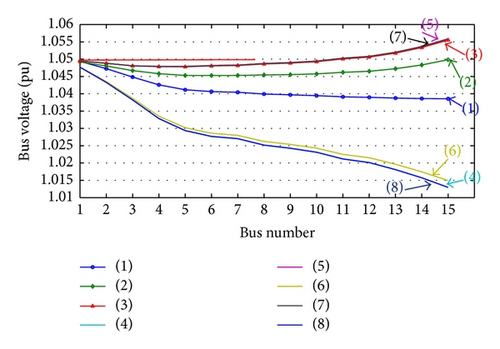
3.1. Steady State Voltage Variation due to DG Disconnection

One important issue related to the distributor steady state voltage profile is to determine how much the load buses voltages will change when the DGs are disconnected because the actuation time of voltage controllers in distribution systems, for example, under load tap change transformers, is slow. Thus, network operators want such variations to be as small as possible. In order to analyze this issue, the following global index can be utilized to quantify the impact provoked by a generator disconnection [16]:

(1)

where n_b is the total number of the distributor load buses,

is the magnitude of the load voltage at bus i with the connected DGs, and

is the bus voltage without DGs.

Assuming that the distributor DG connected to bus 15 (see Figure 1) is removed, the values of the factor VI% are computed considering the distributor maximum and minimum loading conditions. The obtained results are given in Table 1, from which the following are clear:

(i)
Greater values of VI% are obtained when each of the DFIG, PMSG, and synchronous generators is operating under voltage control condition. This essentially means that, using one of these DG types, values of the load buses voltage will be adversely affected after the generator disconnection.
(ii)
Under the distributor maximum loading condition, the loads buses voltage variation will not be greatly affected after the DG disconnection. This means that the penetration ratio increase of the DG will adversely affect the buses voltage after DG disconnection.

Table 1. Steady state voltage variation (VI%) due to DG disconnection.

Generator type	VI%
Generator type	Maximum load	Minimum load
FSIG	0.043	0.642
DFIG
UPF	1.089	0.743
Voltage control	2.276	1.368
PMSG
UPF	1.088	0.744
Voltage control	2.250	1.343
Synchronous
UPF	1.091	0.746
Voltage control	2.247	1.301

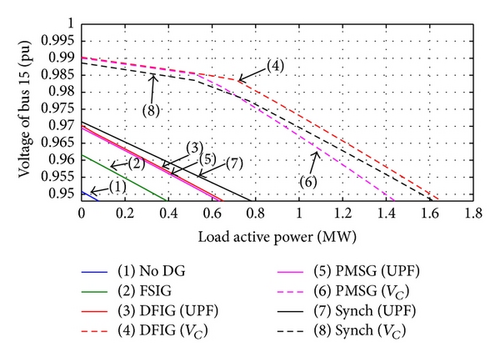
3.2. The Distribution System P_L-V_L Characteristics considering Different DGs Types

Normally, it is expected that installation of the generators close to the loads can improve the system voltage stability. However, the impact on the voltage stability depends on the reactive power exchange between the connected generator and the network, which is different from distinct DGs technologies.

In this section, the P_L-V_L characteristics of the system shown in Figure 1 are analyzed by varying the load power connected to bus 15, keeping its power factor constant, and assuming each of the DG types is connected to bus 15 with 2 MW output power. The P_L-V_L characteristics are computed until the steady state admissible voltage limit ±5% and the obtained results are depicted in Figure 9. From the obtained results, the following can be verified:

(i)
The usage of the DGs, independent of the type, increases the load power margin while maintaining the bus voltage within the admissible limits.
(ii)
The usage of the voltage control mode, with DFIG or PMSG or synchronous generator, leads to the largest power transfer because these machines provide active and reactive power to local loads.

3.3. Effects of the DGs Penetration Ratios and Their Connection Points on the Considered Distributor Steady State Voltages

In this section, it is required to investigate the penetration ratio and connection point of different DGs technologies on the considered distribution system steady state voltage. Firstly, the penetration ratios effect is illustrated by assuming that a number of DGs units each of 2 MW (30% of the distributor total maximum load value) are connected through one-by-one basis at the distributor far end bus 15; see Figure 1. For each assumed number of the connected DGs units, the buses voltages are determined considering only one of the considered DG four types. The obtained results are summarized in Table 2, from which the following are clear:

(i)
The considered distributor buses voltage regulation does not violate their admissible values (±5%), for either minimum or maximum loading, only when the connected DFIG or PMSG or synchronous generator is operating with the voltage control mode. The penetration ratio can reach twice the distributor loading without voltage violation but conductor current rating limit will be the constraint.
(ii)
Connecting only one of the DFIGs or PMSGs or synchronous generators with the UPF operating mode, the voltage regulation values at some buses will exceed its maximum admissible value for minimum loading conditions. For maximum loading condition, the number of units can reach 5 units without voltage violation.
(iii)
The utilization of local reactive power compensation with the FSIG increases the FSIG penetration ratio to three units without voltage violation.

Table 2. Maximum allowable penetration ratio of the DGs units considering steady state voltage violation.

Generator type	Number of units	Results comments
FSIG	Larger than 3 units	The min. admissible voltage regulation value is violated for max. loading condition.

DFIG, PMSG, and Synch with voltage control mode	6 units	No admissible voltage violation for either max. or min. loading conditions.

DFIG, PMSG, and Synch with UPF mode	1 unit	The max. admissible voltage regulation value is violated for min. loading condition.

Now, the connection point effect of the DGs on the distribution system load voltages is illustrated in Table 3. The FSIG, voltage control operating mode considered with DFIG, which is similar to that with PMSG and synchronous generator, and UPF operating mode with PMSG, which is similar to that with DFIG and synchronous generator, are considered in this section. Also, the DG connection points selected are buses 3, 5, 7, 9, 11, 13, and 15. At each connection point, different penetration ratios are considered (number of DG units equal to 1 or 2 or 3 or 4) with maximum loading condition only. From the obtained results, the following can be concluded:

(i)
For all cases, the connection of the DGs, despite the type, near the substation leads to the largest voltage reduction at the far end buses of the distribution system for all penetration ratios. For this connection point, the voltage violates the minimum admissible value (−5%) in italic font filled cell in Table 3.
(ii)
The best DG connection point, for improving the steady state voltage profile, is found to be close to the far end of the considered distribution system.
(iii)
At each connection point, the DGs penetration ratios have a little effect on the steady state voltage profile.
(iv)
The high penetration ratios of the FSIG connected at the end of the distribution system lead to voltage violation.
(v)
Also, for large penetration ratios, the UPF operating mode will lead to voltage violation (this does not appear in Table 3) similar to that mentioned in Table 2.

Table 3. DGs connection point and penetration ratio effect on the distribution system steady state voltages.

DG PCC	Number of DG units	FSIG		⁢V_C with DFIG		⁢UPF with PMSG
DG PCC	Number of DG units	V_min	At bus	V_min	At bus	V_min	At bus
Bus 3	1	0.948	15	0.947	15	0.949	15
	2	0.950	15	0.948	15	0.953	15
	3	0.952	15	0.948	15	0.956	15
	4	0.954	15	0.948	15	0.959	15

Bus 5	1	0.951	15	0.961	15	0.954	15
	2	0.955	15	0.968	15	0.961	15
	3	0.959	15	0.971	15	0.968	15
	4	0.962	15	0.973	15	0.973	15

Bus 7	1	0.951	15	0.966	15	0.955	15
	2	0.956	15	0.973	15	0.963	15
	3	0.960	15	0.977	15	0.971	15
	4	0.963	15	0.979	15	0.977	15

Bus 9	1	0.952	15	0.970	15	0.957	15
	2	0.959	15	0.979	15	0.966	15
	3	0.962	15	0.983	15	0.975	15
	4	0.965	15	0.985	15	0.982	15

Bus 11	1	0.953	15	0.975	15	0.959	15
	2	0.960	15	0.984	15	0.970	15
	3	0.964	15	0.988	15	0.979	15
	4	0.966	15	0.990	15	0.987	15

Bus 13	1	0.954	15	0.979	15	0.961	15
	2	0.961	15	0.987	13	0.973	15
	3	0.965	15	0.989	12	0.982	10
	4	0.965	15	0.989	12	0.986	9

Bus 15	1	0.955	14	0.977	11	0.962	13
	2	0.959	13	0.981	11	0.972	12
	3	0.959	13	0.982	10	0.977	11
	4	0.948	13	0.979	10	0.978	10

4. Short Duration Voltage Variations Profile

The short duration voltage variation can be defined as a change of the rms voltage value, at the power frequency, for a duration from 0.5 cycles to 1 min [17, 18]. The voltage variations are classified into three types as follows:

(i)
The voltage swell: when the voltage value varies from 1.10 pu to 1.80 pu.
(ii)
The voltage sag: when the voltage value varies from 0.10 pu to 0.90 pu.
(iii)
The voltage interruption: when the voltage value decreases to less than 0.10 pu.

The incidences of short duration voltage variations in distribution networks are relatively frequent. During short circuits, connection of a large load and disconnection of large capacitor voltage sags may occur at the system buses. On the other hand, the single line to ground faults or disconnection of large loads or connection of large capacitors may lead to voltage swells. Interruptions can be the result of power system faults, equipment failures, intermittent loose connections in power wiring, and control malfunctions.

The presence of DGs may influence the magnitude and the duration of the voltage sags, swells, and interruptions. It will depend on the impact of these generators on the system short-circuit level and the dynamic behaviour of the reactive power exchange between the generator and the network. In this section, the DGs performance during voltage sag, swell, and interruption is studied.

4.1. Voltage Sag Magnitude and Duration due to Large Inductive Load Connection

In this subsection, the behaviour of the different DGs types during a large induction motor starting is studied. An induction motor is assumed to be connected to bus 13 of the considered distributor and each of the previously mentioned DGs types is assumed to be connected to bus 15.

The results are obtained in Figure 10, from which the following are clear:

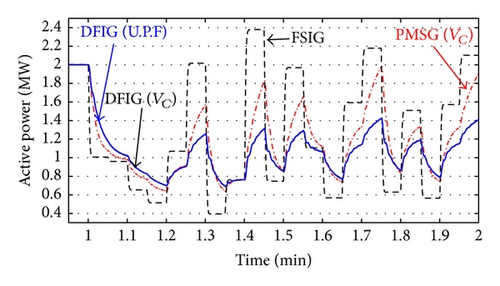
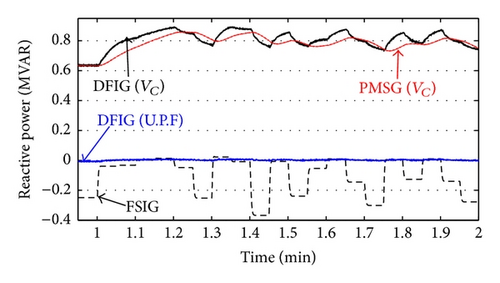
(i)
The voltage control operation mode of the DFIG, PMSG wind turbine, and synchronous generator can reduce the voltage sag magnitude and duration.
(ii)
Although the unity power factor operation mode (used with synchronous generator in this case) does not exchange reactive power with distribution system, the voltage profile is better than without DG and FSIG cases.

Now, it is required to determine the effect of the DG connection point on the voltage sag magnitude and duration. Therefore, it is assumed that each of the considered DGs (of 2 MW output power) is connected to buses 15, 13, 11, and 9 while the induction motor is still connected to bus 13. The minimum voltage value and the voltage sag duration, at which the bus voltage is less than 0.9 pu, of bus 15 are listed in Table 4. From the obtained results, the following are found:

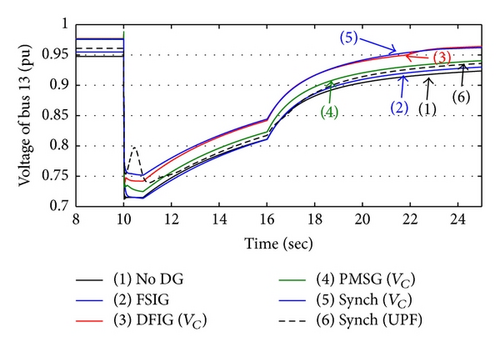
(i)
The utilization of DGs, despite the type and location, reduces the voltage sag problem.
(ii)
The DG connection point affects the voltage sag magnitude and duration.
(iii)
The connection of the DGs downstream inductive load connection point enhances the system voltage (magnitude and sag duration) versus upstream connection except the voltage magnitude when the FSIG is utilized.
(iv)
The voltage control operating mode presents the best performance followed by unity power factor (used with synchronous generator in this case) and finally the FSIG.

Table 4. Effect of DG connection point on the voltage sag magnitude and duration at bus 15.

Connection bus of DG	FSIG	DFIG	PMSG	Synch
Connection bus of DG	FSIG	DFIG	PMSG	V_C	UPF
Minimum voltage sag (0.71 pu without DG)
15	0.713	0.746	0.729	0.767	0.746
13	0.713	0.739	0.724	0.753	0.734
11	0.714	0.735	0.723	0.746	0.729
9	0.715	0.731	0.722	0.739	0.725

Voltage sag duration (9.66 sec without DG)
15	8.95	6.95	7.95	6.96	8.66
13	9.04	7.29	8.22	7.32	8.78
11	9.08	7.48	8.36	7.47	8.81
9	9.14	7.69	8.51	7.66	8.88

4.2. DGs Types Effect on the Distributor Voltage Interruption

Because most faults on distribution system are transient, the power can be successfully restored within several cycles after the current interruption. Thus, most automatic circuit breakers are designed to reclose 2 or 3 times, if needed, in rapid succession. The multiple operations are designed to permit various sectionalizing schemes to operate and to give some more persistent transient faults a second chance to clear. There are special circuit breakers for utility distribution systems called “reclosers” that were designed to perform the fault interruption and reclose function particularly well.

The isolated area from recloser operation is subjected to voltage interruption. The duration of voltage interruptions depends on the recloser operation characteristics. Figure 11 shows the common reclosing sequences used in many utilities which represent 1-fast, 3-delayed operation [18, 19]. In case of temporary faults, which frequently occurred in distribution system as a SLG fault, a voltage sag and swell will occur for a duration of 3 to 6 cycles followed by three-phase voltage interruption. After the elapsing of 1 to 2 sec from the voltage interruption occurrence, the reclosing process returns the isolated area to the main distribution system.

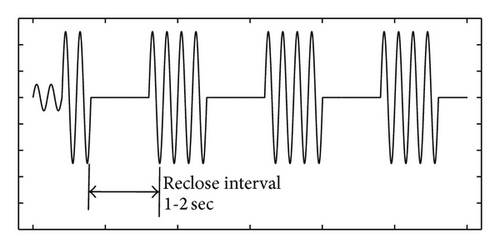
The presence of DGs in the isolated area may affect the area voltage interruption depending on the DG capability of supplying active and reactive power.

In this section, the response of each of the considered DGs when a SLG fault occurs at a point on the distributor is studied considering the reclosing operation. A SLG fault is assumed to occur at the time 0.5 sec at a point close to bus 8 when the DG, of 2 MW, is connected to bus 15. The assumed fault is removed after the elapsing of 0.16 sec (i.e., 8.0 cycles fault duration), at t = 0.66 sec. A line recloser is assumed to be located near bus 7, nearly at the midpoint of the distributor length, and it is opened after 0.12 sec from the fault instant (6 cycles after fault occurrence), at t = 0.62 sec. The recloser is still open for 2.0 sec from the opening instant. The obtained results are obtained in Figure 12 from which the following can be concluded:

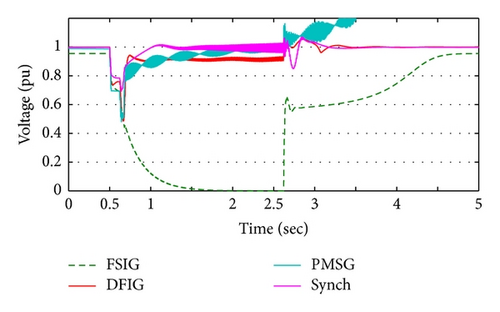
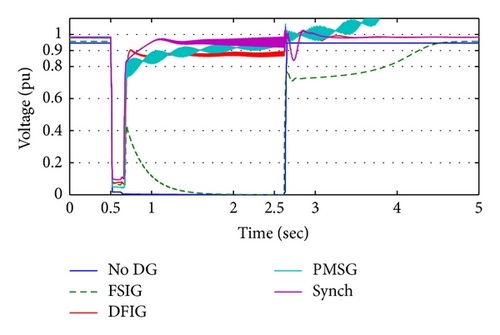
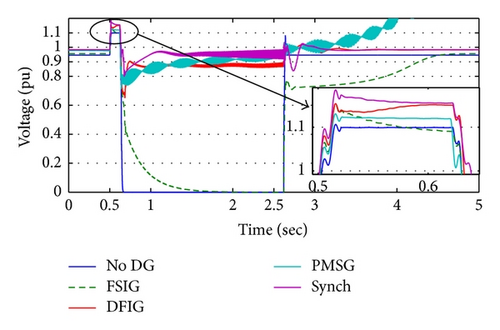
(i)
DFIG wind turbine and conventional synchronous generator can maintain the load voltage of the isolated area within the normal limit (±5%) during the recloser opening, preventing the interruption.
(ii)
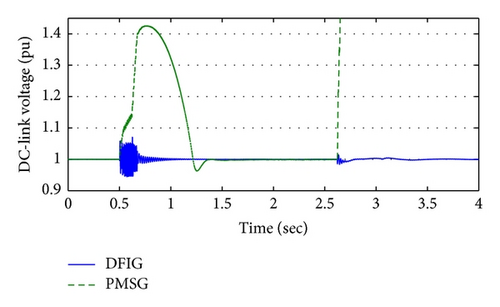
Although the PMSG can restore the isolated area voltage after fault removing to an acceptable value, it cannot keep it stable (a, b, and c) because of the incapability of DC-link voltage restoration (d).
(iii)
In the case of the FSIG, it is noted that the isolated area is subjected to voltage interruption followed by voltage sag, which is worse than without DG case.
(iv)
The occurrence of the SLG fault leads to a voltage swell on the unfaulted phases (c), where the DG utilization increases the voltage swell problem slightly.

5. Voltage Fluctuation and Flicker

One of the important power quality problems is the voltage flicker, which is the result of voltage fluctuations. Grid-connected wind turbines may have considerable fluctuations in the output powers, which depend on the wind turbine type. The power generated by the wind turbine fluctuates as it is much more variable than that produced by conventional generators.

From a signal analyzing point of view, the voltage flicker is defined as a low-frequency (5 : 15 Hz) modulation of the network voltage at 60/50 Hz and the flickermeter is used to separate the carrier from the modulating wave and weigh the effects of the latter based on human sensitivity to the disturbance and generate the instantaneous sensation of the flicker S(t) and the short-term flicker P_st. The IEC flickermeter is developed in Matlab/Simulink, as shown in Figure 13, and is used to calculate S(t) and P_st [20–22]. The admissible limit of the flicker produced by the distributed generators on the MV grid is 0.35 for P_st [23].

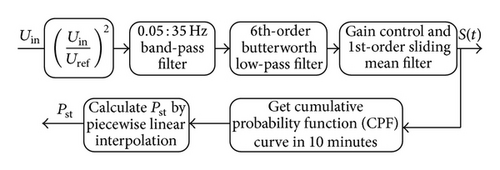
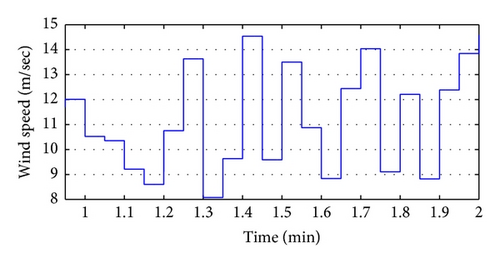
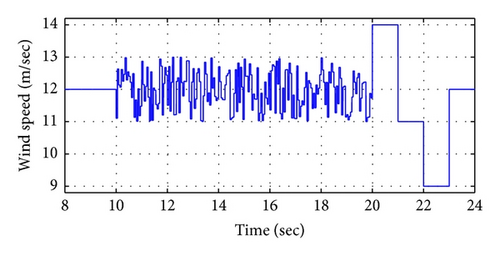
Two case studies are considered in this section. The first case studied the voltage flicker resulting from the different wind turbine types assuming wind speed variations. In the second case study, it is assumed that a constant wind speed and the voltage flicker resulted from a connected pulsating load.

Now, considering the first case study, it is assumed that the steep wind speed variation, shown in Figure 14, is applied to each of the considered wind turbines. The wind turbine of the 2.0 MW rated power is assumed to be connected at bus 15. Figure 15 shows the performance of the three considered wind turbines generators. The instantaneous voltage flicker across the wind turbine PCC is shown in Figure 16 while the corresponding average short-term flicker values are given in Table 5. From the obtained results, the following are clear:

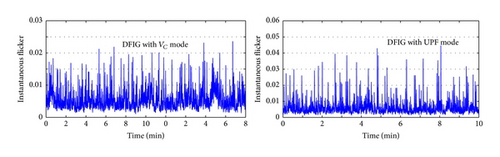
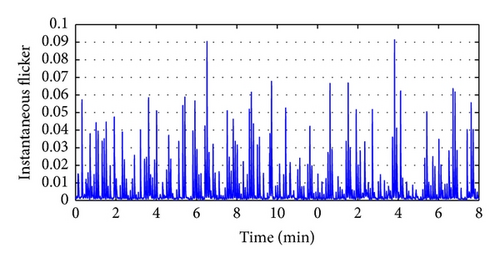
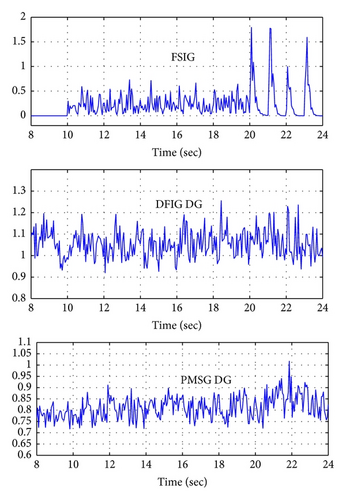
(i)
The active and reactive power change profile of the FSIG increases the distribution system flicker. The steep change of output active power and reactive power leads to a voltage fluctuation with unacceptable flicker sensation (P_st = 0.464 which is greater than the limit, that is, 0.35).
(ii)
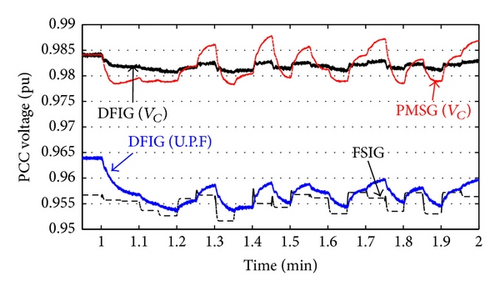
Despite reactive power controllability of both DFIG and PMSG with voltage control operating mode, the DFIG performance is more acceptable than the PMSG. The two paths of active and reactive power control in DFIG (RSC and NSC) are leading to smooth change in the DFIG output active and reactive power and terminal voltage as compared with the PMSG.

Table 5. Average short-term flicker P_st for a duration of 10 minutes at bus 15.

FSIG

DFIG

PMSG

V_C

UPF

0.464

0.322

0.368

0.328

Now, assuming a constant wind speed, the performance of the DGs under variable load condition will be studied in this section. The load variation shown in Figure 17 is assumed to be at bus 13. The short-term flicker P_st at buses 9, 11, 13, and 15 is listed in Table 6 for different connection points of each DG. From the obtained results, the following are found:

(i)
The utilization of the DGs, despite the type and connection point, reduces the distribution system voltage short-term flicker.
(ii)
The connection of the DGs, despite the type, upstream pulsating load connection point increases the system voltage short-term flicker at all the considered distribution buses.
(iii)
The connection of the DGs downstream variable load (at bus 15), or at its terminal (at bus 13), reduces the voltage flicker at all the considered distribution buses.
(iv)
The voltage control of the synchronous generator can reduce the voltage variation (V_max − V_min) so the voltage flicker is reduced compared with other DGs.
(v)
The UPF operating mode, used with DFIG in this case, can be considered the worst case for all connection points among all considered DGs technologies.
(vi)
Although the DFIG and PMSG operate with voltage control mode, the voltage variation (V_max − V_min) is larger than that in case of FSIG.

Table 6. Average short-term flicker P_st at buses 9, 11, 13, and 15 for different connection points of the considered DGs.

Bus number	Without DG	FSIG	DFIG		PMSG V_C	Synch V_C
Bus number	Without DG	FSIG	V_C	UPF	PMSG V_C	Synch V_C
DG connected at bus 9
9	0.938	0.687	0.727	0.753	0.745	0.487
11	1.289	0.990	1.017	1.051	1.041	0.726
13	1.736	1.385	1.391	1.433	1.421	1.045
15	1.735	1.384	1.390	1.432	1.420	1.044

DG connected at bus 11
9	0.938	0.629	0.701	0.723	0.718	0.439
11	1.289	0.892	0.978	1.014	1.001	0.613
13	1.736	1.268	1.343	1.391	1.375	0.906
15	1.735	1.266	1.342	1.390	1.374	0.904

DG connected at bus 13
9	0.938	0.570	0.670	0.691	0.685	0.392
11	1.289	0.808	0.935	0.968	0.956	0.547
13	1.736	1.130	1.286	1.337	1.313	0.752
15	1.735	1.129	1.285	1.336	1.312	0.751

DG connected at bus 15
9	0.938	0.579	0.664	0.692	0.677	0.407
11	1.289	0.821	0.928	0.970	0.947	0.569
13	1.736	1.149	1.279	1.339	1.304	0.783
15	1.735	1.100	1.282	1.347	1.299	0.674

6. Harmonic Distortion

The harmonic current distortion in the distribution system is generated by the nonlinear loads interacting with power system impedance and gives rise to the harmonic problems. The effect of harmonics in the power system can lead to degradation of power quality at the consumer’s terminal, increase of power losses, and malfunction in communication system. The degree of variation is assessed at the PCC, where consumer and supplier areas of responsibility meet. Wind turbines DGs can also contribute to the harmonic distortion of the voltage waveform. In the first edition of IEC 61400-21, only wind turbines with power converters should be tested for harmonics. However, this will probably be changed in the second edition, requiring measurements of harmonic currents for all types of wind turbines [24–26].

According to [2], when the DG is serving balanced linear loads, harmonic current injection at the PCC should not exceed the limits stated in Table 7. Therefore, it is required to determine the current and voltage harmonic distortion produced from each wind turbine during constant and variable wind speed. The wind speed profile shown in Figure 18 is applied to the rotor of different wind turbine types (each of 2 MW rated power) connected to bus 15; see Figure 1. The TDD of wind turbines injected current is shown in Figure 19 and the voltage THD at the wind turbine connection point “bus 15” is shown in Figure 20. From the obtained results, the following can be concluded:

(i)
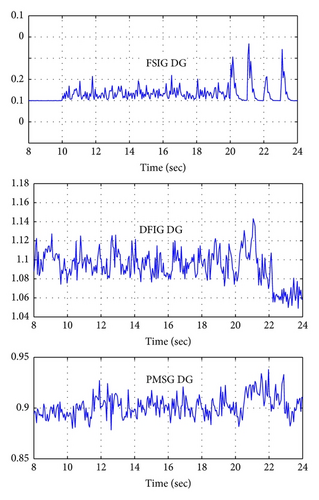
For constant or variable wind speed, the values of the injected current TDD and the terminal voltage THD are within the admissible range.
(ii)
Only the FSIG is affected with wind speed variation, where the TDD and THD nearly equal zero for constant wind speed region (t < 10 sec).

Table 7. Maximum allowable harmonic distortion at the DG PCC.

Total Demand Distortion (TDD) of the DG injected current	Total Harmonic Distortion (THD) at the DG PCC
5.0%	5.0%

Now, it is required to determine the effect of nonlinear load on the voltage THD of the distribution system containing the previously mentioned DGs. The input mechanical power of the DGs is assumed, in this case, to be constant. Also, the effect of DG connection point is determined. Figure 21 shows the voltage and current at bus 13 to which the nonlinear load is connected. Figure 22 shows the voltage THD at the distribution system different buses at different connection points of each DG. From the obtained results, the following can be concluded:

(i)
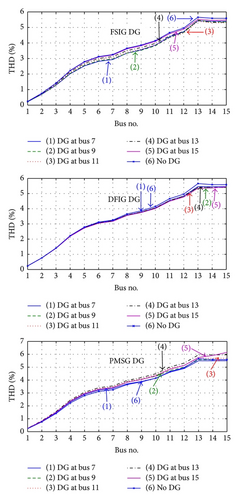
Despite the DG type, the THD nearly does not change after wind turbine DG connection.
(ii)
The connection point of the wind turbine DG has no effect on the voltage THD.

7. DGs Penetration Ratio and Connection Point Effect on the Distributor Losses

Although the active power losses in the distribution system are not a technical power quality factor that can limit the amount of the penetrated DGs, they are considered as an important economical factor [17]. Therefore, in this section, the active power losses of the distribution system, shown in Figure 1, are determined for different scenarios of the connected DGs and their connection points.

Firstly, each of the considered DG types is assumed to be connected to bus 15 and the distributor active power losses are calculated assuming different penetration ratios and loading condition. The results are presented in Table 8. The values of the active power losses for the case without DGs are also shown. From the obtained results, the following can be concluded:

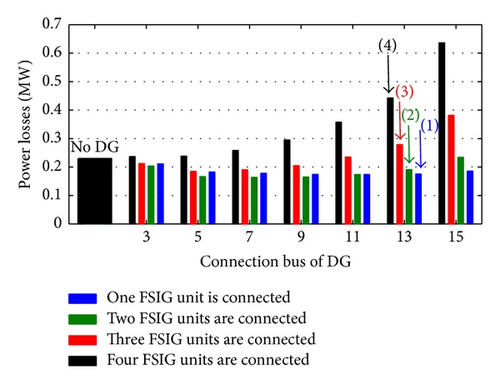
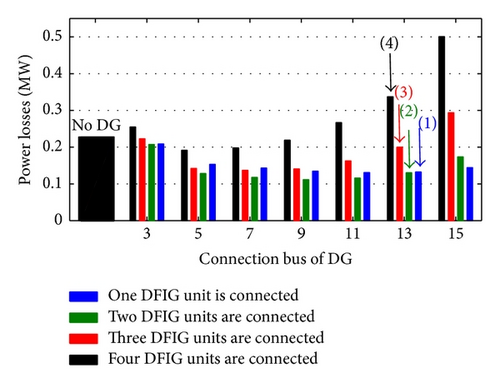
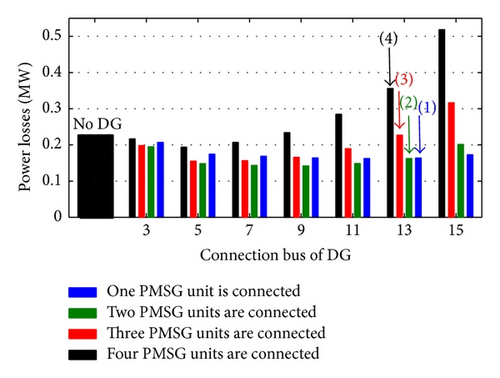
(i)
For Maximum Loading Condition. The adoption of voltage control operation mode (with DFIG, PMSG, and Synch generator) leads to the largest reduction of power losses because these generators can supply the active and reactive loads locally, decreasing the magnitude of the distribution feeders current. On the other hand, the usage of FSIG does not cause a great reduction in the active power losses. In this case, the generator consumes reactive power from the network, raising the magnitude of the currents circulating in the feeders. The losses behaviour in the presence of unity power factor (with synchronous generators in this case) is situated between the other two cases because these generators supply locally active power but do not provide or consume reactive power.
(ii)
For Minimum Loading Condition. The presence of the DGs increases the active power losses, independent of the generator employed. In this situation, a large amount of active power generated is exported to the substation, adversely influencing the distribution system losses. The usage of the voltage control operating mode can be related to the worst case under losses viewpoint because the generator consumes a large amount of reactive power to keep the terminal voltage at 1 pu.

Table 8. Active power losses (in MW).

Number of turbines	FSIG	DFIG	PMSG	Synch
Number of turbines	FSIG	DFIG	PMSG	V_C	UPF
Maximum demand (losses without DG equal 0.2277)
1	0.1855	0.1445	0.1491	0.1501	0.1728
2	0.2342	0.1737	0.1787	0.1803	0.2016
3	0.3817	0.2939	0.3015	0.3037	0.3166
4	0.6367	0.5007	0.5129	0.5159	0.5183

Minimum demand (losses without DG equal 0.0027)
1	0.0428	0.0642	0.0579	0.0686	0.0402
2	0.1597	0.2060	0.2116	0.2169	0.1497
3	0.3530	0.4263	0.4380	0.4458	0.3285
4	0.6267	0.7237	0.7424	0.7616	0.6167

Now, to determine the effect of the DG connection point on the distributor active power losses, it is assumed that the DG is connected to buses 3, 5, 7, 9, 11, 13, and 15. At each connection point, different penetration ratios are considered. The considered DGs are the FSIG, the DFIG with voltage control operating mode, and the PMSG with UPF operating mode. The results are shown in Figure 23 from which the following can be concluded:

(i)
The minimization of power losses depends, explicitly, on the connection point of the DG and its penetration ratios.
(ii)
For small penetration ratios, the suggested connection point of any one of the considered wind turbine DGs is near the far end of the distribution system. With penetration ratio increase, the suitable DG connection point comes near the substation side.
(iii)
The use of voltage control mode with DFIG or PMSG reduces the power losses despite the connection point or the DG penetration ratio.

8. Conclusions

In this paper, a comprehensive study of the power quality problems for a considered 15-bus radial distribution system with embedded DGs has been introduced. The power quality studies are carried out in a comparison aspect between the conventional synchronous generator, as DGs are widely in use at present, and the different wind turbines technologies, which represent the foresightedness of the DGs. The absence of DGs is assumed as a base case for the studies. From the results obtained in this paper, the following conclusions have been obtained:

(1)
The utilization of the DGs may be one of the power quality enhancement methods according to some factors such as the DG type, operating mode, penetration value, and connection point.
(2)
The wind turbine DGs-based DFIG and PMSG with voltage control mode have nearly the same performance of conventional synchronous generator during steady state and transient operating conditions.
(3)
The penetration ratio of wind turbine DGs operating with voltage control mode can reach 100% maximum distribution system loading without violating the admissible voltage in the steady states or losing system stability during transient conditions.
(4)
The power quality of the distribution system is very sensitive to the connection point of the embedded DGs, where the following are considered:
- (i)
  The distribution system load voltage improvement, in the steady state, requires a connection of the DG near the far end of the distributor despite its penetration.
- (ii)
  Active power losses minimization depends, significantly, on the DG connection point and its penetration ratio. The connection point should be near the distribution far end for minimum penetration ratios and must be transposed forward the main substation with penetration ratio increase.
- (iii)
  The voltage sag problem can be reduced by connecting the DG downstream source of voltage sag problem.
- (iv)
  The voltage interruption problem can be solved by suitable connection of the DG with respect to protection systems. The DFIG wind turbine with voltage control mode can prevent the voltage interruption in the distribution isolated area similar to synchronous generators.
- (v)
  The connection of the DG, despite its type, downstream voltage flicker sources reduces the voltage flicker problem at all distribution system buses.
- (vi)
  The THD produced from the nonlinear loads is not affected by the DG, despite its type and connection point.
(5)
The voltage flicker due to wind turbine variable output power is still within acceptable limits until with pulsating wind speed variation.
(6)
The main problem of the FSIG wind turbine DG appears manifestly during transient conditions due to the lack of reactive power support.
(7)
The DC-link of the DFIG and PMSG represents the main challenge of these wind turbine operations during transient conditions.
(8)
The disconnection of the wind turbine DGs during system faults listed in interconnecting distributed resources with electric power systems standard must be restudied as well as the ability of coordination between the protection devices and the wind turbine control system.

Competing Interests

The authors declare that they have no competing interests.

Appendix

In this section, the systems data are presented.

(A) Line data in ohm:
- Z_1-2: 0.1114 + j0.3340
- Z_2-3: 0.1310 + j0.3930
- Z_3-4: 0.1572 + j0.4716
- Z_4-5: 0.1048 + j0.3144
- Z_5-6: 0.0590 + j0.1769
- Z_6-7: 0.0236 + j0.0707
- Z_7-8: 0.0707 + j0.2122
- Z_8-9: 0.0354 + j0.1061
- Z_9-10: 0.0482 + j0.1446
- Z_10-11: 0.0844 + j0.2530
- Z_11-12: 0.0482 + j0.1446
- Z_12-13: 0.0985 + j0.2954
- Z_13-14: 0.1231 + j0.3693
- Z_14-15: 0.1539 + j0.4616.
(B) Load data in KVA:
- Load 2: 133.3 + j100
- Load 3: 1466.7 + j1100
- Load 4: 266.7 + j200
- Load 5: 1600 + j1200
- Load 6: 266.7 + j200
- Load 7: 400 + j300
- Load 8: 266.7 + j200
- Load 9: 533.3 + j400
- Load 10: 266.7 + j200
- Load 11: 400 + j300
- Load 12: 266.7 + j200
- Load 13: 400 + j300
- Load 14: 266.7 + j200
- Load 15: 133.3 + j100.
(C) Transformer (T1) data:
- 8 MVA 66/11 kV Δ/Y_g
- R₁ = R₂ = 0.002 pu
- X₁ = X₂ = 0.02 pu
- R_m = X_m = 500 pu.
(D) Transformer (T2) data:
- 2.2 MVA 11/0.575 kV Δ/Y_g
- R₁ = R₂ = 0.002 pu
- X₁ = X₂ = 0.02 pu
- R_m = X_m = 500 pu.
(E) FSIG wind turbine (2 MVA) data:
- R_s = 0.016 pu
- L_ls = 0.060 pu
- pu
- pu
- L_m = 3.50 pu
- H_g = 0.700 s
- H_T = 4.000 s.
(F) DFIG wind turbine (2 MVA) data:
- R_s = 0.023 pu
- L_ls = 0.180 pu
- pu
- pu
- L_m = 2.90 pu
- H_g = 0.685 s
- H_T = 4.32 s
- C_DC-link = 10000 μf
- V_dc-nominal = 1150.
(G) PMSG wind turbine (2 MVA) data:
- R_s = 0.006 pu
- L_ls = 0.180 pu
- H_g = 0.62 s
- H_T = 4.32 s
- C_DC-link = 90000 μf
- V_dc-nominal = 1100.
(H) Synchronous generator (2 MVA) data:
- X_d = 1.400 pu
- X_q = 1.372 pu
- pu
- pu
- pu
- pu
- X_l = 0.050 pu
- R_a = 0.00014 pu
- s
- s
- s
- s
- H = 1.5 s.

References

1 IEC Standards, Testing and measurement techniques—power quality measurement methods, 2008, no. IEC Std 61000-4-30.
Google Scholar
2 IEEE Standard, Interconnecting distributed resources with electric power systems, IEEE Std, 2003, no. 1547-2003, https://doi.org/10.1109/IEEESTD.2003.94285.
10.1109/IEEESTD.2003.94285
Google Scholar
3 Lin T. and Domijan A., On power quality indices and real time measurement, IEEE Transactions on Power Delivery. (2005) 20, no. 4, 2552–2562, https://doi.org/10.1109/TPWRD.2005.852333, 2-s2.0-27844577319.
10.1109/TPWRD.2005.852333
Web of Science® Google Scholar
4 Almeida C. F. M. and Kagan N., Harmonic state estimation through optimal monitoring systems, IEEE Transactions on Smart Grid. (2013) 4, no. 1, 467–478, https://doi.org/10.1109/TSG.2012.2235472, 2-s2.0-84875051942.
10.1109/TSG.2012.2235472
Web of Science® Google Scholar
5 Shin Y.-J., Powers E. J., Grady M., and Arapostathis A., Power quality indices for transient disturbances, IEEE Transactions on Power Delivery. (2006) 21, no. 1, 253–261, https://doi.org/10.1109/tpwrd.2005.855444, 2-s2.0-33244466470.
10.1109/TPWRD.2005.855444
Web of Science® Google Scholar
6 Long C., Farrag M. E. A., Zhou C., and Hepburn D. M., Statistical quantification of voltage violations in distribution networks penetrated by small wind turbines and battery electric vehicles, IEEE Transactions on Power Systems. (2013) 28, no. 3, 2403–2411, https://doi.org/10.1109/TPWRS.2013.2252472, 2-s2.0-84880920283.
10.1109/TPWRS.2013.2252472
Web of Science® Google Scholar
7 Shi L., Sun S., Yao L., Ni Y., and Bazargan M., Effects of wind generation intermittency and volatility on power system transient stability, IET Renewable Power Generation. (2014) 8, no. 5, 509–521, https://doi.org/10.1049/iet-rpg.2013.0028, 2-s2.0-84904017013.
10.1049/iet-rpg.2013.0028
Web of Science® Google Scholar
8 Kundur P., Power System Stability and Control, 1994, McGraw-Hill, New York, NY, USA.
Google Scholar
9 Hurley J. D., Bize L. N., and Mummert C. R., The adverse effects of excitation system var and power factor controllers, IEEE Transactions on Energy Conversion. (1999) 14, no. 4, 1636–1641, https://doi.org/10.1109/60.815117, 2-s2.0-0033315473.
10.1109/60.815117
Web of Science® Google Scholar
10 Fernández L. M., Saenz J. R., and Jurado F., Dynamic models of wind farms with fixed speed wind turbines, Renewable Energy. (2006) 31, no. 8, 1203–1230, https://doi.org/10.1016/j.renene.2005.06.011, 2-s2.0-32044467173.
10.1016/j.renene.2005.06.011
Web of Science® Google Scholar
11 Jenkins N., Allan R., Crossley P., Kirschen D., and Strbac G., Embedded Generation, 2000, 1st edition, Institution of Electrical Engineers, London, UK.
10.1049/PBPO031E
Google Scholar
12 Kawady T. A., Shaaban H., and El-Sherif A., Investigation of grid-support capabilities of doubly fed induction generators during grid faults, Proceedings of the IET Conference on Renewable Power Generation (RPG ′11), September 2011, Edinburgh, Scotland, paper 11.3.4, https://doi.org/10.1049/cp.2011.0234, 2-s2.0-84856257274.
10.1049/cp.2011.0234
Google Scholar
13 Ekanayake J. B., Holdsworth L., Wu X., and Jenkins N., Dynamic modeling of doubly fed induction generator wind turbines, IEEE Transactions on Power Systems. (2003) 18, no. 2, 803–809, https://doi.org/10.1109/TPWRS.2003.811178, 2-s2.0-0038519499.
10.1109/TPWRS.2003.811178
Web of Science® Google Scholar
14 Lara O., Jenkins N., Ekanayake J., Cartwright P., and Hughes M., Wind Energy Generation Modeling and Control, 2009, John Wiley & Sons.
Google Scholar
15 Masters C. L., Voltage rise: the big issue when connecting embedded generation to long 11 kv overhead lines, Power Engineering Journal. (2002) 16, no. 1, 5–12, https://doi.org/10.1049/pe:20020101, 2-s2.0-0036465326.
10.1049/pe:20020101
Web of Science® Google Scholar
16 Freitas W., Vieira J. C. M., Morelato A., da Silva L. C. P., da Costa V. F., and Lemos F. A. B., Comparative analysis between synchronous and induction machines for distributed generation applications, IEEE Transactions on Power Systems. (2006) 21, no. 1, 301–311, https://doi.org/10.1109/TPWRS.2005.860931, 2-s2.0-32144458236.
10.1109/TPWRS.2005.860931
Web of Science® Google Scholar
17 Borges C. L. T. and Falcao D. M., Impact of distributed generation allocation and sizing on reliability, losses and voltage profile, 2, Proceedings of the IEEE Bologna Power Tech Conference, June 2003, https://doi.org/10.1109/PTC.2003.1304342.
10.1109/PTC.2003.1304342
Google Scholar
18 IEEE, IEEE recommended practice for monitoring electric power quality, IEEE Standard, 2009, no. 1159.
Google Scholar
19 Dugan R., Granaghan M., Santoso S., and Beaty H., Electrical Power Systems Quality, 2004, McGraw-Hill.
Google Scholar
20 IEC Standards, IEC 61000-4-15: Testing and Measurement Techniques—Flickermeter. Functional and Design Specifications, 2012, 77, IEC Technical Committee.
Google Scholar
21 Gutierrez J., Ruiz J., Leturiondo L., and Lazkano A., Flicker measurement system for wind turbine certification, IEEE Transactions on Instrumentation and Measurement. (2009) 58, no. 2, 375–382.
Web of Science® Google Scholar
22 IEC, Power performance measurements of electricity producing wind turbines, IEC, 2005, no. 61400-12-1, IEC Technical Committee 88.
Google Scholar
23 Naslin C., Gonbeau O., Fraisse J. L., and Thai T. C., Wind farm integration-power quality management for French distribution network, Proceedings of the 18th International Conference and Exhibition on Electricity Distribution (CIRED ′05), June 2005, Turin, Italy, 1–5, https://doi.org/10.1049/cp:20051036.
10.1049/cp:20051036
Google Scholar
24 IEC, Testing and measurement techniques—general guide on harmonics and interharmonics measurements and instrumentation, for power supply systems and equipment connected thereto, IEC Standard, 2009, no. 61000-4-7, edition 2.1.
Google Scholar
25 IEEE Standards, IEEE recommended practices and requirements for harmonic control in electrical power systems, IEEE Std, 1992, no. 519.
Google Scholar
26 IEC Standards, Recommendations for preparing the measurements and assessment of power quality characteristics of wind turbines, 2001, no. IEC Std 61400-21.
Google Scholar

Citing Literature

All articles

Power Quality Investigation of Distribution Networks Embedded Wind Turbines

Abstract

1. Introduction