We investigate the transmission properties of a metallic layer with narrow slits. We consider (time-harmonic) Maxwell’s equations in the H-parallel case with a fixed incident wavelength. We denote η > 0 as the typical size of the complex structure and obtain the effective equations by letting η → 0. For metallic permittivities with negative real part, plasmonic waves can be excited on the surfaces of the slits. For the waves to be in resonance with the height of the metallic layer, the corresponding results can be perfect transmission through the layer.

1. Introduction

Negative refraction of electromagnetic waves in metamaterials has become of major interest in recent years, compare [1, 2], especially to construct small scale optical devices for technical applications in the fields of micro- and nanooptics. Metamaterials are the materials that are not found in nature; instead they are created by the composition of several metals or plastics or both. Due to their precise shape, size, geometry, and arrangement of metals, these metamaterials are capable of influencing the electromagnetic waves by absorbing, bending, or refracting. To create the metamaterials, the composite materials are arranged in repeated (periodic) fashion with periodicity scales smaller than the wavelength of waves. Negative index metamaterial or negative index material (NIM) is a metamaterial where the refractive index (in optics theory, the refractive index of a material is a dimensionless number which describes how light propagates through that medium and is defined as the ratio c/υ, where c is the speed of light in vacuum and υ is the phase velocity of light in the medium) has a negative value over some frequency range when an electromagnetic wave passes through it. Negative index materials are extensively studied in the fields on optics, electromagnetics, microwave engineering, material sciences, semiconductor engineering, and several others.

In this work, we study the phenomena of light wave passing through the subwavelength metallic structure; that is, we investigate the high transmission of light wave through a metamaterial with thin holes inside it. We consider a thin metallic structure (inside a medium) with holes smaller than the wavelength of incident photon which shows the high transmission of light waves through this metallic structure. This high transmission contradicts the classical aperture theory and shows an important feature of metamaterials. To demonstrate the geometry assumed in this work, let us consider Figure 1 where the light wave emerging from a source (l.h.s of the figure) is passing through a metamaterial with negative refractive index and its image is given on the r.h.s. (cf. this figure to that of [3]).

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

The light wave is originating from the left side and is getting refracted through the metallic plate and its image is on the right (this image is taken from [2]).

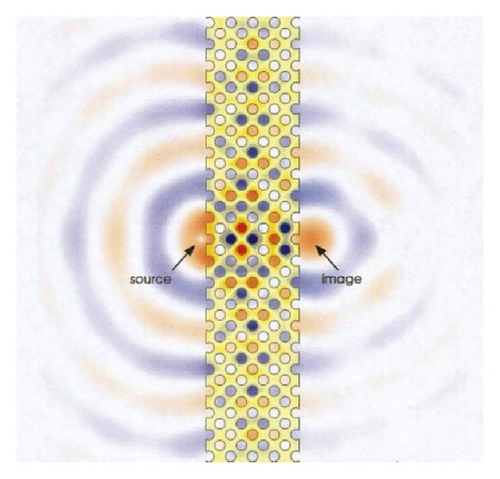
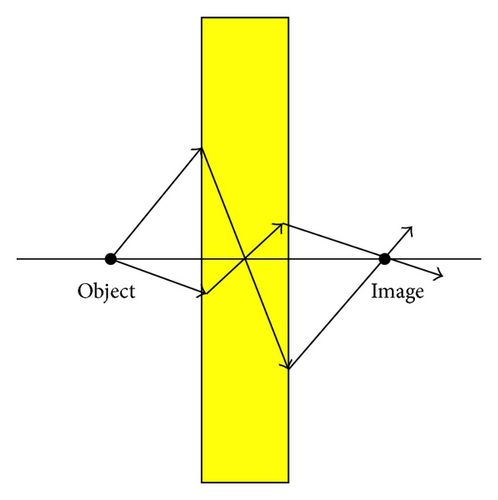
The holes inside the metallic layer are periodically distributed with period η > 0 smaller than the wavelength λ of incident light wave. This layer can be considered as a heterogeneous or perforated media and our goal is to give a physically consistent approach to transmission properties of heterogeneous media using the techniques from homogenization theory and applied analysis. We obtain an effective (upscaled) scaterring problem where the metallic layer with holes is replaced by a homogenized structure with effective permittivity ε_eff and permeability μ_eff. We also obtain the tranmission coefficient T in terms of incident wave number k and incident angle θ. We will see that, for lossless materials with (real) negative permittivity ε_η, perfect transmission T = 1 can be obtained for every θ and suitable value for k. In the recent times, several significant investigations for metamaterials have been done. In [4] the connection between the high transmission and the excitation of surface plasmon polaritons has been established. The photonic band structure of the surface plasmons is evaluated numerically, In [5] the authors have calculated the transmission coefficients for the lamellar gratings, while the effect of surface plasmons on the upper and lower boundary of the layer is investigated in [6]. In [7], the effect of finite conductivity is studied. In [8], the relation between the high transmission effect and the negative index material is obtained with a fishnet like structure. A homogenization method is proposed in [9] where the author accentuates the connection between the skin depth of evanescent modes in the metallaic structure and the period of the gratings. Some results in this direction can be found in [10–13].

Two-scale convergence has proven to be a very efficient tool in homogenization theory while dealing with the problems where the underlying medium is heterogenous. The concept of two-scale convergence is first introduced by Nguetseng in [14]. This convergence criterion and the results related to it have been used extensively in the homogenization of partial differential equations; see Allaire [15, 16], Cioranescu and Donato [17], and Mahato and Böhm [18]. In this work too, we have used the two-scale convergence of an oscillating sequence and its gradient; see Section 1.4. At this point we would like to point out that the geometry of metallic structure in this work is generalized compared to that considered in [3]. In [3] due to the rectangular shapes of the metallic gratings, the coefficients of the effective system were determined by the help of a scalar, one-dimensional shape function given by the hyperbolic functions; however in our work where the considered geometry is more realistic, such nice representation is not possible. To deal with this problem in this work an eigenvalue approach has been proposed and this eigenvalue problem in the unit cell Y helps us to determine the effective parameters of the problem.

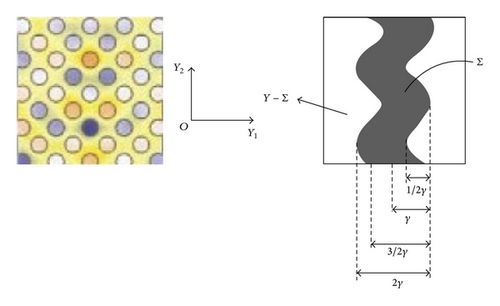
Although this paper can be compared with [3] in some way, the major difference in this work is that our limit function of (see Section 1.5 for details) and the limit function in [3] are totally different. In [3], the authors worked with a rectangular metallic subpart Σ of type (−γ, γ)×(−1/2, 1/2) and therefore by defining a suitable test function, they have shown that the first component of j₀ vanishes and they obtain . This is clearly not the case in this paper as the metallic subpart Σ is chosen to be sinusoidal along y₂-axis due to the geometry of the metallic structure given by Figure 1. This will lead to nonvanishing componenets of j₀ and we end up having a different j₀ compared to that in [3] and hence, we will obtain a different upscaled equation. Also no explicit representation of can be obtained due to the geometry of Σ.

In Sections 1.1, 1.2, and 1.3, we will outline the model in detail. In Section 2, we gather some mathematical tools required to do the analysis and we state our main results. In Sections 3 and 4 we will prove the main results.

1.1. Model

We investigate the time-harmonic solutions of a Maxwell equations with a fixed wave number k and the corresponding wave length λ = 2π/k. Let the metallic structure remain unchanged towards x₃-direction and the metallic field, denoted by , is parellel to x₃; that is, , where .

The heterogenoeus domain Ω has a metallic structure of finite length and finite height in

, and the slits (vacuum) are repeated periodically with a small period η > 0, compare Figure 1. The period η is assumed to be infinitesimally small with respect to the wavelength λ. The relative permittivity of the metal is denoted by ε. Since the permittivity of conductors has large absolute values, we assume that it depends on η and consider ε = ε_η. We obtain nontrivial effects due to plasmonic resonance for |ε_η| ∝ η⁻², compare [3, 13]. If Σ_η denotes the matallic part in Ω, we set

()

where

. Due to ohmic losses inside the metal, Im⁡(ε_η) is always assumed to be positive in a physical system which means we always take Im⁡(ε_r) ≥ 0 and ε_r ≠ 0. A material is called a lossless material if Im⁡(ε_r) = 0. Our particular interest is to study a lossless material with negative relative permittivity; that is, Im⁡(ε_r) = 0 and Re⁡(ε_r) < 0. For such ε_r transverse evanescent modes will be generated in the metal. Since Re⁡(ε_r) < 0 and Im(ε_r) = 0, then from (14) we have

; that is, we can obtain wave like solutions and waves cannot penetrate the metallic grating. These evanescent modes can penetrate only in a region which is given by the skin depth of order η. The evanascent mode is related to a surface plasmon solution (in this case a solution which is nonvanishing in the grating but which has exponential decay in the metal). The main aspect of the current work is to generalize the geometric structure of the metallic slab inside Ω given in [3].

1.2. Geometry

Let η > 0 be a small scale parameter and Ω be the domain under investigation which is bounded in

. Let Y≔(−1/2, 1/2)×(−1/2, 1/2) be the representative unit cell in

and Σ be an open set in Y such that

and Y≔Σ ∪ (Y∖Σ). Let us choose Σ in such a way that it follows a sinusoidal profile along y₂-axis; that is,

()

Keeping physics of the problem in mind, Σ denotes the mettalic part which lies between the two columns of holes in the metallic structure of type introduced in Figure 1.

The relative aperture volume α = 1 − 3γ/2 ∈ (1/4, 1) and relative metal volume is (3/2)γ, where γ ∈ (0, 1/2). We define 2N_η + 1≔2l/2ηγ. We assume that the compact rectangle

contains (2N_η + 1) number of small rectangles of type (nη − ηγ, nη + ηγ) × (−h, 0), that is, of width 2γη and height h, which include the η-scaled versions of the metallic part Σ (cf. Figures 2 and 3), where each Σ is of width (3/2 )γη and height h. The collection of these small η-scaled versions of the metallic part is the metallic domain Σ_η and assume that the two-dimensional heterogeneous metallic structure introduced in Figure 1, denoted by Σ_η and parellel to x₁-axis, is contained in the closure of the set R≔(−l, l)×(−h, 0) ⊂ Ω with

; that is;

()

see Figure 3.

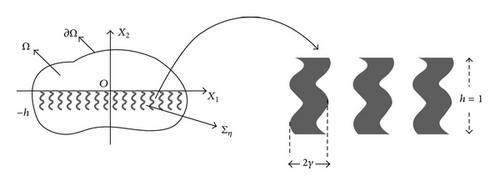
As η → 0, N_η → ∞. Due to nondimensionalization, we are, however, only interested in h = 1.

1.3. Function Spaces

Let θ ∈ [0,1] and 1 ≤ r, s ≤ ∞ be such that 1/r + 1/s = 1. Assume that Ξ ∈ {Ω, Σ_η} and

; then as usual L^r(Ξ) and H^l,r(Ξ) denote the Lebesgue and Sobolev spaces with their usual norms and they are denoted by ‖·‖_r and ‖·‖_l,r. For the sake of clarity if ϕ ∈ L^r(Ξ), then

()

and if ϕ ∈ H^l,r(Ξ), then

()

where

is a multi-index, |α | = α₁ + α₂ + ⋯+α_n, and

. Similarly,

, (·, ·) _θ,r, and [·, ·] _θ are the Hölder, real, and complex interpolation spaces, respectively, endowed with their standard norms; for definition confer [19, 20].

denotes the set of all Y-periodic α-times continuously differentiable functions in y for

. In particular, C_#(Y) is the space of all the Y-periodic continuous function in y. The C^∞-spaces are as usual equipped with their maximum norm whereas the space of all continuous functions C(Ξ) is furnished with supremum norm, compare in [19].

1.4. Two-Scale Convergence

Definition 1. A sequence of functions (u^η) _η>0 in L^r((0, T) × Ω) is said to be two-scale convergent to a limit u ∈ L^r((0, T) × Ω × Y) if

()

for all ϕ ∈ L^s((0, T) × Ω; C_#(Y)).

By ,, and → we denote the two-scale, weak, and strong convergence of a sequence, respectively. Finally, S = (0, T) denotes the time interval.

Lemma 2 (cf. [21]). For every bounded sequence (u^η) _η>0 in L^r(S × Ω) there exists a subsequence (u^η) _η>0 (still denoted by same symbol) and u ∈ L^r((0, T) × Ω × Y) such that .

Lemma 3 (cf. [21]). Let (u^η) _η>0 be strongly convergent to u ∈ L^r((0, T) × Ω), and then , where u₁(t, x, y) = u(t, x).

Lemma 4 (cf. [21]). Let (u^η) _η>0 be a sequence in L^r((0, T); H^1,r(Ω)) such that in L^r((0, T); H^1,r(Ω)). Then and there exists a subsequence (u^η) _η>0, still denoted by same symbol, and such that .

Lemma 5. Let (u^η) _η>0 be a bounded sequence of functions in L^r(S × Ω) such that η∇u^η and η^1/2∇u^η are bounded in L^r(S × Ω)ⁿ. Then there exists some functions such that , , and .

Proof. (i) Since u^η and η∇u^η are bounded sequence of functions in L^r(S × Ω) and L^r(S; L^r(Ω)) ⁿ, respectively, then there exists u ∈ L^r(S × Ω × Y) and U ∈ L^r(S × Ω × Y) ⁿ such that and as η → 0. This means that, for the sequence η∇u^η, we have

()

for all

. We integrate by parts the l.h.s, and which gives

()

And it follows from (7) and (8) that U(t, x, y) = ∇_yu(t, x, y).

(ii) To prove the second part of the lemma, let us choose , where and . Note that the boundedness of η^1/2∇u^η implies the boundedness of η∇u^η in L^r(S × Ω) and hence, by part (i) there exists such that and . Now let us assume that , and then by definition

()

We integrate by parts the l.h.s.; then

()

We compare (9) and (10) which leads us to

()

Since ϕ₁ is independent of y and ∇_y · ϕ₁(t, x) = 0, from (11) it follows that U must be the gradient of some function

such that U(t, x, y) = ∇_yu₁(t, x, y); that is,

. This completes the proof.

1.5. Mathematical Formulation and Statement of the Main Results

We study the Maxwell equations in a complex geometry with highly oscillating permittivities. By η we denote (i) the dimensionless positive scale parameter which represents the small length scale in the geometry

and (ii) the oscillations of large absolute values of the permittivity. We follow the standard nondimenionsalization techniques; for instance, see [3, 18, 22], and so forth and from here on all the quantities considered in this work are dimensionless unless stated otherwise. For the electric field

and magnetic field

, the time-harmonic Maxwell equations are

()

with fixed positive real constants ω, μ₀, and ε₀ denoting the frequency of the incident waves and the permeability and the permittivity of vacuum, respectively. We postulate that all the quantities are x₃-independent and the polarized magnetic field is given by

, where

. By orthogonal property of

and

, we have

. Then (12) reduce to

()

By (13), a straightforward calculation yields

()

where we have set k² = ω²ε₀μ₀. We define the coefficient

which can have a negative real part and that it vanishes in the metal as η → 0. Thus we have the desired Helmholtz equation which we will study in this paper and is given below. We study solutions

()

where the coefficient a_η is given by

()

The set Σ_η ⊂ ⊂R ⊂ Ω describes the complex geometry of the metallic inclusion in Ω; see Figure 3.

Remark 6 (scattering problem). We will investigate the effective behavior of solutions of (15) in two different cases. In the first case we will study an arbitrary bounded sequence of solutions on a bounded domain Ω while the second one concerns the scattering problem. In other words we consider (15) in whole of . For a given incident wave uⁱ, which solves ∇²uⁱ = −k²uⁱ in , we take the Sommerfeld condition as the boundary condition which says that the scattered field satisfies

()

for r = |x | → ∞, uniformly in the angle variable.

Remark 7. Note that for (15) we have not given any boundary conditions; instead we have considered an arbitrary sequence of solutions; however, the uniqueness of solution of the scattering problem will be proven for every η. To state the main results, we rewrite (15) as a system:

()

Comparing with (12), we see that j_η represents (up to a factor and perhaps a rotation) the horizontal electric field

and since the magnetic field

, system (18) is nothing but (12) itself.

Theorem 8 (upscaled equations). Let the matallic geometry be given by Σ_η (Figure 3) on a domain and let the coefficient be as in (16). On we assume that either Im⁡(ε_r) > 0 or ε_r < 0 = Im⁡(ε_r). Let (u_η) _η>0 be the sequence of solutions of (15) such that in L²(Ω) for η → 0. We define U ∈ L²(Ω) as the function

()

where N_w is defined by (36). Then the function ∇U ∈ L²(Ω). The field j_η = a_η∇u_η converges weakly to some j in

which is given by

()

Moreover, the limit functions satisfy the system

()

where

()

By applying Theorem 8 for with a large radius r₀ > 0, we can treat the scattering problem with an incoming wave generated at infinity. We obtain the strong convergence of the scattered field outside the metallic obstacle and we identify the limit U(x) as the solution of the effective diffraction problem. We define the exterior domain outside of R as .

Theorem 9 (effective scattering problem). Let the metallic gratings be given by Σ_η (Figure 1) and the coefficient be as in (16). Assume further that uⁱ is an incident wave solving the free space equation ∇²uⁱ = −k²uⁱ on and u_η is the unique sequence of solutions to (15) such that satisfies (17) and that the solution sequence satisfies the uniform bound

()

Then u_η → U strongly in

with uniform convergence for all derivatives on any compact subset of R^ext. The effective field

is determined as the unique solution of the upscaled equation

()

with (17) for the scattered field (U − uⁱ).

1.5.1. Interface Conditions

The homogenized equation (24) should be understood in the sense of distributions on the whole of . The exterior field for every large radius r; hence its trace on ∂R from outside, denoted by U⁺, is a well-defined element of H^1/2(∂R). Note that as ∇U belongs to L²(B_r), the function U(·, ·) is an element of . This helps us to define traces of U on the horizontal boundary parts from the inside. Moreover, we have the information that the distributional divergence of the vector field j = a_eff∇U is of class .

We define the transmission condition on the boundary ∂R of R with using traces from inside and outside of R. We denote by superscript + (resp., by −) traces from outside (resp., by inside); then problem (24) can be rewritten as

()

with the transmission (interface) conditions

()

where N_w is defined in (36).

2. Derivation of the Effective Model

2.1. A Priori Estimates

Lemma 10. For an with Im(ε_r) > 0, let a_η be defined as in (16). Then there exists a such that

()

where C₀ > 0 is independent of η.

Proof. Let x ∈ Σ_η (if ε_r = a + ib with b > 0, then a_η = η²((a − ib)/(a² + b²))). For an arbitrary small δ > 0, let us define λ≔−1 + δi such that δ|Re(a_η)| ≤ −(1/2)Im⁡(λa_η). There exists a constant C₀ > 0 such that

()

For x ∈ Ω∖Σ_η, we have

()

Lemma 11 (gradient estimate). Suppose that the solution (u_η) _η>0 of (15) is a bounded sequence in L²(Ω); that is, . Then for every compactly contained subdomain Ω^′ ⊂ ⊂Ω, the following estimate holds:

()

where C is independent of the scale parameter η.

Proof. Since , there exists a subdomain Ω^′ ⊂ ⊂Ω such that . Without loss of generality, let us assume that Σ_η ⊂ Ω^′ and take a cut-off function , where Θ(x) = 1 on Ω^′. We test (15) with , where is the complex conjugate of u_η(·). This gives

()

We employ Lemma 10. For a

, we multiply (31) by λ and equate its imaginary part and rearrange the factors of the second integrand which will yield

()

where in the second step we used Young’s inequality. We see that the first integral on the r.h.s. of (32) is bounded by the L²-boundedness assumption on u_η whereas the second integral on the r.h.s. is bounded by the boundedness of |a_η| and

. Using the fact that Θ(x) = 1 on Ω^′, we have

, where C is independent of η and u_η.

2.2. An Eigenvalue Problem in the Unit Cell Y

Let us consider the eigenvalues 0 < λ₁ ≤ λ₂ ≤ ⋯≤λ_n ≤ ⋯ of the problem

()

and we denote {ζ_n} the associated normalized eigenfunctions in

, so that {ζ_n} is an orthonormal basis of L²(Σ). Since

with Im(ε_r) > 0, k²ε_r satisfies the condition

()

We set

()

Let us consider the following boundary value problem:

()

By [23, theorem 8.22], it follows that (i) M_w(y) is a solution of (37) and this solution is unique if k²ε_r ≠ λ_n for all n and (ii) if condition (34) is not fulfilled then (37) has no solution.

In the next theorem we will analyze the behavior of u_η as η → 0 in the sense of two-scale convergence, compare [15]. We notice that the geometry is not only periodic in the x₁-direction but it is also periodic with respect to to the cell Y≔(−1/2, 1/2)×(−1/2, 1/2). The metal part in the cell Y is given by Σ ⊂ Y; see Figure 2.

We recall that the sequnce (u_η) _η>0 is weakly convergent to u ∈ L²(Ω). We define a function u₀(x, y)≔u₀(x₁, x₂, y₁, y₂) as

()

where w(y) is a Y-periodic function defined in (35). We have defined u₀ in such a way that, for every x ∈ Ω, there holds u(x) = ∫_Y u₀(x, y)dy. We will show in next theorem that

as η → 0.

Lemma 12 (two-scale limit). Let (u_η) _η>0, weakly converging to u in L²(Ω), be a sequence of solutions of (15). Then for the function u₀ defined in (38) it holds that .

Outside of R, the strong convergence u_η → u holds in L²(Ω∖R). More precisely, u_η together with all its derivatives converges uniformly on every compact subset .

Proof. We divide the proof into three steps.

(i) From the assumption on u_η and the estimate (30), the sequences (u_η) _η>0 and (η∇u_η) _η>0 are bounded in L²(Ω). Then there exists such that, up to a subsequence, and as η → 0. As a Y-periodic function, u₀ and ∇_yu₀ can be extended by periodicity to all . This shows that which implies that u₀(x, ·) belongs to , in particular, in H¹(Σ) and has a trace on ∂Σ. In other words, does not jump accross ∂Σ by trace theorem (cf. [19, theorem 5.5.1]).

Next, we investigate the coefficient a_η = 1 on the set Ω∖Σ_η. From (30), it follows that which implies strongly in L²(Ω). Since strong convergence implies the two-scale convergence, by localisation Lemma (cf. [3]) the two-scale limit χ₀ vanishes a.e. in R × (Y∖Σ) and in (Ω∖R) × Y. Due to ∇_yu₀ = χ₀, it implies that the function u₀(x, ·) is constant in Y∖Σ and for x ∈ R; and it is constant everywhere for x ∉ R. We use this y-independence to define a function U ∈ L²(Ω) as

()

We note that, at this stage of the proof, u₀ and U are defined as the two-scale limit of u_η and by (39), respectively.

(ii) Characterisation of Two-Scale Limit for x ∈ R. We claim that, for a.e. x ∈ R, the function u₀(x, ·), which belongs to H¹(Σ), solves the linear boundary value problem

()

where (40a), (40b), and (40c) hold in the distributional sense in Σ. To verify this, we choose φ(x, y) = Θ(x)ψ(y), where

and ψ ∈ C^∞(Y; [0,1]) a periodic function on Σ with supp⁡(ψ)∩(Y∖Σ) = ϕ. Using φ_η(x) = φ(x, x/η) as the test function in (15), we obtain

()

Passing the two-scale limit as η → 0

()

Since Θ was chosen arbitrarily, (40a), (40b), and (40c) hold. For every x ∈ R, we write u₀(x, ·) = U(x)(1 + w(·)), where

and w(·) is Y-periodic. Clearly,

satisfies the equation

()

Then, for k²ε_r ≠ λ_n, as shown in Section 2.2, we express w uniquely in terms of the orthonormal basis {ζ_n}. Note that if the condition (34) is violated, the equation in w has no solution and we are led to u₀(x, y) = U(x) = 0.

Therefore, to sum up, we obtain the two-scale limit as

ζ_n(y)∫_Σ ζ_n(y)dy), provided (34) holds. Consequently, for x ∈ R, the weak limit u satisfies

()

Therefore the two-scale limit is given by

()

where

(iii) Strong Convergence Outside of R. We know that u₀(x, y) = u(x) = U(x) holds for a.e. x ∈ Ω∖R and for all y ∈ Y. Moreover, by the assumption on u_η and estimate (30), we have . This then implies that u_η, up to a subsequence, is strongly convergent to U in L²(Ω∖R) by Aubin-Lion’s Lemma, compare [24]. The uniform convergence on compact subsets of u_η and of all its derivatives is a consequence of the fact that u_η Helmholtz equation Δu_η + k²u_η = 0.

With the help of Lemma 12, we can completely determine the two-scale limit of the sequence (u_η) _η>0 if we know the function U(x) which is defined in (39). Now we collect the properties of , its weak limit , and its two-scale limit .

Proposition 13. Let be as in Lemma 12 and U be given by (39). For , we suppose that in . Then is characterized as follows:

(i)
The sequence converges in the sense of two scales to which is given by
()
(ii)
The limit ∇U ∈ L²(Ω) and it holds:
()

Remark 14. We would like to point out a major difference in our j₀ and the limit function j₀ in [3]. In [3], the authors worked with a rectangular metallic subpart Σ of type (−γ, γ)×(−1/2, 1/2) and therefore by defining a suitable test function, they have shown that the first component of j₀ vanishes and they obtain . This is clearly not the case in this paper as the metallic subpart Σ is chosen to be sinusoidal along y₂-axis due to geometry of the metallic structure given by Figure 1. This will lead to nonvanishing componenets of j₀ and we end up having a different j₀ compared to that in [3] and hence, we will obtain a different upscaled equation.

Proof. By (30), it follows that is bounded in which implies that up to a subsequence two-scale converges to some . The weak limit would then be given as .

The Field outside of R. For , . Then by Lemma 12, ∇u_η → ∇U uniformly on compact subsets of . This leads to

()

The Field in the Metal Part of R. We note that |a_η| ≤ Cη² in Σ_η and |a_η| ≤ C in R∖Σ_η; therefore (30) gives and . This implies and by [21, theorem 17], we have a.e. in R × Σ. Moreover, j₀(x, y) = j₀(x) = ∇U(x) for a.e. (x, y) ∈ R × (Y − Σ).

Divergence of j₀. Due to boundedness assumption on u_η, by (18) we have . For and , we test (18) by Θ(x)ψ(x/η) which gives

()

Since

is arbitrary, ∫_Y ∇_yψ(y) · j₀(x, y) dy = 0 for a.e. x ∈ Ω which implies ∇_y · j₀(x, ·) = 0 for y ∈ Y in distributional sense. This shows that

is independent of y; that is,

, some function in x only.

Next we determine the relation between and U as shown in [3]. We define , ψ is Y-periodic, and ψ = 0 in Σ}. We choose a test function φ(x, x/η)≔Θ(x)ψ(x/η), where and ψ ∈ Ξ. We use and ∇·φ(x, x/η)≔∇·(Θ(x)ψ(x/η)) = ψ(x/η)·∇Θ(x) as ∇_y · ψ(y) = 0. Then

()

Since ψ(y)|_Σ = 0 and is nonvanishing in Y∖Σ and by (39) it implies that u₀(x, y) = U(x), all these lead to

()

Therefore, j₀(x, y) = ∇U(x) for

and for reminder j₀(x, y) = 0 for (x, y) ∈ R × Σ.

Proof of (i). To conclude this part, the arguments rely on that of [3]. We consider . We intend to show that for almost every x ∈ R. To show this, we define a function . We notice that (i) ∫_Y j₀(x, y)dy = ∫_Y j(x)dy = j(x) and , (ii) ∇_y · j₀(·, y) = 0 and ∇_y · j₁(·, y) = 0, and (iii) . This implies that (51) holds good for as well as for the conjugate of . Therefore using the fact that from (51), we have

()

Substraction of (52a) and (52b) gives

. Since Θ is arbitrary, therefore ψ₀(y) = 0, which shows that

. This completes the proof of part (i).

Proof of (ii). To verify the claim, let us choose and . Note that . Then from (51), we have

()

It follows that ∇U ∈ L²(Ω) and we find also that

for x ∈ R and

for x ∈ Ω∖R; that is,

, where a(x) = α for x ∈ R and a(x) = 1 for x ∈ Ω∖R.

3. Proofs of Theorems 8 and 9

Proof of Theorem 8. The proof of Theorem 8 is a straightforward consequence of Lemmas 11 and 12 and Proposition 13. It is being shown that if, for any subdomain Ω^′ with R ⊂ Ω^′ ⊂ ⊂Ω, is bounded in L²(Ω^′), then, up to a subsequence, is weakly convergent to some in L²(Ω^′).

By Proposition 13, we have the relation between U and ; that is, the weak and the two-scale limits of are given in terms of U; see (46) and (47). Since Ω^′ is arbitrary, the results of Proposition 13 hold good in all Ω. Now we obatin the limit problem by dividing the proof into two following cases.

Case 1. Let ; then for from (15) we have

()

Case 2. Let x ∈ R; then again for from (15) we have

()

The combination of (54) and (55) gives the limit problem as

()

where

()

Here we can compare our upscaled equation with the limit problem obtained in [3], especially for x ∈ R. Due to their rectangular metallic gratings inside R, the component along x₁ direction vanishes; that is, the first component of and thus the authors obtained their upscaled equation as .

Proof of Theorem 9. The proof is devided into three steps which are demonstrated below.

(i) Uniqueness of the Limit Problem. With a fixed incident field uⁱ we will show that the limit problem (24) has a unique solution. On the contrary, let us assume that U₁ and U₂ are the two solutions of (24) and set u = U₁ − U₂. We consider the equations satisfied by difference of two solutions as

()

We claim that

. The main ingredient for this uniqueness result is Rellich’s first lemma and the fact that a_eff is real and μ_eff has positive imaginary part. In fact a_eff is identity and μ_eff is 1 outside of R. Let us denote the surface of a sphere B_r(0) of radius r by S_r (≔∂B_r(0)), where r is chosen so large such that R ⊂ B_r(0). Let r₀ be such r; then by (59), we have

()

This gives

()

Now we multiply (58) by

and integrate over

. Since (58) holds only in the sense of distributions and due to possible jumps on Γ_hor, we approximate

by smooth functions. By divergence theorem we have

()

The surface integral on r.h.s. of (62) is well defined. This can be argued as follows: outside of R, u is a solution of the Helmholtz equation ∇²u = −k²u and so it is analytic in the exterior of R. Therefore the traces of u and ∂_ru are well defined in

, compare [25]. Comparing the imaginary parts of (62) and investing the knowledge of Im(μ_eff) > 0, then

()

Therefore from (63) we have u = 0 in R. Since r₀ is chosen arbitrarly, for every r from (60) it follows that

()

Thus by Rellich’s first lemma (which states that the solutions u of the Helmholtz equation on an exterior domain satisfying property (64) vanish) we obtain u = 0 in all of which concludes the proof of the uniqueness property, compare [25].

(ii) Convergence to the Limit Problem Assuming an -Bound. Let the radius r₀ > 0 be such that and set . We begin with the assumption that

()

The proof basically follows as the one for Theorem 8. Using (65), up to a subsequence, passing the limit as η → 0, we obtain that

solves (24).

We only need to verify the radiation condition (17). By Lemma 12 it follows that u_η and ∇u_η are uniformly convergent on every compact subset of . Let us choose r < r₀ such that R ⊂ ⊂B_r(0)⊂⊂Ω. By [25, theorem 2.4] and end remark of that theorem, we have from the Sommerfeld radiation condition that the scattered field coincides on with its Helmholtz representation through values and derivatives of u_η − uⁱ on ∂B_r(0). By the similar representation formula, using the values and derivatives of U − uⁱ on ∂B_r(0), we can extend U into all of to a solution of the Helmholtz equation ∇²U = −k²U outside of R. Thus this construction of U shows that U − uⁱ satisfies the Sommerfeld radiation condition. The uniform convergence of u_η → U and ∇u_η → ∇U on ∂B_r(0) implies the uniform convergence of u_η and its derivatives on all compact subsets of exterior of R. Finally by uniqueness of the limit from part (i), as η → 0 for the whole sequence. This shows that the Sommerfeld radiation condition holds for r = |x | → ∞. which establishes (17).

(iii) Boundedness of t_η. In the previous step the limit problem is obtained assuming (65) is true. We will prove that (65) holds true by the method of contradiction. We suppose that t_η → ∞, up to a subsequence, as η → 0. Now we consider the normalized sequence

()

Due to linearity, v_η solves the original scaterring field problem with incident field

as η → ∞. Following the proofs of Lemma 12 and parts (i) and (ii), the function

is the unique solution of (24) and satisfies the Sommerfeld wave condition. By the construction of v_η, we obtain V = 0 and therefore v_η → 0 weakly in L²(Ω).

For outside of R, the gradient estimate (30) for v_η remains valid and hence, v_η|_Ω∖R remains in a bounded subset of H¹(Ω∖R). Then by Rellich compactness lemma as η → 0. For inside of R, we use the estimate (23) on u_η and since t_η → ∞, as η → 0. Therefore as η → 0 but this contradicts the fact that . Thus t_η has to be bounded.

4. Transmission Properties of the Effective Layer

By Theorems 8 and 9 we have obtained the upscaled Helmholtz equation with effective coefficients. In this section we calculate the corresponding effective reflection and transmission properties of the metallic structure.

Let the rectangle R be

for h > 0. We assume planar front of waves that reaches the metallic slab (−h < x₂ < 0) from above (x₂ > 0). The incoming waves would be partially reflected and partially transmitted through the metallic structure. Before we proceed any further we define the following parameters:

M = amplitude of the incident wave, where M = 1
θ≔ incident angle, where θ ∈ (−π/2, π/2)
T≔ complex amplitude and phase shift, where
A_i, B_i≔ complex amplitudes in the structure, where
R≔ complex amplitude of the reflected wave, where

We write the solution U of (24) as

()

where τ≔√(N_w/α). We are yet to determine the coefficients A_i, B_i, R, and T by using the interface (x₂ = 0 and x₂ = −h) and transmission conditions (see (26)).

The Transfer Matrix M. We will calculate a transfer matrix M which basically gives a transformation relation between the solutions on the upper boundary x₂ = 0 and the lower boundary x₂ = −h. To be precise, we define a map

(i.e.,

) as

()

where

is outer normal at x₂ = 0 and x₂ = −h which we choose as (0,1) and (0, −1), respectively. In short the matrix M maps the vector

on the upper boundary to the vector

on the lower boundary. As the map is seen to be linear, M can be expressed as a

matrix. Now we determine the transfer matrix M where the two columns are obtained by M · (1,0) ^t and M · (0,1) ^t.

Columns of M. To obtain the first column of M, we study a solution U of the effective system such that and . The solution U in the interval (−h, 0) is given by (67). By transmission conditions we have , , and . With the help of these conditions, we obtain A₂ = B₂ = 0 and (1/2)A₁B₁cos(τkx₁) = 1 which gives U(x₁, x₂) = cos(τkx₂). With the help of similar transmission condition we obtain

, and

. This gives first column of M as (cos⁡(τkh), ατksin⁡(τkh)) ^t. A similar computation by taking M · (0,1) ^t in account will yield the second column of M as (−(ατk) ⁻¹sin⁡(τkh), cos⁡(τkh)) ^t. Thus the required transfer matrix is given by

()

where τ≔√(N_w/α) and α = 1 − (3/2)γ.

The Transmission Coefficient. After having the matrix M in hand, our next step is to calculate the transfer coefficient T. With the help of matrix M, we map the values

at x₂ = 0+ to the values

at x₂ = −h−; that is,

will get mapped to

. In other words,

()

Here since we are only interested in the transmission coefficient T, we eliminate the unknown R. Now we follow a simple elimination technique shown in [3] and introduce two vectors

and

()

Since the left hand side of (70) is

, multiplying it with v^⊥ will result in the elimination of R from (70). This leads to

()

and a straightforward computation yields

()

By (73), we have determined the transmission coefficient T which depends on wave number k, height of the metallic structure h, the aperture volume α, effective material parameter τ, and the angle θ. We note that τ = √(N_w/α), where N_w is defined by the help of an eigenvalue problem in the metallic part Σ and we also notice that T depends on the wave number k by the relation N_w = N_w(k). For a rather simple N_w, the graph of |T|² against the wave number k is shown in figure 4 in [3].

Let us focus again on the case of a material that permits perfect plasmon waves, that is, of a lossless material with negative permittivity, ε_r < 0; then N_w ∈ (0,1). Also α = 1 − (3/2)γ ∈ (0,1), where 0 < γ < (1/2). This implies that the term ((ατ/cos⁡(θ)) + (cos⁡(θ)/ατ)) in (73) is greater than or equal to 2. Consequently, |T| ≤ 1 and we get |T| = 1⇔cos⁡(τkh) = 1. This corresponds to a resonance of the plasmon waves in the metallic structure (by solving ∇²U = −k²τ²U for x₂ ∈ (−h, 0)) with height h.

We see that this effect can also be deduced from the transfer matrix M of (68), since for cos⁡(τkh) = 1, sin⁡(τkh) = 0 and we get the transfer matrix M = I, the Identity matrix, corresponding to perfect transmission.

Competing Interests

The author declares that they have no competing interests.

Acknowledgments

The author appreciates the financial support provided by Chair of Analysis (at TU Dortmund) during his stay there which made this work possible.

References

1 O′Brien S. and Pendry J. B., Magnetic activity at infrared frequencies in structured metallic photonic crystals, Journal of Physics: Condensed Matter. (2002) 14, no. 25, 6383–6394, https://doi.org/10.1088/0953-8984/14/25/307, 2-s2.0-0036640171.
10.1088/0953-8984/14/25/307
CAS Web of Science® Google Scholar
2 Luo C., Johnson S. G., Joannopoulos J. D., and Pendry J. B., All-angle negative refraction without negative effective index, Physical Review B. (2002) 65, 201104, https://doi.org/10.1103/PhysRevB.65.201104, 2-s2.0-0037095435.
10.1103/PhysRevB.65.201104
CAS Web of Science® Google Scholar
3 Bouchitté G. and Schweizer B., Plasmonic waves allow perfect transmission through sub-wavelength metallic gratings, Networks and Heterogeneous Media. (2013) 8, no. 4, 857–878, https://doi.org/10.3934/nhm.2013.8.857, MR3180689, 2-s2.0-84890191364.
10.3934/nhm.2013.8.857
Web of Science® Google Scholar
4 Porto J. A., García-Vidal F. J., and Pendry J. B., Transmission resonances on metallic gratings with very narrow slits, Physical Review Letters. (1999) 83, no. 14, 2845–2848, https://doi.org/10.1103/PhysRevLett.83.2845, 2-s2.0-3242878340.
10.1103/PhysRevLett.83.2845
CAS Web of Science® Google Scholar
5 Lalanne P., Hugonin J. P., Astilean S., Palamaru M., and Möller K. D., One-mode model and Airy-like formulae for one-dimensional metallic gratings, Journal of Optics A: Pure and Applied Optics. (2000) 2, no. 1, 48–51, https://doi.org/10.1088/1464-4258/2/1/309, 2-s2.0-0033888263.
10.1088/1464-4258/2/1/309
Google Scholar
6 Cao Q. and Lalanne P., Negative role of surface plasmons in the transmission of metallic gratings with very narrow slits, Physical Review Letters. (2002) 88, no. 5, 574031–574034, 2-s2.0-0037017178.
10.1103/PhysRevLett.88.057403
Web of Science® Google Scholar
7 Vallius T., Turunen J., Mansuripur M., and Honkanen S., Transmission through single subwavelength apertures in thin metal films and effects of surface plasmons, Journal of the Optical Society of America A: Optics and Image Science, and Vision. (2004) 21, no. 3, 456–463, 2-s2.0-1542275418.
10.1364/JOSAA.21.000456
Google Scholar
8 Mary A., Rodrigo S. G., Martín-Moreno L., and García-Vidal F. J., Holey metal films: from extraordinary transmission to negative-index behavior, Physical Review B. (2009) 80, no. 16, 8, 165431, https://doi.org/10.1103/PhysRevB.80.165431.
10.1103/PhysRevB.80.165431
Web of Science® Google Scholar
9 Felbacq D., Noncommuting limits in homogenization theory of electromagnetic crystals, Journal of Mathematical Physics. (2002) 43, no. 1, 52–55, https://doi.org/10.1063/1.1418013, MR1872485, 2-s2.0-0035981932.
10.1063/1.1418013
CAS Web of Science® Google Scholar
10 Bouchitté G. and Bourel C., Multiscale nanorod metamaterials and realizable permittivity tensors, Communications in Computational Physics. (2012) 11, no. 2, 489–507, https://doi.org/10.4208/cicp.171209.110810s, MR2850907, 2-s2.0-84055184798.
10.4208/cicp.171209.110810s
Web of Science® Google Scholar
11 Felbacq D. and Bouchitté G., Negative refraction in periodic and random photonic crystals, New Journal of Physics. (2005) 7, article 159, https://doi.org/10.1088/1367-2630/7/1/159, 2-s2.0-24044433946.
10.1088/1367-2630/7/1/159
Web of Science® Google Scholar
12 Bouchitté G. and Felbacq D., Homogenization near resonances and artificial magnetism from dielectrics, Comptes Rendus Mathematique. (2004) 339, no. 5, 377–382, https://doi.org/10.1016/j.crma.2004.06.018, MR2092467.
10.1016/j.crma.2004.06.018
Web of Science® Google Scholar
13 Bouchitté G., Bourel C., and Felbacq D., Homogenization of the 3D Maxwell system near resonances and artificial magnetism, Comptes Rendus Mathematique. (2009) 347, no. 9-10, 571–576, https://doi.org/10.1016/j.crma.2009.02.027.
10.1016/j.crma.2009.02.027
Web of Science® Google Scholar
14 Nguetseng G., A general convergence result for a functional related to the theory of homogenization, SIAM Journal on Mathematical Analysis. (1989) 20, no. 3, 608–623, https://doi.org/10.1137/0520043, MR990867, ZBL0688.35007.
10.1137/0520043
Web of Science® Google Scholar
15 Allaire G., Homogenization and two scale convergence, SIAM Journal on Mathematical Analysis. (1992) 23, no. 6, 1482–1518, https://doi.org/10.1137/0523084.
10.1137/0523084
Web of Science® Google Scholar
16 Allaire G., Two-Scale Convergence and Homogenization of Periodic Structures, 1993, School on Homogenization, Trieste, Italy.
Google Scholar
17 Cioranescu D. and Donato P., An Introduction to the Homogenization, 1999, Oxford University Press.
10.1093/oso/9780198565543.001.0001
Google Scholar
18 Mahato H. S. and Böhm M., Homogenization of a system of semilinear diffusion-reaction equations in an H^1,p setting, Electronic Journal of Differential Equations. (2013) 210, 1–22.
Google Scholar
19 Evans L. C., Partial Differential Equations, 1998, AMS Publications.
10.1090/gsm/019
Google Scholar
20 Lunardi A., Analytic Semigroups and Optimal Regularity in Parabolic Problems, 1995, Birkhäuser, Basel, Switzerland, https://doi.org/10.1007/978-3-0348-9234-6, MR1329547.
Google Scholar
21 Lukkassen D., Nguetseng G., and Wall P., Two scale convergence, International Journal of Pure and Applied Mathematics. (2002) 2, no. 1, 35–86.
Google Scholar
22 Peter M. A. and Böhm M., Different choices of scaling in homogenization of diffusion and interfacial exchange in a porous medium, Mathematical Methods in the Applied Sciences. (2008) 31, no. 11, 1257–1282, https://doi.org/10.1002/mma.966, MR2431426, 2-s2.0-47749091609.
10.1002/mma.966
Web of Science® Google Scholar
23 Renardy M. and Rogers R. C., An Introduction to Partial Differential Equations, 1993, Springer, New York, NY, USA, MR1211418.
Google Scholar
24 Simon J., Compact sets in the space L^p (O,T; B), Annali di Matematica Pura ed Applicata. (1986) 146, no. 1, 65–96, https://doi.org/10.1007/BF01762360.
10.1007/BF01762360
Web of Science® Google Scholar
25 Colton D. and Kress R., Inverse Acoustic and Electromagnetic Scattering Theory, 1998, 93, Springer, Berlin, Germany.
10.1007/978-3-662-03537-5
Google Scholar

All articles

Upscaling of Helmholtz Equation Originating in Transmission through Metallic Gratings in Metamaterials

Abstract

1. Introduction

1.1. Model

1.2. Geometry

1.3. Function Spaces

1.4. Two-Scale Convergence

1.5. Mathematical Formulation and Statement of the Main Results

1.5.1. Interface Conditions

2. Derivation of the Effective Model

2.1. A Priori Estimates

2.2. An Eigenvalue Problem in the Unit Cell Y

3. Proofs of Theorems 8 and 9

4. Transmission Properties of the Effective Layer

Competing Interests

Acknowledgments

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Upscaling of Helmholtz Equation Originating in Transmission through Metallic Gratings in Metamaterials

Abstract

1. Introduction

1.1. Model

1.2. Geometry

1.3. Function Spaces

1.4. Two-Scale Convergence

1.5. Mathematical Formulation and Statement of the Main Results

1.5.1. Interface Conditions

2. Derivation of the Effective Model

2.1. A Priori Estimates

2.2. An Eigenvalue Problem in the Unit Cell Y

3. Proofs of Theorems 8 and 9

4. Transmission Properties of the Effective Layer

Competing Interests

Acknowledgments

References

Figures

References

Related

Information