Physics Research International
Volume 2016, Issue 1 6761372
Research Article
Open Access

Vibration Analysis of Euler-Bernoulli Beams Partially Immersed in a Viscous Fluid

Wafik Abassi, 

Wafik Abassi

Arts et Métiers ParisTech, ENSAM Angers, 2 boulevard du Ronceray, 49035 Angers, France ensam.eu

Search for more papers by this author
Adil El Baroudi, 

Corresponding Author

Adil El Baroudi

Arts et Métiers ParisTech, ENSAM Angers, 2 boulevard du Ronceray, 49035 Angers, France ensam.eu

Search for more papers by this author
Fulgence Razafimahery, 

Fulgence Razafimahery

IRMAR, Université de Rennes 1, Campus de Beaulieu, 35042 Rennes Cedex, France univ-rennes1.fr

Search for more papers by this author
First published: 21 February 2016
https://doi.org/10.1155/2016/6761372
Citations: 2
Academic Editor: Israel Felner

Abstract

The vibrational characteristics of a microbeam are well known to strongly depend on the fluid in which the beam is immersed. In this paper, we present a detailed theoretical study of the modal analysis of microbeams partially immersed in a viscous fluid. A fixed-free microbeam vibrating in a viscous fluid is modeled using the Euler-Bernoulli equation for the beams. The unsteady Stokes equations are solved using a Helmholtz decomposition technique in a two-dimensional plane containing the microbeams cross sections. The symbolic software Mathematica is used in order to find the coupled vibration frequencies of beams with two portions. The frequency equation is deduced and analytically solved. The finite element method using Comsol Multiphysics software results is compared with present method for validation and an acceptable match between them was obtained. In the eigenanalysis, the frequency equation is generated by satisfying all boundary conditions. It is shown that the present formulation is an appropriate and new approach to tackle the problem with good accuracy.

1. Introduction

The objective of this paper is to provide an analytical method to calculate the coupled frequencies of vibration of microbeams partially immersed in a viscous fluid. The microbeams are clamped on one edge while the other edge is free.

The motivation of this work is to provide a theoretical model that can be used in the design and interpretation of density and viscosity sensors.

Due to their size and potential for highly sensitive and low cost compact device applications, microstructures are becoming increasingly attractive for sensing applications and have been studied extensively in recent years. Microstructures are commonly used in atomic force microscopy (AFM) to probe surface properties and to measure interfacial forces [1–7], in biological and chemical sensors [8–10]. A precise modeling of the solid-fluid interaction and the determination of the frequency response enable the measurement of the density and the rheological behavior of fluids [11–16]. Reference [16] uses finite element analysis (FEA) method in order to predict the dynamic response of the cantilever beam. This method can be easily applied to the measurement of the fluid viscosity.

For microstructures, fluid viscosity can greatly affect their frequency response. Reference [7] presented a rigorous theoretical model for the frequency response of cantilever beams that are undergoing flexural vibrations and immersed in viscous fluids, which is of particular relevance to applications of the AFM. The knowledge and understanding of the frequency analysis of microbeams are of fundamental practical importance in application to the AFM.

The frequency analysis of a microbeam can be dramatically affected by the properties of the fluid in which it is immersed. Whereas calculation of the natural frequencies in vacuum can be performed routinely, analysis of the effects of immersion in fluid poses a formidable challenge. The modal response of an immersed microbeam can be considerably affected by the properties of fluid. The added mass effect due to the fluid structure interaction can, however, cause considerable variations in natural frequencies. The knowledge and understanding of this viscous fluid-structure coupling are lacking at present.

In this contribution, we investigate the vibrational behavior of microbeams partially immersed in a viscous fluid, which describes the interrelation between the fluid’s density and viscosity. For a viscous fluid problem, the analytical formulation is based upon a convenient decomposition of the velocity field into two contributions, one being related to the scalar potential and the other being the vector potential. The solutions of the differential equations of motion turn out to be complex and can be conveniently treated with the aid of the symbolic software Mathematica. Furthermore, this work investigates the influence of the fluid’s viscosity on the vibrational behavior of the microbeams.

2. Modal Analysis of Beams and Frequency Equation

Modal analysis of elastic immersed structures is needed in every modern construction and should have wide engineering application. In this study, modal analysis is important to predict the dynamic behavior of the submerged beams. It is well known that the natural frequencies of the submerged elastic structures are different from those in vacuum. The effect of fluid forces on the immersed beam decreases the natural frequencies from those that would be measured in the vacuum. This decrease in the natural frequencies is caused by the increase of the kinetic energy of the fluid-beams system without a corresponding increase in strain energy. The Euler-Bernoulli beam is partially immersed inside rectangular fluid domain (Figure 1). Consider a beam of length 3.06·10−2 [m], width 4.6·10−3 [m], and thickness 1.27·10−4 [m] as shown in Figure 1, which corresponds to a model developed in [16]. The interaction between the fluid and the Euler-Bernoulli beams is taken into account to calculate the natural frequencies and mode shapes of the coupled system. The dynamics of each beam portion are treated separately. It is assumed that the beam has aligned neutral axis.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Sketch of beam composed of 2 uniform beam segments (denoted by (1) and (2)) partially immersed in a fluid-filled rectangular geometry.

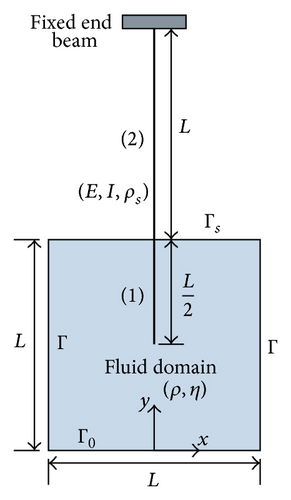
2.1. Mathematical Formulation

In this section we present the general theory for the dynamic deflection of beams partially submerged in a viscous fluid. A schematic depiction of beams partially submerged in viscous fluid is displayed in Figure 1. We begin by discussing some general assumptions and approximations taken into account in the present theoretical model. It is assumed that the cross section of the beams is uniform over its entire length and the length of the beams greatly exceeds its width. Also the beams are an isotropic linearly elastic solid and internal frictional effects are negligible. The amplitude of the vibrations of the beams is small. In addition, we shall neglect all torsional effects in the beams and only consider the flexural modes of vibration and we shall consider modes whose motion is strict in the x-direction. For beams vibrating at small amplitudes (small compared to the beams dimensions), the governing dynamical equations ignoring shear deformation and rotary inertia effects for the transverse deflection ui(y, t) (i = 1 for submerged portion and i = 2 for portion in vacuum) of uniform elastic beams can be written in the form
()
()
where u1(y, t) and u2(y, t) are the lateral deflections at distance y (spatial coordinate) along the length of the beams and t is time; EI, ρs, and S are the flexural rigidity, the mass per unit volume, and the cross-sectional area of the beam, respectively. ffluid is the external force per unit length acting on the beam in the direction of the flexural displacement, which is caused by the viscous fluid in the beams. The dynamics of each beam portion are treated separately.
For a beam moving in a viscous fluid, the applied load ffluid can be obtained by integrating the normal component of the total force exerted by the fluid over the beam section. To proceed with the analysis, the general form of ffluid is required. We therefore examine the equations of motion for the fluid. For this, the viscous fluid mode shapes are first computed for the square domain fluid assuming the boundary conditions given in Figure 1. From conservations of mass and momentum, the motion of the fluid is governed by (see [17])
()
()
in which is the fluid velocity vector, ρ is the density of the fluid, and σ is the total fluid stress tensor (pressure and viscous forces). Since the amplitude of vibration of each beam is small compared to its cross-sectional dimensions, it then follows that all nonlinear convective inertial effects in the fluid can be neglected, and the hydrodynamic loading on the beam will be a linear function of its displacement. This implies that the fluid dynamics can be modeled as an unsteady linear Stokes flow. Assuming that the fluid is Newtonian, its constitutive equation is given by
()
where I is a unit tensor, η is the dynamic viscosity, and p is the fluid pressure. The boundary conditions which define the fluid domain are
()
()
()
The equations of motion (3) and (4) are highly complex and coupled. However, a simpler set of equations can be obtained by introducing scalar potentials ϕ and ψ, known as the Helmholtz decomposition [18] in a way which permits easily transferring the vector problem formulation ((3) and (4)) to scalar problem formulation. In flow fields, the velocity is thereby decomposed into a potential flow and a viscous flow. In other words, the velocity v can be expressed as a sum of the gradient of a scalar potential ϕ and the curl of a vector potential Ψ as follows [18]:
()
where Ψ is a vector stream function. Using the problem symmetry, the vector potential Ψ reduces to a scalar equation; that is, Ψ = (0,0, ψ), using the condition ∇·Ψ = 0, and substituting the above resolutions into (3) and (4), after some manipulations, the equation for the conservation of mass (3) becomes the Laplace equation
()
and the equation for the conservation of momentum (4) becomes
()
where ν is the kinematic fluid viscosity and ∇2 = ∂2/∂x2 + ∂2/∂y2 is the Laplacian operator. Thus, the Stokes equation is reduced to formulation (10) and (11). Moreover, adopting the Cartesian coordinate system (x, y) and using expression (9), the velocity components, v = (vx, vy), may be expressed as simple functions of compressional and shear wave potentials in the form
()
and the pertinent stress-velocity relations are
()

2.1.1. Field Expansions

Consider time harmonic motion throughout with angular frequency ω and with the exp(iωt) dependence suppressed for simplicity. Applying the classical technique of separation of variables in the Cartesian coordinates, the solution of (10) and (11) after some manipulations, and taking into account boundary condition (6) can be shown to be
()
()
()
with the complex-valued coefficients
()
where β = nπ/L and n is an integer. A, B, C, and D are unknown coefficients which will be determined later by imposing the appropriate boundary conditions. Hence, the fluid particle velocity field can be determined from (12) in the form
()
()
Consequently, direct substitution of the expansions (14)–(19) into the stress-velocity relations (13), after some manipulations, leads to
()
()
()
In order to determine the unknown constants, the appropriate boundary conditions (7) and (8) must be explicitly used. Substituting the total fluid stress tensor components (20)–(22) into boundary conditions equations (8) and velocity components (18)-(19) into boundary conditions equations (7), and after some considerable algebraic manipulation, the scalar potentials ϕ and ψ become
()
()
where
()
Using the expressions of ψ and ϕ from (23) and (24), in (12), we have the following expressions for the velocity components:
()
()
Components of the stress tensor can be obtained by substituting the expressions of velocity components vx; vy, from (26) and (27), and the expression of scalar potential ϕ from (24) in (13) which comes out as
()
()
()
Now we can integrate the normal component of the total force exerted by the fluid over the beam section in order to obtain the external force per unit length acting on the beam in the direction of the flexural displacement ffluid. Hence, the deflection of the immersed part of the beam (which is equal to u1(y, t) = u1(y)exp⁡ (jωt)) can be determined from (1) and (28) in the form
()
where primes denote differentiation with respect to the position variable y.

2.2. Method of Solution and Frequency Equation

The general solutions of the ordinary differential equations (31) and (2) for the beams system, as shown in Figure 1, can be written in different segments in terms of trigonometric functions and represent propagating waves and hyperbolic functions represent evanescent waves as
()
()
where Ω is the flexural wavenumber and is given by
()
Equation (32) shows that the parameters
()
are resonance frequency parameters and can be plotted for different values of n.
The nine constants A1, B1, C1, D1, A2, B2, C2, D2, and A can be found by imposing the following boundary conditions. Equations (32) and (33) are the general solution for the vibration modes of beams partially immersed in fluid. In the case of a coupled system, the effect of fluid viscosity on the flexible beams must be considered. On the fluid-beams interface, the normal velocity must be continuous. Therefore, the fluid velocity and the deflection of a beam u1 satisfy the relation
()
Substituting (26) and (32) into (36), and after some manipulations, leads to the following equation:
()
Both sides of (37) are integrated over L/2 < y < L to yield the following equation:
()
where Υ and the coefficients I1, I2, I3, and I4 are written down explicitly in Appendix E. Now the expression of the lateral movement of the submerged beams in contact with the fluid u1 can be formulated using (32) and taking into account (38) as
()
where
()
Now, to derive the frequency equation of beams partially immersed in fluid, one assumes that, on the interface between each portion of the beam at the position y = L, the deflection, the rotation angle, the internal shear force, and bending moment of the beam must be continuous. This is satisfied when
()
To complete the formulation of the boundary-value problem, the four boundary conditions for the beam ends (y = L/2 = a and y = 2L = b) considered in this work are specified as follows:
()
Combining the boundary conditions ((41) and (42)) with (33) and (39) yields the following linear homogeneous system of eight equations:
()
where M is a 8 × 8 matrix whose elements are designated as Mij. This system can have nontrivial solutions only if the determinant of the matrix M is zero, leading to the frequency equation. The matrix M is written down explicitly in Appendix F.

3. Analytical and Numerical Results and Validation

The model that was developed in Section 2 can be validated by comparing the analytical results to model results calculated using Comsol Multiphysics FEM Simulation Software. This comparison used beams with Young’s modulus being E = 200·109 [Pa], Poisson’s ratio being ν = 0.3, and density being ρ = 9450 [kg/m3]. The fluid used in the rectangular container for which density of 965 [kg·m−3] and dynamic’s viscosity of 0.1 [Pa·s] is assumed.

For coupled vibration analysis of beams partially immersed in a viscous fluid, the accuracy of the present method has been compared with the results obtained with Comsol Multiphysics FEM Simulation Software. The FEM used model had 585039 number of degrees of freedom and was analyzed using the algorithm based on the UMFPACK method [19].

In this paper the comparison of the values of the angular frequency parameter ω is given in Table 1. As one can see from the comparison, very good agreement with those of FEM is obtained.

Table 1. The first 24 coupled natural angular frequencies ω of the partially immersed beams in a viscous fluid. Comparison of frequency between FEM and present method.
Order Present FEM Difference (%)
1 4.90 4.86 0.82
2 18.18 17.91 1.50
3 20.26 20.01 1.24
4 21.11 20.86 1.19
5 24.68 24.50 0.73
6 30.48 30.20 0.92
7 31.59 31.44 0.47
8 39.24 38.91 0.84
9 44.68 44.51 0.38
10 47.65 47.31 0.71
11 50.20 49.72 0.96
12 54.68 54.02 1.22
13 56.10 55.33 1.39
14 61.47 61.25 0.35
15 61.90 61.36 0.88
16 64.57 64.15 0.65
17 67.29 66.72 0.85
18 73.47 72.99 0.65
19 79.63 79.21 0.53
20 80.06 79.42 0.80
21 85.67 85.41 0.30
22 87.58 87.09 0.56
23 91.33 90.85 0.52
24 97.44 97.10 0.35

With the derived eigenfrequency equations, natural frequencies ω are calculated in the software Mathematica. To validate the analytical results, the natural frequencies and mode shapes are also computed using Comsol Multiphysics FEM Simulation Software. The natural frequencies are computed directly from determinant of (43).

Table 1 shows the comparison of the first 24 natural frequencies and the corresponding mode shapes of viscous fluid by FEM and the present method (43). The good agreement is observed between the results of the present method and those of FEM and the relative difference (100 × (Present − FEM)/FEM) is ⩽2%. This shows that the algorithm implemented in Comsol Multiphysics [20] software for numerical computation is highly reliable and accurate. Mesh refinement can significantly decrease the relative difference.

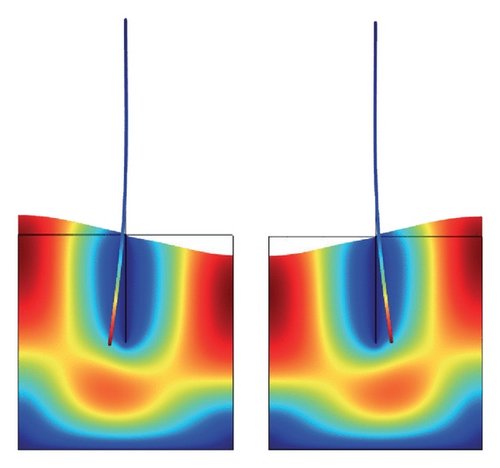
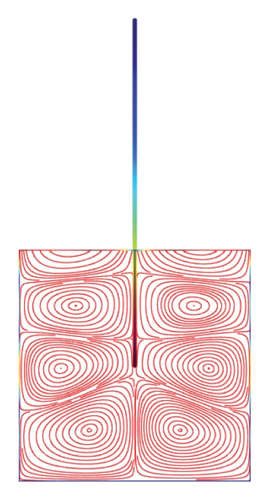
The two possible first coupled mode shapes are represented in Figure 2. A very good agreement with Figure  3 of [16] confirms the adequate implementation of the method in the FEM software.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Two possible first coupled mode shapes.

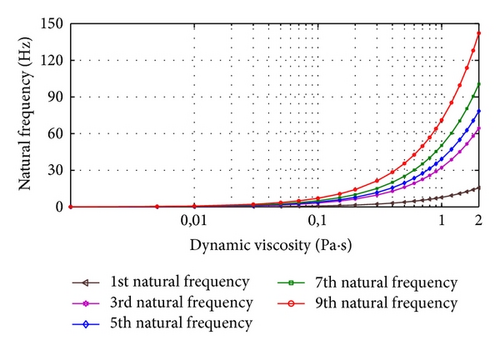
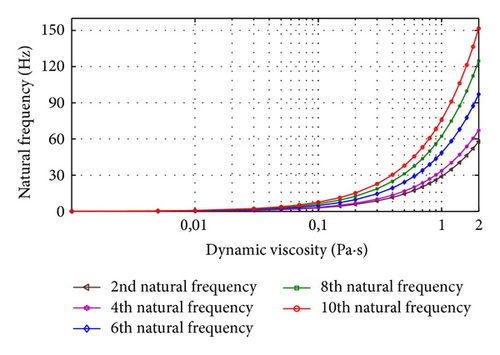
Figures 3 and 4 show the influence of fluid’s viscosity on the odd and even natural frequencies. It is seen that the effect of viscosity is very interesting and decreases the frequency of beams. These figures show also for small fluid’s viscosity that the model is not suitable to describe properly the vibrational behavior of beams immersed in a viscous fluid. In this case, the most appropriate model is the model developed in [21]. In other words, the viscosity terms can be neglected and the resulting model is called inertial coupling [22].

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
The influence of fluid’s viscosity on the first five odd natural frequencies.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
The influence of fluid’s viscosity on the first five even natural frequencies.

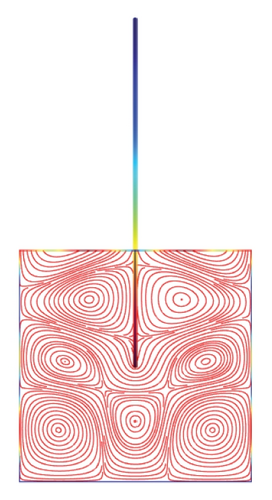
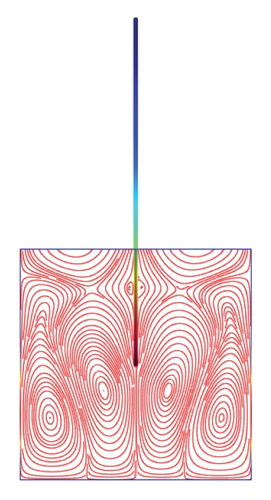
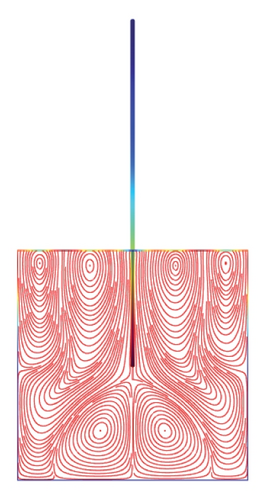
Figures 5(a)–5(f)–8(a)–8(f) obtained by Comsol show the first 24 coupled modal shapes with the corresponding eigenvalues ω. In these figures, solid lines denote streamlines (i.e., Stokes eddies) caused by system boundaries and fluid structure interaction. In addition, the formation of Stokes eddies is not affected by the presence of an obstacle (beam) in the fluid domain. As expected these Stokes eddies increase when the angular frequency is raised like in the case without obstacle. Finally, these Stokes eddies are symmetric with respect to the obstacle.

Details are in the caption following the image
Figure 5 (a) Mode 1
Open in figure viewerPowerPoint
View of displacement filled of beams and Stokes eddies, showing various mode shapes for the coupled vibration.
Details are in the caption following the image
Figure 5 (b) Mode 2
Open in figure viewerPowerPoint
View of displacement filled of beams and Stokes eddies, showing various mode shapes for the coupled vibration.
Details are in the caption following the image
Figure 5 (c) Mode 3
Open in figure viewerPowerPoint
View of displacement filled of beams and Stokes eddies, showing various mode shapes for the coupled vibration.
Details are in the caption following the image
Figure 5 (d) Mode 4
Open in figure viewerPowerPoint
View of displacement filled of beams and Stokes eddies, showing various mode shapes for the coupled vibration.
Details are in the caption following the image
Figure 5 (e) Mode 5
Open in figure viewerPowerPoint
View of displacement filled of beams and Stokes eddies, showing various mode shapes for the coupled vibration.
Details are in the caption following the image
Figure 5 (f) Mode 6
Open in figure viewerPowerPoint
View of displacement filled of beams and Stokes eddies, showing various mode shapes for the coupled vibration.
Details are in the caption following the image
Figure 6 (a) Mode 7
Open in figure viewerPowerPoint
View of displacement filled of beams and Stokes eddies, showing various mode shapes for the coupled vibration.
Details are in the caption following the image
Figure 6 (b) Mode 8
Open in figure viewerPowerPoint
View of displacement filled of beams and Stokes eddies, showing various mode shapes for the coupled vibration.
Details are in the caption following the image
Figure 6 (c) Mode 9
Open in figure viewerPowerPoint
View of displacement filled of beams and Stokes eddies, showing various mode shapes for the coupled vibration.
Details are in the caption following the image
Figure 6 (d) Mode 10
Open in figure viewerPowerPoint
View of displacement filled of beams and Stokes eddies, showing various mode shapes for the coupled vibration.
Details are in the caption following the image
Figure 6 (e) Mode 11
Open in figure viewerPowerPoint
View of displacement filled of beams and Stokes eddies, showing various mode shapes for the coupled vibration.
Details are in the caption following the image
Figure 6 (f) Mode 12
Open in figure viewerPowerPoint
View of displacement filled of beams and Stokes eddies, showing various mode shapes for the coupled vibration.
Details are in the caption following the image
Figure 7 (a) Mode 13
Open in figure viewerPowerPoint
View of displacement filled of beams and Stokes eddies, showing various mode shapes for the coupled vibration.
Details are in the caption following the image
Figure 7 (b) Mode 14
Open in figure viewerPowerPoint
View of displacement filled of beams and Stokes eddies, showing various mode shapes for the coupled vibration.
Details are in the caption following the image
Figure 7 (c) Mode 15
Open in figure viewerPowerPoint
View of displacement filled of beams and Stokes eddies, showing various mode shapes for the coupled vibration.
Details are in the caption following the image
Figure 7 (d) Mode 16
Open in figure viewerPowerPoint
View of displacement filled of beams and Stokes eddies, showing various mode shapes for the coupled vibration.
Details are in the caption following the image
Figure 7 (e) Mode 17
Open in figure viewerPowerPoint
View of displacement filled of beams and Stokes eddies, showing various mode shapes for the coupled vibration.
Details are in the caption following the image
Figure 7 (f) Mode 18
Open in figure viewerPowerPoint
View of displacement filled of beams and Stokes eddies, showing various mode shapes for the coupled vibration.
Details are in the caption following the image
Figure 8 (a) Mode 19
Open in figure viewerPowerPoint
View of displacement filled of beams and Stokes eddies, showing various mode shapes for the coupled vibration.
Details are in the caption following the image
Figure 8 (b) Mode 20
Open in figure viewerPowerPoint
View of displacement filled of beams and Stokes eddies, showing various mode shapes for the coupled vibration.
Details are in the caption following the image
Figure 8 (c) Mode 21
Open in figure viewerPowerPoint
View of displacement filled of beams and Stokes eddies, showing various mode shapes for the coupled vibration.
Details are in the caption following the image
Figure 8 (d) Mode 22
Open in figure viewerPowerPoint
View of displacement filled of beams and Stokes eddies, showing various mode shapes for the coupled vibration.
Details are in the caption following the image
Figure 8 (e) Mode 23
Open in figure viewerPowerPoint
View of displacement filled of beams and Stokes eddies, showing various mode shapes for the coupled vibration.
Details are in the caption following the image
Figure 8 (f) Mode 24
Open in figure viewerPowerPoint
View of displacement filled of beams and Stokes eddies, showing various mode shapes for the coupled vibration.

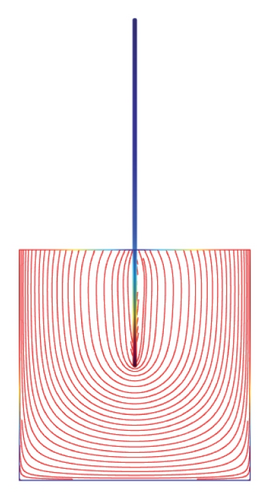
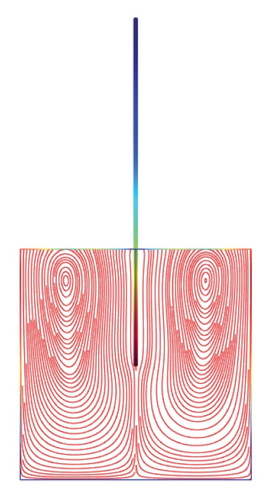
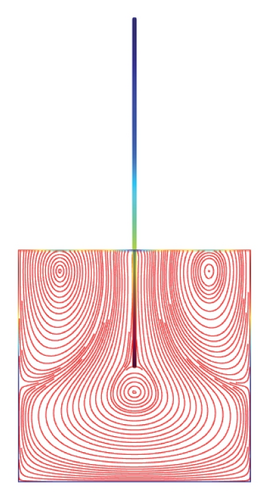
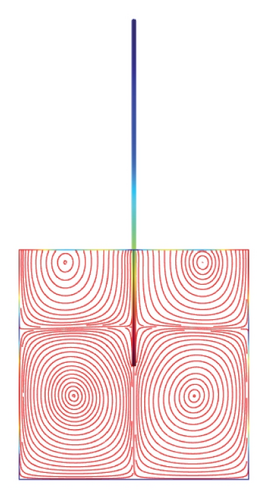
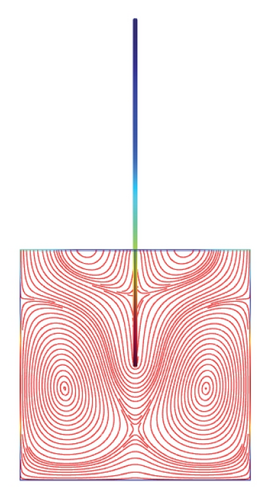
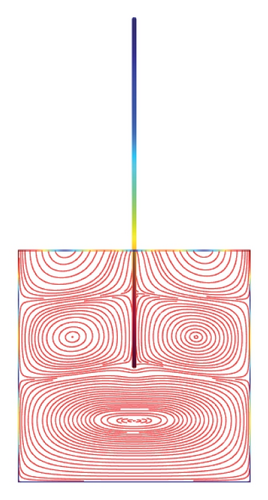
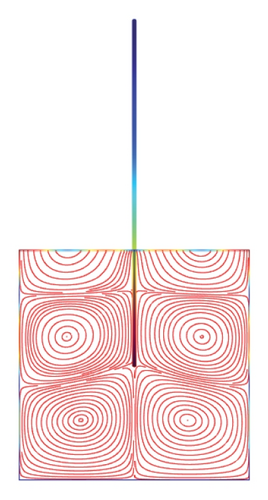
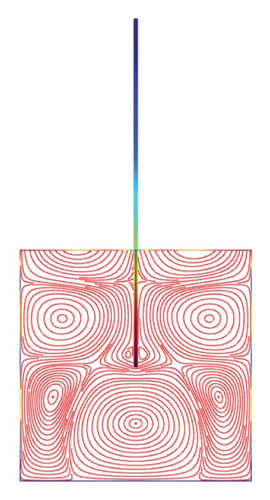
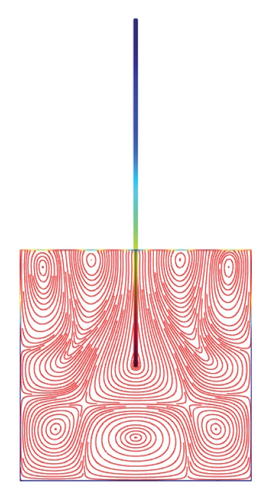
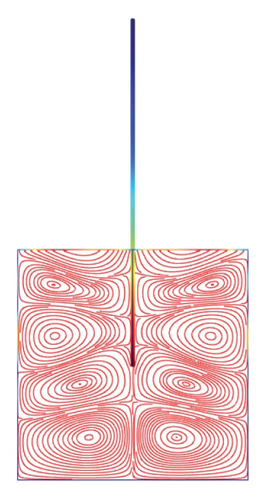
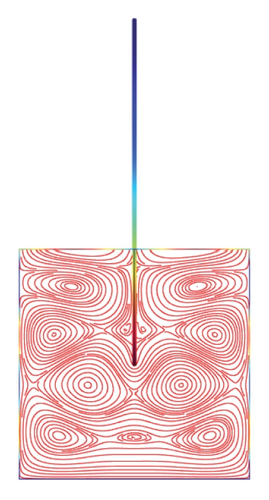
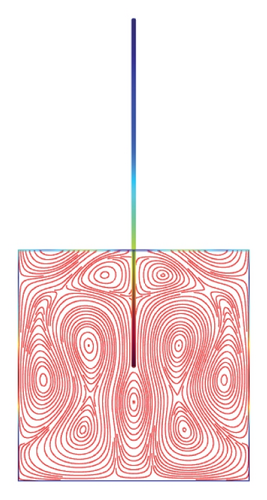
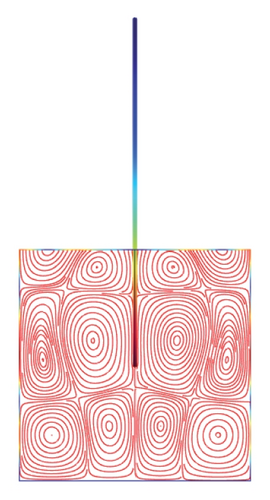
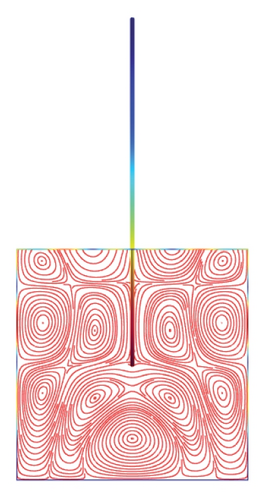
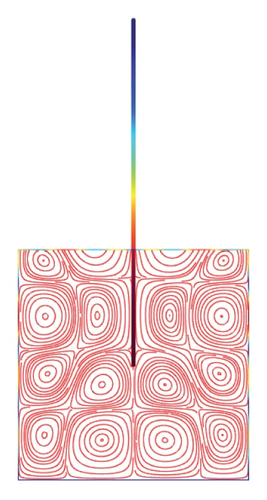
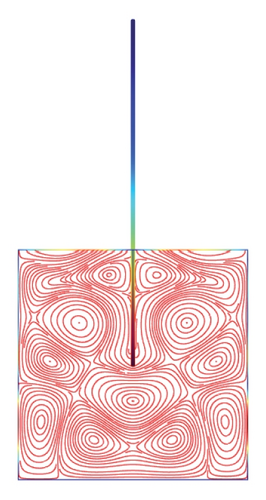
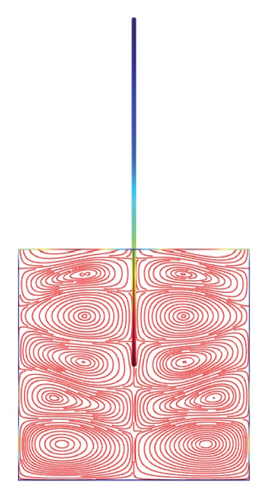
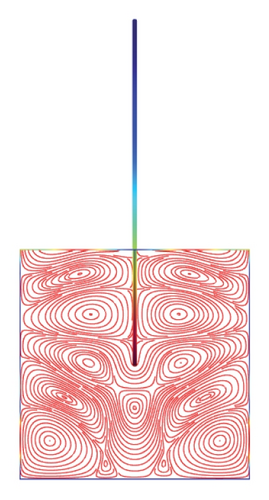
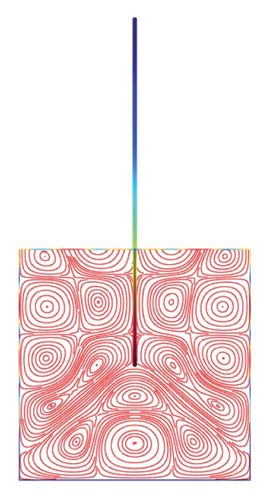
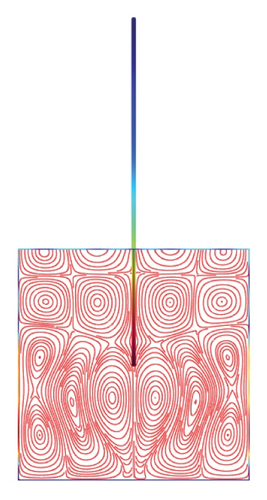
4. Conclusion

This paper has presented an analytical method to understand the modal behavior of beams partially immersed in a viscous fluid. The validity of the present solution is solidly confirmed numerically. The main application of the proposed method is in characterization of rheological properties of viscous materials [16]. In addition the study can be also extended further for the optimization tool for complex engineering design problems.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Appendices

A. Analytical Expression for the Scalar Potentials

(i) Solution of (11). A time harmonic dependence exp⁡ (jωt) is assumed, with j being the imaginary unit, ω being the circular frequency, and t  being the time. We introduce a new auxiliary variable α defined as . The first of the two subequations (Equation (11)) consists of determining the scalar potential ψ(x, y) satisfying the homogeneous diffusion equation
()
By separation of variables, the scalar potential ψ(x, y) can be written as
()
where ψx(x) and ψy(y) are given by the following ordinary differential equation:
()
The linear independent solutions of these equation yield a general pressure field of the form
()
where a1, a2, a3, and a4 are unknown coefficients which will be determined later by imposing the appropriate boundary conditions.
(ii) Solution of (10). In a similar manner, the solution of (10) can be defined. The solution consists of determining the scalar potential ϕ(x, y) satisfying the Laplace equation
()
By separation of variables, after some elementary manipulations, the linear solution of these equations yields a general scalar potential ϕ(x, y) of the form
()
(iii) Boundary Conditions. The boundary condition equation (6) can be expressed by
()
Substituting ϕ(x, y) and ψ(x, y) into boundary condition above gives the analytical solution for potential function (14) and (15). Now using the second equation of (11), the pressure can be presented by (16).

B. No-Slip Condition and Stress-Free Boundary Condition

In this paper the interface Γ0 (7) is assumed to be rigid, leading to
()
Substituting (18) and (19) into above rigid boundary equations gives
()
The interface Γs (8) is assumed to be free boundary stress, leading to
()
Substituting (21) and (22) into above free boundary stress equations gives the first conditions, for example,
()
Note that, from the above equation, we can obtain
()
By replacing the constants into (14) and (15), the potential functions ϕ and ψ can be expressed by
()
()

C. Solution of the Submerged Part of the Beam

We postulate the following solution of (1):
()
describing the lateral deflexion of the submerged beam
()
Substitution into (1) and taking into account (28) yield
()
The software Mathematica was used in order to obtain (32) solution of the above equation. Similarly, we can also find (33) solution of (2) describing the lateral deflexion of the beam in vacuum.

D. Frequency Equation

For nontrivial solution, the determinant of the matrices M must be equal to zero
This equation indicates a relationship between the kinematic fluid viscosity ν, fluid density ρ, angular frequency ω, and the elastic constants. For given material and geometric properties, (DM) constitutes an implicit transcendental function of n and ω. The roots ω may be computed for a fixed n.

E. Auxiliary Coefficients

The coefficients Υ, I1, I2, I3, and I4 in (38) are defined as follows:
()
where
()

F. The Elements of the M Matrix

The matrix M in (13) is defined as follows:
()
where
()
where
()

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.