Volume 2016, Issue 1 4504817

Research Article

Open Access

On Gravitational Entropy of de Sitter Universe

S. C. Ulhoa,

Corresponding Author

S. C. Ulhoa

[email protected]

orcid.org/0000-0001-9994-958X

Institute of Physics, University of Brasília, 70910-900 Brasília, DF, Brazil unb.br

Search for more papers by this author

E. P. Spaniol,

E. P. Spaniol

orcid.org/0000-0002-0619-9327

Institute of Physics, University of Brasília, 70910-900 Brasília, DF, Brazil unb.br

Department of Civil Engineering, FATECS, University Center of Brasília (UniCEUB), 70790-075 Brasília, DF, Brazil uniceub.br

University Center of the Federal District (UDF), Department of Civil Engineering, 70390-045 Brasília, DF, Brazil udf.edu.br

Search for more papers by this author

S. C. Ulhoa,

Corresponding Author

S. C. Ulhoa

[email protected]

orcid.org/0000-0001-9994-958X

Institute of Physics, University of Brasília, 70910-900 Brasília, DF, Brazil unb.br

Search for more papers by this author

E. P. Spaniol,

E. P. Spaniol

orcid.org/0000-0002-0619-9327

Institute of Physics, University of Brasília, 70910-900 Brasília, DF, Brazil unb.br

Department of Civil Engineering, FATECS, University Center of Brasília (UniCEUB), 70790-075 Brasília, DF, Brazil uniceub.br

University Center of the Federal District (UDF), Department of Civil Engineering, 70390-045 Brasília, DF, Brazil udf.edu.br

Search for more papers by this author

First published: 18 July 2016

https://doi.org/10.1155/2016/4504817

Citations: 4

Academic Editor: Sergei D. Odintsov

Share a link

Email
Wechat
Bluesky

Abstract

The paper deals with the calculation of the gravitational entropy in the context of teleparallel gravity for de Sitter space-time. In such a theory it is possible to define gravitational energy and pressure; thus we use those expressions to construct the gravitational entropy. We use the temperature as a function of the cosmological constant and write the first law of thermodynamics from which we obtain the entropy. In the limit Λ ≪ 1 we find that the entropy is proportional to volume, for a specific temperature’s choice; we find that ΔS ≥ 0 as well. We also identify a phase transition in de Sitter space-time by analyzing the specific heat.

1. Introduction

The idea of black hole thermodynamics started with the pioneering works of Bekenstein and Hawking [1, 2]. It was noted that the area of the event horizon behaves as an entropy. Together with such discovery it was also noted that it has a specific temperature. Thus it radiates and evaporates leading to a loss of the information inside the black hole, which apparently violates the second law of thermodynamics. It was the so-called information paradox [3]. Dolan has pointed out that such study was incomplete without the term pdV in the first law of thermodynamics [4]. However the concept of gravitational pressure is difficult to establish as the very idea of gravitational energy. The matter of the definition of gravitational energy has a long story and yet it is a very controversial theme. The main approaches in this subject are Komar integrals [5], ADM formalism [6], and quasi-local expressions [7, 8]. In opposition to general relativity, in teleparallel gravity those quantities can be well defined.

Teleparallel Equivalent to General Relativity (TEGR) is an alternative theory of gravitation constructed out in terms of the tetrad field on Weitzenböck geometry. It was first proposed by Einstein in an attempt to derive a unified field theory [9]. Later it was revived with a paper entitled “New General Relativity” [10]; since then a lot of improvement has been made in the understanding of gravitational energy and the role of torsion [11, 12]. In the context of TEGR it is possible to define an expression for gravitational energy which is invariant under coordinates transformation and dependent on the reference frame. Those features are present in the special theory of relativity and there is no physical reason to abandon such ideas once one has dealt with a gravitational theory. Using the field equations of TEGR, it is possible to define an expression for the gravitational pressure. Therefore a natural extension is to define an expression for the gravitational entropy. The advantage of this procedure is defining an entropy in terms of purely thermodynamical quantities such as energy and pressure. This will be our main goal in this paper, for de Sitter Universe. This Universe model is important because it describes an expanding empty space. Thus it is possible to shed light on the vacuum energy and cosmological inflationary models.

The paper is organized as follows. In Section 2, we present the main ideas of teleparallel gravity. From field equation we derive the total energy and pressure. In Section 3, we calculate such quantities for de Sitter Universe, and then we use the first law of thermodynamics to get the gravitational entropy. To achieve such aim, we have interpreted the temperature of the system as a function of the cosmological constant. Finally we present our concluding remarks in Section 4.

Notation. Space-time indices μ, ν, … and SO(3,1) indices a, b, … run from 0 to 3. Time and space indices are indicated according to μ = 0, i, a = (0), (i). The tetrad field is denoted by and the determinant of the tetrad field is represented by . In addition we adopt units where G = k_b = c = 1, unless otherwise stated.

2. Teleparallel Equivalent to General Relativity (TEGR)

Teleparallel gravity is a theory entirely equivalent to general relativity; however it is formulated in the framework of Weitzenböck geometry rather than in terms of Riemann geometry. Weitzenböck geometry is endowed with the Cartan connection [13], given by

, where

is the tetrad field; thus the torsion tensor can be calculated in terms of this field by

()

Such a geometry keeps a relation to a Riemannian manifold; for instance, we note the Cartan connection and Christoffel (

) symbols are related by a mathematical identity, which reads

()

where

()

is the contortion tensor. The tetrad field, which is the dynamical variable of the theory, is obtained from the metric tensor. Thus Weitzenböck geometry is less restrictive than Riemann geometry; for each metric tensor it is possible to construct an infinite number of tetrad fields. This apparent arbitrary behavior is amended once we recall the interpretation of the tetrad field. The component

is associated with the four-velocity of the observer; then for each reference frame there exists only one tetrad field. In fact we have to make use of the acceleration tensor to completely settle the state of an observer [14], since it could be in rotation as well as in translation.

If one tries to construct the curvature from the Cartan connection, he/she will find out that it vanishes identically. Hence the Weitzenböck geometry is described by a vanishing curvature and the presence of torsion. The Riemann geometry, as is well known, has vanishing torsion and a nonvanishing curvature tensor. Therefore making use of identity (2) to construct the scalar curvature, it leads to

()

where e is the determinant of the tetrad field,

, and R(e) is the scalar curvature constructed out in terms of such a field. It should be noted that the metric tensor alone does not establish a geometry. From the above identity, we see that it is possible to construct a tetrad field adapted to a specific reference frame which induces, for the same metric tensor, both a curvature in Riemannian manifold and torsion in a Weitzenböck geometry. By means of the very same above identity, it is possible to find the counterpart of Hilbert-Einstein Lagrangian density for teleparallel gravity; thus, up to a total divergence (which plays no role in the field equations), it reads

()

where k = 1/16π and

stands for the Lagrangian density for the matter fields. This Lagrangian density can be rewritten as

()

where

()

The field equations can be derived from Lagrangian (6) using a variational derivative with respect to e^aμ; they read

()

where

. The field equations may be rewritten as

()

where

and

()

In view of the antisymmetry property Σ^aμν = −Σ^aνμ, it follows that

()

Such equation leads to the following continuity equation:

()

Therefore we identify t^λμ as the gravitational energy-momentum tensor [15, 16].

Then, as usual, the total energy-momentum vector is defined by [17]

()

where V is a volume of the three-dimensional space. It is important to note that the above expression is invariant under coordinate transformations and it transforms like a 4-vector under Lorentz transformations. The energy-momentum flux is given by the time derivative of (13); thus by means of (12) we find

()

If we assume a vacuum solution, for example, a vanishing energy-momentum tensor of matter fields, then we have

()

which is the gravitational energy-momentum flux [18]. Using field equations (9), the total energy-momentum flux reads

()

Now let us restrict our attention to the spatial part of the energy-momentum flux, that is, the momentum flux; we have

()

where

()

we note that the momentum flux is precisely the force; hence, since dS_j is an element of area, we see that −ϕ^(i)j represents the pressure, along the (i) direction, over an element of area oriented along the j direction [16]. It should be noted that all definitions presented in this section follow exclusively from field equations (9).

We point out that general relativity and teleparallel gravity are equivalent only concerning dynamical features. This means that both theories will predict the same behavior of a test particle around a mass distribution. In other words both of them will agree in the classical experimental tests such as Mercury’s perihelion deviation and the bending of light. However predictions concerning the gravitational field features are strictly different, such as gravitational energy, momentum, and angular momentum. For instance, there is no analogous tensor in general relativity equivalent to the gravitational energy-momentum tensor in (10). The main reason for this is that some of the tensorial quantities in teleparallel gravity are analogous to connections in Riemannian geometry which gives rise to pseudo-tensors describing gravitational energy and momentum. Particularly there is no tensorial form, in Riemannian geometry, of T_aμν on Weitzenböck geometry. The problem of defining gravitational energy in general relativity is a long-standing one; as a consequence any thermodynamical attempt to define a gravitational entropy would be plagued by the same problems. On the other hand such a quantity is natural in teleparallel gravity; thus our approach has several advantages. In Table 1, we chart the features of general relativity and teleparallel gravity.

	General relativity	Teleparallel gravity
Field equations	G_μν = kT_μν	Equivalent
Gravitational energy-momentum tensor	Nonexistent	t^aμ
Gravitational energy	ADM/Komar expressions	Defined from t^aμ
Gravitational pressure	Nonexistent	Defined from t^aμ
Gravitational entropy	Proportional to the area	Defined from t^aμ

We stress out that the definition of entropy in general relativity is not of general validity since it demands the existence of matter as in the black hole context. It is possible to force both definitions to agree at some point by the choice of temperature; however it seems an arbitrary procedure.

3. The Gravitational Entropy for de Sitter Space-Time

The de Sitter space-time is defined by the following line element:

()

where

and Λ is the cosmological constant. Such a space-time works as a model of an expanding Universe; thus many inflationary models of the early Universe make use of this feature [19–21].

Let us choose the following tetrad field adapted to a stationary reference frame:

()

where A = (1 − r²/R²) ^1/2 and its determinant is e = r²sin⁡θ. It is worth recalling some ideas on how to choose the tetrad field. It is well known that for a given metric tensor there exist an infinity number of possible tetrads. On the other hand given a world line of an observer the tetrad field can be transported along such a curve; in particular the a = (0) component of the tetrad field remains tangent to the curve. Thus it is possible to associate such a component with the 4-velocity of the observer. Hence the tetrad field is adapted to a reference frame. Mashhoon generalized such a concept in [22, 23]; there the absolute derivative of the tetrad field is defined as

()

where

is the acceleration tensor. The component Φ_(0)(i) defines the tangential acceleration while Φ_(i)(j) establishes the rotational acceleration.

The nonvanishing components of the torsion tensor are

()

In order to calculate the gravitational energy and pressure we need the components Σ^μνλ; thus after some algebraic manipulation we find that the nonvanishing ones are

()

Hence, substituting the above components into (13) for a = (0), it is possible to find the total energy and it reads

()

where r₀ is the radius of a spherical 3-dimensional hypersurface of integration. In addition we have made the identification E ≡ P⁽⁰⁾. It should be noted that such expression already appeared in [24].

Similarly the radial pressure can be constructed from the components ϕ^(i)j which is given in terms of the components in (23). Thus after some simple calculations, we find

()

Then we construct a radial ϕ, which is denoted by ϕ^(r)1; by means of the relation

()

it yields

()

The radial pressure is given by

()

and therefore, we obtain

()

Once the energy and pressure are given, we can turn our attention to the entropy itself. It is a thermodynamical potential linked to the variation of energy and volume; that is,

()

where T is the temperature (considered constant a priori) and S is the entropy. The change in the volume is realized through the variation of r₀; thus p(r₀, θ, ϕ)d³x → p(r₀)dr₀, once we perform an integration over the θ and ϕ variables. The total energy also changes with the variation of r₀. In this system we have two parameters r₀ and the cosmological constant: the first one is linked to the volume while the second one has to play the role of a temperature. As a consequence we suppose the temperature could be given by an arbitrary function of the cosmological constant, T = f(Λ). Therefore the energy will vary with the change of the temperature. Then the first law of thermodynamics simply reads

()

then the gravitational entropy is given by

()

which yields

()

In Figure 1 we plotted the entropy as a function of r₀. We normalized the horizon radius, R = 1; thus the choice of temperature as dependent on the cosmological constant will not affect the entropy. We see a divergence when the space reaches the horizon volume which is an expected behavior.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Entropy versus r₀.

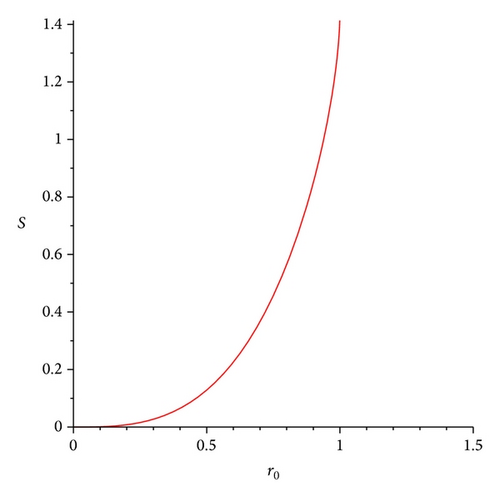
Next we will analyze how the entropy can depend on the horizon area and two remarkable choices for the temperature. The first one is the well-known temperature of de Sitter space-time, and the second one is based on an attempt to obtain a gravitational entropy independent of the temperature.

3.1. Entropy and Horizon Area

If one assumes the Hawking area dependence for the entropy then it is possible to analyze the consequences of this fact in the context of teleparallel gravity as performed in [25]; however in this subsection we are interested in obtaining such a dependence assuming the existence of a gravitational energy and pressure. We point out that, to obtain the entropy, one should consider it as a thermodynamical potential which depends on the energy and the volume; thus the temperature should be constant. For instance, if we intend to obtain the heat capacity then we should consider the energy as the potential; only then can the temperature change.

If we use (31) together with the expressions of energy and pressure, then it yields

()

Since dA = 8πr₀dr₀ we get

()

Hence in order to obtain dS = dA/4, where A is the horizon area, the algebraic equation

()

must be satisfied for r₀ = R which is not true. Therefore the entropy is not necessarily a quarter of the horizon area. On the other hand the entropy can be proportional only to the spatial area. This is achieved by finding a solution for the above equation. For instance, with the choice πTR = 1, we find r₀ = 0.47R.

In [26] an entropy is constructed for de Sitter space-time. We point out that the procedure adopted in such a reference is an attempt to identify the term pdV which seems to be missing in gravitational thermodynamics as discussed by Dolan [4]. In order to perform such an aim it is usual to assume the Hawking entropy and as a consequence obtain the other terms in the first law of thermodynamics. In this paper we follow the opposite path; we use the gravitational pressure defined in the framework of teleparallel gravity to find the entropy. In this sense it is mandatory to have a satisfactory definition of gravitational energy which can also be found in teleparallel gravity.

Thus in our opinion the Hawking entropy is a nonthermodynamical expression, since it is defined in a context where some trouble to define gravitational energy and pressure is observed. Clearly the dependency of the entropy on the horizon area is an important theoretical insight in this problem. In fact it has been used to propose an analog of Higgs mechanism in cosmology [27], where the de Sitter space plays an important role. In [28] the authors deal with a statistic mechanics approach of de Sitter entropy which is proportional to horizon area. In such cases the problem of composing the full thermodynamical picture with energy, pressure, and entropy is a serious obstacle. Hence, once there is no experimental evidence to support the Hawking expression, our expression should be considered as a candidate to represent the gravitational entropy.

3.2. de Sitter Temperature

In this subsection we will use the temperature of de Sitter space-time which is defined as

[29, 30]. If we analyze the gravitational entropy in the regime where Λ ≪ 1, then we will have

()

where V is the 3D volume.

Now let us allow the temperature Λ to change. With such a procedure we are interested in the specific heat at constant volume C_V. Thus

()

where keeping a constant volume means having a constant r₀, since

. Therefore we have

()

this quantity gives the information on how the gravitational energy changes on the variation of the cosmological constant. It should be noted that specific heat goes to zero when the temperature vanishes. At this point we can see a discontinuity in the specific heat which, by the way, establishes a phase transition of the first order between thermodynamical states defined by E, S, p, and T, as is well known. Thus the critical temperature is given by

()

Thus we see that the older the Universe is the easier it is to expect a phase transition since the critical temperature will be smaller with the Universe’s expansion.

3.3. Temperature as the Cosmological Constant

In this subsection we will take the cosmological constant as the temperature, T = αΛ, where α is a dimensional constant. Thus we use this in expression (33) and, in the limit Λ ≪ 1, it yields

()

which is proportional to the volume rather than the area as obtained in [2] in the context of black holes. It should be noted that, in this limit, ΔS ≥ 0, since de Sitter Universe is in expansion. We see that such a choice, at a proper limit, leads to an entropy independent of the temperature. Hereafter we will make α = 1.

The specific heat at constant volume C_V, using this temperature, is given by

()

it should be noted that C_V → V/8π when T → 0. In this context the critical temperature is given by

()

thus a phase transition during inflation era could have happened since the space-time experimented such a great expansion then. In this sense a rapid expansion could be driving a phase transition in the primordial Universe.

4. Conclusion

In this paper we have obtained the gravitational entropy for de Sitter space-time in the framework of teleparallel gravity. Such a result was obtained by purely thermodynamical quantities; that is, using concepts such as energy and pressure that can be defined in TEGR, we have derived an expression for the entropy. To obtain this we have used the first law of thermodynamics in which the temperature is a function of the cosmological constant. We have assumed that because we have only two parameters in this system, the radius of the hypersurface of integration, r₀, which dictates how the volume varies, and the cosmological constant, Λ. We investigated the entropy in the limit Λ ≪ 1 for two definitions of temperature: the first one was the well-known de Sitter temperature and the second one was the very cosmological constant. We have obtained that the entropy is proportional solely to the 3D volume, with this last temperature’s choice, yet the entropy always increases in this case; for example, ΔS ≥ 0. Then we have relaxed the condition T = Λ = const. to obtain the specific heat at constant volume for each case. If we have chosen the temperature as constant then, in the limit Λ ≪ 1, it would be impossible to establish a specific heat. We have found that the specific heat goes to zero in the limit T → 0 in the first case and that it goes to a constant, proportional to the 3D volume, in the second case, in the same limit. By the analysis of the specific heat we conclude that the de Sitter Universe performed a phase transition at some point of its evolution. The entropy also diverges with a critical temperature which corroborates such an idea of phase transition. We note that in both cases the critical temperatures lead to the same critical cosmological constant which is . We also showed that the entropy, defined in teleparallel gravity, is not necessarily equal to the area of the event horizon. It is not the case of Hawking expression which is constructed out in the context of general relativity where one cannot deal with meaningful expressions of gravitational energy and pressure. The choice to calculate the entropy of a de Sitter space-time was guided by two reasons. The first one is that the most accepted expression of entropy is based on nonthermodynamical approach in which the physical meaning relies on matter fields. Thus analyzing an expanding empty space we could shed light on the very nature of gravitational field. The second reason is that it is believed that any quantum gravity theory should break the Lorentz invariance [31]. We speculate that in constructing an effective theory of gravitation, in order to quantize it, the torsion tensor will self-interact with the geometry of space-time which could be interpreted as a mean field representing the spin of the matter distribution.

Competing Interests

The authors declare that they have no competing interests.

References

1 Bekenstein J. D., Black holes and entropy, Physical Review. D. (1973) 7, 2333–2346, https://doi.org/10.1103/physrevd.7.2333, MR0366343, 2-s2.0-33750485765.
10.1103/PhysRevD.7.2333
Web of Science® Google Scholar
2 Hawking S. W., Black holes and thermodynamics, Physical Review D. (1976) 13, no. 2, 191–197, https://doi.org/10.1103/PhysRevD.13.191.
10.1103/PhysRevD.13.191
Web of Science® Google Scholar
3 Hawking S. W., Information loss in black holes, Physical Review D. (2005) 72, no. 8, 4, 084013, https://doi.org/10.1103/physrevd.72.084013, MR2184305.
10.1103/PhysRevD.72.084013
CAS Web of Science® Google Scholar
4 Dolan B. P., Pressure and volume in the first law of black hole thermodynamics, Classical and Quantum Gravity. (2011) 28, no. 23, 13, 235017, https://doi.org/10.1088/0264-9381/28/23/235017, MR2865360, 2-s2.0-81255179991.
10.1088/0264-9381/28/23/235017
Web of Science® Google Scholar
5 Komar A., Covariant conservation laws in general relativity, Physical Review Letters. (1959) 113, 934–936, MR0102403.
Google Scholar
6 Arnowitt R., Deser S., and Misner C., L. Witten, The dynamics of general relativity, Gravitation: An Introduction to Current Research, 1962, John Wiley & Sons, New York, NY, USA, 227–265.
Google Scholar
7 Brown J. D. and York J. W., Quasilocal energy and conserved charges derived from the gravitational action, Physical Review D. (1993) 47, no. 4, 1407–1419, https://doi.org/10.1103/physrevd.47.1407.
10.1103/PhysRevD.47.1407
CAS PubMed Web of Science® Google Scholar
8 Szabados L. B., Quasi-local energy-momentum and angular momentum in GR: a review article, Living Reviews in Relativity. (2004) 7, article 4, https://doi.org/10.12942/lrr-2004-4, 2-s2.0-3042826354.
10.12942/lrr-2004-4
Google Scholar
9 Einstein A., Auf die Riemann-Metrik und den Fern-Parallelismus gegründete einheitliche Feldtheorie, Mathematische Annalen. (1930) 102, no. 1, 685–697, https://doi.org/10.1007/bf01782370.
10.1007/BF01782370
Google Scholar
10 Hayashi K. and Shirafuji T., New general relativity, Physical Review D. (1979) 19, no. 12, 3524–3553, https://doi.org/10.1103/physrevd.19.3524, MR538567, 2-s2.0-0001117240.
10.1103/PhysRevD.19.3524
Web of Science® Google Scholar
11 Hehl F. W., P. G. Bergmann and V. de Sabbata, Four lectures on poincaré gauge field theory, Proceedings of the 6th School of Cosmology and Gravitation on Spin, Torsion, Rotation and Supergravity, May 1979, Erice, Italy, (Plenum Press, 1980).
Google Scholar
12 Hehl F. W., Lemke J., and Mielke E. W., J. Debrus and A. C. Hirshfeld, Two lectures on fermions and gravity, Geometry and Theoretical Physics, 1991, Springer, Berlin, Germany.
10.1007/978-3-642-76353-3_3
Google Scholar
13 Cartan E., P. G. Bergmann and V. de Sabbata, On a generalization of the notion of Riemann curvature and spaces with torsion, Cosmology and Gravitation: Spin, Torsion, Rotation, and Supergravity, 1980, 58, Plenum, 489–491, NATO ASIB Proc. 58, MR702709.
Google Scholar
14 Maluf J. W., Faria F. F., and Ulhoa S. C., On reference frames in spacetime and gravitational energy in freely falling frames, Classical and Quantum Gravity. (2007) 24, no. 10, 2743–2753, https://doi.org/10.1088/0264-9381/24/10/017, MR2319444.
10.1088/0264-9381/24/10/017
Web of Science® Google Scholar
15 de Andrade V. C., Guillen L. C. t., and Pereira J. G., Gravitational energy-momentum density in teleparallel gravity, Physical Review Letters. (2000) 84, no. 20, 4533–4536, https://doi.org/10.1103/physrevlett.84.4533, MR1757381.
10.1103/PhysRevLett.84.4533
CAS PubMed Web of Science® Google Scholar
16 Maluf J. W., The gravitational energy-momentum tensor and the gravitational pressure, Annalen der Physik. (2005) 14, no. 11-12, 723–732, https://doi.org/10.1002/andp.200510161.
10.1002/andp.200551711-1203
Web of Science® Google Scholar
17 Maluf J. W., da Rocha-Neto J. F., Toribio T., and Castello-Branco K. H., Energy and angular momentum of the gravitational field in the teleparallel geometry, Physical Review D. (2002) 65, no. 12, 12, 124001, https://doi.org/10.1103/physrevd.65.124001, MR1926186.
10.1103/PhysRevD.65.124001
CAS Web of Science® Google Scholar
18 Maluf J. W. and Faria F. F., On gravitational radiation and the energy flux of matter, Annalen der Physik. (2004) 13, no. 10, 604–616, https://doi.org/10.1002/andp.200410097, MR2092845.
10.1002/andp.20045161005
Google Scholar
19 Nakao K.-I., Nambu Y., and Sasaki M., Stochastic dynamics of new inflation, Progress of Theoretical Physics. (1988) 80, no. 6, 1041–1068, https://doi.org/10.1143/ptp.80.1041.
10.1143/PTP.80.1041
Google Scholar
20 Seery D., A parton picture of de Sitter space during slow-roll inflation, Journal of Cosmology and Astroparticle Physics. (2009) 2009, no. 5, article 021, https://doi.org/10.1088/1475-7516/2009/05/021.
10.1088/1475-7516/2009/05/021
Google Scholar
21 Lasenby A. and Doran C., Closed universes, de Sitter space, and inflation, Physical Review D. (2005) 71, no. 6, 063502, https://doi.org/10.1103/physrevd.71.063502, MR2138825.
10.1103/PhysRevD.71.063502
CAS Web of Science® Google Scholar
22 Mashhoon B. and Muench U., Length measurement in accelerated systems, Annalen der Physik. (2002) 11, no. 7, 532–547, https://doi.org/10.1002/1521-3889(200208)11:7<532::AID-ANDP532>3.0.CO;2-3, 2-s2.0-0036377458.
10.1002/andp.20025140706
Web of Science® Google Scholar
23 Mashhoon B., Vacuum electrodynamics of accelerated systems: nonlocal Maxwell′s equations, Annalen der Physik. (2003) 12, no. 10, 586–598, https://doi.org/10.1002/andp.200310028, MR2016922.
10.1002/andp.20035151002
Web of Science® Google Scholar
24 Ulhoa S. C., da Rocha Neto J. F., and Maluf J. W., The gravitational energy problem for cosmological models in teleparallel gravity, International Journal of Modern Physics. D. Gravitation, Astrophysics, Cosmology. (2010) 19, no. 12, 1925–1935, https://doi.org/10.1142/S021827181001813X, MR2727491, ZBL1204.83077.
10.1142/S021827181001813X
Google Scholar
25 Maluf J. W., Ulhoa S. C., and da Rocha-Neto J. F., Gravitational pressure on event horizons and thermodynamics in the teleparallel framework, Physical Review D. (2012) 85, no. 4, 044050, https://doi.org/10.1103/physrevd.85.044050.
10.1103/PhysRevD.85.044050
CAS Web of Science® Google Scholar
26 Padmanabhan T., Classical and quantum thermodynamics of horizons in spherically symmetric spacetimes, Classical and Quantum Gravity. (2002) 19, no. 21, 5387–5408, https://doi.org/10.1088/0264-9381/19/21/306, MR1939923.
10.1088/0264-9381/19/21/306
Web of Science® Google Scholar
27 Jazayeri S., Mukohyama S., Saitou R., and Watanabe Y., Ghost inflation and de Sitter entropy, https://arxiv.org/abs/1602.06511.
Google Scholar
28 Nozari K., Gorji M. A., Hosseinzadeh V., and Vakili B., Natural cutoffs via compact symplectic manifolds, Classical and Quantum Gravity. (2016) 33, no. 2, 21, 025009, https://doi.org/10.1088/0264-9381/33/2/025009, MR3461565.
10.1088/0264-9381/33/2/025009
Web of Science® Google Scholar
29 Deser S. and Levin O., Accelerated detectors and temperature in (anti-) de Sitter spaces, Classical and Quantum Gravity. (1997) 14, no. 9, L163–L168, https://doi.org/10.1088/0264-9381/14/9/003, MR1477799, ZBL0884.53059.
10.1088/0264-9381/14/9/003
Google Scholar
30 Figari R., Hoegh-Krohn R., and Nappi C. R., Interacting relativistic boson fields in the de Sitter universe with two space-time dimensions, Communications in Mathematical Physics. (1975) 44, no. 3, 265–278, https://doi.org/10.1007/BF01609830, MR0384010, 2-s2.0-33744730390.
10.1007/BF01609830
Web of Science® Google Scholar
31 Buchbinder I., Odintsov S., and Shapiro L., Effective Action in Quantum Gravity, 1992, Taylor & Francis.
Google Scholar

Citing Literature

All articles

On Gravitational Entropy of de Sitter Universe

Abstract

1. Introduction

2. Teleparallel Equivalent to General Relativity (TEGR)

3. The Gravitational Entropy for de Sitter Space-Time

3.1. Entropy and Horizon Area

3.2. de Sitter Temperature

3.3. Temperature as the Cosmological Constant

4. Conclusion

Competing Interests

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

On Gravitational Entropy of de Sitter Universe

Abstract

1. Introduction

2. Teleparallel Equivalent to General Relativity (TEGR)

3. The Gravitational Entropy for de Sitter Space-Time

3.1. Entropy and Horizon Area

3.2. de Sitter Temperature

3.3. Temperature as the Cosmological Constant

4. Conclusion

Competing Interests

References

Citing Literature

Figures

References

Related

Information