We formulated and analysed a mathematical model to explore the cointeraction between malaria and schistosomiasis. Qualitative and comprehensive mathematical techniques have been applied to analyse the model. The local stability of the disease-free and endemic equilibrium was analysed, respectively. However, the main theorem shows that if , then the disease-free equilibrium is locally asymptotically stable and the phase will vanish out of the host and if , a unique endemic equilibrium is also locally asymptotically stable and the disease persists at the endemic steady state. The impact of schistosomiasis and its treatment on malaria dynamics is also investigated. Numerical simulations using a set of reasonable parameter values show that the two epidemics coexist whenever their reproduction numbers exceed unity. Further, results of the full malaria-schistosomiasis model also suggest that an increase in the number of individuals infected with schistosomiasis in the presence of treatment results in a decrease in malaria cases. Sensitivity analysis was further carried out to investigate the influence of the model parameters on the transmission and spread of malaria-schistosomiasis coinfection. Numerical simulations were carried out to confirm our theoretical findings.

1. Introduction

Malaria is highly endemic in various parts of sub-Saharan Africa in which 85% of global malaria cases and 90% of malaria deaths occur [1]. Schistosoma mansoni (the causative agent of intestinal schistosomiasis) is also prevalent in many sub-Saharan African countries [2, 3], accounting for approximately one-third of the total cases of schistosomiasis in the region [4]. The disease is a major contributor to disease burden globally and affects low income countries with climates suitable for transmission seriously. It is a life-threatening disease caused by parasites that are transmitted to people by the bites of infected mosquitoes [4, 5]. The bites by mosquitoes have resulted in the death of a child from malaria every 30 secs according to the report by the World Health Organization (WHO) fact sheet (2009) [4, 5]. Plasmodium falciparum and Plasmodium vivax are the two common species and Plasmodium falciparum is the most deadly. Plasmodium falciparum malaria remains a major cause of mortality and morbidity in the tropics and subtropics areas of the globe [4, 6]. According to the 2009 world report, half of the world’s population is at risk of malaria, with an estimated 247 million cases that led to about 863,000 death in 2008 mostly among African children, a slight drop from 2006 statistics with the estimation that over 2000 young are lost every day across the globe [4]. This population made malaria the dominant parasitic disease of the tropics and one of the top three killer communicable diseases [4, 5, 7]. Malaria makes development to be very slow in several ways; it affects fertility, population growth, savings and investments, and worker productivity and causes absenteeism and premature mortality [4, 5, 7]. Malaria also affects fetal development during early stage of pregnancy in women due to loss of immunity. However, malaria is preventable and curable when treatment and prevention measures are sought early [4, 5, 7].

The disease, schistosomiasis, also known as bilharziasis or snail fever, is a parasitic disease that was first named bilharzia [8, 9] and it is prevalent in several regions of the developing world, predominantly Africa, South America, and Asia, with about 650 million people living in the endemic areas [10]. It is known that estimated 207 million people are infected, where 85 percent lives in underdeveloped areas of Africa [11], resulting in about 15,000 deaths annually presently [2]. Children below the age of 14 are the major victims of schistosomiasis infection in many parts of the world [10]. The basis of illness in victims is the eggs laid by the parasitic flat worms, that is, blood flukes of the genus Schistosoma [8]. The species of the water-borne flatworm or blood flukes known as schistosomes is the main type that initiates the human schistosomiasis, but Schistosoma mansoni, Schistosoma japonicum, and Schistosoma haematobium are the three major species that are found everywhere [8]. The urinary tract and kidneys as well as the reproductive systems are affected by the Schistosoma haematobium, and they are intense in Africa and the Middle East [8]. The most widely spread species is the Schistosoma mansoni while Schistosoma japonicum is chiefly found in Asia and these two cause chronic hepatic and intestinal fibrosis [8, 10]. When skin comes in contact with contaminated freshwater in which certain types of snails that carry the parasite are living then the infection can be established [8]. Whenever infected people urinate or defecate in the water, freshwater becomes contaminated by Schistosoma eggs [8]. The eggs hatch, and the parasites infect, mature, and reproduce inside the snails when the appropriate species of snails exist in the water [12]. The parasite eventually leaves the snail and go into the water where it can persist for about 48 hours [8, 12]. Schistosoma parasites, when wading, swimming, bathing, or washing, can enter the skin of anyone who comes in contact with contaminated freshwater [8, 12]. The parasites migrate through host tissue and develop into adult worms inside the blood vessels of the body for over numerous weeks [8, 12]. The worms mate and females produce eggs after maturity [8, 12]. Several of these eggs eventually travel to the bladder or intestine and are finally passed into the urine or stool [8, 12]. The schistosomiasis symptoms are caused by the body’s reaction to the eggs but not by the worms themselves [12, 13]. Eggs shed by the adult worms that do not pass out of the body can become lodged in the intestine or bladder, causing inflammation or scarring [12, 13]. Repeatedly infected children can acquire anemia, malnutrition, and learning difficulties [12, 13]. The parasite can as well damage the liver, intestine, spleen, lungs, and bladder even several years after infection [12, 13]. It is known at present that both malaria and intestinal schistosomiasis contribute to common epidemiological distributions and are currently posing a great task to public health and socioeconomic development throughout the tropical region [14]. The interactive pathology between malaria and S. mansoni has received increased investigation in the recent time, as a result of their coendemicities [1, 11, 15, 16]. It has been discovered that considerable S. mansoni infections are linked with a major increase in the incidence of malaria among school-age children [11]. In individuals infected with S. mansoni the technique responsible for the magnification of malaria is not yet fully understood [1, 9]. Thus, it is observed that the interface between the two diseases is perhaps set in motion by contradicting effects; the parasites possess the immunological cytokines; that is, the balance between Th1 and Th2 type immune responses which reduces immunological control of malaria may be altered by S. mansoni, while other methods are probable [1, 15, 17–19].

It is our view that this study represents the very first modeling work that presents a mathematical analysis of the qualitative dynamics of malaria-schistosomiasis coinfection. There are few studies done on the malaria-schistosomiasis coinfection model so far. In [20], a coepidemic model of malaria and S. mansoni transmission dynamics is established, where the model reports major epidemiological coupling between the two diseases in terms of aggravated malaria incidence among individuals with S. mansoni extreme egg output. Their model was factored for S. mansoni extreme-risk endemic areas, applying epidemiological and clinical data of the relationship between S. mansoni and malaria among children in sub-Saharan Africa. They also assessed the potential influence of the S. mansoni malaria interface and mass treatment of schistosomiasis on malaria prevalence in coendemic areas.

In this paper, we develop a mathematical model of the interplay between malaria and S. mansoni in which we have modeled the malaria transmission and the S. mansoni together as coendemic deterministic model. Our aim here is to study and analyse a mathematical model of malaria-schistosomiasis transmission model. Additionally, there are some important differences between the model in [16] and the one in this paper. This paper is organized as follows: we present a malaria-schistosomiasis coinfection transmission model formulation in Section 2, where the general mathematical framework, notations, and model equations were analysed with the basic properties of the models and their analysis. In Section 3, we present the existence of steady state solution. In Section 4, the basic reproduction number and stability were derived and carried out. Sensitivity analysis of the model was performed to determine the most important parameters that influence R₀ in Section 5. In Section 6, we show our numerical simulation results while, in Section 7, we discussed our conclusions and recommendations.

2. Model Formulation

In this model, we denote the total human population by N_h and subdivide it into the following subclasses of individuals who are susceptible (S_H), individuals with malaria symptoms only (i.e., who are already infected and infective with malaria parasite) (I_m), individuals infected with schistosomiasis only (I_hs), individuals infected with both malaria and schistosomiasis (V_ms), individuals who recovered from malaria only (R_m), individuals who recovered from schistosomiasis only (R_hs), and individuals who recovered from both malaria and schistosomiasis such that N_h = S_H + I_m + I_hs + V_ms + R_m + R_hs + R_ms. The total snail population is denoted by N_s, which comprises susceptible snails (S_s) and infected as well as infectious snails (I_s). That is, N_s = S_s + I_s. The total mosquito population is denoted by N_v, which comprises susceptible mosquitoes (S_v) and infected as well as infectious mosquitoes (I_v). That is, N_v = S_v + I_v.

The population of susceptible humans is generated through birth (at a constant per capita rate b_H), by the loss of immunity to the malaria disease only (at a constant per capita rate γ), loss of immunity to the schistosomiasis disease only at a rate k, and loss of immunity to malaria and schistosomiasis disease at a rate φ. It is reduced by natural death (at a rate d_H) and through the rate of acquiring malaria through contact with infectious mosquitoes (at a rate β₁ϵ_hσ), where β₁ is the transmission probability per bite, ϵ_h is the per capita biting rate of mosquitoes, and σ is the contact rate of mosquito per human per unit time. It is also reduced by rate of acquiring schistosomiasis through contact with infected snails (at a rate β₂). Hence, the rate of change of population of susceptible humans is given by

()

The rate of change of the population of individuals with malaria only is increased by the rate of acquiring malaria through contact with infectious mosquitoes (at a rate β₁ϵ_hσ) and by the rate of acquiring schistosomiasis through contact with infectious snail (at a rate β₂) It is also reduced by human spontaneous recovery (at a rate ω). It is also reduced by the disease induced death rate (at per capita rate θ) and by the natural death rate (at per capita rate d_H). Hence it is given by

()

The rate of change of the population of individuals infected with schistosomiasis only is increased by the rate of acquiring schistosomiasis through contact with infectious snail (at a rate β₂) and decreased by infected mosquitoes (at a rate β₁ϵ_hσ) and by human spontaneous recovery from schistosomiasis only (at a rate q_H). It is also reduced by the disease induced death rate (at per capita rate ρ_H) and by the natural death rate (at per capita rate d_H). Hence it is given by

()

The rate of change of the population of individuals infected with schistosomiasis and malaria is increased by the rate of acquiring malaria by infected mosquitoes (at a rate β₁ϵ_hσ) and schistosomiasis through contact with infectious snails (at a rate β₂) and reduced by human spontaneous recovery from schistosomiasis only (at a rate α). It is also reduced by the malaria disease induced death rate (at per capita rate m) and schistosomiasis induced death rate (at per capita rate r) and by the natural death rate (at per capita rate d_H). Hence it is given by

()

The individuals who recovered from malaria only is generated following a human spontaneous recovery (at a rate ω) and by the dually infected individuals who recovered from malaria only at a rate (ϕ(1 − α)) decreased by loss of immunity (at a rate γ) and by natural death (at a rate d_H). Then

()

The individuals who recovered from schistosomiasis only are generated following a human spontaneous recovery (at a rate q_H) and by the dually infected individuals who recovered from schistosomiasis only at a rate ((1 − ϕ)(1 − α)) decreased by loss of immunity (at a rate γ) and by natural death (at a rate d_H). Then

()

The individuals who recovered from malaria and schistosomiasis are generated following a human spontaneous recovery (at a rate α) decreased by loss of immunity (at a rate φ) and by natural death (at a rate d_H). Then

()

Susceptible snail population is generated by the birth of snails (at a per capita rate of b_s). It is reduced by rate of acquiring schistosomiasis through contacts with infected humans at a rate β₃, where η₁ is a modification parameter. It is also reduced by natural death (at a rate d_s). Thus,

()

The population of infected snail is increased by rate of acquiring schistosomiasis through contacts with infected humans at a rate β₃ and decreased by the natural death rate (at a rate d_s), where η₁ is a modification parameter. Hence, it is given by

()

Susceptible mosquito population is generated by the birth of mosquitoes (at a per capita rate of b_v). It is reduced by rate of acquiring malaria through contacts with infected humans at a rate β₄ϵ_vσ, where β₄ is probability for a vector (mosquito) to get infected by an infectious human, where η₂ is a modification parameter. It is also reduced by natural death (at a rate d_v). Thus,

()

The population of infected mosquito is increased by rate of acquiring malaria through contacts with infected humans at a rate β₂ϵ_vσ and decreased by the natural death rate (at a rate d_v), where η₂ is a modification parameter. Hence, it is given by

()

2.1. The Full Schistosomiasis-Malaria Coinfection Model

Bringing the above formulation and assumptions together leads to the following set of ordinary differential equations which may be a new malaria-schistosomiasis coinfection model:

()

subject to the initial conditions S_H(0) = S_H,0, I_m(0) = I_m,0, I_hs(0) = I_hs,0, V_ms(0) = V_ms,0, R_m(0) = R_m,0, R_hs(0) = R_hs,0, R_ms(0) = R_ms,0, S_s(0) = S_s,0, I_s(0) = I_s,0, S_v(0) = S_v,0, and I_v(0) = I_v,0.

We describe the associated model variables and parameters in the following list and Table 1.

Table 1. Table showing numerical values of sensitivity Indices.

Parameter	Parameter values	Sensitivity to
θ	0.05	−0.00000000000186
β₁	0.8333	+1.0
β₂	0.406	+1.0
β₃	0.004	+1.0
β₄	0.09	+0.99
b_v	1000	+0.74
d_H	0.00004	−2.0
ϵ_v	0.2	+1.0
σ	0.502	+2.0
ϵ_h	0.2	+1.0
q_H	0.56	−0.99
ρ_S	0.0004012	−0.876
ρ_H	0.0039	−0.0069
d_v	0.1429	−0.23
b_s	200	+1.0
b_H	100	+2.0
d_s	0.0000569	−0.11
ω	0.05	−0.91

Variables in the Model

S_H: susceptible human
I_m: human infected with malaria only
I_hs: human infected with schistosomiasis only
V_ms: human infected with malaria and schistosomiasis only
R_m: human recovered from malaria only
R_hs: human recovered from schistosomiasis only
R_ms: human recovered from malaria and schistosomiasis only
S_s: susceptible snail
I_s: infected snail
S_v: susceptible mosquito
I_v: infected mosquito

2.2. Qualitative Analysis of the Full Schistosomiasis-Malaria Coinfection Model

The schistosomiasis-malaria coinfection model (12) will be analysed in a biologically feasible region for both humans, snail, and mosquito populations. Hence, for it to be epidemiologically well posed, it is necessary to show that all its state variables are nonnegative for all time t > 0.

2.3. Positivity of the Solution

Theorem 1. If the initial value for S_H ≥ 0, I_m ≥ 0, I_hs ≥ 0, V_ms ≥ 0, R_m ≥ 0, R_hs ≥ 0, R_ms ≥ 0, S_s ≥ 0, I_s ≥ 0, S_v ≥ 0, and I_v ≥ 0 then the solutions (S_H(t), I_m(t), I_hs(t), R_hs(t), V_ms(t), R_m(t), R_hs(t), R_ms(t), S_s(t), I_s(t), S_v(t), I_v(t)) of the schistosomiasis only model (16) are nonnegative for all t > 0.

Proof. We let Γ = sup⁡ {t > 0 : S_H(t) > 0, I_m(t) > 0, I_hs(t) > 0, V_ms(t) > 0, R_m(t) > 0, R_hs(t) > 0, R_ms(t) > 0, S_s(t) > 0, I_s(t) > 0, S_v(t) > 0, I_v(t) > 0}.

Since the variables S_H(0) > 0, I_m(0) > 0, I_hs(0) > 0, V_ms(0) > 0, R_m(0) > 0, R_hs(0) > 0, R_ms(0) > 0, S_s(0) > 0, I_s(0) > 0, S_v(0) > 0, and I_v(0) > 0 then, Γ > 0. If Γ < ∞, then S_H, I_m, I_hs, V_ms, R_m, R_hs, R_ms, S_s, I_s, S_v, I_v are equal to zero at Γ. It follows from the first equation of the system (12) that

()

Therefore,

()

Hence

()

Also

()

Now,

()

And then

()

Now,

()

Furthermore,

()

Now,

()

Also

()

Therefore

()

Hence

()

so that

()

Also,

()

Therefore

()

Hence

()

so that

()

Also,

()

Then,

()

Hence

()

so that

()

Also,

()

Therefore,

()

Then, we have

()

Similarly,

()

Therefore,

()

so that

()

for all t > 0.

Also,

()

Therefore,

()

Then, we have

()

Similarly,

()

Therefore,

()

so that

()

for all t > 0.

2.4. Boundedness of the Solution

Theorem 2. All solutions (S_H(t), I_m(t), I_hs(t), V_ms(t), R_m(t), R_hs(t), R_ms(t), S_s(t), I_s(t), S_v(t), I_v(t)) of the malaria-schistosomiasis coinfection model (12) are bounded. Therefore, from (12) if

()

then N_s = S_s + I_s, N_v = S_v + I_v, and N_h = S_H + I_m + I_hs + V_ms + R_hs + R_m + R_hs + R_ms.

Proof. For the proof of boundedness, we note that 0 < I_m(t) ≤ N_h(t), 0 < I_hs(t) ≤ N_h(t), 0 < V_ms(t) ≤ N_h(t), 0 < I_s(t) ≤ N_s(t), and 0 < I_v(t) ≤ N_v(t). We add the first eight equations and the last two equations of the malaria-schistosomiasis coinfection model (12) and yield

()

All solutions of model (12) are bounded. The feasible region for the human population is given by Γ_h = {S_H, I_m, I_hs, V_ms, R_hs, R_m, R_hs, R_ms∣S_H + I_m + I_hs + V_ms + R_hs + R_m + R_hs + R_ms ≤ b_H/d_H, 0 ≤ S_H ≤ S_H(t) ≤ b_H/d_H, I_hs ≥ 0, R_hs ≥ 0}. And the feasible region for the snail population is given by

()

And the feasible region for the mosquito population is given by

()

Therefore,

()

Hence,

()

2.5. Invariant Region

Here, we analysed the malaria-schistosomiasis only model (12) in a biologically feasible region. Hence the system of (12) is split into three parts, namely. We have the human population (N_h: with N_h = S_H + I_m + I_hs + V_ms + R_hs + R_m + R_hs + R_ms), the snail (vector) population (N_s: with N_s = S_s + I_s), and the mosquito (vector) population (N_v: with N_v = S_v + I_v). Let us consider the feasible region as

()

with

()

We take the following steps to reaffirm the positive invariance of Γ (i.e., solution in Γ remains in Γ for all t > 0). The rate of change of humans, snails, and mosquitoes population is given in (12) and it follows that

()

By the standard comparison theorem we obtain

()

In particular, N_h(t) ≤ b_H/d_H if N_h(0) ≤ b_H/d_H, N_s(t) ≤ b_s/d_s if N_s(0) ≤ b_s/d_s, and N_v(t) ≤ b_v/d_v if N_v(0) ≤ b_v/d_v. Therefore, the region Γ is positively invariant. Hence, it is enough to consider the dynamics of the flow generated by (12) in Γ. Thus, the model can be considered to be epidemiologically and mathematically well posed in this region. Therefore every solution of the malaria-schistosomiasis coinfection model (12) with initial data (conditions) in Γ remains in Γ. The summary of this result is given below.

Theorem 3. The region is positively invariant for the malaria-schistosomiasis coinfection model (12) with nonnegative initial conditions in .

3. Existence of Steady States Solution

We analysed the model equation (12) in this section qualitatively to investigate the condition of existence of equilibrium points. We would like to know what will eventually happen to the disease in the long run. The question that will arise is (i) will the disease (malaria-schistosomiasis disease) die out? Or (ii) will it be established in the population and become endemic? In order to answer these questions we have to investigate the long-term behaviour of the solutions. This behaviour depends largely on the equilibrium points, that is, time-independent solutions of the system. Since these solutions do not depend on time, we set

()

Therefore, we have the equilibrium solution

()

This equilibrium exists for all values of the parameters. Since I_hs = R_hs = I_s = 0 it implies that the disease will disappear from the population. Thus, this equilibrium is referred to as the disease-free equilibrium (DFE).

3.1. Existence of Disease-Free Equilibrium Point (DFE)

We analysed the system qualitatively by studying the system of equation in closed set

()

A qualitative study of the system exists in two forms, namely,

(i)
the disease-free (dies out),
(ii)
endemic.

When the malaria-schistosomiasis disease dies out naturally, the solution asymptotically tends to a disease-free equilibrium D_MS of the form D_MS = (S_H = b_H/d_H, I_m = 0, I_hs = 0, V_ms = 0, R_hs = 0, R_m = 0, R_hs = 0, R_ms = 0, S_s = b_s/d_s, I_s = 0, S_v = b_v/d_v, I_v = 0). Hence, the threshold that determines the stability of this equilibrium is the reproduction number (which is the average number of secondary infections caused by a single infectious individual during their entire infectious lifetime).

4. The Basic Reproduction Number

Whenever , each individual releases on average less than one infected individual and therefore the disease (malaria-schistosomiasis only) dies out. Whenever , each individual release more than one new infected individual and therefore the disease is able to invade the susceptible population. This allows us to determine the effectiveness of control measures. Epidemiologically, the reproductive number tells us how many secondary cases will one infected individual or vector produce in an entirely susceptible population of hosts and vectors, in other words, to determine the number of infected people that are generated by the introduction of a single infected person into a susceptible population. We need the computation of the basic reproduction number to assess the stability of the disease-free equilibrium (DFE) and the endemic equilibrium point (EEP). The basic reproduction number for particular infections is dependent on the biological characteristics of the disease and on the behavioural pattern of the population. When there is a high transmission of the disease per unit time and durations of the infectious period, the basic reproduction number increases.

Proposition 4. The value of the basic reproduction number is .

Proof. The argument uses the approach of the next generation matrix (see [21]). Suppose

()

which results into

()

where F is the rate of appearance of new infections in one compartment and V is the transfer of individuals and mosquitoes into one compartment which is a Jacobian matrix evaluated at D_0s and the Jacobian matrix of V is evaluated at D_MS to give

()

The product of matrix F and V⁻¹ gives

()

Finding the eigenvalue of FV⁻¹, we obtain for the malaria-schistosomiasis coinfection model (12) is given by

()

Considering the parameters for our model from Table 1, the value of

appears to be far greater than 1. This implies that the disease (malaria-schistosomiasis coinfection model) will not die out but remains endemic in the population until some control strategies are applied properly. The disease-free equilibrium is locally stable if

. We can achieve the global stability for the disease-free equilibrium by following the Lyapunov argument for

. Hence, when the disease-free equilibrium is unstable, there exists an endemic equilibrium. Next we discuss the local stability of the disease-free equilibrium.

4.1. Local Stability of the Disease-Free Equilibrium of Malaria-Schistosomiasis Coinfection Model

The disease-free equilibrium for the malaria-schistosomiasis coinfection model given by = (b_H/d_H, 0,0, 0,0, 0,0, 0, b_s/d_s, 0, b_v/d_v, 0) exists for all values of d_H > 0, d_s > 0, and d_v > 0. If the threshold value is , then the disease-free equilibrium is locally asymptotically stable and the disease cannot invade or spread in the population or community. The summary of the result is given by Theorem 5.

Theorem 5. The disease-free equilibrium point D_MS is locally asymptotically stable if and unstable if .

It means that the malaria-schistosomiasis coinfection can be eliminated from the population whenever

; then, averagely an infected person produces less than one newly infected person over the entire period of his infectiousness and malaria-schistosomiasis coinfection dies out. For

to be less than one, the β₁, β₂, β₃, and β₄ (rates of transmission) must decrease without bounds. Otherwise, if

, then each infected person produces less, averagely more than one new infection, and the malaria-schistosomiasis coinfection can spread or invade the population. Consider the model equation (12). At the equilibrium state D_MS, the Jacobian is given by

()

where m₁ = β₂b_H/d_H, m₂ = β₁ϵ_hσb_H/d_H, m₃ = β₃b_s/d_s, m₄ = β₃η₁b_s/d_s, m₅ = β₄ϵ_vσb_v/d_v, m₆ = β₄ϵ_vση₂b_v/d_v, m₇ = (ω + d_H + θ), m₈ = (d_H + ρ_H + q_H), m₉ = (α + r + m + d_H), and m₁₀ = (g + d_H) + (1 − ϕ)(1 − α).

The local stability of D_MS is determined by the signs of the eigenvalues of the Jacobian matrix (65). The disease-free equilibrium point, D_MS, is said to be locally asymptotically stable if the real parts of the eigenvalues of the Jacobian matrix (65) are all negative; otherwise it is said to be unstable. By considering the Jacobian matrix (65), we obtain

()

The remaining characteristic polynomial corresponding to

()

where

()

The Routh-Hurwitz conditions to establish that all roots of (F₁) have negative real parts are A₁ > 0, A₂ > 0, A₃ > 0, and A₁A₂ > A₃. Note that all model parameters are positive. For A₃ to be positive set

()

which implies that

()

This leads to

()

which is true. Thus, by the Routh-Hurwitz condition, all the eigenvalues have negative real parts whenever R_M1 < 1, such that D_MS is locally asymptotically stable. F₂(λ) = λ² + (d_s + ρ_s + d_H + ρ_H + q_H)λ − β₃b_sβ₂b_H/d_sd_H + (d_s + ρ_s)(d_H + ρ_H + q_H), where

()

The Routh-Hurwitz conditions to make certain that all roots of (F₂) have negative real parts are E₁ > 0, E₂ > 0, E₃ > 0, and E₁E₂ > E₃. Note that all model parameters are positive. For E₃ to be positive set

()

which implies that

()

This leads to

. It can be verified that E₁E₂ − E₃ > 0; that is,

()

hence it is true. Accordingly, by the Routh-Hurwitz criteria, all the eigenvalues have negative real parts whenever R_S1 < 1, such that D_MS is locally asymptotically stable.

4.2. Impact of Schistosomiasis on Malaria and Vice Versa

The impact of schistosomiasis on malaria and vice versa can be analysed by expressing R_0m in terms of R_0s. We solve d_H to obtain the following.

Suppose

()

∴

()

Let

()

Therefore

()

Hence

()

We substitute d_H in R_0m to obtain

()

≥

is strictly positive, then the malaria enhances schistosomiasis infection. This means that whenever (85) is greater than zero, an increase in schistosomiasis will result in an increase of malaria cases in the community. If (85) is equal to zero, it implies that schistosomiasis cases will have no significant impact on the transmission dynamics of malaria. Accordingly, by expressing d_H in terms of R_0M (impact of malaria on schistosomiasis)

()

where

()

By assigning

()

therefore

()

By differentiating R_0S partially with respect to R_0M we obtain

()

If (90) is greater than zero, it means that an increase in the malaria accounts for an increase of schistosomiasis cases in the population. The impact of malaria treatment on schistosomiasis is evaluated by partially differentiating R_0M with respect to ω. We obtain ∂R_0M/∂ω = −1/(θ + ω + d_H). Since R_0M is a decreasing function of ω, the treatment of schistosomiasis will have a positive impact on the dynamics of malaria.

5. Sensitivity Analysis of the Malaria-Schistosomiasis Coinfection Model

Sensitivity analysis is the study of how the uncertainty in the output of a mathematical model or system can be distributed to different sources of uncertainty in its outputs. It is a scientific procedure used in determining how different values of an independent variable will affect a particular dependent variable under a given set of hypotheses. This method is applied within certain limits that will depend on more input variables. The sensitivity index is a measure of the relative change in a variable with respect to the relative change in its parameters. It is known that there are uncertainties which are associated with the estimation of certain parameter values. So, it will be useful to study the effect of these parameters on the basic reproduction number . The understanding from this study will help us to identify those parameters that cause the most increase/decrease in and by this we will be able to recognize the type of control measure(s) that is most suitable and effective in controlling the disease. Hence, we compute the normalized forward sensitivity index of with respect to the parameters in the model equation (12).

The normalized forward sensitivity index of a variable, u, that depends differentiably on index of a parameter, z, is defined as . As we have an implicit formula for we derive analytically for the sensitivity of as to each parameter involved in .

Important indices are given thus:

()

5.1. Interpretation of Sensitivity Indices

It is observed that the positive signs of sensitivity indices of the basic reproduction number to the model parameters reveal that an increase or reduction in the value of each of the parameter in this case will point to an increase or decrease in the basic reproduction number of the disease [22]. The case of the shows that increasing or reducing the mosquito biting rate by 10 percent increases or reduces the basic reproduction number, , by 10 percent. However, the negative signs of the sensitivity indices of the basic reproduction number to the model parameters show that an increase or reduction in the value of each of the parameter in this class indicates a corresponding reduction or increase in the basic reproduction number of the disease [22]. Hence, the sensitivity analysis of the malaria-schistosomiasis coinfection model (12) provides an effective means of knowing how the dynamics of the coinfection model respond to changes in parameters of the model [22]. More importantly, it helps as a guide to policy makers and public health authorities in focusing on an appropriate intervention strategy for preventing and controlling the spread of the disease. The sensitivity analysis is applied to study the relative importance of model parameters to malaria-schistosomiasis coinfection. The sensitivity analysis reveals how each parameters influence the malaria-schistosomiasis coinfection output. However, the analysis will be carried out with response to the most crucial and sensitive parameters to the malaria-schistosomiasis coinfection model.

6. Numerical Simulation and Graphical Illustration of the Malaria-Schistosomiasis Coinfection Model

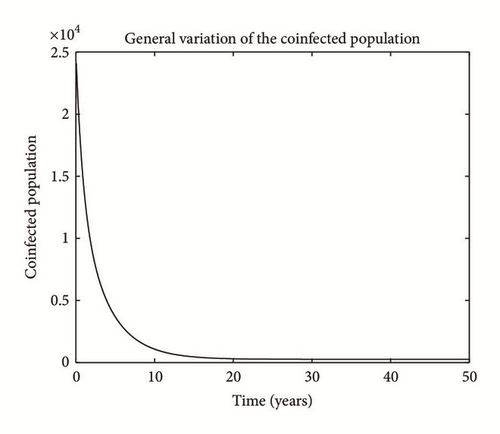
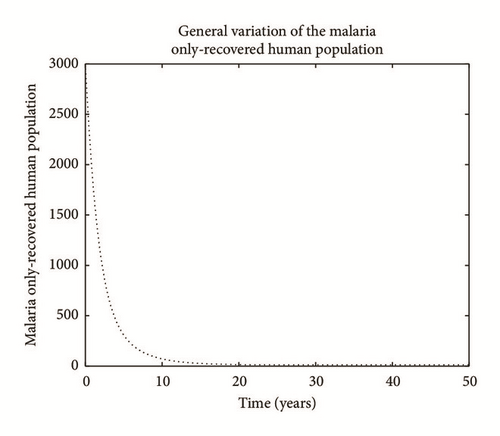
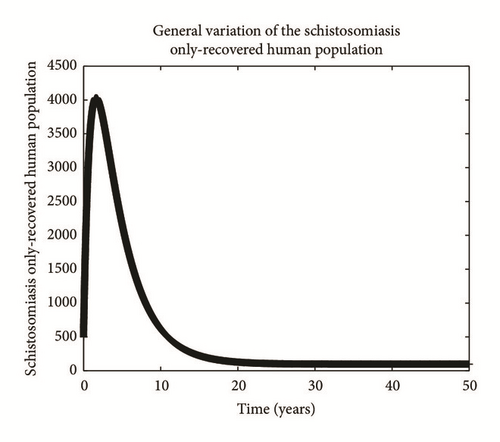
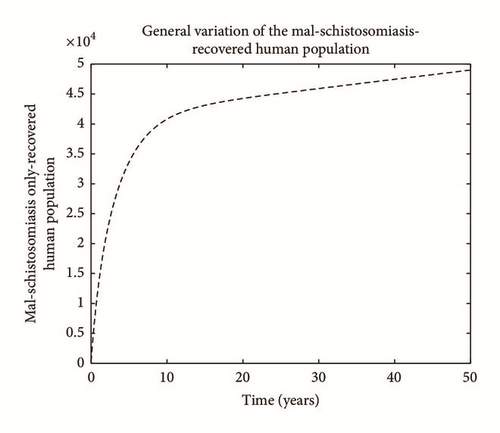
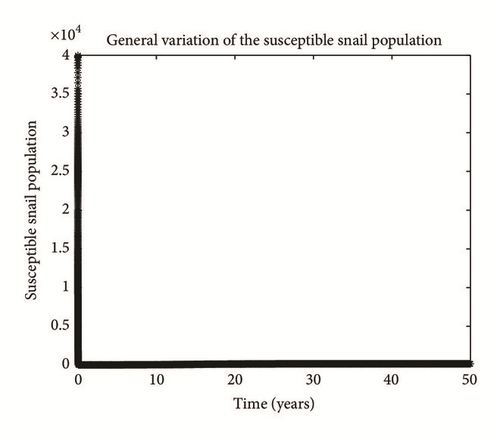
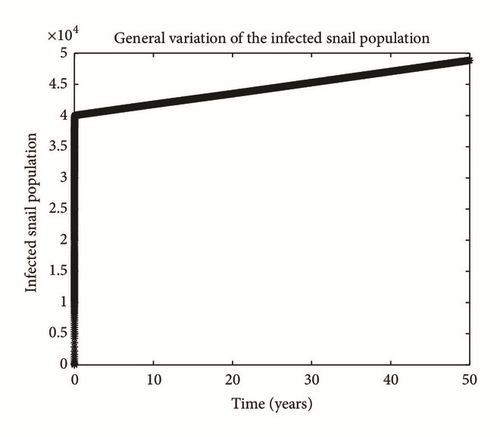
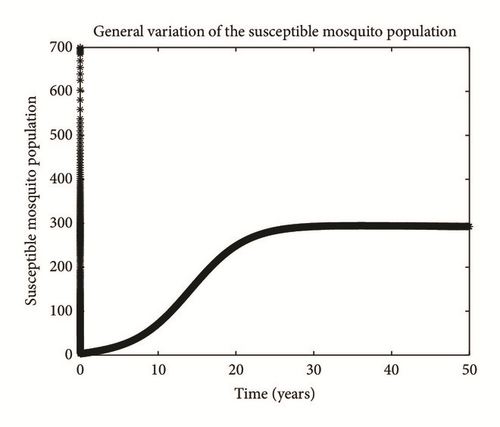
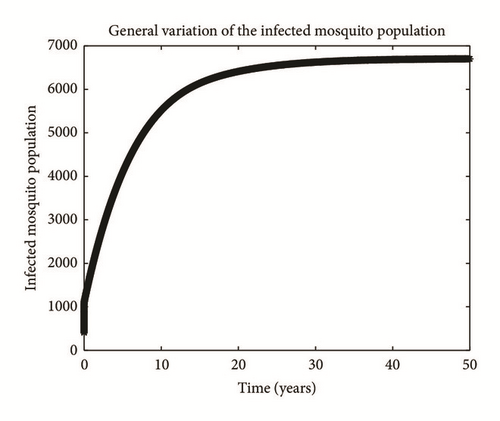
Numerical simulation and graphical illustrations are carried out in order to verify some of the analytical results. Different initial starts have been used from Table 2 to perform the computer simulations for different cases and displayed graphically in Figures 1–4. Figure 1 shows the variation of susceptible human (S_h), infected human with malaria only (I_m), infected human with schistosomiasis only (I_hs), and humans infected with both malaria and schistosomiasis (V_ms). It is observed that, in Figure 1(a), the susceptible human population decreases with time due to the malaria-schistosomiasis coinfections and in Figure 1(b), the population of malaria-infected human decreases with time due to treatment of the infected population. In Figure 1(c), the population of the schistosomiasis-infected human population also decreases due to the treatment while the population of the coinfected decreases to a particular level and then reaches its equilibrium point due to treatments. Figure 2 shows the variation of humans who recovered from malaria only (R_m), humans who recovered from schistosomiasis only (R_hs), and humans who recovered from both malaria and schistosomiasis (R_ms). It is observed that, in Figure 2(a), the population of malaria-recovered human population decreases with time to a level and in Figure 2(b), the population of the schistosomiasis-only-recovered human population increases with time and then decreases with time until it reaches its equilibrium point while, in Figure 2(c), the population of malaria-schistosomiasis recovered human population increases with time and then reaches its equilibrium point. Figure 3 shows the variation of susceptible mosquito (S_v) and infected mosquito with malaria (I_v). It is observed that, in Figure 3(a), the susceptible snail population decreases with time due to infection with schistosomiasis while, in Figure 3(b), the population of the infected snail maintains a constant equilibrium and then increases with time. Figure 4 shows the variation of susceptible mosquito (S_v) and infected mosquito with malaria (I_v). It is observed that, in Figure 4(a), the population of susceptible mosquito decreases and then increases to maintain a steady state while the infected mosquito population increases with time because of the presence of the infection.

Table 2. Table showing numerical values of parameters used in the model.

Parameter	Symbol	Value	Source
Disease induced death rate due to malaria only	θ	0.05	[23]
Probability of human getting infected with malaria	β₁	0.8333	[24, 25]
Rate of acquiring schistosomiasis through contact with infected snails	β₂	0.406	[26]
Rate of acquiring schistosomiasis through contacts with infected humans	β₃	0.0004	[26]
Probability of mosquito getting infected by an infectious human	β₄	0.09	[24, 25]
Malaria schistosomiasis immunity waning rate	φ	0.0005	[24]
Schistosomiasis induced death rate	r	0.02	[assumed]
Malaria disease induced death rate	m	0.06	[assumed]
Coinfected population who recovered from malaria only	ϕ	0.12	[assumed]
Disease induced death rate of human due to schistosomiasis only	ρ_H	0.0039	[27]
Disease induced death rate of snails due to schistosomiasis only	ρ_s	0.0004012	[28]
Human spontaneous recovery	ω	0.005	[13]
Rate of loss of immunity to the schistosomiasis disease only	k	0.7	[assumed]
Rate of loss of immunity to malaria and schistosomiasis disease	φ	0.0005	[24, 25]
Human spontaneous recovery from schistosomiasis only	q_H	0.56	[assumed]
Recovery rate of coinfected individual	α	0.7	[assumed]
Modification parameter	η₁	1.3	[assumed]
Modification parameter	η₂	1.4	[assumed]
Per capita birth rate of mosquitoes	b_v	1000	[24, 29]
Per capita birth rate of snails	b_s	200	[8]
Natural death rate of humans	d_H	0.00004	[10]
Per capita biting rate of mosquitoes	ϵ_v	0.2	[30–32]
Contact rate of vector per human per unit time	σ	0.502	[33]
Per capita biting rate of humans	ϵ_h	0.2	[30, 34]
Natural death rate of mosquitoes	d_v	0.1429	[24]
Natural death rate of snails	d_s	0.0000569	[26]
Rate of loss of immunity to the malaria disease only	γ	0.7902	[24, 29, 35]
Per capita birth rate of humans	b_h	100	[36]

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Simulation showing the variation of susceptible human (S_h) in (a), infected human with malaria only (I_m) in (b), infected human with schistosomiasis only (I_hs) in (c), and humans infected with both malaria and schistosomiasis (V_ms) in (d).

7. Concluding Remarks

In this paper, we developed and analysed a deterministic model for the transmission of malaria-schistosomiasis coinfection without intervention strategies. The model was rigorously analysed to gain insights into its qualitative dynamics. We obtained the following results: (i) the malaria-schistosomiasis coinfection model has a locally stable disease-free equilibrium whenever the associated reproduction number is less than unity. (ii) We observed from our analysis of the effect of schistosomiasis on malaria that schistosomiasis infection may be associated with an increased risk of malaria. (iii) We show that the interaction between schistosomiasis and malaria may reduce the effectiveness of malaria treatment for controlling malaria transmission. Sensitivity analysis of the reproduction number to the model parameter was performed to investigate the parameters that possess greater influence on the model. Sensitivity analysis also showed that mosquito biting rate ϵ_v and rate of acquiring schistosomiasis through contacts with infected snails β₃ among other parameters contribute most significantly to the transmission and spread of the malaria disease. Hence the intervention strategy that inhibits the human-mosquito contact and human-snail contact should be encouraged in order to achieve a malaria-schistosomiasis-free population.

Competing Interests

The authors declare that they have no competing interests.

References

1 Sambo L. G., Ki-Zerbo G., and Kirigia J. M., Malaria control in the African Region: perceptions and viewspoints on proceedings of the Africa Leaders Malaria Alliance (ALMA), BMC Proceedings. (2011) 5, no. supplement 5, article S3.
10.1186/1753-6561-5-S5-S3
Google Scholar
2 Su Z., Segura M., Morgan K., Loredo-Osti J. C., and Stevenson M. M., Impairment of protective immunity to blood-stage malaria by concurrent nematode infection, Infection and Immunity. (2005) 73, no. 6, 3531–3539, https://doi.org/10.1128/iai.73.6.3531-3539.2005.
10.1128/IAI.73.6.3531-3539.2005
CAS PubMed Web of Science® Google Scholar
3 Hurlimann E., Schur N., Boutsika K. et al., Toward an open-access global database for mapping, control, and surveillance of neglected tropical diseases, PLoS Neglected Tropical Diseases. (2011) 5, no. 12, e1404, https://doi.org/10.1371/journal.pntd.0001404.
10.1371/journal.pntd.0001404
PubMed Web of Science® Google Scholar
4 W.H.O., Global Malaria Programme: Position Statement on ITNs, 2009.
Google Scholar
5 Bakare E. A. and Nwozo C. R., Effect of control strategies on the optimal control analysis of a host-vector model for malaria under the inuence of infective immigrants, International Journal of Mathematics and Computations. (2015) 26, no. 1, 51–73, http://www.ceser.in/ceserp/index.php/ijmc.
Google Scholar
6 Alifrangis M., Lemnge M. M., Moon R., Theisen M., Bygbjerg I., Ridley R. G., and Jakobsen P. H., IgG reactivities against recombinant Rhoptry-Associated Protein-1 (rRAP-1) are associated with mixed Plasmodium infections and protection against disease in Tanzanian children, Parasitology. (1999) 119, no. 4, 337–342, 10581610, https://doi.org/10.1017/S0031182099004825, 2-s2.0-0032858727, 10581610.
10.1017/S0031182099004825
CAS PubMed Web of Science® Google Scholar
7 Bakare E. A., On the Qualitative behaviour of a human-mosquito model for Malaria with multiple vector control strategies, International Journal of Ecological Economics and Statistics. (2015) 36, no. 1, 96–113.
Google Scholar
8 Chiyaka E. T. and Garira W., Mathematical analysis of the transmission dynamics of schistoso-miasis in the human-snail hosts, Journal of Biological Systems. (2009) 17, no. 3, 397–423, https://doi.org/10.1142/s0218339009002910, MR2604374, 2-s2.0-69049089967.
10.1142/S0218339009002910
Web of Science® Google Scholar
9 Ross A. G. P., Bartley P. B., Sleigh A. C., Olds G. R., Li Y., Williams G. M., and McManus D. P., Schistosomiasis, The New England Journal of Medicine. (2002) 346, no. 16, 1212–1220, https://doi.org/10.1056/nejmra012396, 2-s2.0-0037129443.
10.1056/NEJMra012396
PubMed Web of Science® Google Scholar
10 Yang H. M., A mathematical model for malaria transmission relating global warming and local socioeconomic conditions, Revista de Saude Publica. (2001) 35, no. 3, 224–231, https://doi.org/10.1590/s0034-89102001000300002, 2-s2.0-0035376473.
10.1590/S0034-89102001000300002
CAS PubMed Web of Science® Google Scholar
11 King C. H. and Dangerfield-Cha M., The unacknowledged impact of chronic schistosomiasis, Chronic Illness. (2008) 4, no. 1, 65–79, https://doi.org/10.1177/1742395307084407, 2-s2.0-40349085389.
10.1177/1742395307084407
PubMed Google Scholar
12 WHO, Schistosomiasis (2001), 2007, http://www.who.int/mediacentre/factsheets/fs115.
Google Scholar
13 Chiyaka C., Tchuenche J. M., Garira W., and Dube S., A mathematical analysis of the effects of control strategies on the transmission dynamics of malaria, Applied Mathematics and Computation. (2008) 195, no. 2, 641–662, https://doi.org/10.1016/j.amc.2007.05.016, MR2381245, 2-s2.0-37349003324.
10.1016/j.amc.2007.05.016
Web of Science® Google Scholar
14 Hotez P. J., Molyneux D. H., Fenwick A., Ottesen E., Ehrlich Sachs S., and Sachs J. D., Incorporating a rapid-impact package for neglected tropical diseases with programs for HIV/AIDS, tuberculosis, and malaria, PLoS Medicine. (2006) 3, no. 5, article e102, https://doi.org/10.1371/journal.pmed.0030102.
10.1371/journal.pmed.0030102
PubMed Web of Science® Google Scholar
15 Sangweme D. T., Midzi N., Zinyowera-Mutapuri S., Mduluza T., Diener-West M., and Kumar N., Impact of schistosome infection on Plasmodium falciparum malariometric indices and immune correlates in school age children in Burma Valley, Zimbabwe, PLoS Neglected Tropical Diseases. (2010) 4, no. 11, article e882, https://doi.org/10.1371/journal.pntd.0000882, 2-s2.0-78649778495.
10.1371/journal.pntd.0000882
PubMed Web of Science® Google Scholar
16 Nacher M., Interactions between worms and malaria: good worms or bad worms?, Malaria Journal. (2011) 10, article 259, https://doi.org/10.1186/1475-2875-10-259.
10.1186/1475-2875-10-259
Web of Science® Google Scholar
17 Hartgers F. C., Obeng B. B., Kruize Y. C. M., Dijkhuis A., McCall M., Sauerwein R. W., Luty A. J. F., Boakye D. A., and Yazdanbakhsh M., Responses to malarial antigens are altered in helminth-infected children, Journal of Infectious Diseases. (2009) 199, no. 10, 1528–1535, https://doi.org/10.1086/598687, 2-s2.0-65549123258.
10.1086/598687
CAS PubMed Web of Science® Google Scholar
18 Helmby H., Kullberg M., and Troye-Blomberg M., Altered immune responses in mice with concomitant Schistosoma mansoni and Plasmodium chabaudi infections, Infection and Immunity. (1998) 66, no. 11, 5167–5174, http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=108644&tool=pmcentrez&rendertype=abstract.
10.1128/IAI.66.11.5167-5174.1998
CAS PubMed Web of Science® Google Scholar
19 Sokhna C., Hesran J.-Y. L., Mbaye P. A. et al., Increase of malaria attacks among children presenting concomitant infection by Schistosoma mansoni in Senegal, Malaria Journal. (2004) 3, article 43, https://doi.org/10.1186/1475-2875-3-43.
10.1186/1475-2875-3-43
Web of Science® Google Scholar
20 Ndeffo Mbah M. L., Skrip L., Greenhalgh S., Hotez P., and Galvani A. P., Impact of Schistosoma mansoni on malaria transmission in Sub-Saharan Africa, PLoS Neglected Tropical Diseases. (2014) 8, no. 10, e3234, https://doi.org/10.1371/journal.pntd.0003234, 2-s2.0-84920532208.
10.1371/journal.pntd.0003234
PubMed Web of Science® Google Scholar
21 Collins W. E. and Jeffery G. M., A retrospective examination of sporozoite- and trophozoite-induced infections with Plasmodium falciparum in patients previously infected with heterologous species of Plasmodium: effect on development of parasitologic and clinical immunity, The American Journal of Tropical Medicine and Hygiene. (1999) 61, no. supplement 1, 36–43, https://doi.org/10.4269/tropmed.1999.61-036, 2-s2.0-0032811835.
10.4269/tropmed.1999.61-036
CAS PubMed Web of Science® Google Scholar
22 Olaniyi S. and Obabiyi O. S., Quantitative analysis of malaria dynamics with nonlinear incidence function, Applied Mathematical Sciences. (2014) 8, no. 78, 3889–3904, https://doi.org/10.12988/ams.2014.45326.
10.12988/ams.2014.45326
Google Scholar
23 Smith? R. J. and Hove-Musekwa S. D., Determining effective spraying periods to control malaria via indoor residual spraying in Sub-Saharan Africa, Journal of Applied Mathematics and Decision Sciences. (2008) 2008, 19, 745463, https://doi.org/10.1155/2008/745463, 2-s2.0-53849118810.
10.1155/2008/745463
Google Scholar
24 Flahault A., Le Menach A., McKenzie E. F., and Smith D. L., The unexpected importance of mosquito oviposition behaviour for malaria: non-productive larval habitats can be sources for malaria trans-mission, Malaria Journal. (2005) 4, article 23, https://doi.org/10.1186/1475-2875-4-23.
10.1186/1475-2875-4-23
Web of Science® Google Scholar
25 Smith D. L. and McKenzie F. E., Statics and dynamics of malaria infection in Anopheles mosquitoes, Malaria Journal. (2004) 3, article 13, https://doi.org/10.1186/1475-2875-3-13, 2-s2.0-4844221308.
10.1186/1475-2875-3-13
Web of Science® Google Scholar
26 Spear R. C., Hubbard A., Liang S., and Seto E., Disease transmission models for public health decision making: toward an approach for designing intervention strategies for Schistosomiasis japonica, Environmental Health Perspectives. (2002) 110, no. 9, 907–915.
10.1289/ehp.02110907
PubMed Web of Science® Google Scholar
27 Feng Z., Eppert A., Milner F. A., and Minchella D. J., Estimation of parameters governing the transmission dynamics of schistosomes, Applied Mathematics Letters. (2004) 17, no. 10, 1105–1112, https://doi.org/10.1016/j.aml.2004.02.002, MR2091843.
10.1016/j.aml.2004.02.002
Web of Science® Google Scholar
28 Mangal T. D., Paterson S., and Fenton A., Predicting the impact of long-term temperature changes on the epidemiology and control of schistosomiasis: a mechanistic model, PLoS ONE. (2008) 3, no. 1, e1438, https://doi.org/10.1371/journal.pone.0001438, 2-s2.0-39049106517.
10.1371/journal.pone.0001438
CAS PubMed Web of Science® Google Scholar
29 Anderson R. M. and May R. M., Infectious Diseases of Humans: Dynamics and Control, 1991, Oxford University Press, Oxford, UK.
10.1093/oso/9780198545996.001.0001
Google Scholar
30 Kawaguchi I., Sasaki A., and Mogi M., Combining zooprophylaxis and insecticide spraying: a malaria-control strategy limiting the development of insecticide resistance in vector mosquitoes, Proceedings of the Royal Society of London B: Biological Sciences. (2004) 271, no. 1536, 301–309, https://doi.org/10.1098/rspb.2003.2575, 2-s2.0-1042302717.
10.1098/rspb.2003.2575
Web of Science® Google Scholar
31 Gu W., Killeen G. F., Mbogo C. M., Regens J. L., Githure J. I., and Beier J. C., An individual-based model of Plasmodium falciparum malaria transmission on the coast of Kenya, Transactions of the Royal Society of Tropical Medicine and Hygiene. (2003) 97, no. 1, 43–50, https://doi.org/10.1016/s0035-9203(03)90018-6, 2-s2.0-0013232032.
10.1016/S0035-9203(03)90018-6
PubMed Web of Science® Google Scholar
32 Snow R. W. and Omumbo J., D. T. Jamison, R. G. Feachem, M. W. Makgoba et al., Malaria, Diseases and Mortality in Sub-Saharan Africa, 2006, The World Bank, Washington, DC, USA.
Google Scholar
33 Chitnis N., Cushing J. M., and Hyman J. M., Bifurcation analysis of a mathematical model for malaria transmission, SIAM Journal on Applied Mathematics. (2006) 67, no. 1, 24–45, https://doi.org/10.1137/050638941, 2-s2.0-33847746157.
10.1137/050638941
Web of Science® Google Scholar
34 Ariey F. and Robert V., The puzzling links between malaria transmission and drug resistance, Trends in Parasitology. (2003) 19, no. 4, 158–160, https://doi.org/10.1016/s1471-4922(03)00054-0, 2-s2.0-0037384811.
10.1016/S1471-4922(03)00054-0
PubMed Web of Science® Google Scholar
35 Ruiz D., Poveda G., Vélez I. D., Quiñones M. L., Rúa G. L., Velásquez L. E., and Zuluaga J. S., Modelling entomological-climatic interactions of Plasmodium falciparum malaria transmission in two Colombian endemic-regions: contributions to a national malaria early warning system, Malaria Journal. (2006) 5, article 66, https://doi.org/10.1186/1475-2875-5-66, 2-s2.0-33748780619.
10.1186/1475-2875-5-66
Web of Science® Google Scholar
36 UNICEF, WHO: Progress for Children: A World Fit for Children Statistical Review, 2007.
Google Scholar

Citing Literature

All articles

Mathematical Analysis of Malaria-Schistosomiasis Coinfection Model

Abstract

1. Introduction

2. Model Formulation

2.1. The Full Schistosomiasis-Malaria Coinfection Model

2.2. Qualitative Analysis of the Full Schistosomiasis-Malaria Coinfection Model

2.3. Positivity of the Solution

2.4. Boundedness of the Solution

2.5. Invariant Region

3. Existence of Steady States Solution

3.1. Existence of Disease-Free Equilibrium Point (DFE)

4. The Basic Reproduction Number

4.1. Local Stability of the Disease-Free Equilibrium of Malaria-Schistosomiasis Coinfection Model

4.2. Impact of Schistosomiasis on Malaria and Vice Versa

5. Sensitivity Analysis of the Malaria-Schistosomiasis Coinfection Model

5.1. Interpretation of Sensitivity Indices

6. Numerical Simulation and Graphical Illustration of the Malaria-Schistosomiasis Coinfection Model

7. Concluding Remarks

Competing Interests

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Mathematical Analysis of Malaria-Schistosomiasis Coinfection Model

Abstract

1. Introduction

2. Model Formulation

2.1. The Full Schistosomiasis-Malaria Coinfection Model

2.2. Qualitative Analysis of the Full Schistosomiasis-Malaria Coinfection Model

2.3. Positivity of the Solution

2.4. Boundedness of the Solution

2.5. Invariant Region

3. Existence of Steady States Solution

3.1. Existence of Disease-Free Equilibrium Point (DFE)

4. The Basic Reproduction Number

4.1. Local Stability of the Disease-Free Equilibrium of Malaria-Schistosomiasis Coinfection Model

4.2. Impact of Schistosomiasis on Malaria and Vice Versa

5. Sensitivity Analysis of the Malaria-Schistosomiasis Coinfection Model

5.1. Interpretation of Sensitivity Indices

6. Numerical Simulation and Graphical Illustration of the Malaria-Schistosomiasis Coinfection Model

7. Concluding Remarks

Competing Interests

References

Citing Literature

Figures

References

Related

Information