The primary current distribution and the resistance of a modified Hull cell are calculated by using conformal mapping technique coupled with numerical evaluation of the resulting integral equations. An approximate analytical expression for the primary current distribution of a modified Hull cell is presented. The primary current distribution along the cathode surface is noticed varying in controlled manner as a function of position on the substrate. The current distributions (primary, secondary, and tertiary) in the cell have also been calculated at different applied average current densities (2, 4.1, and 8.2 mA cm⁻²) through numerical simulation by using finite element based software. The numerical simulation result of the primary current distribution is then compared with the analytical solution and a good match is found. Experimentally, single Cu metal electrodeposition is carried out at different applied average current densities (2, 4.1, and 8.2 mA cm⁻²) in a modified Hull. The current distribution (primary, secondary, and tertiary) results obtained from the numerical simulation are compared with the experimental results and a satisfactory match is found. Surface morphology of the Cu deposits is examined using scanning electron microscopy (SEM).

1. Introduction

Electrodeposition, a versatile, cost effective, and simple technique, is used to fabricate metallic coatings. The electrodeposition process parameters especially current density can affect the surface morphologies, chemical compositions (in case of alloys), and properties of the coatings which is clearly described in many reports of the literature [1, 2]. Prior to electrodeposition of materials, the primary goal of the electroplaters as well as the researchers is to study the current density distribution over the electrode surface in the electrochemical cell during electrodeposition [3].

In electroplating, the given electrochemical cell configuration is first needed to be understood with calculation of the current density distribution in the cell by taking into account other effects such as electrochemical reaction kinetics and mass transfer. However, to analyze and understand the electrochemical system, the initial step is the calculation of primary current distribution (PCD) along the electrode surface and primary resistance of the electrochemical cell in which the surface overpotential is neglected and the equipotential surface of the solution adjacent to the electrode is assumed [4].

The primary current along the electrode and the potential distribution in the electrolyte are calculated from solution of Laplace’s equation (∇²ϕ_l = 0). In literature, many techniques are available to solve Laplace’s equation such as method of images [5, 6], separation of variables [7], superposition [8, 9], and conformal mapping [10–19]. The analytical solutions for the PCD for different geometries have been reviewed by Fleck [20], a long time ago. Among these techniques, conformal mapping is a powerful and simple technique used to solve Laplace’s equation for planar as well as complex geometries [21–23].

In the literature, many articles [10, 12, 13, 19] can be found on the calculation of PCD in the electrochemical cells using conformal mapping technique. In general also, introduction and applications of the conformal mapping and Schwartz-Christoffel transformation in the complex variables problems have been addressed in the textbooks [21–24].

Conformal mapping technique has long been used to calculate current distributions in different electrochemical cell geometries [10–19] and is explained below. This technique is first used by Moulton to determine current distribution in the rectangular conductors [10]. Orazem and Newman [4] studied the PCD and the resistance of slotted electrodes cell using Schwarz-Christoffel transformation coupled with the numerical integrals. The effect of small changes in the angle between the electrode and the insulator on the PCD for recessed electrodes has also been studied using conformal mapping technique [18]. Recently, in the article published by West et al. [19] the analytical solution of the PCD in Hull cell and related trapezoidal geometries is explored using Schwarz-Christoffel transformations.

Generally, COMSOL Multiphysics, a finite element based software, is used to study the current and the potential distribution along the cathode in several electrochemical cells [26–28]. In the literature, the mathematical models are developed to investigate single metal deposition in trapezoidal geometry Hull cell [3, 19, 29, 30]. In the present study, a modified Hull cell having similar trapezoidal geometry is used. The alloy thin film materials libraries have been fabricated in the modified Hull cell through electrodeposition [2, 31–33]. To understand the modified Hull cell structure, numerical simulation of current distribution along the electrode during Cu electrodeposition has been carried out using finite element based software.

Generally used pure Cu electrodeposition from acid sulfate electrolytes is considered to compare with the simulated results [3, 28, 34]. Unlike other Cu types of electrodeposition in the literature, in the present study pure Cu thin films are fabricated experimentally from citrate based electrolyte. There is limited number of articles available on electrodeposition of Cu from citrate electrolytes [35, 36]. Citrate is a complexing-buffering-leveling agent. Recently, Chassaing et al. [35] fabricated pure Cu films from the citrate electrolytes having different concentrations of citrate and developed a model to explain the effect of citrate concentration on the kinetics of Cu electrodeposition.

In the present work, the main objective is the calculation of the primary current distribution and primary resistance of the cell of the modified Hull cell using conformal mapping technique. The development of the analytical expression for the PCD and the calculation of primary cell resistance value using conformal mapping technique (Schwartz-Christoffel Transformations) are presented. Further, numerically current density distributions (PCD, secondary (SCD), and tertiary (TCD)) in the cell during Cu electrodeposition carried out at different applied average current densities are investigated and its PCD is compared with the analytical PCD curve. Finally, Cu is deposited experimentally through pulsed electrodeposition in a modified Hull cell at similar applied average current densities and its normalized thickness distributions is compared with the numerically simulated current distribution (PCD, SCD, and TCD) results.

2. Computational and Experimental Methods

2.1. Analytical Solution of PCD in the Modified Hull Cell

2.1.1. Description of Modified Hull Cell

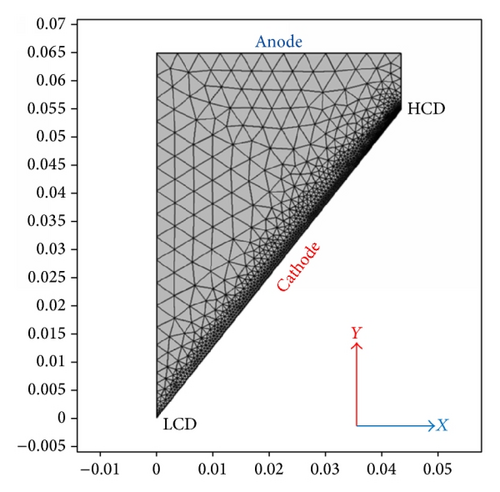
Modified Hull cell, a simple small electrodeposition cell, has a trapezoidal structure which consists of cathode (dimensions: 7 × 3.5 cm²) placed at an angle of 51.5° with anode (dimensions: 4.35 × 3.5 cm²) and two insulating walls (schematic diagram is shown in Figure 1). The closest (high current density (HCD) end) and farthest (low current density (LCD) end) distances between the electrodes are kept at 1 cm and 6.5 cm, respectively. The current density gradient is established along the length of the angled working electrode due to the geometry of the electrodes in the modified Hull cell where it is increased from LCD end to HCD end of the working electrode. This allows researchers to study the effect of wide range of current densities on the quality of the coating in a single experiment. Therefore, the study of the current distribution in the cell is of prime importance in the electrodeposition technique, mainly to determine the optimal plating conditions in practice.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Schematic diagram of the modified Hull cell geometry.

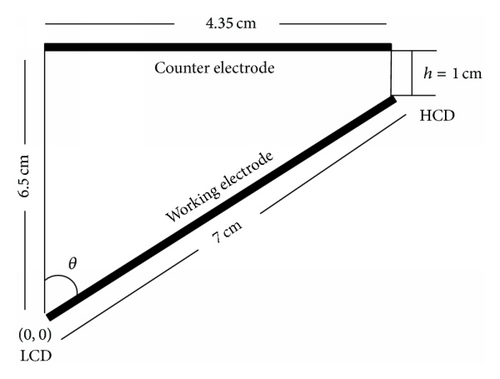
2.1.2. Calculation of PCD in the Modified Hull Cell

In contrast to standard Hull cell geometry, a modified Hull cell with an angle between the electrodes of 51.5° and modified dimensions of anode and cathode is designed to fabricate the Cu films in the present study. As stated in the introduction, the study of current distribution in a designed modified Hull cell is of prime concern and is necessary to be known before electrodeposition of metals.

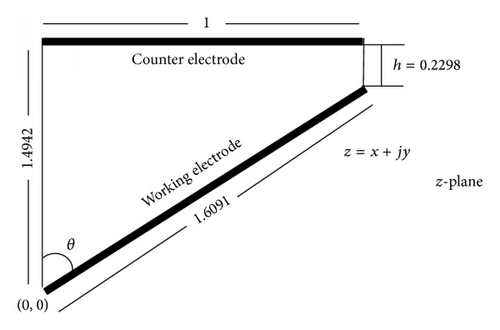
The dimensions of the modified Hull cell before and after scaling are shown in Figures 1 and 2(a). The scaling has been done with the anode length. The equations used to obtain the analytical solution of PCD in the modified Hull cell involve dimensionless quantities. Therefore, scaling of the modified Hull cell geometry dimensions must also be performed to generate the dimensionless quantities.

The conformal mapping technique is a powerful tool and is used to obtain analytical solution of PCD of a modified Hull cell. The actual cell geometry, the trapezoid (z-plane, Figure 2(a)), is mapped by two Schwartz-Christoffel transformations ((1) and (2)) into the rectangle (χ-plane, Figure 2(c)) through intermediate coordinate system (w-plane, Figure 2(b)). The current and the potential distributions for the rectangle geometry are determined simply from the solution of the differential equations with the boundary conditions (a and b) and then the solution is connected back to the actual cell geometry using Schwartz-Christoffel transformations which is already explained in detail in these references [4, 18, 19]:

()

Boundary conditions are as follows:

(a)
when w = 1, (x, y) = (1, cot θ) and when w = 1 + c, (x, y) = (1, h + cot θ) (for determination of the constants K₁ and c from (1));
(b)
when w = 1, (χ_r, χ_i) = (1,0) (for determination of the constants K₂ from (2)).

2.2. Numerical Simulation of Cu Electrodeposition

Though Cu films are fabricated experimentally through pulsed electrodeposition in a modified Hull cell, the average current densities used in the experimental PED are only used in the simulation of current distributions during Cu electrodeposition.

2.2.1. Geometry of the Modified Hull Cell

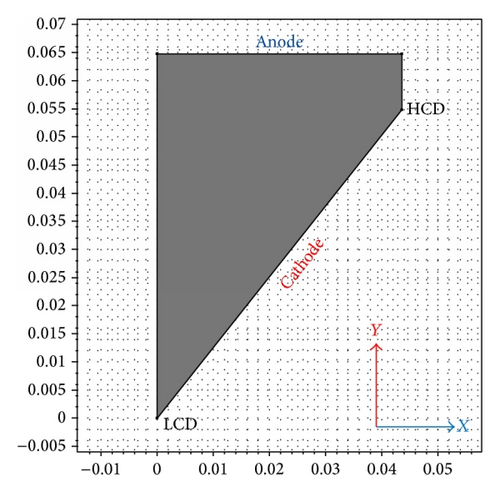
Figure 3 shows the 2D geometry used in the numerical simulation which consists of inclined cathode and horizontal anode and two vertical insulating walls.

2.2.2. Theoretical Development

In the absence of the concentration gradients in the electrolyte, Ohm’s law offers the relationship between local current density (i_l) at any point in the modified Hull cell and local potential derivative (∇ϕ_l) and is given by

()

where κ denotes the conductivity of the electrolyte.

The potential distribution in the electrolyte is calculated from the solution of Laplace’s equation:

()

In the absence of kinetic resistance and mass transfer effects, the current distribution resulted from ohmic resistance of the electrolyte or the geometry of the electrolytic cell called primary current distribution (PCD) that is assessed by applying the following boundary conditions along the cathode, the anode, and the insulating walls:

()

where i_avg is the applied average current density and ξ is the normal to the cathode surface.

By neglecting the concentration effects within the diffusion layer, the current distribution resulted from both effects such as the reaction kinetics on electrode and the geometry of the cell called secondary current distribution (SCD). The formation of different electroactive species with Cu²⁺ ions from citrate baths depending on the plating bath parameters such as solution pH and total citrate concentration is described in detail elsewhere [40]. In the present simulation study, only pure Cu²⁺ ions are considered because numerical solution is not achieved with the finite element based software when Cu citrate complex (Cucit⁻) singly and both the combination of Cu²⁺ and Cu citrate complex (Cucit⁻) are taken into consideration. Hence, the following Cu deposition reactions (j) (6) is assumed taking place on the cathode and its surface kinetics is described by cathodic Tafel expression (7). One has

()

where i_j is the partial current density due to electrode reaction j, i_0,j is the exchange current density at bulk concentrations for reaction, j and α_c,j are cathodic transfer coefficient of reaction, j.

The following equation is used to calculate the overpotential (η_j) for the electrode reaction, j:

()

where ϕ_s,0 is the electric potential of the metal, ϕ_l is the electrolyte potential, and V_Eq,j is the equilibrium potential.

Equilibrium potential for Cu electrode reaction j is calculated according to the following equation:

()

where

is standard reduction potential of Cu electrode reaction j (i.e., +0.34 V versus NHE).

When geometry effect, electrode kinetics effect, and concentration effects within the diffusion layer are considered, the resulted current distribution is called tertiary. Nernst diffusion layer model is used and is assumed to be constant thickness of 30 μm for the diffusion layer along the working electrode. Diffusion layer is a stagnant layer located very close to the working electrode surface. Inside this layer, only the varying concentration of metal ions is considered and the convection along the inclined working electrode is neglected. The contribution from the migration of mass transport limited specie, that is, Cu²⁺, is small and its effect is also neglected. Therefore, the mass transport mechanism of electroactive species within the diffusion layer is described by diffusion only,

()

where c is the concentration at the surface of the working electrode, N is the flux of electroactive species (Cu²⁺), and D is the diffusion coefficient of electroactive species (Cu²⁺).

The concentration distribution within the diffusion layer is calculated by using Laplace’s equation:

()

The concentration at the interface between the diffusion layer and the bulk electrolyte is assumed to be constant and is set to the bulk concentration value (c^b):

()

The boundary conditions at insulating surfaces are given by

()

The modified Tafel cathodic expression is used to calculate the tertiary current distribution along the working electrode and is given by

()

where c and c^b are concentration of copper ions at electrode surface and in the bulk electrolyte. Mapped type of mesh is used in the diffusion layer and free triangular type of mesh is used in the remaining geometry of the modified Hull cell, as shown in Figure 4.

For numerical simulation of Cu electrodeposition using COMSOL, the Electrochemistry Module (primary (secondary) current distribution (siec) interface) is used to simulate PCD, SCD, and TCD. After calculating the PCD, current distribution is changed from primary to secondary in the Current Distribution Type section to solve the SCD. The combination of secondary current distribution (given as “siec” in COMSOL) and Transport of Diluted Species (given as “chds” in COMSOL) physics is used to calculate TCD and concentration distribution in the diffusion layer.

2.3. Experimental

2.3.1. Cu Electrodeposition

For Cu electrodeposition, stainless steel of 7 × 3.5 cm² and pure Cu (99.9%) of 4.35 × 3.5 cm² are used as the substrate and the anode materials, respectively. The substrate materials are polished mechanically to generate mirror like surface followed by ultrasonic cleaning in acetone for 5 min and rinsing with deionized water. The angle, closest distance, and farthest distance of the oblique angled cathode to vertically positioned anode in the modified Hull cell are 51.5° (approximately), 1 cm and 6.5 cm, respectively. Pulsed electrodeposition (PED) is used to fabricate pure Cu films onto stainless steel substrate in a modified Hull cell of 1 liter capacity plating bath composed of 0.02 M CuSO₄·5H₂O and 0.2 M Na₃C₆H₅O₇·2H₂O. The bath is operated at 55°C and the operating pH is 4. The agitation of the bath is maintained at 200 rpm through magnetic stirrer. The pulsed electrodeposition experiments are performed at on-time of 1 ms, off-time of 10 ms, and applied average current densities of 2 (applied current of 0.05 A), 4.1 (applied current of 0.1 A), and 8.2 mA cm⁻² (applied current of 0.2 A) for 60, 30, and 15 min, respectively.

2.3.2. Scanning Electron Microscopy (SEM)

The surface morphologies of the fabricated Cu films are investigated on Zeiss Supra field emission scanning electron microscope through secondary electron imaging operating at 10 kV of accelerating voltage.

2.3.3. Thickness Measurements with Optical Profiler

Thickness of the deposited films is measured with optical profiler (Zeta Optical Profiler-20). Thickness measurements are taken at a regular distance of 1 cm from LCD end to HCD end of the substrates. Thickness data at each position on the working electrode is the average of the four measurement points taken horizontally on both sides from the centre of the substrates.

2.3.4. Transport and Kinetic Parameters

The parameters (considered for the simulation which is listed in Table 1) used in the simulation are obtained from the previous experimental works [37–39].

Table 1. Transport and kinetic parameters used in the numerical simulation.

Parameter	Value	Reference
Electrolyte conductivity (S cm⁻¹)	0.5	Measured
Applied average current densities (i_app) (A cm⁻²)	−2, −4.1, and −8.2
Exchange current density (i₀) (A cm⁻²)	3.92 × 10⁻⁷	[37]
Tafel slope (β_c) (V)	−0.13	[38]
Diffusion coefficient (cm² s⁻¹)	1 × 10⁻⁵	[39]

The conductivity of the electrolyte (κ) is determined experimentally using Electrochemical Impedance Spectroscopy (EIS) technique, that is, 0.5 (S cm⁻¹).
T = 328 K.

3. Results and Discussion

3.1. Analytical Solution of PCD for Modified Hull Cell

The asymptotic or approximate solution for the analytical expression of the PCD in the trapezoidal geometry type electrochemical cells is presented in [19]. The constants in the Schwartz-Christoffel transformations (K₁, K₂, and c) are calculated using numerical procedure which is also explained elsewhere [19].

The parameters of the modified Hull cell are given in the following.

θ = 0.2139 π radians, h = 0.2298 (after scaling), K₁ = 0.3078, K₂ = 0.1677, and c = 0.0197.

The form of an estimation of current distribution in the modified Hull cell by substituting the calculated constants (K₁, K₂, and c) in the asymptotic solution is given by

()

The comparison of current density distribution in the modified Hull cell (15) with traditional Hull cell (16) [19] and an empirical formula (17) [25] is shown in Figure 5. One has

()

for 0.186 < x < 0.941.

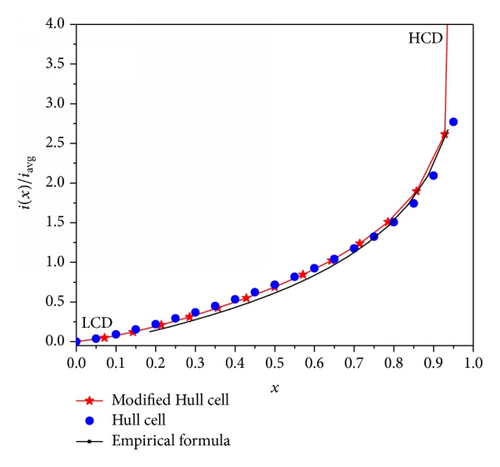
The PCDs obtained from (15), (16), and (17) are in a good agreement. From LCD end to near HCD end of the working electrode, the PCD of the modified Hull cell is following exactly the PCD of the Hull cell. But, near HCD end, it follows PCD calculated from an empirical formula.

3.2. Primary Resistance of the Modified Hull Cell

The dimensionless ohmic resistance (RκΔ) of the modified Hull cell (shown in Figure 2(a)) is calculated using

()

where Δ is the width of the modified Hull cell (perpendicular to the plane represented by Figure 2(a)), κ is the conductivity of the electrolyte, and R is the electrolyte resistance.

For modified Hull cell, the calculated dimensionless ohmic resistance is found equal to 0.5223.

3.3. Numerical Solution of Current Density Distributions (Primary, Secondary, and Tertiary) for Modified Hull Cell

3.3.1. Current Density Distribution Lines

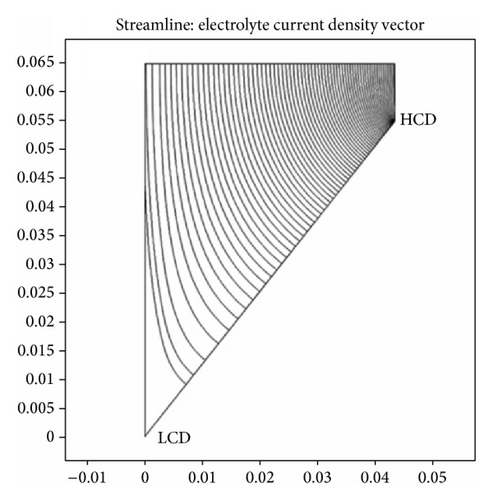
The current density distribution lines are drawn in the cell to confirm high and low values of current densities at HCD end and LCD end of the working electrode, as shown in Figure 6. At the HCD end, high density of current density distribution lines is found whereas low density is observed at the LCD end of the working electrode.

3.3.2. Primary Current Distribution

Figure 7 shows the normalized primary current distribution (i(x)/i_avg) calculated by finite element based software for different applied current densities: 2, 4.1, and 8.2 mA cm⁻² as a function of position on the working electrode. It is increasing from LCD end to HCD end of the working electrode as position on the working electrode increases but it is found constant for all applied average current densities: 2, 4.1, and 8.2 mA cm⁻². It confirms that PCD provides nonuniform distribution which covers wide range of current densities from LCD end to HCD end of the working electrode. Therefore, it gives a chance to study the influence of wide range of current densities on the characteristics of the deposit in a single experiment. From these results, the PCD dependence on the geometry of the cell itself is clearly known.

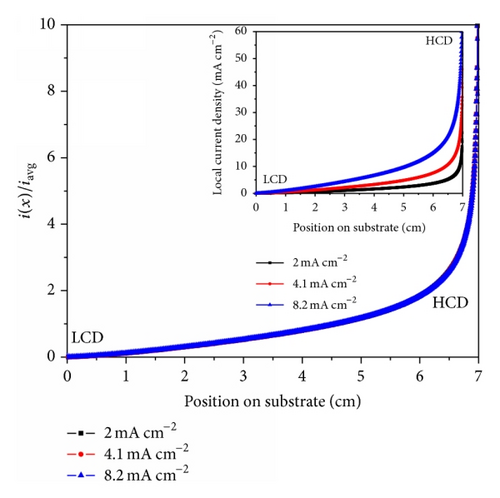
Inset figure in Figure 7 shows the local primary current densities that increases from LCD end to the HCD end of the working electrode and again increases with the increase of the applied current densities. Also, nonuniform nature of the primary current distribution is found to increase with increasing applied average current density.

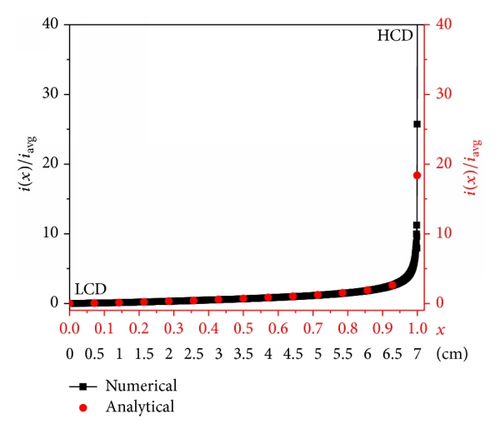
3.3.3. Comparison between Analytical and Numerical Simulation Solutions of PCD

Figure 8 shows the analytical solution (red color solid circular dots) of the PCD obtained from (15) along the inclined cathode of the modified Hull cell. The simulated PCD is also shown in Figure 8. Both analytical and numerical simulated primary current distributions are compared and are found in good agreement with each other. Note here that the dimensionless distance along the working electrode (x) used as x-axis in analytical calculations can also be replaced with dimensional distance (cm) used in the numerical simulation.

3.3.4. Secondary Current Density Distribution

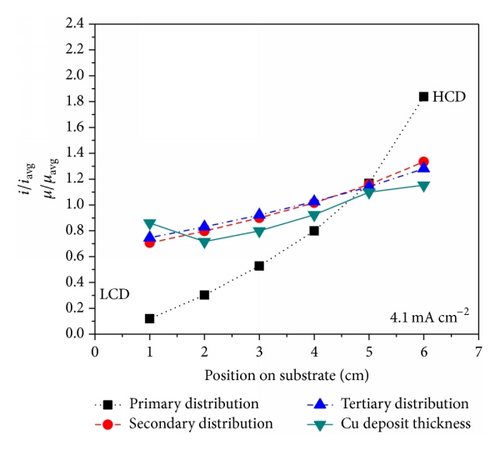
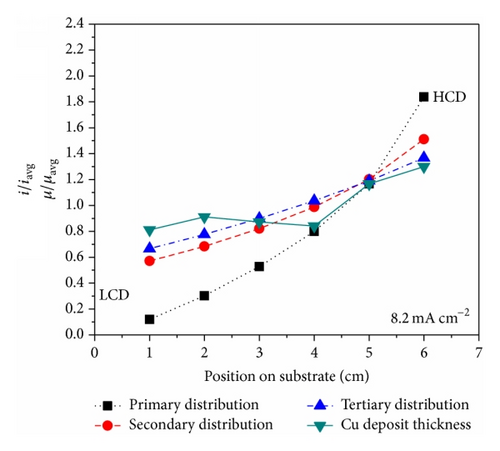
By adding the effect of electrode reaction kinetic resistance to PCD in the numerical simulation, the resulted secondary current distributions obtained for different applied average current densities, 2, 4.1, and 8.2 mA cm⁻², are shown in Figure 9. The normalized secondary current distribution is also found increasing from LCD end to HCD end of the working electrode. The dependence of uniformity of the secondary current density distribution on applied average current densities is clearly understood from Figure 9. It is observed that the current distribution is more uniform at 2 mA cm⁻² than that of 8.2 mA cm⁻². The nonuniformity of current distribution increases with increasing applied average current density in the case of SCD. Therefore, SCD becomes PCD at high applied average current density where the electrode reaction kinetics is very fast (approximately equal to infinity).

A single dimensionless parameter, the Wagner number (W_a), is used to express the significance of the SCD relative to the PCD and it represents the ratio between the polarization resistance at the deposition potential and the ohmic resistance in the electrolyte:

()

where L is the characteristic length of the system and κ is the conductivity of the electrolyte.

The equation related to the Wagner number evaluated at the Tafel limit is given by

()

where β_c is Tafel slope and i_avg is the applied average current density.

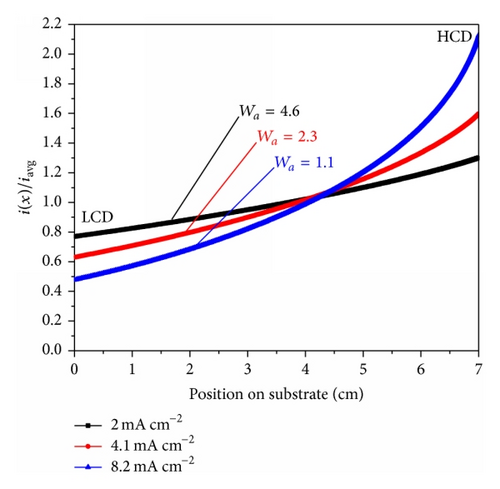
It is a measure of the uniformity of current distribution on the cathode. The most uniform current distribution resulted when the Wagner number reaches its highest value [41]. Therefore, Figure 9 reveals that the uniformity of the current density increases with increasing in the Wagner number from 1.1 (8.2 mA cm⁻²) to 4.6 (2 mA cm⁻²).

3.3.5. Tertiary Current Density Distribution

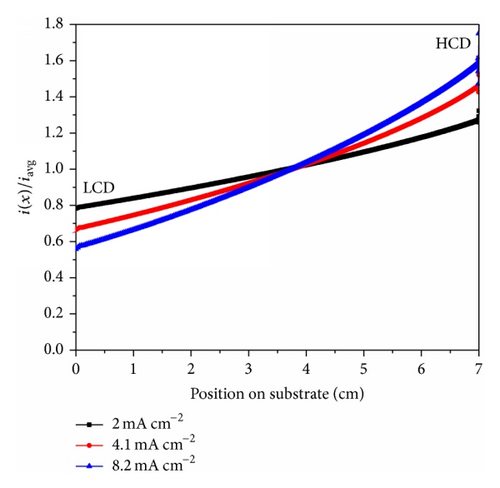
By the addition of concentration effects in the diffusion layer to other effects such as geometry and electrode reaction kinetic resistance in the numerical simulation, the resulted tertiary current distributions obtained for different applied average current densities, 2, 4.1, and 8.2 mA cm⁻², are shown in Figure 10. The shape and nature of the normalized tertiary current distribution are similar to those of SCD. However, compared to the SCD curves, the current density values are increasing at the LCD end and are decreasing at the HCD end of the working electrode as the applied average current density is increased from 2 to 8.2 mA cm⁻² because of the variation in the concentration of copper ions within the diffusion layer. These numerically calculated PCD, SCD, and TCD are then compared with the experimental data.

3.3.6. Comparison of Simulation and Experimental Values

To compare the simulated curves with the experimental results, Cu deposition from the citrate based plating bath is carried out at different average current densities: 2, 4.1, and 8.2 mA cm⁻² for 60, 30, and 15 min, respectively. The thickness of the deposit (μ) is calculated at a regular distance of 1 cm from the LCD end to the HCD end of the working electrode. The average deposit thickness (μ_avg) is calculated using Faraday’s law:

()

where M is the molar mass of Cu, i_avg is applied average current density, t is total deposition time, n_j is the number of electrons transferred in the electrode reaction, j, F is the Faraday constant, and ρ is density of Cu. The ratio (μ/μ_avg) (dimensionless Cu deposit thickness distribution) is calculated and is then compared with the normalized current distributions (primary, secondary, and tertiary) (i/i_avg), shown in Figure 11. The dimensionless deposit thickness distribution (μ/μ_avg) must be equal to the normalized current distribution (i/i_avg) in the case of 100% current efficiency.

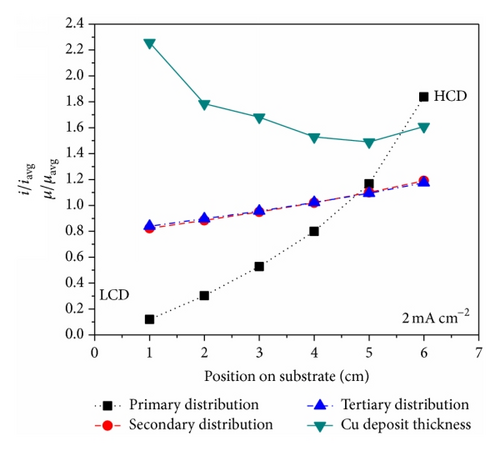
For the Cu film fabricated at 2 mA cm⁻² (see Figure 11(a)), the experimentally calculated deposit thickness distribution is uniform along the working electrode, except first measurement point in the LCD end, indicating that it follows the simulated SCD and TCD behavior. But it lies above the simulated SCD and TCD curves due to high average current efficiencies of 188.7%, as shown in Figure 12. The current efficiencies more than 100% are reported during Cu electrodeposition from citrate based electrolytes [35]. The measured weight of the deposit is higher than the theoretical weight due to the presence of organic inclusions in the deposit. The inclusion process is described in previous studies [35, 42–44]. It is assumed in [35] that the inclusion of cupric citrate complex type ions as a whole into film is comprised of complicated reactions in which the complexing agent might be broken down or chemically transformed before becoming inclusion in the deposit. In this study also, the authors suspect similar inclusion of organic products into the deposit which also might resulted into the reverse thickness distribution tendency observed in the Cu film fabricated at 2 mA cm⁻² (see Figure 11(a)).

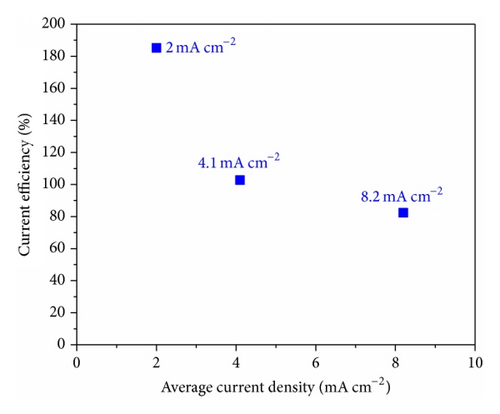
In case of Cu film fabricated at 4.1 mA cm⁻² (see Figure 11(b)), the experimentally calculated deposit thickness distribution curve lies slightly below the theoretical SCD and TCD curves though the average current efficiency in this experiment is little higher than 100% (~105%), as shown in Figure 12.

For the Cu film fabricated at 8.2 mA cm⁻² (see Figure 11(c)), the experimentally calculated deposit thickness distribution curve lies above the theoretical SCD and TCD curves as position is measured from 1 cm to 3 cm, follows the theoretical PCD curve from 4 cm to 5 cm, and follows theoretical TCD curve from 5 cm to 6 cm along the surface of the working electrode. The obtained average current efficiency is measured 84.5% which is lower than the theoretical 100%, as shown in Figure 12. Also it is noticed that while moving towards the HCD end from the middle point due to hydrogen gas evolution reaction, the measured thickness points are deviating from the numerically simulated SCD and TCD curves.

4. Surface Appearance and Morphological Analyses of Cu Films

The Cu films are fabricated through pulsed electrodeposition in a modified Hull cell for 60, 30, and 15 min at different applied average current densities 2, 4.1, and 8.2 mA cm⁻². It is observed that, at all applied average current densities of 2, 4.1, and 8.2 mA cm⁻², the deposit is bright throughout the coating surface over current density range of 1.1–5.2, 0.2–10.7, and 0.4–21.4 mA cm⁻² (current density at the both edges of the cathode is not considered). At an applied average current density of 2 mA cm⁻², the film is not formed completely at the center of the substrate in the current density range 0.1–1.1 mA cm⁻². The bubbles are observed at HCD end of the substrate in the Cu films fabricated at applied average current densities of 4.1 and 8.2 mA cm⁻². The reddish color of the deposit surface is changed from light to dark in 2 to 8.2 mA cm⁻².

The surface morphologies of Cu electrodeposits fabricated by pulsed electrodeposition from citrate-sulfate electrolyte at applied average current densities ≈2, 4.1, and 8.2 mA cm⁻² are investigated at different positions of the working electrode using SEM and are shown in Figures 13(a)–13(i), respectively. The distinctive changes in the surface morphology of Cu films taken at different regions on the substrate are observed due to variation in current densities. The surface morphology of the electrodeposited films depends on the electrode reaction mechanisms such as charge transfer and mass transport rates [45, 46].

The surface morphology of electrodeposited Cu in different applied average current densities (2 (a)–(c), 4.1 (d)–(f), and 8.2 mA cm⁻² (g)–(i)) is found varied from smooth to granular to globular with rough surface (because of hydrogen gas evolution), indicating mass transfer electrodeposition mechanism. It is expected that hydrogen gas evolution reaction consumes some portion of the applied currents which should result into low current efficiencies for Cu electrodeposition carried out at applied average current densities of 4.1 and 8.2 mA cm⁻².

5. Summary

(i)
Analytical calculation of primary current distribution and primary cell resistance of the modified electrochemical Hull cell is performed using conformal mapping technique. The analytical solution of PCD of the modified Hull cell is then compared with the standard Hull cell and the empirical formula and a good agreement is found.
(ii)
Numerical simulation of current distributions (primary, secondary, and tertiary) during the electrodeposition of Cu is carried out at different applied current densities: 2, 4.1, and 8.2 mA cm⁻² in a modified Hull cell using COMSOL Multiphysics software.
(iii)
For comparison, Cu film with thickness gradient is fabricated through pulsed electrodeposition in a modified Hull in a single experiment from the citrate based electrolyte.
(iv)
For Cu electrodeposition, the experimentally measured normalized thickness distribution (μ/μ_avg) is compared with the numerically calculated PCD, SCD, and TCD obtained at different applied average current densities 2, 4.1, and 8.2 mA cm⁻². At 2 mA cm⁻², higher experimental thickness distribution of Cu deposit is observed which might be due to organic inclusions increasing its weight, whereas, in case of the Cu film fabricated at 4.1 mA cm⁻², the experimental thickness distribution almost corresponds similar to the simulated SCD and TCD curves. For the Cu film fabricated at 8.2 mA cm⁻², the experimental thickness distribution goes above and below the simulated SCD and TCD curves when compared from LCD and HCD end of the electrode. Overall, in all the cases, experimental dimensionless deposit thickness distribution followed the simulated SCD and TCD curves in a reasonable way.

Symbols

c:: Concentration at the surface of the working electrode (mol cm⁻³)
D:: Diffusion coefficient of electroactive species (Cu²⁺) (cm² s⁻¹)
F:: Faraday constant (C mol⁻¹)
h:: Distance between the electrodes at HCD end (see Figure 2(a))
i_avg:: Applied average current density (A cm⁻²)
i_j:: Partial current density obtained from the electrode reaction, j (A cm⁻²)
i_l:: Local current density at any point in the modified Hull cell (A cm⁻²)
i(x)/i_avg:: Normalized current distribution
i_0,j:: Exchange current density at bulk concentrations for reaction, j (A cm⁻²)
j:: Electrode reaction and imaginary number,
K₁, K₂, c, h^′:: Quantities used in the conformal mappings (see (1) and (2) and Figure 2)
L:: Length of the cathode (cm)
M:: Molar mass of Cu (g mol⁻¹)
N:: Flux of electroactive species (Cu²⁺) (mol cm⁻² s⁻¹)
n_j:: Number of electrons transferred in an electrode reaction, j (A cm⁻²)
R:: Universal gas constant (8.3143 J mol⁻¹K⁻¹)
RkΔ:: Dimensionless cell resistance (see Figure 2(a) and (18))
t:: Total deposition time (s)
T:: Absolute temperature (K)
V_Eq,j:: Equilibrium potential for the reaction, j (V)
W_a:: Wagner number for a Tafel kinetic approximation
x, y:: (Dimensionless) real and imaginary components of z-complex coordinate system
z, w, χ:: Complex coordinate systems used in the conformal mappings (see Figure 2).

Abbreviations

HCD:: High current density
LCD:: Low current density
PCD:: Primary current distribution
PED:: Pulsed electrodeposition
SCD:: Secondary current distribution
TCD:: Tertiary current distribution.

Greek Symbols

α_c,j:: Cathodic transfer coefficient of reaction, j
β_c:: Cathodic Tafel slope (V)
η_j:: Overpotential for the reaction, j (V)
θ:: Angle formed at a corner of the working electrode and insulating wall (radians) (see Figure 2(a))
κ:: Conductivity of the electrolyte (S cm⁻¹)
μ:: Experimental thickness of the electrodeposited Cu thin film (μm)
μ_avg:: Theoretical thickness of the electrodeposited Cu thin film (μm)
ξ:: Normal to the cathode surface (cm)
π:: 3.1415926…
ρ:: Density of Cu (8.93 g cm⁻³)
ϕ:: Potential (V)
ϕ_l:: Electrolyte potential (V)
ϕ_s,0:: Electrode potential (V).

Superscript

b:: Bulk
s:: Surface.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

The authors are indebted to Dr. Challa Subrahmanya Sastry (Department of Mathematics, IITH) and Dr. Jampana Phanindra (Department of Chemical Engineering, IITH) for the technical discussions to calculate primary current distribution analytically using conformal mapping technique. The authors also would like to thank BVRSN Prasad, K. Manjunath, and M. Srinivas for their help in developing the MATLAB program. This research work has been financially supported by Council of Scientific and Industrial Research (CSIR) (CSIR Sanction no. 22(0585)/12/EMR-II), India.

References

1 Devaraj G. and Seshadri S. K., Pulsed electrodeposition of copper, Plating & Surface Finishing. (1992) 79, no. 8, 72–78.
CAS Google Scholar
2 Srinivas P., Hamann S., Wambach M., Ludwig A., and Dey S. R., Fabrication of a Ni-Cu thin film material library using pulsed electrodeposition, Journal of The Electrochemical Society. (2014) 161, no. 10, D504–D509, https://doi.org/10.1149/2.0451410jes.
10.1149/2.0451410jes
CAS Web of Science® Google Scholar
3 Matlosz M., Creton C., Clerc C., and Landolt D., Secondary current distribution in a hull cell: boundary element and finite element simulation and experimental verification, Journal of the Electrochemical Society. (1987) 134, no. 12, 3015–3021, https://doi.org/10.1149/1.2100332, 2-s2.0-0023579388.
10.1149/1.2100332
CAS Web of Science® Google Scholar
4 Orazem M. E. and Newman J., Primary current distribution and resistance of a slotted-electrode cell, Journal of the Electrochemical Society. (1984) 131, no. 12, 2857–2861, https://doi.org/10.1149/1.2115431, 2-s2.0-0021582325.
10.1149/1.2115431
CAS Web of Science® Google Scholar
5 Kadper C., The theory of the potential and the technical practice of electrodeposition: I. The general problem and the cases of uniform flow, Journal of the Electrochemical Society. (1940) 77, no. 1, 353–363, https://doi.org/10.1149/1.3521208.
10.1149/1.3521208
Google Scholar
6 Kasper C., The theory of the potential and the technical practice of electrodeposition V. The two-dimensional rectangular enclosures, Transactions of the Electrochemical Society. (1942) 82, no. 1, 153–185, https://doi.org/10.1149/1.3071405.
10.1149/1.3071405
Google Scholar
7 Newman J., Resistance for flow of current to a disk, Journal of the Electrochemical Society. (1966) 113, no. 5, 501–502, https://doi.org/10.1149/1.2424003.
10.1149/1.2424003
CAS Web of Science® Google Scholar
8 MiksisJ. J.Jr. and Newman J., Primary resistances for ring-disk electrodes, Journal of the Electrochemical Society. (1976) 123, no. 7, 1030–1036, 2-s2.0-0016974492.
10.1149/1.2132986
CAS Web of Science® Google Scholar
9 Pierini P. and Newman J., Potential distribution for disk electrodes in axisymmetric cylindrical cells, Journal of the Electrochemical Society. (1979) 126, no. 8, 1348–1352, https://doi.org/10.1149/1.2129275, 2-s2.0-0018504478.
10.1149/1.2129275
CAS Web of Science® Google Scholar
10 Moulton H. F., Current flow in rectangular conductors, Proceedings of the London Mathematical Society. (1905) 2-3, no. 1, 104–110, https://doi.org/10.1112/plms/s2-3.1.104, MR1575922.
10.1112/plms/s2-3.1.104
Google Scholar
11 Kadaner L. I. and Tsukernik V. M., The current distribution in the plane parallel electrodes in a rectangular electrolyzer, Russian Journal of Physical Chemistry. (1957) 31, no. 10, 2253–2269.
CAS Google Scholar
12 Wagner C., Theoretical analysis of the current density distribution in electrolytic cells, Journal of the Electrochemical Society. (1951) 98, no. 3, 116–128, https://doi.org/10.1149/1.2778113.
10.1149/1.2778113
CAS Web of Science® Google Scholar
13 Wagner C., Calculation of the current distribution at electrodes involving slots, Plating. (1961) 48, 997–1002.
CAS Google Scholar
14 Kronsbein J., The effect of insulating and conducting shields and partly stopped-off electrodes on current distribution in electrolytic cells, Proceedings of the London Mathematical Society. Second Series. (1947) 49, no. 1, 260–281, MR0020938.
Web of Science® Google Scholar
15 Kronsbein J., Current and metal distribution in electrodeposition. I. Critical review of the literature, Plating. (1950) 37, 851–854.
CAS Google Scholar
16 Breiter M. and Guggenberger T., Über die elimination der widerstandsüberspannung an drahtförmigen elektroden mittels der methode der abstandsvariation, Zeitschrift für Elektrochemie. (1956) 60, no. 6, 594–603, https://doi.org/10.1002/bbpc.19560600611.
10.1002/bbpc.19560600611
CAS Google Scholar
17 Hine F., Yoshizawa S., and Okada S., Effect of the walls of electrolytic cells on current distribution, Journal of the Electrochemical Society. (1956) 103, no. 3, 186–193, https://doi.org/10.1149/1.2430263.
10.1149/1.2430263
CAS Web of Science® Google Scholar
18 Diem C. B., Newman B., and Orazem M. E., The influence of small machining errors on the primary current distribution at a recessed electrode, Journal of the Electrochemical Society. (1988) 135, no. 10, 2524–2530, https://doi.org/10.1149/1.2095369, 2-s2.0-0024092606.
10.1149/1.2095369
CAS Web of Science® Google Scholar
19 West A. C., Matlosz M., and Landolt D., Primary current distribution in the Hull cell and related trapezoidal geometries, Journal of Applied Electrochemistry. (1992) 22, no. 3, 301–303, https://doi.org/10.1007/bf01030192, 2-s2.0-0026835545.
10.1007/BF01030192
CAS Web of Science® Google Scholar
20 Fleck R. N., Numerical evaluation of current distribution in electrical systems [M.S. thesis], 1964, University of California, Berkeley, Calif, USA.
Google Scholar
21 Churchill R. V., Complex Variables and Applications, 1960, 2nd edition, McGraw-Hill, New York, NY, USA, MR0112948.
Google Scholar
22 Copson E. T., An Introduction to the Theory of Functions of a Complex Variable, 1935, Oxford University Press, London, UK.
Google Scholar
23 Bowman F., Introduction to Elliptic Functions with Applications, 1953, John Wiley and Sons, New York, NY, USA.
Google Scholar
24 Rubenfeld L. A., A First Course in Applied Complex Variables, 1985, McGraw-Hill, New York, NY, USA.
Google Scholar
25 Norm 50950 DIN (Deutsches Institut fur Normung), Mikroskopische Messung der Schichtdicke, TAB 175, 1983, Beuth Verlag GmbH, Berlin, Germany.
Google Scholar
26 Lima F., Mescheder U., and Reinecke H., Simulation of current density for electroplating on silicon using a Hull cell, Proceedings of the COMSOL Conference, March 2012, Milan, Italy.
Google Scholar
27 Tong L., Tertiary current distributions on rotating electrodes, Proceedings of the COMSOL Conference, 2011, Tokyo, Japan.
Google Scholar
28 Low C. T. J., Roberts E. P. L., and Walsh F. C., Numerical simulation of the current, potential and concentration distributions along the cathode of a rotating cylinder Hull cell, Electrochimica Acta. (2007) 52, no. 11, 3831–3840, https://doi.org/10.1016/j.electacta.2006.10.056, 2-s2.0-33847064747.
10.1016/j.electacta.2006.10.056
CAS Web of Science® Google Scholar
29 Zhang Z., Zhang J. Q., Leng W. H., and Cao C. N., Investigation of the secondary current distribution in a hull cell, Journal of the Electrochemical Society. (2001) 148, no. 7, C488–C491, https://doi.org/10.1149/1.1377594, 2-s2.0-0442329148.
10.1149/1.1377594
CAS Web of Science® Google Scholar
30 Jagush F. A., White R. E., and Ryan W. E., Predicted secondary current distributions for linear kinetics in a modified three-dimensional Hull cell, Journal of the Electrochemical Society. (1990) 137, no. 6, 1848–1851, https://doi.org/10.1149/1.2086815, 2-s2.0-0025448880.
10.1149/1.2086815
CAS Web of Science® Google Scholar
31 Beattie S. D. and Dahn J. R., Comparison of electrodeposited copper-zinc alloys prepared individually and combinatorially, Journal of the Electrochemical Society. (2003) 150, no. 11, C802–C806, https://doi.org/10.1149/1.1615998, 2-s2.0-0242425798.
10.1149/1.1615998
CAS Web of Science® Google Scholar
32 Beattie S. D. and Dahn J. R., Single-bath electrodeposition of a combinatorial library of binary Cu_1−xSn_x alloys, Journal of the Electrochemical Society. (2003) 150, no. 7, C457–C460, https://doi.org/10.1149/1.1576769, 2-s2.0-0038106360.
10.1149/1.1576769
CAS Web of Science® Google Scholar
33 Beattie S. D. and Dahn J. R., Combinatorial electrodeposition of ternary Cu–Sn–Zn alloys, Journal of the Electrochemical Society. (2005) 152, no. 8, C542–C548, https://doi.org/10.1149/1.1939211, 2-s2.0-25644434817.
10.1149/1.1939211
CAS Web of Science® Google Scholar
34 Madore C., Matlosz M., and Landolt D., Experimental investigation of the primary and secondary current distribution in a rotating cylinder Hull cell, Journal of Applied Electrochemistry. (1992) 22, no. 12, 1155–1160, https://doi.org/10.1007/BF01297417, 2-s2.0-0026981968.
10.1007/BF01297417
CAS Web of Science® Google Scholar
35 Chassaing E., Vu Quang K., and Wiart R., Kinetics of copper electrodeposition in citrate electrolytes, Journal of Applied Electrochemistry. (1986) 16, no. 4, 591–604, https://doi.org/10.1007/BF01006854, 2-s2.0-0022757338.
10.1007/BF01006854
CAS Web of Science® Google Scholar
36 Carneval G. and de Cusminsky J. B., The influence of the anion on copper electrocrystallization, Journal of the Electrochemical Society. (1981) 128, no. 6, 1215–1221, https://doi.org/10.1149/1.2127596, 2-s2.0-0019579308.
10.1149/1.2127596
CAS Web of Science® Google Scholar
37 Podlaha E. J., Bonhote Ch., and Landolt D., Mathematical model and experimental study of the electrodeposition of Ni-Cu alloys from complexing electrolytes, Electrochimica Acta. (1994) 39, no. 18, 2649–2657, https://doi.org/10.1016/0013-4686(94)00308-4, 2-s2.0-0028755391.
10.1016/0013-4686(94)00308-4
CAS Web of Science® Google Scholar
38 Lange N. A., Lange′s Handbook of Chemistry, 1979, 12th edition, Wiley, New York, NY, USA.
Google Scholar
39 Ying R. Y., Ng P. K., Mao Z., and White R. E., Electrodeposition of copper-nickel alloys from citrate solutions on a rotating disk electrode, Journal of the Electrochemical Society. (1988) 135, no. 12, 2964–2971, https://doi.org/10.1149/1.2095470, 2-s2.0-0024144203.
10.1149/1.2095470
CAS Web of Science® Google Scholar
40 Rode S., Henninot C., Vallières C., and Matlosz M., Complexation chemistry in copper plating from citrate baths, Journal of the Electrochemical Society. (2004) 151, no. 6, C405–C411, https://doi.org/10.1149/1.1715092, 2-s2.0-2942666220.
10.1149/1.1715092
CAS Web of Science® Google Scholar
41 Ibl N., Distribution du courant dans les systèmes électrochimiques, Techniques de L′ingénieur D. (1976) 902, 1–78.
Google Scholar
42 Kardos O., Current distribution on microprofiles. Part I, Plating. (1974) 61, no. 2, 129–138.
Google Scholar
43 Kardos O., Current distribution on microprofiles. Part II, Plating. (1974) 61, no. 3, 229–237.
Google Scholar
44 Kardos O., Current distribution on microprofiles. Part III, Plating. (1974) 61, no. 4, 316–325.
Google Scholar
45 Bozzini B., Lacitignola D., Mele C., and Sgura I., Morphogenesis in metal electrodeposition, Note di Matematica. (2012) 32, no. 1, 7–46, https://doi.org/10.1285/i15900932v32n1p7, MR2986386, ZBL1264.78027, 2-s2.0-84869494442.
10.1285/i15900932v32n1p7
Google Scholar
46 Ibañez A. and Fatás E., Mechanical and structural properties of electrodeposited copper and their relation with the electrodeposition parameters, Surface & Coatings Technology. (2005) 191, no. 1, 7–16, https://doi.org/10.1016/j.surfcoat.2004.05.001, 2-s2.0-10344261552.
10.1016/j.surfcoat.2004.05.001
CAS Web of Science® Google Scholar

Citing Literature

All articles

Theoretical and Experimental Study of Copper Electrodeposition in a Modified Hull Cell

Abstract

1. Introduction

2. Computational and Experimental Methods

2.1. Analytical Solution of PCD in the Modified Hull Cell

2.1.1. Description of Modified Hull Cell

2.1.2. Calculation of PCD in the Modified Hull Cell

2.2. Numerical Simulation of Cu Electrodeposition

2.2.1. Geometry of the Modified Hull Cell

2.2.2. Theoretical Development

2.3. Experimental

2.3.1. Cu Electrodeposition

2.3.2. Scanning Electron Microscopy (SEM)

2.3.3. Thickness Measurements with Optical Profiler

2.3.4. Transport and Kinetic Parameters

3. Results and Discussion

3.1. Analytical Solution of PCD for Modified Hull Cell

3.2. Primary Resistance of the Modified Hull Cell

3.3. Numerical Solution of Current Density Distributions (Primary, Secondary, and Tertiary) for Modified Hull Cell

3.3.1. Current Density Distribution Lines

3.3.2. Primary Current Distribution

3.3.3. Comparison between Analytical and Numerical Simulation Solutions of PCD

3.3.4. Secondary Current Density Distribution

3.3.5. Tertiary Current Density Distribution

3.3.6. Comparison of Simulation and Experimental Values

4. Surface Appearance and Morphological Analyses of Cu Films

5. Summary

Symbols

Abbreviations

Greek Symbols

Superscript

Conflict of Interests

Acknowledgments

References

Citing Literature

Figures

References

Related

Information