A new class of 3D autonomous quadratic systems, the dynamics of which demonstrate a chaotic behavior, is found. This class is a generalization of the well-known class of Lorenz-like systems. The existence conditions of limit cycles in systems of the mentioned class are found. In addition, it is shown that, with the change of the appropriate parameters of systems of the indicated class, chaotic attractors different from the Lorenz attractor can be generated (these attractors are the result of the cascade of limit cycles bifurcations). Examples are given.

1. Introduction

Chaos is a very interesting nonlinear phenomenon, which has been intensively studied in the last four decades. Many potential applications have come true in secure communication, laser and biological systems, hydrodynamics and chemical technologies, and other areas (see, e.g., [1, 2] and many references cited therein).

Notice that interest in the study of the chaotic systems increases only (see, e.g., [3–19]). We will specify a few scientific directions, in which application of methods of chaotic dynamics appeared most effective.

In the scientific literature, chaotic economic systems have got much attention because their complex dynamic behaviors cannot be described by traditional models. Recently, a few researches on the usage of these systems in cryptographic algorithms have been conducted. A new image encryption algorithm based on a chaotic economic map is proposed. Implementation of the proposed algorithm on a plain image based on the chaotic map is performed [3].

The paper [4] investigates the multipulse heteroclinic bifurcations and chaotic dynamics of a laminated composite piezoelectric rectangular plate by using an extended Melnikov method in the resonant case.

A chaotic system arising from double-diffusive convection in a fluid layer is investigated in [5] based on the theory of dynamical systems. A five-dimensional model of chaotic systems is obtained using the Galerkin truncated approximation. The results showed that the transition from steady convection to chaos via the Hopf bifurcation produced a limit cycle, which may be associated with a homoclinic explosion at a slightly subcritical value of the Rayleigh number.

The paper [6] investigates the problem of two kinds of function projective synchronization of financial chaotic system with definite integration scaling function, which are not fully considered in the existing researches. In this paper, the following two questions (unlike previous methods) are investigated: (1) two kinds of the definite integration scaling function projective synchronization are given and (2) the upper and lower limit of the definite integral scaling function are the bound dynamical systems.

In this connection, the important problem is the establishment of theoretical results, where it is possible to extend the wide classes of the dynamical systems. One of such classes is the class of 3D quadratic systems.

Vast scientific literature is devoted to researches of different types of systems of this class. For instance, 3-scroll and 4-scroll chaotic attractors were investigated in [7]. New existence conditions of heteroclinic and homoclinic orbits were found in [8–10]. New three-wing and four-wing chaotic attractors were opened in [11–14]. The article [15] summarizes investigations of quadratic dynamical systems, which are indicated in [7–14].

Another interesting domain of nonlinear dynamics is the control by the chaotic systems. Novel controllers for stabilization and tracking of chaotic and hyperchaotic Lorenz systems using extended backstepping techniques were proposed in [16]. Based on the proposed approach, the generalized weighted controllers were designed to control the chaotic behavior as well as achieve synchronization in chaotic and hyperchaotic Lorenz systems [16].

Above, we mentioned researches of the class of 3D quadratic dynamical systems. The well-known Lorenz system, which is described by the equations

()

is a basic representative of this class (here, σ = 10, b = 8/3, and r > 24).

System (1) is a three-dimensional autonomous system with only two quadratic terms in its nonlinearity, which is very simple in the algebraic structure and yet is fairly complex in dynamical behaviors. The observation of these two seemingly contradictory aspects of the Lorenz system thereby triggered a great deal of interest from the scientific community to seek closely related Lorenz-like systems, by different motivations and from various perspectives [15].

It should be said (as it was noted in [15]) that almost all known chaotic attractors of 3D quadratic dynamical systems can be generated (at the appropriate values of parameters) by the following system:

()

where a₁₁, …, a₃₃, m₁, …, m₆, and c are real parameters.

The primary purpose, which was pursued by the research program that was begun in this work, is to set communication between algebraic and geometric properties of solutions of system (2).

In spite of the vast researches, which are developed in connection with the dynamics of the Lorenz system, a lot of the unsolved problems yet remain. A strange attractor corresponds to the complex nonperiodic mode of the Lorentz system. The system also generates spatial limit cycles in three-dimensional space. A few papers are devoted to the research of the complex closed trajectories which are also connected to chaos, because a transition to the chaotic behavior is sometimes realized in consequence of bifurcations of periodic trajectories on saddle trajectories. Recently (see [17–19]), a row of results describing the behavior of the Lorenz-like systems appeared. The present article is one of such results.

In conclusion, we explain the name of the article. At first sight, it seems that such systems are simpler than 3D systems in which all three equations are nonlinear. However, the existence of one linear equation in system (2) makes application of the theory of positive (or negative) definite quadratic forms impossible. This definiteness was widely used in [17, 18].

In the present paper, some special cases of system (2) will be considered. Note that in system (1) two nonlinearities exist: there are x · y and x · z. In the system which will be studied below, we also will have two nonlinearities: x · (d_yy + d_zz) and y · (d_yy + d_zz), where d_y and d_z are real numbers such that . In our opinion, this is some generalization of system (1). In addition, in this work, the researches begun in [17, 18] will be continued.

2. Bounded Solutions of Quadratic Dynamical Systems

Consider the following 3D autonomous quadratic system:

()

where x = (x, y, z) ^T; H = {h_ij}, i, j = 1, …, 3, is a real (3 × 3)-matrix; and

()

are real quadratic polynomials.

Suppose that the matrix

()

has rank 1 or 2. Then, by suitable linear transformations of variables x → x₁ + α₁y₁ + α₂z₁ (

), y → y₁, and z → z₁, system (3) can be represented in the same form as (3), where

, i, j = 1, …, 3, and

()

and

. (Note that if the rank of matrix (5) is equal to 1, then the case

is not excepted.)

Thus, it can be considered that, for system (3), the conditions

()

are fulfilled.

Introduce into system (3) (taking into account (7)) new variables ρ and ϕ under the formulas y = ρcos⁡ϕ and z = ρ sin ϕ, where ρ > 0. Then, after replacement of variables and multiplication of the second and third equations of system (3) on the matrix

()

we get

()

Consider the first and second equations of system (9):

()

where ϕ is a real parameter; and

()

In [17, 18], conditions of appearance of chaos in system (3) were analyzed. As a result of this analysis, the following theorem (with small corrections by comparison to [16, 17]) was proved.

Let Δ₁(cos⁡ϕ, sin ϕ) ≡ h₁₁ · h(cos⁡ϕ, sin ϕ) − f(cos⁡ϕ, sin ϕ) · g(cos⁡ϕ, sin ϕ), Δ₂(cos⁡ϕ, sin ϕ) ≡ f₂₂(cos⁡ϕ, sin ϕ) · g₁₂(cos⁡ϕ, sin ϕ), and be the bounded functions.

Theorem 1 (see [17], [18].)Let h₁₁ < 0. Suppose also that for system (10) the following conditions are fulfilled:

(i)
Δ₂(u, v) is a nonsingular form of the variables u ≡ cos⁡ϕ and v ≡ sin ϕ.
(ii)
Either Δ₁(cos⁡ϕ, sin ϕ) is a negative constant or Δ₁(cos⁡ϕ, sin ϕ) is a periodic nonpositive function or Δ₁(cos⁡ϕ, sin ϕ) is a periodic alternating in sign on (−∞, ∞) function.
(iii)
Δ₂(cos⁡ϕ, sin ϕ) and Δ₃(cos⁡ϕ, sin ϕ) are periodic nonpositive functions.

Suppose that the condition

()

is also valid. (From this condition, it follows that ∀ϵ > 0 there exists a numerical sequence t_n → ∞ as n → ∞ such that, ∀n ρ(t_n) < ϵ.)

Then, in system (9) (and system (3)), there are chaotic dynamics.

3. Definition of Essentially Singular 3D Dynamical Systems

The general definition of the singular system was given in [19]. In the present paper, we are restricted by a narrower definition.

Consider the following 2D autonomous quadratic system:

()

where a₁₁, …, a₂₂, b₁₁, …, b₂₂, and c₁₁, …, c₂₂ are real numbers.

Introduce the following real (2 × 2)-matrices:

()

Replace variables x, y in system (13) by new variables x₁, y₁ under the formula

()

where S is a linear transformation from the group

of all linear inverse transformations of the space

[19]. In this case, the triple of matrices (A, T₁, T₂) transforms into triple S∘(A, T₁, T₂) = (S⁻¹AS, (S⁻¹T₁, S⁻¹T₂)·(S ⊗ S)).

Remember that a scalar polynomial f(A, T₁, T₂) is called an invariant of weight l of the group , if and ∀(A, T₁, T₂); we have f(S∘(A, T₁, T₂)) = (det S) ^l × f(A, T₁, T₂), where l ≥ 0 is some integer.

With the help of matrices T₁, T₂, we construct the auxiliary not depending on A invariants of weight 2 [19]:

()

where tr P is a trace of the square matrix P.

Now, we can introduce the main invariant of the present paper

()

of weight 2 [19].

In system (13), we replace the variable y by the variable ρ. Now, we can replace the coefficients of system (13) by appropriate coefficients of system (10). (In this case, the invariants J₂ and D will be the functions of the variable ϕ: D(cos⁡ϕ, sin ϕ), J₂(cos⁡ϕ, sin ϕ).)

Let u ≡ cos⁡ϕ and v ≡ sin ϕ.

Definition 2 (see [19].)System (3) is called essentially singular if for arbitrary real number ϕ the conditions D(u, v) ≡ D(cos ϕ, sin ϕ) ≤ 0 and J₂(u, v) ≡ J₂(cos ϕ, sin ϕ) ≤ 0 are fulfilled. In addition, there exist the numbers ϕ_i such that D(cos ϕ_i, sin ϕ_i) = J₂(cos ϕ_i, sin ϕ_i) = 0, i = 1,2, ….

We compute the invariants J₂(u, v) and D(u, v) for system (3) under conditions c₁₂ = c₁₃ = c₂₂ = c₂₃ = c₃₃ = 0. Then, we have

()

From here, it follows that if D(u, v) ≤ 0 (D(u, v) < 0), then J₂(u, v) ≤ 0 (J₂(u, v) < 0).

4. Lorenz-Like Systems

Consider the following system:

()

Here, we will consider that h₁₁ < 0, k > 0, h₃₂ ≠ 0, and the equilibrium (0,0, 0) ^T is a saddle point. In addition, in this section, we will consider that h₂₁ = h₃₁ = 0.

The direct calculations of the invariants D(cos⁡ϕ, sin ϕ) and J₂(cos⁡ϕ, sin ϕ) of system (19) show that J₂(cos⁡ϕ, sin ϕ) = −k³ · (cos⁡ϕ) ⁴ · (a₂₂cos⁡ϕ + a₂₃ sin ϕ) ⁴ and D(cos⁡ϕ, sin ϕ) = 4J₂(cos⁡ϕ, sin ϕ). Thus, we have D(cos⁡ϕ_i, sin ϕ_i) = J₂(cos⁡ϕ_i, sin ϕ_i) = 0 at ϕ_i = π/2 + 2π · i or ϕ_i = −arctan(a₂₂/a₂₃) + π · i, i = 0,1, 2, …, and it is clear that system (19) is essentially singular.

System (19) is a special case of system (3). (If we put h₁₁ = −b = −8/3, h₂₂ = −1, h₂₃ = r > 0, h₃₂ = −σ = −10, h₃₃ = σ = 10, h₁₂ = h₁₃ = 0, a₂₂ = 0, a₂₃ = 1, and k = 1, then system (19) becomes the classic chaotic Lorenz system.) In coordinates y = ρcos⁡ϕ and z = ρ sin ϕ, system (19) takes the following form (see (9)):

()

For this system, we have Δ₂(cos⁡ϕ, sin ϕ) = −k(cos⁡ϕ · (a₂₂cos⁡ϕ + a₂₃ sin ϕ)) ² ≤ 0, Δ₃(cos⁡ϕ, sin ϕ) = 4Δ₂(cos⁡ϕ, sin ϕ) = −4k(cos⁡ϕ · (a₂₂cos⁡ϕ + a₂₃ sin ϕ)) ² ≤ 0. Thus, conditions (i)–(iii) of Theorem 1 are fulfilled.

From the last equation of system (20), we have

()

Theorem 3. Let the equilibrium point (0,0, 0) of system (19) be saddle. Suppose also that for this system the following conditions are valid:

(i)
h₁₁ < 0, h₂₁ = h₃₁ = 0.
(ii)
.
(iii)
There exists a finite limit
()
(iv)
.

Then, all solutions of system (19) are bounded.

Proof. Construct the two following quadratic forms:

()

Introduce the designations

()

(Here, the symmetric matrices F and G are matrices of the forms f(u, v) and g(u, v).)

Compute the eigenvalues of the matrices F and G. By λ_min(F) and λ_max(H) (λ_min(G) and λ_max(G)), denote minimal and maximal eigenvalues of the matrix F (the matrix G). Then, we have

()

Since the point (0,0, 0) is saddle, then det H ≠ 0. Besides, in order for condition (22) to be satisfied, it is necessary that the form g(u, v) was negative definite. In this case, we can consider the following two possibilities:

()

For research of system (20), we use the known in theory of differential equations Comparison Principle (see [17, 18]). Then, with the help of inequalities (26) and (27), we get instead of system (20) the following system:

()

By virtue of condition (22) at t → ∞, system (28) can be transformed to the following system with periodic coefficients:

()

Now, we will consider that for some values of parameters system (29) has a periodic solution. (This means that systems (19) and (20) have also the periodic solutions.)

Suppose that the number t_m ≥ 0 satisfies the conditions pt_m = pt₀ + mπ and the number cos (pt_m)(a₂₂cos (pt_m) + a₂₃ sin (pt_m)) ≠ 0, where m = 0,1, 2, ….

Further, we will consider the solutions of system (29) in a small neighborhood of the point t_m: , m = 0,1, 2, …. With initial conditions x_m0, ρ_m0 for system (29), the solutions of system (28) in the point t_m are appointed.

Suppose that the time t₀ also satisfies the condition

()

From here, it follows that

()

If we will take into consideration formula (32), the second equation of system (29) can be rewritten as

()

Let

()

Then, from (33), we have the equation

()

The solution of this equation is

()

In our case, we can introduce the function

()

where

()

We take advantage of the known Cauchy inequality: ; here, 〈w₁, w₂〉 is a scalar product of the vectors w₁ and w₂. Then, it is possible to get the following estimation of the function c(t):

()

Thus, from here, we get the fourth condition of Theorem 3.

Further, formula (36) can be rewritten as

()

Above, it was shown that if ∀t ≥ 0 we have b(t) ≥ 0, then . Therefore, we can consider that there exist the positive constants c_min and c_max such that 0 < c_min ≤ c(t) ≤ c_max. Thus, from here and the condition t → ∞, it follows that

()

and, therefore, the solution ρ(t) of system (29) is bounded. Since h₁₁ < 0, then from the first equation of system (29) it follows that the solution x(t) is also bounded. In turn, this means the boundedness of solutions of systems (19) and (20). The proof is finished.

Note that if a₂₂ = 0 and k = 1, then system (19) is the classic Lorentz-like system and condition (iv) becomes trivial.

Theorem 4. Let the equilibrium point (0,0, 0) of system (19) be a saddle-focus. Then, under the conditions of Theorem 3 in system (19), there exists a limit cycle.

Proof. Let us calculate Lyapunov’s exponent Λ for a real function f(t) [17, 18]:

()

We take advantage of the following properties Lyapunov’s exponents:

(i)
Λ[f₁(t) · f₂(t)] ≤ Λ[f₁(t)] + Λ[f₂(t)].
(ii)
If Λ[f(t)] < 0, then
(iii)
Λ[f₁(t) + f₂(t)] ≤ max(Λ[f₁(t)], Λ[f₂(t)]).
(iv)
Λ[d · f(t)] = Λ[f(t)] (d ≠ 0).

Taking into account the boundedness of solutions x(t) and ρ(t) of system (28), we have Λ[x] ≤ 0, Λ[ρ] ≤ 0.

We write the first equation of system (28) in the integral form

()

From here and (i), it follows that Λ(exp(h₁₁t)ξ(t)) ≤ Λ(exp(h₁₁t)) + Λ(ξ(t)) ≤ h₁₁ + 0 = h₁₁ or Λ(exp(h₁₁t)ξ(t)) = −∞. Thus, from (ii) and (iii), it follows that

()

Therefore, from boundedness of x(t) and conditions (i), (iii), and (iv), we have Λ[x(t)] ≤ h₁₁ < 0.

Further, the function ρ(t) is bounded. Consequently, we get that Λ[ρ(t)] ≤ 0. In addition, from conditions (22), it follows that ϕ(t) → pt. Thus, we have Λ[ϕ(t)] = 0. Since for the limit cycle another Lyapunov exponent is equal to zero, then from here it follows that if Λ[ρ(t)] < 0, then this cycle is stable; if Λ[ρ(t)] = 0, then we have a limit torus.

Let again the point (0,0, 0) be a saddle-focus. We note that if in system (19) we do the replacement of variables y → αy₁ + βz₁, z → γy₁ + δz₁ (αδ − βγ ≠ 0) such that

()

then the form g(u, v) becomes positive definite. In this case, formula (21) can be represented in the form ϕ(t) = ϕ₀ + pt + ⋯ and condition (22) is always fulfilled. From here, it follows that, in system (28), which was used in the Comparison Principle, there exists a limit cycle.

Let

()

be an ellipsoid with the center in the point (−s, 0,0), where

()

Theorem 5. Assume that h₂₁ = h₃₁ = 0 and a₂₃ ≠ 0. Suppose also that h₁₁ < 0, ska₂₂ + h₂₂ < 0, and h₃₃ < 0. If the start point , then ∀t > 0 the trajectory (x(t, x₀), y(t, y₀), z(t, z₀)) of system (19) is completely contained in . Thus, the ellipsoid is a basin of system (19).

Proof. Let V(t) = (x(t) + s) ² + y²(t)/k + z²(t) ≥ 0 be a positive definite function. Then, from system (19), we have

()

In order for the condition to be fulfilled ∀t ≥ 0, it is necessary that

()

Let

()

be an open ellipsoid with the center in the point (−s/2,0, 0).

Let also

()

be the open ellipsoid with the center in the point (−s/2,0, 0) and semiaxes

()

(The ellipsoid

is an interior part of domain (49); thus, domain (49) is the set

It is clear that . This means that trajectories incoming in the ellipsoid at all t ≥ 0 remain in this ellipsoid. Consequently, these trajectories are bounded. The proof is finished.

Notice that Theorem 5 is weaker than Theorems 1, 3, and 4. However, verification of its conditions is constructive.

5. Examples

We will consider that for system (19) the conditions of either Theorem 3 or Theorem 4 are satisfied.

At first, we compute equilibrium points of system (19). We have the equilibrium point (0,0, 0) and two equilibrium points (x_e, y_e, z_e), where

()

Thus, if h₃₃ det H < 0, then there are three equilibrium points (including the point (0,0, 0)); if h₃₃ det H > 0, then there is only one equilibrium point (0,0, 0). It is easy to check that all equilibrium points will be either saddle-nodes or saddle-focuses or such points, Jacobi’s matrix of which has three positive eigenvalues.

Further, we will study not only situations described in Theorems 3 and 4, but also the cases h₂₁ ≠ 0 and h₃₁ ≠ 0. It is necessary with the changes of the parameters h₂₁ and h₃₁ to realize the cascade of the limit cycle bifurcations at transition from this cycle to the chaotic attractor.

A special case arises, when the condition a₂₂h₃₃ − a₂₃h₃₂ = 0 takes place. In this case, there exists only one unstable equilibrium point (0,0, 0).

Consistently, consider all indicated situations:

The case a₂₂h₃₃ − a₂₃h₃₂ ≠ 0.
The case a₂₂h₃₃ − a₂₃h₃₂ = 0. In this case, if the discriminant (h₂₂ + h₃₃) ² − 4 det H < 0, then system (19) demonstrates the existence of limit cycles. If (h₂₂ + h₃₃) ² − 4 det H > 0, then in system (19) no stable attractor was found.

6. Conclusion

In the present paper, an attempt to investigate the chaotic dynamics of system (19) was made. This system is a generalization of the known Lorenz system (1). Theorems 3 and 4, by which it is possible not only to build bounded solutions of system (19), but also to predict the existence of spatial limit cycles in this system, were also proved (see Figures 1(a), 2(a)–2(c), and 3(a)–3(c)). As a result, two new chaotic attractors (see Figures 3(d) and 4(f)) were found. Their chaotic behavior is confirmed by Theorem 1 (see Figure 4(d)). (At the same time, Figures 4(c) and 4(e) demonstrate the presence of the limit cycle in system (19) for the specific values of parameters; besides, Figures 4(a) and 4(b) confirm that condition (iv) of Theorem 3 is fulfilled.)

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

The phase portrait of a quasi-periodic behavior (a) and the graph of the function ρ(t) (b) of system (19) at h₁₁ = −0.1, h₂₂ = h₃₃ = 4, h₂₃ = −h₃₂ = 40, k = 1, a₂₂ = −1, and a₂₃ = 1.

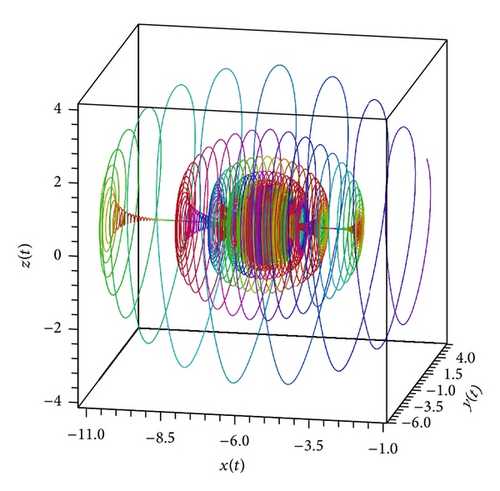
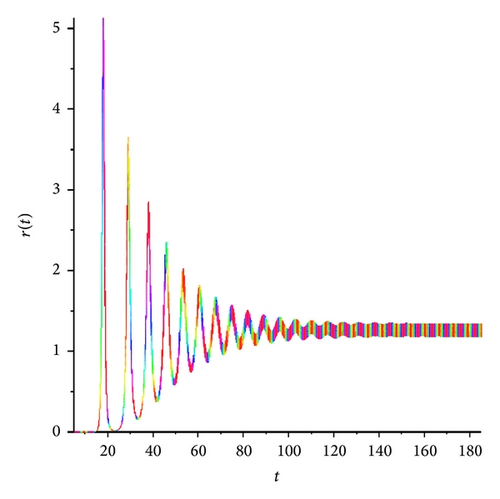
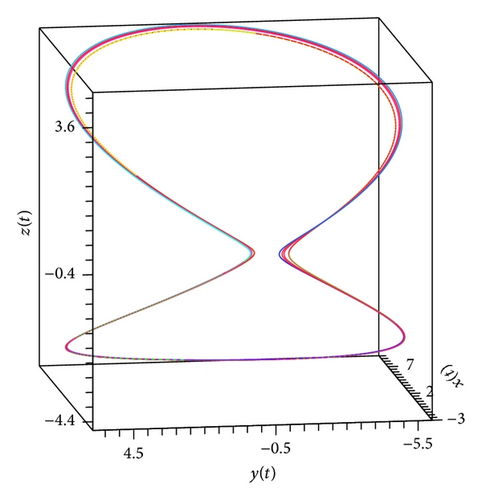
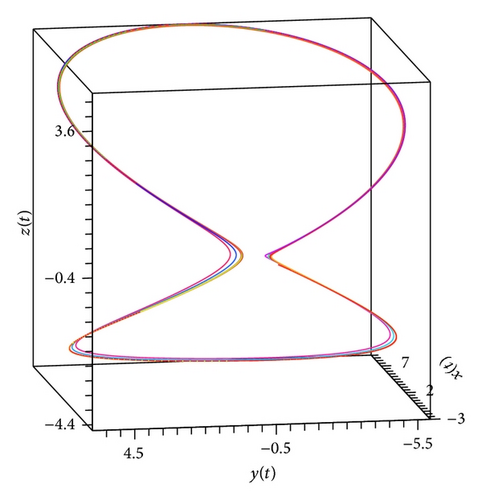
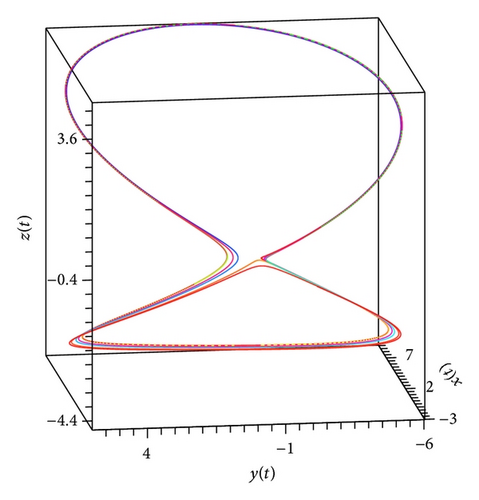
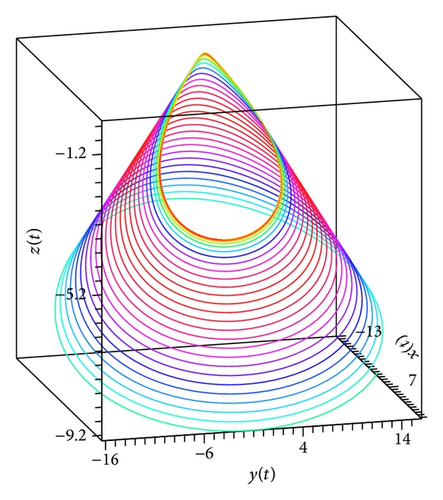
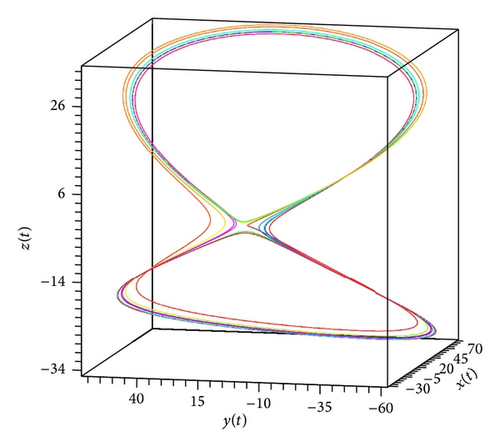
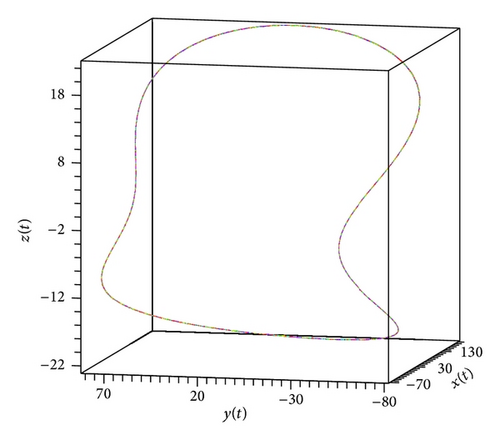
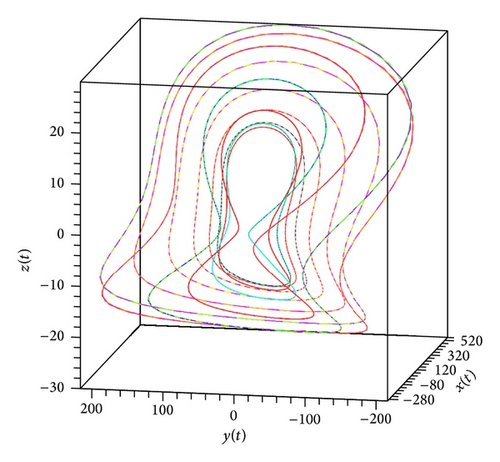
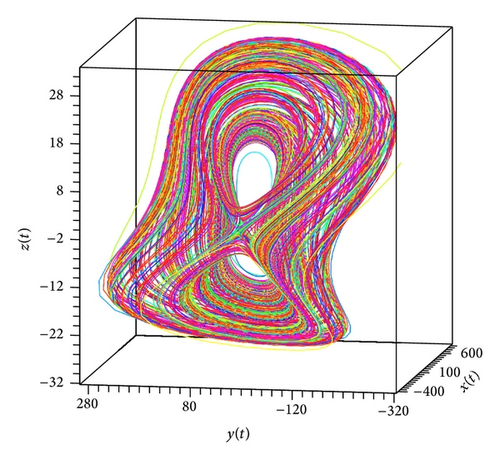
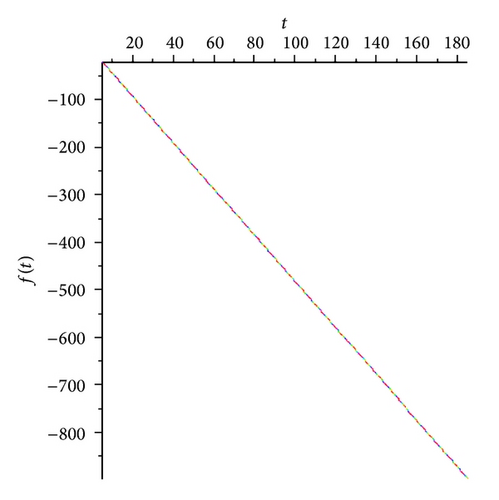
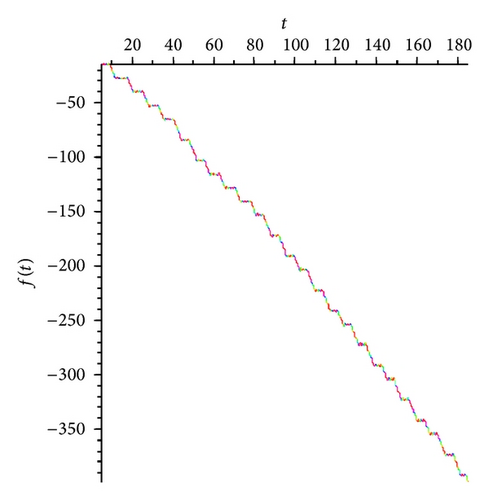
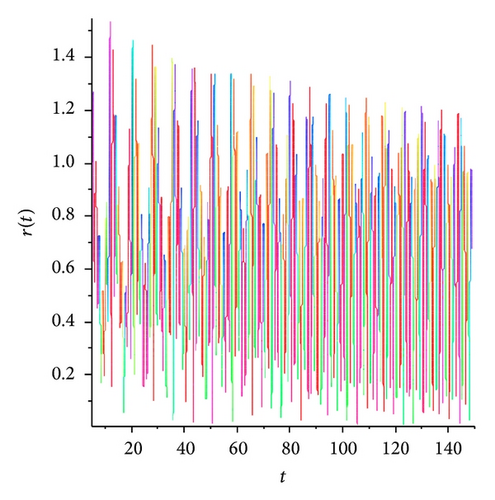
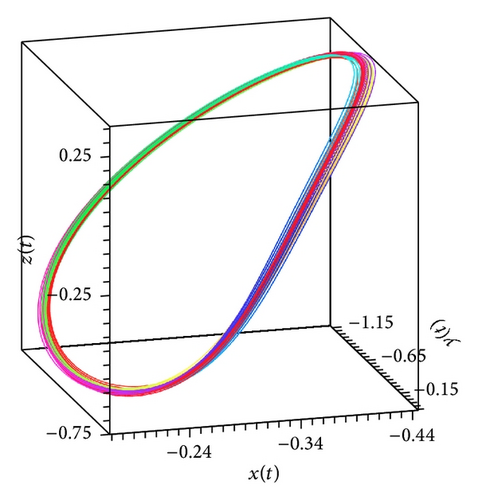
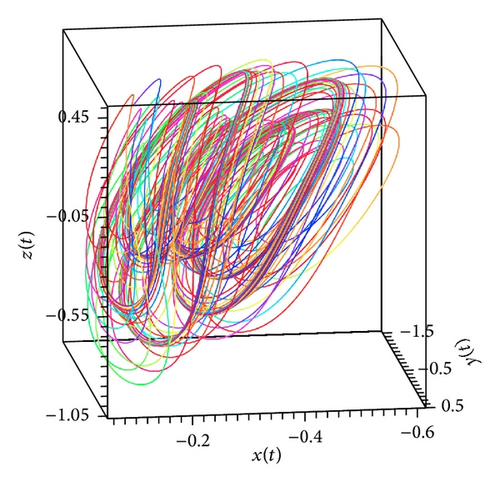
We note that Theorem 1 was the basic result of [17, 18]. In the present work, for the systems of type (19), substantial strengthening of Theorem 1 was got. The point is that condition (12) is not constructible. Nevertheless, if, for the proof of the state of chaos for system (19), we will use new theorems (Theorems 3, 4, and 5), then the verification of condition (12) can be ignored.

In addition, we did not begin to write the value of coefficients of system (19) (different from classic) at which in this system there is the Lorentz attractor. Researches of this attractor in detail are described in numerous articles and books.

Competing Interests

The author declares that are no competing interests regarding the publication of this paper.

References

1 Balibrea F., Caraballo T., Kloeden P. E., and Valero J., Recent developments in dynamical systems: three perspectives, International Journal of Bifurcation and Chaos in Applied Sciences and Engineering. (2010) 20, no. 9, 2591–2636, https://doi.org/10.1142/s0218127410027246, MR2738722, 2-s2.0-77956619894.
10.1142/s0218127410027246
Web of Science® Google Scholar
2 Feudel U., Complex dynamics in multistable systems, International Journal of Bifurcation and Chaos in Applied Sciences and Engineering. (2008) 18, no. 6, 1607–1626, https://doi.org/10.1142/s0218127408021233, MR2445231, 2-s2.0-51149083685.
10.1142/s0218127408021233
Web of Science® Google Scholar
3 Askar S. S., Karawia A. A., and Alshamrani A., Image encryption algorithm based on chaotic economic model, Mathematical Problems in Engineering. (2015) 2015, 10, 341729, https://doi.org/10.1155/2015/341729, 2-s2.0-84922375217.
10.1155/2015/341729
Web of Science® Google Scholar
4 Yao M., Zhang W., and Wang D. M., Modeling and chaotic dynamics of the laminated composite piezoelectric rectangular plate, Mathematical Problems in Engineering. (2014) 2014, 19, 345072, https://doi.org/10.1155/2014/345072, MR3179007, 2-s2.0-84896962111.
10.1155/2014/345072
Web of Science® Google Scholar
5 Idris R., Siri Z., and Hashim I., On a five-dimensional chaotic system arising from double-diffusive convection in a fluid layer, Abstract and Applied Analysis. (2013) 2013, 10, 428327, https://doi.org/10.1155/2013/428327, MR3035220.
10.1155/2013/428327
Google Scholar
6 Xie C., Xu Y., and Tong D., Chaos synchronization of financial chaotic system with external perturbation, Discrete Dynamics in Nature and Society. (2015) 2015, 7, 731376, https://doi.org/10.1155/2015/731376, MR3337404, 2-s2.0-84928473675.
10.1155/2015/731376
Web of Science® Google Scholar
7 Wang L., 3-scroll and 4-scroll chaotic attractors generated from a new 3-D quadratic autonomous system, Nonlinear Dynamics. (2009) 56, no. 4, 453–462, https://doi.org/10.1007/s11071-008-9417-4, MR2501159, 2-s2.0-67349148897.
10.1007/s11071-008-9417-4
Web of Science® Google Scholar
8 El-Dessoky M. M., Yassen M. T., Saleh E., and Aly E. S., Existence of heteroclinic and homoclinic orbits in two different chaotic dynamical systems, Applied Mathematics and Computation. (2012) 218, no. 24, 11859–11870, https://doi.org/10.1016/j.amc.2012.05.048, MR2945189, 2-s2.0-84863784924.
10.1016/j.amc.2012.05.048
Web of Science® Google Scholar
9 Bao J. and Yang Q., A new method to find homoclinic and heteroclinic orbits, Applied Mathematics and Computation. (2011) 217, no. 14, 6526–6540, https://doi.org/10.1016/j.amc.2011.01.032, MR2773240, 2-s2.0-79952008631.
10.1016/j.amc.2011.01.032
Web of Science® Google Scholar
10 Leonov G. A., Shilnikov chaos in Lorenz-like systems, International Journal of Bifurcation and Chaos in Applied Sciences and Engineering. (2013) 23, no. 3, 10, 1350058, https://doi.org/10.1142/s0218127413500582, MR3047973, 2-s2.0-84876204093.
10.1142/s0218127413500582
Web of Science® Google Scholar
11 Yang Q., Wei Z., and Chen G., An unusual 3D autonomous quadratic chaotic system with two stable node-foci, International Journal of Bifurcation and Chaos in Applied Sciences and Engineering. (2010) 20, no. 4, 1061–1083, https://doi.org/10.1142/S0218127410026320, MR2660159, 2-s2.0-77954210201.
10.1142/S0218127410026320
CAS Web of Science® Google Scholar
12 Chen Z., Yang Y., and Yuan Z., A single three-wing or four-wing chaotic attractor generated from a three-dimensional smooth quadratic autonomous system, Chaos, Solitons & Fractals. (2008) 38, no. 4, 1187–1196, https://doi.org/10.1016/j.chaos.2007.01.058, MR2435612, 2-s2.0-45849103151.
10.1016/j.chaos.2007.01.058
Web of Science® Google Scholar
13 Qi G., Chen G., van Wyk M. A., van Wyk B. J., and Zhang Y., A four-wing chaotic attractor generated from a new 3-D quadratic autonomous system, Chaos, Solitons and Fractals. (2008) 38, no. 3, 705–721, https://doi.org/10.1016/j.chaos.2007.01.029, MR2423359, 2-s2.0-43049125173.
10.1016/j.chaos.2007.01.029
Web of Science® Google Scholar
14 Vahedi S. and Noorani M. S. M., Analysis of a new quadratic 3D chaotic attractor, Abstract and Applied Analysis. (2013) 2013, 7, 540769, https://doi.org/10.1155/2013/540769, MR3055958.
10.1155/2013/540769
Google Scholar
15 Wang X. and Chen G., A gallery of Lorenz-like and Chen-like attractors, International Journal of Bifurcation and Chaos in Applied Sciences and Engineering. (2013) 23, no. 4, 20, 1330011, https://doi.org/10.1142/s0218127413300115, MR3063354, 2-s2.0-84877951071.
10.1142/s0218127413300115
Web of Science® Google Scholar
16 Onma O. S., Olusola O. I., and Njah A. N., Control and synchronization of chaotic and hyperchaotic Lorenz systems via extended backstepping techniques, Journal of Nonlinear Dynamics. (2014) 2014, 15, 861727, https://doi.org/10.1155/2014/861727.
10.1155/2014/861727
Google Scholar
17 Belozyorov V. Y., Exponential-algebraic maps and chaos in 3D autonomous quadratic systems, International Journal of Bifurcation and Chaos in Applied Sciences and Engineering. (2015) 25, no. 4, 24, 1550048, https://doi.org/10.1142/s0218127415500480, MR3342108, 2-s2.0-84929207413.
10.1142/s0218127415500480
Web of Science® Google Scholar
18 Belozyorov V., Research of chaotic dynamics of 3D autonomous quadratic systems by their reduction to special 2D quadratic systems, Mathematical Problems in Engineering. (2015) 2015, 15, 271637, https://doi.org/10.1155/2015/271637, MR3332159, 2-s2.0-84927142918.
10.1155/2015/271637
Web of Science® Google Scholar
19 Belozyorov V. Y., Invariant approach to existence problem of chaos in 3D autonomous quadratic dynamical systems, International Journal of Bifurcation and Chaos in Applied Sciences and Engineering. (2016) 26, no. 1, 14, 1650012, https://doi.org/10.1142/s0218127416500127, MR3462182, 2-s2.0-84959161444.
10.1142/s0218127416500127
Web of Science® Google Scholar

All articles

Chaos in Essentially Singular 3D Dynamical Systems with Two Quadratic Nonlinearities

Abstract

1. Introduction

2. Bounded Solutions of Quadratic Dynamical Systems

3. Definition of Essentially Singular 3D Dynamical Systems

4. Lorenz-Like Systems

5. Examples

6. Conclusion

Competing Interests

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Chaos in Essentially Singular 3D Dynamical Systems with Two Quadratic Nonlinearities

Abstract

1. Introduction

2. Bounded Solutions of Quadratic Dynamical Systems

3. Definition of Essentially Singular 3D Dynamical Systems

4. Lorenz-Like Systems

5. Examples

6. Conclusion

Competing Interests

References

Figures

References

Related

Information