The solution of the field equations of the conformal theory of gravitation with Dirac scalar field in Cartan-Weyl spacetime at the very early Universe is obtained. In this theory dark energy (described by an effective cosmological constant) is a function of the Dirac scalar field β. This solution describes the exponential decreasing of β at the inflation stage and has a limit to a constant value of the dark energy at large time. This can give a way to solving the fundamental cosmological constant problem as a consequence of the fields dynamics in the early Universe.

1. Introduction

The Poincaré-Weyl gauge theory of gravitation (PWTG) has been developed in [1]. This theory is invariant concerning both the Poincare subgroup and the Weyl subgroup—extensions and compressions (dilatations) of spacetime. Dilatations are equivalent in the mathematical sense to the transformations of the group of length calibres changes, which is the gauge group of the Weyl theory developed in 1918 [2]. The gauge field introduced by the subgroup of dilatations is named as dilatation field. Its vector potential is the Weyl vector, and its strength is Weyl’s segmental curvature tensor arising in the geometrical interpretation of the theory together with the curvature and torsion tensors. The dilatation gauge field does not coincide with electromagnetic field (that has been asserted by Weyl in his basic work [2]) but represents a field of another type [3]. In particular, quanta of this field can have nonzero rest masses.

As it has been shown in [1], an additional scalar field β(x) is introduced in PWTG as an essential geometrical addendum to the metric tensor. The properties of this field coincide with those of the scalar field introduced by Dirac in his well-known article [4] and also by Deser in [5]. We will name this field as Dirac scalar field. The Dirac scalar field plays an important role in construction of the gravitation Lagrangian, some members of which have structure of the Higgs Lagrangian and after spontaneous braking of dilatational invariance can cause an appearance of nonzero rest masses of particles [6].

On the basis of the observational data, it is accepted in modern cosmology that the dark energy (described by the cosmological constant) is of dominant importance in dynamics of the Universe. In this connection the major unsolved problem of modern fundamental physics is very large difference of around 120 orders of magnitude between a very small value of Einstein cosmological constant Λ, which can be estimated on the basis of modern observations in cosmology, and the value of the cosmological constant in the early Universe, which has been estimated by theoretical calculations in quantum field theory of quantum fluctuation contributions to the vacuum energy [7–10]. In the present work we try to understand the cosmological constant problem as the effect of the gravitational field and the Dirac scalar field dynamics in the Cartan-Weyl spacetime in the early Universe.

2. Gravitational Lagrangian

Spacetime in PWTG has the geometrical structure of the Cartan-Weyl space with a curvature 2-form , a torsion 2-form , and a nonmetricity 1-form of the Weyl type, , where is a Weyl 1-form.

On the basis of PWTG, a conformal theory of gravitation in Cartan-Weyl spacetime with the Dirac scalar field has been developed in the external form formalism with the Lagrangian density 4-form

[11–13]:

()

where

is the matter Lagrangian density 4-form and Λ^ab are the Lagrange multipliers and the gravitational field Lagrangian density 4-form

reads:

()

Here ∧ is the exterior product sign, d is the exterior derivative operator, and * is the Hodge dual conjugation. The second term in (2) is the effective cosmological constant which is interpreted as the dark energy density (Λ is the Einstein cosmological constant).

Variational field equations in the Cartan-Weyl spacetime have been derived from by exterior form variational formalism [14]. Independent variables are basis 1-form θ^a, a nonholonomic connection 1-form , the scalar field β, and Lagrange multipliers Λ^ab. As a result we have Γ-, θ-, and β-equations, which have the following forms in vacuum () [11–13]:

Γ-equation:

()

θ-equation:

()

β-equation:

()

The variation with respect to the Lagrange multipliers Λ^ab gives the Weyl condition for the nonmetricity 1-form

()

3. Solutions of the Field Equations at Ultra-Early Universe

We will solve the field equations for the scale factor a(t) and the scalar Dirac field β at the very early stage of evolution of Universe, when a matter density has been very small, . We will omit the terms quadratic in curvature for simplicity.

In homogeneous and isotropic spacetime the conditions are valid, and we will find, as the consequence of the field equations, the torsion and nonmetricity in the forms, , , where the coefficients χ_T, χ_Q are expressed by couple constants of Lagrangian density (2) (see the Appendix).

We consider the spatially flat Friedmann-Robertson-Walker (FRW) metric:

()

Taking into account that

, we obtain from the θ-equation together with the β-equation the following system of equations [11–13]:

()

where the constants A, B, B₃ = (1/3)(2B₁ + B₂), B₁, and B₂ are expressed through the parameters of Lagrangian density (2), the components (2, 2) and (3, 3) being equal to the component (1, 1).

The system of (8)–(10) is inconsistent, because we have three equations for two unknown functions a(t) and β(t). Let us put in this system B₁ = B₂ = B₃ = 1 and also u = ln⁡a, v = ln⁡β. Then subtract (8) from (10). As a result we obtain the following system of equations:

()

Equation (11) is equivalent to the equation

()

It is easy to check that (12) is fulfilled identically as a consequence of (14). Therefore we have only 2 equations (13) and (14) for 2 unknown functions a(t), β(t), and this system of equations is consistent. In what follows we choose the sign “+” in (14).

Let us find

from (14) and put it in (13). We obtain the equation

()

The first integral of this equation is the following:

()

where λ₀ is a constant of integration.

The system of (14), (16) has a large variety of integrable solutions parameterized by ω and λ₀. Let us obtain the solution for the case ω = 0. If we put in (16) λ₀ = λ, then this equation reads,

, and we have a solution [13]

()

We assume that the value of β is very large, when t = 0. Therefore the constant of integration t₀ should be very small (0 < t₀ ≪ λ⁻¹). Then from (17) under t ≫ t₀ one has approximately

()

These solutions realize exponential diminution of a field β (see Figure 1 for function (17)), and thus sharp exponential decrease of physical vacuum energy (dark energy) by many orders. We have β → 1, Λ_eff = β²Λ → Λ in a limit at t → ∞. Thus, the effective cosmological constant can slightly differ already by the end of inflation from the limiting value equal to its modern size Λ that provides the subsequent transition from the Friedmann epoch to the epoch of the accelerated expansion in accordance with the modern observed cosmological data.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Solution (17) for the Dirac scalar field in the early Universe.

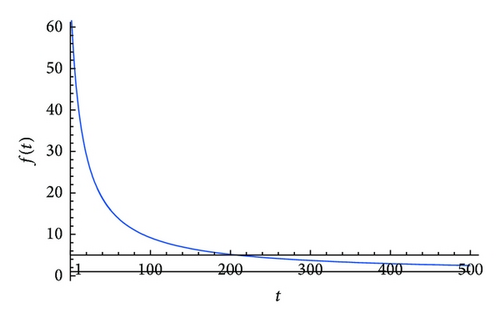
Our solutions are realized, if the conditions are valid, B = 3A, B₁ = 1, and B₂ = 1. These conditions are determined in rather complicated manner by the 16 coupling constants of gravitational Lagrangian density (2) and can be easily fulfilled (see the Appendix).

4. Discussion and Final Remarks

Here the field equations for the spatially flat homogeneous and isotropic ultra-early Universe are investigated and the solution for the Dirac scalar field (and therefore for the effective cosmological constant) is found. This solution for the scalar field has the behavior of the very extensive diminishing exponent, whose limits are the modern value of the Einstein cosmological constant. Solution (17) could be realized at the very beginning of the Universe evolution, when the cosmological constant Λ₀ estimated by quantum field theory was equal to , and the number β₀ ~ 10⁶⁰ was very large.

Thus our result can explain the exponential decrease in time at very early Universe of the dark energy (the energy of physical vacuum), described by the effective cosmological constant. This can give a way to solving the problem of cosmological constant as a consequence of fields dynamics at the early Universe. It is well known that this problem is one of the fundamental problems of the modern theoretical physics [7–10].

We point out that the ultra-rapid decrease of the energy of physical vacuum according to law (17) occurs only prior to the Friedmann era evolution of the Universe. Further evolution of the Universe is determined not only by a scalar field only but also by the born ultra-relativistic matter and the radiation interacting with it.

The Dirac scalar field condenses near massive objects. As a consequence of this, the authors formulate the hypothesis that the Dirac scalar field is realized itself not only as the “dark energy” but also as one of the components of the “dark matter” [13].

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgment

The results were obtained within the framework of performance of the State Task number 3.1968.2014/K of the Ministry of Education and Science of the Russian Federation.

Appendix

Let us show how the conditions B₁ = B₂ = 1 can be fulfilled.

As a consequence of the Γ-equation, taking into account that

for metric (7) (see [15]), we have the following equalities:

()

We can put , , as a consequence of (A.1).

Let us choose for the coupling constants of Lagrangian density (2) the values l₂ = 2, l₃ = 0, and ζ = 0 for simplicity. Then we have from equalities (A.1)

()

Now let us put the results obtained into the θ- and β-equations and get the system of (8)–(10) with

()

Let us put the value

. Then we have

()

As a consequence, the following system of equations is obtained from (A.3):

()

If we put now B₁ = B₂ = 1, then we obtain

()

Therefore we can conclude from (2) that the Dirac scalar field β is the physical field, but the Weyl 1-form

is tachyonic.

It is also easy to satisfy the condition ω = B/A − 3 = 0. We have

()

If we put now ρ₁ = 0 for simplicity, then we obtain ρ₂ ≈ −0.5, with the values of the coupling constants chosen and calculated before.

References

1 Babourova O. V., Frolov B. N., and Zhukovsky V. Ch., Gauge field theory for the Poincaré-Weyl group, Physical Review D. (2006) 74, no. 6, 12, 064012, https://doi.org/10.1103/PhysRevD.74.064012.
10.1103/PhysRevD.74.064012
Web of Science® Google Scholar
2 Weyl H., Space-Time-Matter, 1952, Dover Publications, New York, NY, USA.
Google Scholar
3 Utiyama R., On Weyl′s gauge field, Progress of Theoretical Physics. (1973) 50, 2080–2090, https://doi.org/10.1143/PTP.50.2080, MR0426710.
10.1143/PTP.50.2080
Google Scholar
4 Dirac P. A., Long range forces and broken symmetries, Proceedings of the Royal Society. (1973) 333, 403–418, https://doi.org/10.1098/rspa.1973.0070, MR0329542.
10.1098/rspa.1973.0070
Google Scholar
5 Deser S., Scale invariance and gravitational coupling, Annals of Physics. (1970) 59, no. 1, 248–253, https://doi.org/10.1016/0003-4916(70)90402-1, MR0261924, 2-s2.0-0000931656.
10.1016/0003-4916(70)90402-1
Web of Science® Google Scholar
6 Frolov B. N., P. Pronin and G. Sardanashvily, Generalized conformal invariance and gauge theory of gravity, Gravity, Particles and Space-time, 1996, World Scientific, Singappore, 113–144.
10.1142/9789812830180_0008
Google Scholar
7 Weinberg S., The cosmological constant problem, Reviews of Modern Physics. (1989) 61, no. 1, 1–23, MR977942, https://doi.org/10.1103/revmodphys.61.1.
10.1103/RevModPhys.61.1
CAS Web of Science® Google Scholar
8 Peebles P. J. E. and Ratra B., The cosmological constant and dark energy, Reviews of Modern Physics. (2003) 75, no. 2, 559–606, https://doi.org/10.1103/revmodphys.75.559, MR1973358.
10.1103/RevModPhys.75.559
CAS Web of Science® Google Scholar
9 Padmanabhan T., Cosmological constant—the weight of the vacuum, Physics Reports. (2003) 380, no. 5-6, 235–320, 2-s2.0-0038457945, https://doi.org/10.1016/s0370-1573(03)00120-0, MR1992680.
10.1016/S0370-1573(03)00120-0
Web of Science® Google Scholar
10 Li M., Li X.-D., Wang S., and Wang Y., Dark energy, Communications in Theoretical Physics. (2011) 56, no. 3, 525–560, https://doi.org/10.1088/0253-6102/56/3/24.
10.1088/0253-6102/56/3/24
CAS Web of Science® Google Scholar
11 Babourova O. V., Frolov B. N., and Lipkin K. N., Gravitation theory with a Dirac scalar field in the exterior form formalism and the cosmological constant problem, Gravitation and Cosmology. (2012) 18, no. 4, 225–231, https://doi.org/10.1134/s0202289312040032, MR3002660, 2-s2.0-84870684429.
10.1134/S0202289312040032
Web of Science® Google Scholar
12 Babourova O. V., Lipkin K. N., and Frolov B. N., Theory of gravity with the Dirac scalar field and the problem of cosmological constant, Russian Physics Journal. (2012) 55, no. 7, 855–857, https://doi.org/10.1007/s11182-012-9891-5, 2-s2.0-84871105104.
10.1007/s11182-012-9891-5
Web of Science® Google Scholar
13 Babourova O. V. and Frolov B. N., Mathematical Foundations of The Modern Theory of Gravitation, 2012, MPGU, Moscow, Russia, (Russian).
Google Scholar
14 Babourova O. V., Frolov B. N., and Klimova E. A., Plane torsion waves in quadratic gravitational theories in Riemann-Cartan space, Classical and Quantum Gravity. (1999) 16, no. 4, 1149–1162, https://doi.org/10.1088/0264-9381/16/4/005, MR1696145, 2-s2.0-0033433533.
10.1088/0264-9381/16/4/005
CAS Web of Science® Google Scholar
15 Babourova O. V. and Frolov B. N., Matter with dilaton charge in Weyl-Cartan spacetime and evolution of the universe, Classical and Quantum Gravity. (2003) 20, no. 8, 1423–1441, https://doi.org/10.1088/0264-9381/20/8/302, MR1979066.
10.1088/0264-9381/20/8/302
Web of Science® Google Scholar

Citing Literature

All articles

Dark Energy as a Cosmological Consequence of Existence of the Dirac Scalar Field in Nature

Abstract

1. Introduction

2. Gravitational Lagrangian

3. Solutions of the Field Equations at Ultra-Early Universe

4. Discussion and Final Remarks

Conflict of Interests

Acknowledgment

Appendix

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Dark Energy as a Cosmological Consequence of Existence of the Dirac Scalar Field in Nature

Abstract

1. Introduction

2. Gravitational Lagrangian

3. Solutions of the Field Equations at Ultra-Early Universe

4. Discussion and Final Remarks

Conflict of Interests

Acknowledgment

Appendix

References

Citing Literature

Figures

References

Related

Information