To minimize the cost and maximize the ease of use, a class of dual-spin mortars is designed which only rely on GPS receiver and geomagnetic measurements. However, there are some problems to be solved when the range is small, such as low correction authority and trajectory bending. Guidance law design for this mortar is detailed. Different guidance laws were designed for the ascending and descending segments, respectively. By taking variable parameter guidance law in the vertical plane and using compensation in the lateral plane, the problems mentioned above were resolved. Roll angle resolving algorithms with geomagnetic measurements were demonstrated and the experiment results proved to be effective. In order to verify the effectiveness, Seven-Degrees-of-Freedom (7-DOF) rigid ballistic model were established and hardware in the loop simulation was introduced. After the transform function of the actuator was obtained, the control model of the shell was improved. The results of the Monte Carlo simulation demonstrate that the guidance law is suitable and the mortar can be effectively controlled.

1. Introduction

In the last few decades, autonomous guidance of mortar ammunitions has become a battlefield reality. Field-ready systems include the Israeli/Raytheon 120 GM DAGGER, Lockheed Martin’s M396 PGMM, and General Dynamics’s 81 mm air-dropped version. All these ammunitions use control surfaces for trajectory shaping and have onboard Inertial Measuring Unit (IMU), thus making them have a very high production cost per round [1–5]. New concepts are necessary to be designed to reduce the costs.

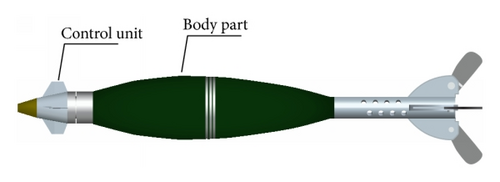
A new concept for guided mortars is proposed in this paper. The mortar takes dual-spin configuration and has forward mounted fixed canards [6, 7], resembling Precision Guidance Kit (PGK), as shown in Figure 1. But the IMUs are removed, leaving only Global Position System (GPS) receiver and geomagnetic measurements. The GPS receiver provides velocity and position information for the onboard computer, and the geomagnetic measurements furnish the computer with the roll angle position of the fixed canards. Several researchers pointed out that GPS can be jammed and can provide sufficient precision [1, 2], but the question is the following: could such a design be effectively controlled?

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

A new concept guided mortars.

For the new concept guided mortars, if the range to the target is small, for example, 2 km, small muzzle velocity and large firing angle are needed [8]. But at the ballistic vertex, the velocity of mortar is small, just about 50 m/s, and the trajectory bends greatly, which brings low correction authority and adds difficulty in the guidance design [9, 10].

This paper dealt with the guidance law design for a class of dual-spin mortars. The key problems of design are proposed in Section 2. The guidance law was designed in Section 3. Roll angle resolving algorithms with geomagnetic measurements were stated in Section 4. Hardware in the loop simulation was introduced in Section 5. Finally, conclusions were presented in Section 6.

2. Guidance Package and Problem Formulation

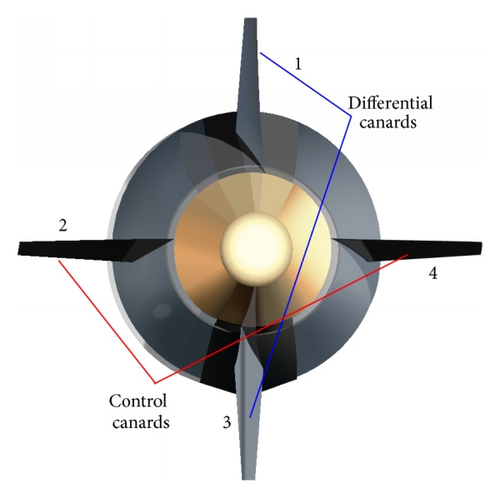
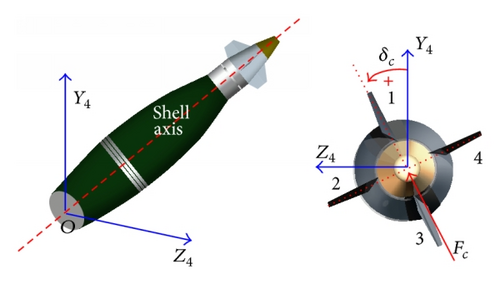
On the front part of the mortar, the guidance kit has two sets of fixed canards. The two pairs of canard fins are all at fixed angle of cant (about 4°) and are assembled in a unit which rotates about the shell axis by the aerodynamic moment or the actuator. One pair of canards of the opposite cant angle are used to generate rolling moment in a direction opposite to that of the shell which could cause the canard to rotate in reverse direction against the shell, called differential canards, and the other of the same cant angle aims at emerging control moment and correcting the trajectory, called controlled canards. The direction of rotation of canard fins and shell have been identified in Figure 2. A distinct view of canard fins frame is shown in Figure 3. The GPS receiver in the head gets the velocity and position information, and the geomagnetic sensors can provide the roll angle position of fixed canards. All these data are sent to the onboard computer, and the computer gives control commands to make the guidance kit stay in the corresponding roll angle to achieve trajectory correction.

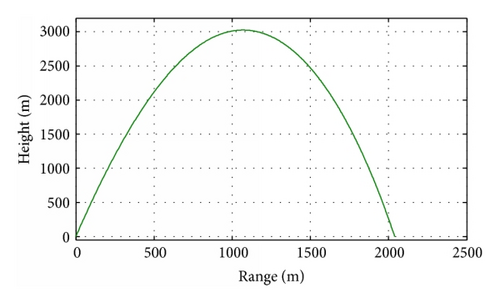
For a small range, the muzzle velocity is small and the firing angle is large. The performance of range 2 km is shown in Figures 4–7. The firing angle is 80° and the muzzle velocity is 278 m/s. Small velocity induces small aerodynamic force of the canards, especially at the ballistic vertex, and the correction authority reduces a lot. Furthermore, the trajectory curvature is little, and the conventional proportional guidance cannot be used in the above-mentioned case.

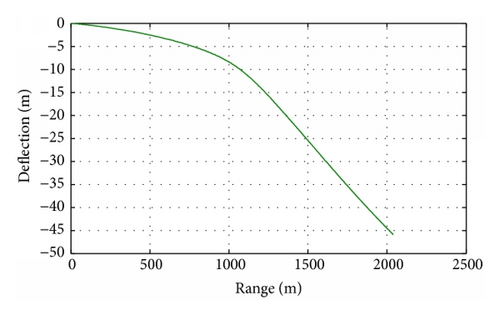
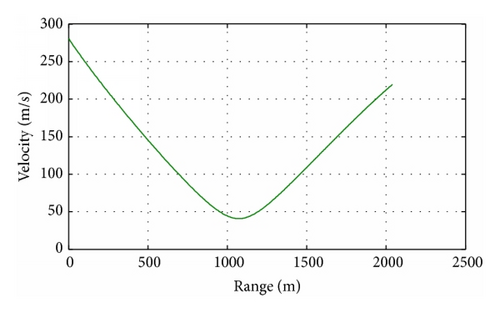
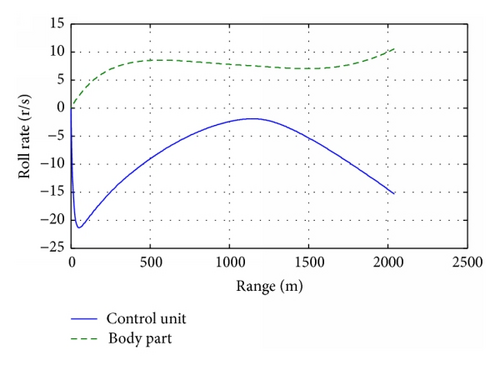
One major challenge is the lack of control authority. Because of low velocity, the fixed canards can provide limited aerodynamic force to correct the trajectory. The winds, launch disturbance, parameter perturbation, and uncertainties in geodetics, coupled with variation in projectile mass, all result in the trajectory change and make the impact points depart from the target. Using the limited control authority to make the shell shoot straight on the target is one of the key problems.

The other challenge is the trajectory curvature. If conventional proportional guidance law is used, the proportion parameter cannot be suitable along the trajectory, because the curvature is little, and the shell cannot turn sharply due to limited control authority. In other words, conventional proportional guidance law cannot cooperate well with the mortar of the above present guidance kit. So a suitable guidance law is needed.

The main purpose of this paper is to overcome the challenges and to design suitable guidance law for the dual-spin mortars.

3. Guidance Law Design

The new concept dual-spin mortars are used to attack static targets. This mission can be decomposed into two segments, ascending segment and descending segment. Lateral correction is conducted in the ascending segment, and comprehensive correction is taken in the descending segment.

In the following sections, 7-DOF rigid ballistic model was established, and the advanced guidance law in the ascending segment and the descending segment was designed [11–13].

3.1. 7-DOF Rigid Ballistic Model

In the flight, the two parts of the projectile spin in different directions due to the effort of the aerodynamic forces (as shown in Figure 2). In order to describe the motion of the projectile, three translational and four rotational rigid body degrees of freedom are introduced, that is, the 7-DOF rigid ballistic model. The translational degrees of freedom are the three components of the mass center position vector. The rotational degrees of freedom are the Euler yaw and pitch angles as well as roll angle of the guidance kit and that of the shell.

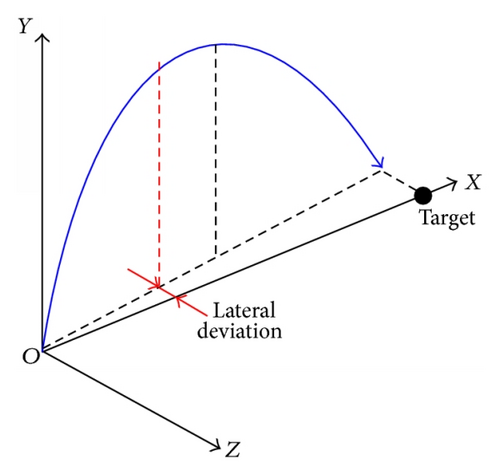
Guidance law is aiming at gaining proper and valid control command. The control signal comes from the deviation between the desired trajectory and the current one. To reasonably describe the relative position between ideal ballistic curve and the real one, the inertial reference frame Oxyz is introduced, as shown in Figure 8. The positive X-axis is in the longitudinal plane and pointed to the target. The positive Y-axis is the vertical plane and pointed to the up direction. The positive Z-axis, normal to the Oxy plane, is pointed to the right.

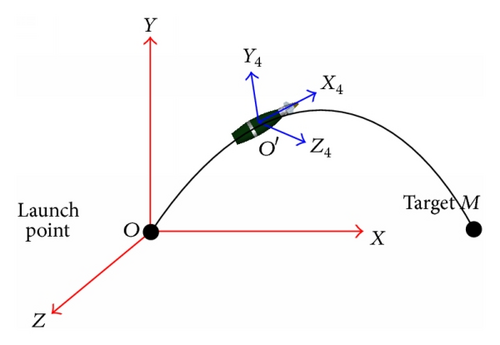
The quasi body reference frame O^′x₄y₄z₄ is introduced to describe the rotational motion, and the sequence of rotation from the inertial frame Oxyz is pitch φ, yaw ψ. The O^′x₄y₄ plane of the quasi body reference frame is fixed in the vertical plane, so it is convenient to be shared by the guidance kit and the shell (Figure 9).

Equations (1) and (2) represent the translational and rotational kinematic and dynamic equations of motion for a dual-spin projectile. Both sets of translational equations are expressed in the inertial frame:

()

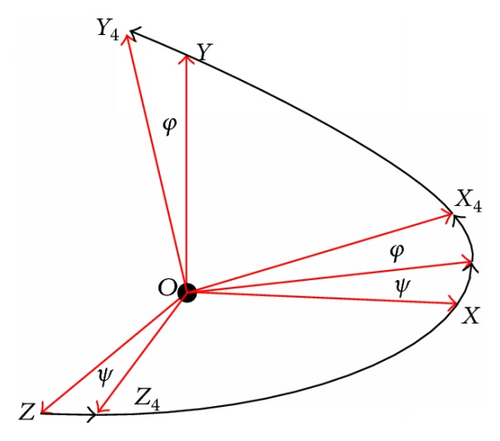
F_x, F_y, and F_z are components of the total force expressed in the inertial frame Oxyz. v_x, v_y, and v_z are velocity vector components of the composite center of mass expressed in the inertial frame Oxyz. x, y, and z are position vector components of the composite center of mass expressed in the inertial frame Oxyz. ω_y4 and ω_z4 are components of the angular velocity vector expressed on the Y₄-axis and Z₄-axis of the quasi body reference frame O^′x₄y₄z₄.

The two rotational equations are expressed in the quasi body reference frame:

()

M_xf, M_x, M_y, and M_z are components of the total moment of both the guidance kit and the shell expressed on the x-axis of the quasi body reference frame. γ_f and γ_a are roll angles of the guidance kit and the shell. ψ and φ are yaw angle and pitch angle, respectively.

Loads on the composite projectile body are due to weight and aerodynamic forces. All the aerodynamic coefficients are acquired by numerical computing. The forces and moments are present as follows:

()

Note that the force vector

presents the components of aerodynamic forces in the quasi body reference frame, and it should be transformed to the inertial frame in practical application. M_fa and M_af are the frictional moments between the guidance kit and the shell when they rotate in relation to each other. The frictional moments can be computed as follows:

()

where c_f is the equivalent damping coefficient induced by spin friction.

The longitudinal and lateral aerodynamic angles of attack are computed as follows:

()

If the mortar is under control condition, the guidance kit is set to a certain rotating angle. So the control equation can be acquired and shown as follows:

()

where γ_s is the control angle computed from the control algorithm.

3.2. Lateral Correction in the Ascending Segment

In the ascending segment, only the lateral deviation is corrected, which is caused by winds, launch disturbance, parameter perturbation, and so on. Without IMUs, only GPS information, the position vector components , and the velocity vector components can only be provided. As a consequence, the traditional proportional guidance law is invalid, and the advanced proportional guidance law is needed.

On the basis of relative position shown in Figure 10, the lateral deviation in the ascending segment can be denoted by the distance Z that the projectile is away, departed from gun-target connecting line, in other words, the X-axis in the inertial reference frame. For lateral deviation, the significant influence factors can be attributed to lateral position and velocity. With respect to lateral correction, consequently, the components of the position vector and velocity vector need to be considered. The guidance law for the ascending segment should take the trajectory characteristic into consideration, and the advanced lateral proportional guidance law is employed.

With the advanced lateral proportional guidance law, the lateral guidance signal is calculated as follows:

()

where Z and V_z are the components of position vector and velocity vector on the Z-axis, respectively, k_z is the weight parameters of Z, and k_vz is the weight parameters of V_z.

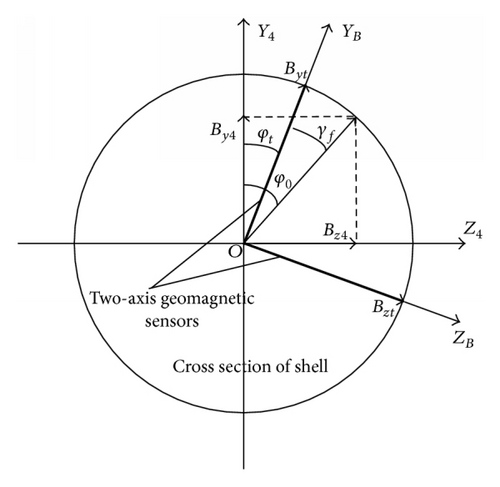
Reference [3] pointed out that the control response had the same direction with the control force for fin-stabilized projectiles. In the canard guidance kit, the aerodynamic control force F_c originates from control canards. In the unguided trajectories, the kit rotates about the shell axis and the control force can be canceled out in a cycle. But if the control canard fins maintain in a specific position, the specific force F_c can be conducted in a specific direction. This direction is called the phase angle δ_c in this paper, where the normal axis of the control canard face (fins 2 and 4) should stay on. The δ_c is defined as shown in Figure 11. This Coordinate System O^′x₄y₄z₄ is defined in cross section of the shell normal to the shell axis. The positive Y₄-axis is in the vertical plane and point to the up direction. The positive Z₄-axis, normal to the Y₄-axis, is pointing to the right. The positive phase angle δ_c is spinning clockwise.

So the control signal of the actuator, phase angle δ_c, can be given as follows:

()

That is to say, if the absolute value of S_z is not larger than 10, the shell is under no control condition. If S_z is larger than 10, the roll angle of the guidance kit is to set 90°, and if S_z is smaller than −10, the roll angle is to set −90°.

3.3. Comprehensive Correction in the Descending Segment

In the descending segment, the trajectory is a smooth curve and pointing to the static target. According to trajectory characteristic and the guidance law advantage, proportional guidance law, therefore, is applied in the descending segment. Within the proportional guidance law, the lateral deviation and the longitudinal one are both corrected simultaneously. The deviations are obtained based on the angle relations as shown in Figure 12.

As comprehensive correction is conducted, proportional guidance is introduced:

()

where n_c is the acceleration command, V_c is the velocity of the shell reaching target,

is the angle rate of the Line of Sight (LOS), and N^′ is the proportion parameter. The motion of the mortar can be divided into motions in the vertical and lateral planes, and different guidance laws would be taken in the two planes. In the vertical plane variable parameter proportional guidance is taken for the purpose of dealing with trajectory bending. That is to say, N^′ takes different value along the trajectory. The value of N^′ is acquired by standard trajectory computing before shooting and can be got through interpolation. Trajectory curve is smooth in the lateral plane, and classical proportional guidance is used, where N^′ takes 4 as its value.

The wind distribution over the flight played an important role in trajectory error. The wind can be obtained from field meteorological measurement. For the purpose of reducing the wind disturbance, two methods are taken. Firstly, before standard trajectory is computed, the firing angle and azimuth angle need to be adjusted to make sure that the mortar can impact targets without correction directly. But when shooting, the azimuth angle can be aligned with the line between gun and target. Secondly, correction compensation can be added in the lateral plane. All the fin-stabilized projectiles have the same characteristic that have a left deflection without correction. For this reason, compensation is added to the lateral guidance signal:

()

where

takes −0.3 as its value. Based on the guidance law designed above, guidance control signals can be got as follows:

()

X_T, Y_T, and Z_T are components of the target position expressed in the inertial frame Oxyz. The subscripts v and l are on behalf of the parameters in vertical and lateral planes, respectively. Then the control signal of the actuator can be acquired:

()

3.4. Simulation Results

The guidance law designed above was implemented in simulations, and 7D rigid ballistic model [4] was applied, along with rudimentary models of the GPS and geomagnetic model. The model of the actuator was not introduced, because this section aimed at the effectiveness of the guidance law.

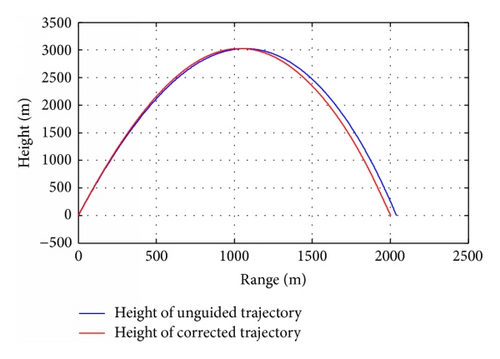
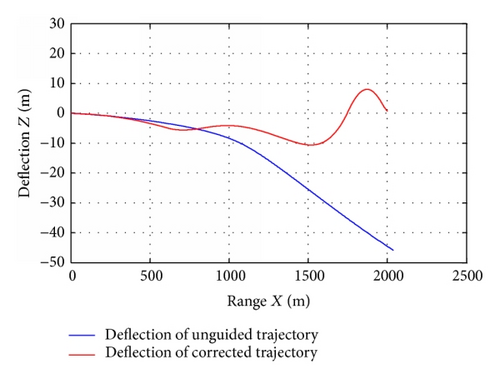
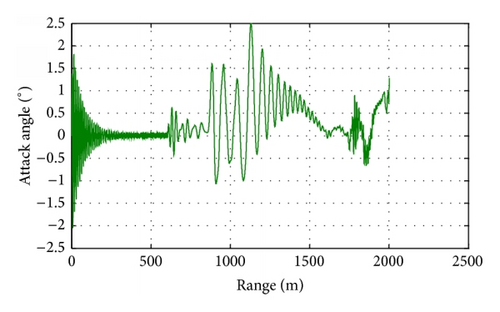
Figures 13–16 show the trajectory characteristics of the mortar under control. In ascending segment, the mortar is under control from 600 m to 1000 m. Figures 13 and 14 show that the shell’s trajectory is corrected, and the deflection in the vertical and lateral planes reduces. Figures 15 and 16, respectively, give the attack angle variation and sideslip angle variation in the guided process. The control force consequentially causes the trajectory instability according to the suddenly aerodynamic force, which are generally revealed by the attack angle motion. So the attack angle can obviously indicate the control operation. But for lateral correction, the sideslip angle can well show the guidance action. For example, the sudden increase of sideslip angle in 600 m indicates the carrying out of lateral correction. In the descending segment, comprehensive correction is conducted. In the early stage correction in the vertical plane occupied the major, from 1 km to 1.5 km, and the lateral deflection increases. The reason is that major correction needs to be applied in the vertical plane to assure that the mortar axis aligns with the velocity, and the lateral deflection would change because of the vertical correction coupling interference. In the following stage of the descending segment, the lateral correction took most part along with the vertical deviation decrease. The target longitudinal and lateral errors were, respectively, 2.3 m and 0.57 m. That is to say, the guidance law is suitable and can effectively correct the trajectory errors caused by various disturbance and deviation.

4. Roll Angle Resolving with Geomagnetic Measurements

Without the IMUs, the roll angle is obtained by geomagnetic measurements. The two-axis geomagnetic senor must be assembled in the cross section of the guidance kit, which is perpendicular to projectile axis. As the range and ballistic height of mortars are both small, the change of geomagnetic components change are tiny, no more than 1%. The geomagnetic field can be regarded as invariable magnetic field and be acquired by International Geomagnetic Reference Field (IGRF) model.

4.1. Roll Angle Resolving Algorithm

From IGRF model, the geomagnetic field components (magnetic intensity T, magnetic declination D, and magnetic inclination I) are obtained. The components of geomagnetic field can be presented in the inertial frame Oxyz as follows:

()

So the components of geomagnetic field in the quasi body reference frame O^′x₄y₄z₄ can be acquired:

()

The relationship between the geomagnetic sensors and the components of geomagnetic field in the quasi body reference frame O^′x₄y₄z₄ is shown in Figure 17.

The roll angle of the guidance kit is calculated as follows:

()

4.2. Experiment Results

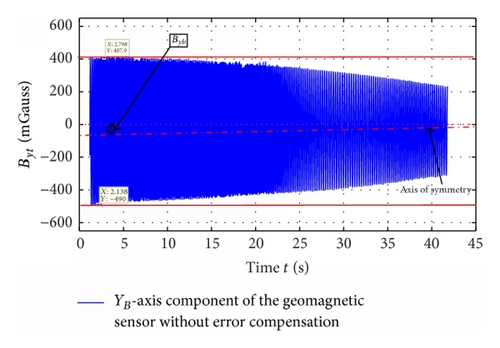
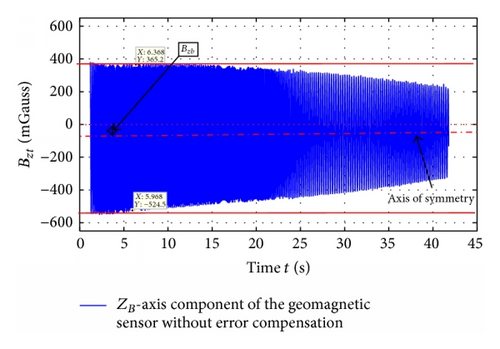
In order to verify the roll angle resolving algorithm, the experiment was conducted with the Nonmagnetic Three-Axis Turntable. The raw geomagnetic measurements are shown in Figures 18 and 19.

The geomagnetic sensor is in the cross section, which is perpendicular to projectile axis. As the mortar rotated around projectile axis, the components of geomagnetic sensor should change along sine signal with the axis of symmetry 0 mGauss. Therefore, the measurement error can be compensated by the online calibration, as follows:

()

B_yr and B_zr are the raw geomagnetic measurements; B_yb and B_zb are the compensations of Y_B-axis and Z_B-axis respectively, which can be computed by the online calibration in the flight, as shown in Figures 18 and 19. The corrected geomagnetic measurements are shown in Figures 20 and 21. The axis of symmetry is very close to 0 mGauss.

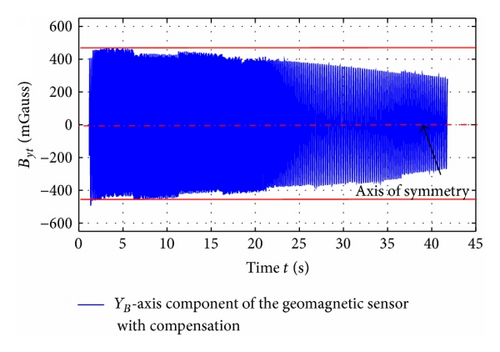
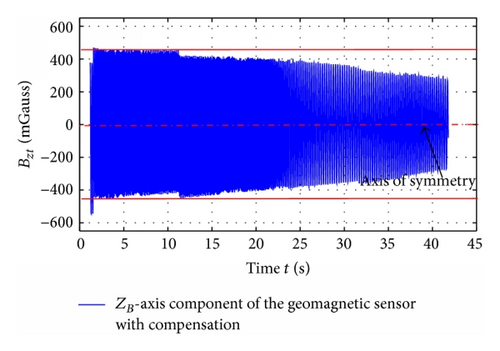
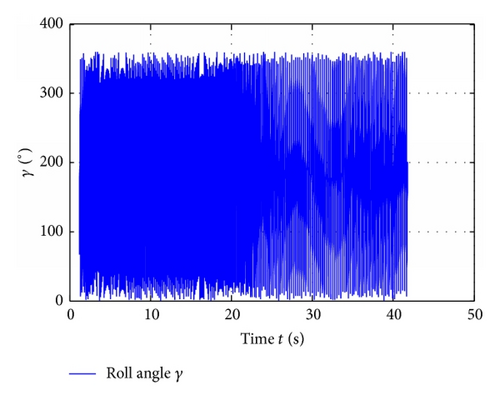
With the roll angle resolving algorithm, as mentioned above, the roll angle of the guidance kit can be worked out. The results are shown in Figure 22.

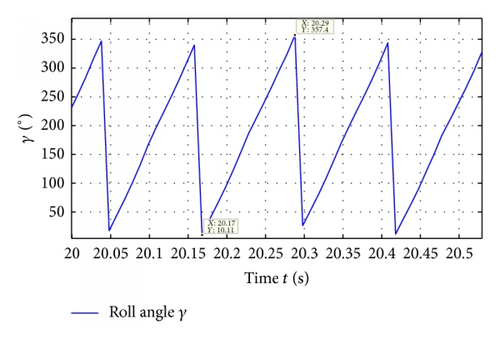
In Figure 23, the magnification of around 20 seconds is shown. It shows that the roll angle values range from 0° to 360° and vary smoothly in a good linear distribution. In that case, the roll angle resolving algorithm can work well.

5. Hardware in the Loop Simulation

In this section, hardware in the loop simulation is introduced to verify the effectiveness of the guidance law [14, 15]. And the actuator’s characteristic is considered. Here hardware in the loop simulation has two key usages: (1) testing the effectiveness of the guidance law and (2) acquiring the transform function and being introduced into the close control loop to improve the control parameters of the guidance law.

5.1. Experiment Rig

In order to simulate the motion of the mortar, a new experiment rig is designed and constructed, as shown in Figure 24. The rig takes two motors to simulate the motions of the guidance kit and the shell, and the angle testing error of the geomagnetic module is corrected by using photoelectric encoder, which is installed on the guidance kit of the rig.

5.2. Simulation Design

In the simulation experiment, simulation computer resolves the trajectory information, transforms the position and velocity to GPS signal, and then transmits the simulation GPS to projectile-borne computer. The projectile-borne computer calculates the control command signal based on the GPS and sends it to the actuator to make the canard fins act on a specific roll angle, phase angle. At the same time, the real phase angle is measured by the photoelectric encoder to analyze the following trajectory and control signal error. As the angle is passed to simulation computer to compute the following trajectory, the closed loop simulation is achieved. The whole course is made clear in Figure 25.

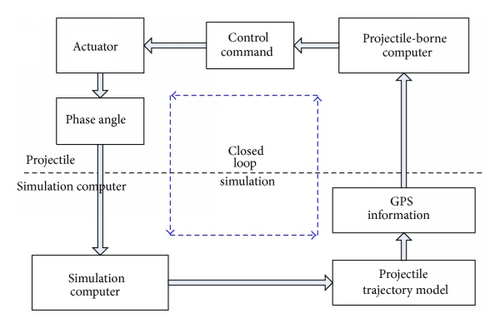
5.3. Simulation Results

To resolve the trajectory, the initial condition is given, as shown in Table 1. In the trajectory, the GPS data and roll angles are generated with noise. And the wind distribution is obtained by field measurement. The wind velocity and direction are shown in Table 2.

Table 1. Simulation condition.

Characteristics	Value
Firing angle	80°
Exit velocity	278 m/s
Wind	Table 2
GPS velocity noise	0.3 m/s
GPS position noise	10 m/s
Roll angle error	3° (random)

Table 2. Wind distribution.

Height (m)	Velocity (m/s)	Direction (°)
0	3.3	221
100	3.3	224
200	3.1	235
300	3.2	229
400	3.3	223
500	3.5	217
600	3.7	217
700	3.9	223
800	4.2	228
900	4.5	234
1000	4.9	237
1100	5.3	240
1200	5.6	243
1300	6.3	238
1400	6.9	232
1500	7.6	227
1600	8.3	228
1700	9.1	230
1800	9.9	232
1900	10.4	232
2000	10.8	231
2100	11.3	230
2200	11.4	231
2300	11.4	232
2400	11.4	232
2500	11.3	232
2600	11.3	230
2700	11.2	229
2800	11.2	227
2900	11.2	229
3000	11.3	231
3100	11.4	232
3200	11.6	232
3300	11.9	232
3400	12.2	231
3500	12.1	231
3600	11.5	233
3700	10.8	234
3800	10.1	235
3900	10.2	234
4000	10.3	233
4100	10.4	232
4200	10.4	231
4300	10.4	230
4400	10.4	230
4500	10.4	229
4600	10.4	230
4700	10.4	230
4800	10.5	231
4900	10.8	234
5000	11.2	238

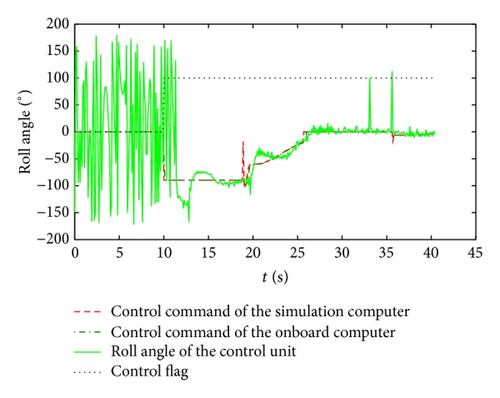
Figure 26 shows the results of the hardware in the loop simulation. Control command of the onboard computer is aligned with the command of the simulation computer, and the roll angle of the guidance kit can follow the control command well.

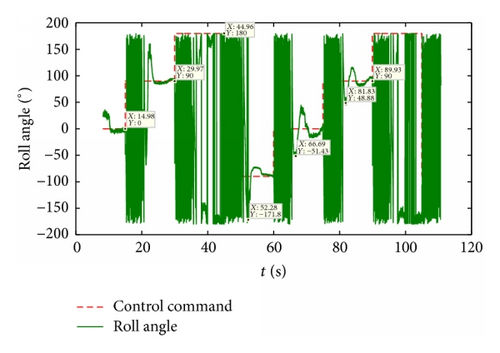
Another purpose of the experiment rig is to test the transform function. Open loop experiments were conducted to acquire the function. In the experiments, the control signal was set to 0°, 90°, 180°, and −90° for ten seconds, respectively, and between the control processions, there was a diapause lasting for 5 seconds. The experimental result is shown in Figure 27. The transform function was acquired from the data, and the function was introduced into the close control loop.

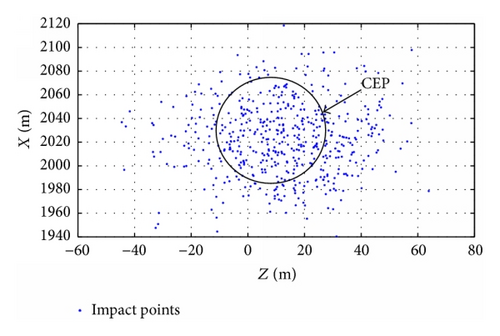
5.4. Monte Carlo Simulation

Monte Carlo method is applied to demonstrate the performance of the guidance law with GPS noise. Figures 28 and 29 show the impact point results at a range of 2.0 km for uncontrolled and controlled dispersion cases. After statistics, the guidance law makes an improvement in the Circle Error Probable (CEP)—from 46.8 m (uncontrolled) down to 2.7 m (controlled). Note that the CEP is calculated about the mean impact values for each case. The results indicate that the advanced guidance law is capable of improving the accuracy, and the effectiveness of the guidance law is verified.

6. Conclusion

This research has shown that the dual-spin mortar with fixed canard guidance kit of only GPS and geomagnetic measurements could be effectively controlled when the range is small. It is further shown that the guidance law designed is suitable and can get satisfied precision. From hardware in the loop simulation, the angle feedback of actuator action agreed well with the control command of the projectile-borne computer, from the change trend to the value. In accordance with the results of the Monte Carlo method simulation, the guidance law is verified with the high-precision and the guidance package is worked so effectively that the design is feasible for the future research.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

References

1 Bittle D. A., Hall G. A., and NourseR. W.III, Roll isolation bearing design and testing for low cost precision kill missile system, Proceedings of the AIAA Defense and Civil Space Programs Conference and Exhibit, 1998, Huntsville, Ala, USA, 52–61, AIAA-98-5418.
Google Scholar
2 Fresconi F., Cooper G., Celmins I., DeSpirito J., and Costello M., Flight mechanics of a novel guided spin-stabilized projectile concept, Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering. (2012) 226, no. 3, 327–340, https://doi.org/10.1177/0954410011408385, 2-s2.0-84858251389.
10.1177/0954410011408385
Web of Science® Google Scholar
3 Gross M., Costello M., and Fresconi F., Impact point model predictive control of a spin-stabilized projectile with instability protection, Proceedings of the AIAA Atmospheric Flight Mechanics Conference (AFM ′13), 2013, Boston, Mass, USA, American Institute of Aeronautics and Astronautics, 1–21.
Google Scholar
4 Fresconi F. and Plostins P., Control mechanism strategies for spin-stabilized projectiles, Army Research Laboratory Technical Report, 2008, no. ARL-TR-4310, Aberdeen Proving Ground, Aberdeen, Md, USA.
Google Scholar
5 Gagnon E. and Lauzon M., Course correction fuse concept analysis for in-service 155 mm spin-stabilized gunnery projectiles, Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, August 2008, Honolulu, Hawaii, USA, 1–20.
Google Scholar
6 Theodoulis S., Gassmann V., Wernert P., Dritsas L., Kitsios I., and Tzes A., Guidance and control design for a class of spin-stabilized fin-controlled projectiles, Journal of Guidance, Control, and Dynamics. (2013) 36, no. 2, 517–531, https://doi.org/10.2514/1.56520, 2-s2.0-84875713437.
10.2514/1.56520
Web of Science® Google Scholar
7 Baohua M. A., Fuse in networked technology era, Journal of Detection & Control. (2006) 28, no. 6, 1–5.
Google Scholar
8 Ollerenshaw D. and Costello M., Simplified projectile swerve solution for general control inputs, Journal of Guidance, Control, and Dynamics. (2008) 31, no. 5, 1259–1265, https://doi.org/10.2514/1.34252, 2-s2.0-53349143024.
10.2514/1.34252
Web of Science® Google Scholar
9 Barbour N. and Schmidt G., Inertial sensor technology trends, IEEE Sensors Journal. (2001) 1, no. 4, 332–339, https://doi.org/10.1109/7361.983473, 2-s2.0-0141841076.
10.1109/7361.983473
Web of Science® Google Scholar
10 Foreman D., Tournes C., and Shtessel Y., Trajectory shaping and precision guidance of a spinning mortar without angle-state feedback, Proceedings of the AIAA Guidance, Navigation, and Control Conference, August 2011, Portland, Ore, USA, American Institute of Aeronautics and Astronautics, 1–11.
Google Scholar
11 Wernert P. and Theodoulis S., Modeling and stability analysis for a class of 155 mm spin-stabilized projectiles with course correction fuse (CCF), Proceedings of the International Conference on Computational Intelligence and Software Engineering (CISE ′09), December 2009, Piscataway, NJ, USA, 1–13.
Google Scholar
12 Costello M., Modeling and simulation of a differential roll projectile, Proceedings of the AIAA Modeling and Simulation Technologies Conference, 1998, Boston, Mass, USA, 490–499.
Google Scholar
13 Costello M. and Peterson A., Linear theory of a dual-spin projectile in atmospheric flight, Journal of Guidance, Control, and Dynamics. (2000) 23, no. 5, 789–797, https://doi.org/10.2514/2.4639, 2-s2.0-0034273221.
10.2514/2.4639
Web of Science® Google Scholar
14 Ray J. A., Larson G. A., and Terry J. E., Hardware-in-the-loop support of the Longbow/HELLFIRE modular missile systems preplanned product improvement program, 4366, Technologies for Synthetic Environments: Hardware-in-the-Loop Testing VI, April 2001, Orlando, Fla, USA, 519–527, Proceedings of the SPIE, https://doi.org/10.1117/12.438102.
10.1117/12.438102
Google Scholar
15 Zhang J., Wang G., and Hao Y., The investigation of aerodynamic characteristics for two-dimensional trajectory correction projectile canard rudder device, Journal of Projectiles, Rockets, Missiles, and Guidance. (2013) 33, no. 2, 88–91.
Google Scholar

Citing Literature

All articles

Guidance Law Design for a Class of Dual-Spin Mortars

Abstract

1. Introduction

2. Guidance Package and Problem Formulation