Dispersion Features of Conducting Sheath Helix Embedded Elliptical and Circular Fibers with Chiral Nihility Core
Abstract
Discussions have been made of the electromagnetic wave propagation through optical fibers of elliptical and circular cross-sections with the loadings of conducting sheath helix at the core-clad interface with particular orientations. In both geometrical situations, the core section of fiber is assumed to be composed of chiral nihility medium, and the clad remains linear, homogeneous, isotropic, and nonmagnetic dielectric. Dispersion relations are deduced for both fiber structures, followed by the analysis of dispersion features considering a few low-order EH modes. Furthermore, the effects of conducting helix pitch angle on the features of wave propagation are also discussed.
1. Introduction
Chiral materials possess a unique feature of exhibiting optical activity. Linearly polarized light upon passing through such materials splits into two circularly polarized light waves, and the medium behaves as isotropic for these [1]. Such complex mediums with different structural designs have been studied extensively.
In chiral nihility mediums, there exist two (right- and left-) circularly polarized eigenwaves such that E = E+ + E− and H± = ±(j/η1)(E±) with wavenumbers as k± = ±κk0 (a positive sign being the indication of right-circular and a negative sign for left-circular polarization). Also, η1 is the medium impedance, given by . The two circularly polarized waves propagating through chiral nihility mediums contribute to backward waves. Apart from this, nihility mediums also exhibit the phenomenon of negative refraction/reflection.
Materials with such exotic features have drawn attention of many researchers as these offer potential applications in optics. Within the context, several alternate efforts have been made for the development of such materials [5, 6]; references [7, 8] discuss the electromagnetic behavior of these.
Optical fibers embedded with conducting sheath helix structures at the core-clad interface allow altering the dispersion characteristics of these through properly adjusting the helix pitch angle [9–13]. Such helical structures have been in use in travelling wave tubes for the purpose of microwave amplification [14]. References [15, 16] report the dispersion behavior of helical clad elliptic fibers. It is noteworthy that elliptical waveguide has the distinct advantage that the transmission modes are more stable in these, and the attenuation modes are reduced as compared with its circular counterpart. In such guides, only hybrid modes exist to satisfy the boundary conditions [17].
The investigation of modified fiber structures with embedded conducting helix and nihility mediums would be interesting. As stated above, chiral nihility mediums have been greatly discussed in the literature [2]. As the nihility mediums have simultaneously vanishing values of permittivity and permeability, the motivation of the present paper comes from the idea of incorporating such medium into elliptical and cylindrical fiber geometries. It is well known that elliptical fibers have been of great use in signal detection in communication systems. However, in the present study, the emphasis has been given more on the dispersion properties that can be tailored through the incorporation of conducting sheath helical windings.
Iqbal et al. [18] reported before the dispersion features of helical clad fibers with chiral nihility mediums. The present communication remains a platform where we present a comparative study of fibers with elliptical and circular cross-sections in which chiral nihility cylinders are encapsulated with infinitely extended dielectric clads in the transverse direction. We emphasize on the determination of effective refractive index (RI) as a function of normalized frequency for the fiber structures under consideration. The radial Mathieu function and its modified forms are incorporated for the determination of electric/magnetic fields in elliptical case [19], and the investigations are made corresponding to a few low-order hybrid modes under the situation of two extreme values of helix pitch angle.
2. Formulation
In the present analysis, we consider elliptical and circular fiber geometries with the loadings of conducting sheath helical windings with certain orientations at the core-clad interface. For instance, we consider the two extreme situations when the orientation becomes perpendicular and parallel to the optical axis. Furthermore, for both the fiber structures, the core section is composed of chiral nihility medium, and the clad region is linear, homogeneous, and isotropic dielectric medium. We now discuss the two fiber structures individually.
2.1. The Case of Elliptical Fiber
Figure 1(a) shows fiber structure of elliptical cross-section with the core of chiral nihility medium and dielectric clad. The structural geometry essentially approves the use of orthogonal elliptical coordinates (ξ, η, z), as shown in Figure 1(b). Here, ξ represents contour surfaces of confocal elliptical cylinder and takes the value 0 ≤ ξ ≤ +∞, while η represents confocal hyperbolic cylinders having range 0 ≤ ξ ≤ 2π. The core-clad boundary exists at constant confocal elliptic cylinder ξ = ξ0. The distance between the two foci is 2q = 2ae, where e is the eccentricity of elliptical cross-section, determined as 1/cosh(ξ0), and a is the semimajor axis of length qcosh(ξ0) along the x-direction. Also, the semiminor axis along y-axis has the length b = qsinh(ξ0). Both the core and the clad regions are assumed to be nonmagnetic in nature; that is, μ1 = μ2 = μ0 (permeability of free-space).
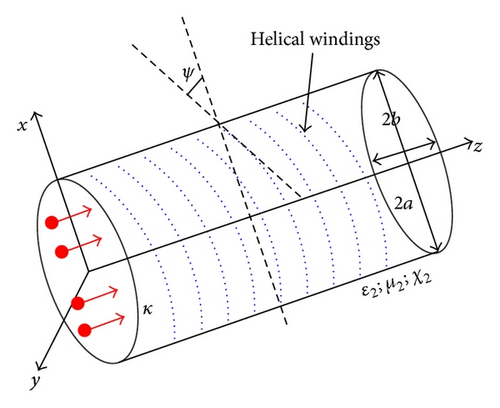

2.2. The Case of Circular Fiber
3. Results and Discussion
We now focus on the dispersion characteristics of fiber structures, which are greatly governed by the pitch angle of helical windings. For computations, we choose two extreme values of pitch angle as 0° and 90°. The other fiber parameters are the core chirality parameter κ as 1.55 and 1.46, the clad RI n2 as 1.49 (acrylic glass) and 1.444 (silica), the operating wavelength λ as 1.55 μm, semimajor (a) and semiminor (b) axes lengths as 10 μm and 7.6 μm (in the elliptical case), respectively (for circular geometry the parameter a is assumed to be the radius of circular cross-section), and the impedance of chiral nihility medium (in the core section) as equal to that of free-space. Under the scenario of hybrid EH mode excitation, computations are made for the values of mode index m as 0, 1, and 2.
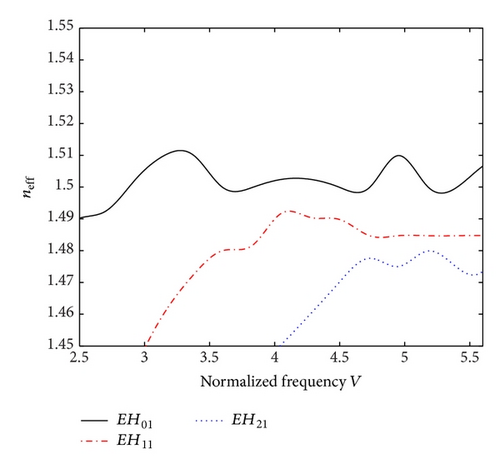
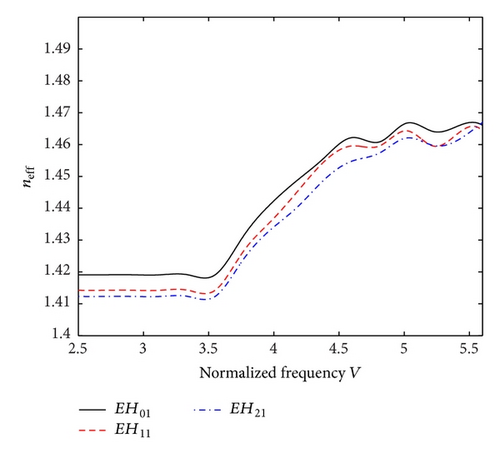
Figures 2 and 3 and Figures 4 and 5, respectively, correspond to the situations of elliptical and circular core fibers, wherein the effective RI (neff) is plotted against the normalized frequency parameter V. Considering the three low-order hybrid modes EH01, EH11, and EH21, plots are made for 0° and 90° helix pitch angles along with the consideration of the core chirality parameter κ as 1.55 and 1.46, and the clad RI n2 as 1.49 and 1.444. Within the context, it remains noteworthy that the behavior of chiral nihility mediums is frequency dependent.
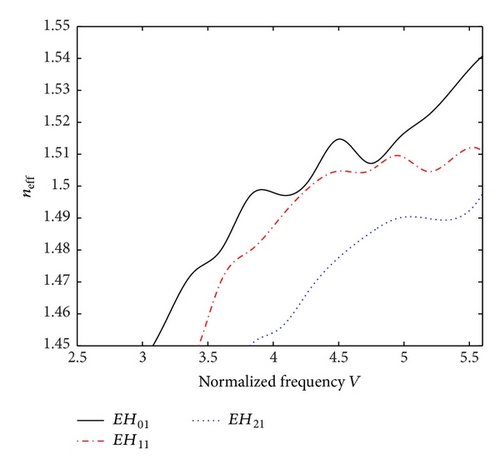
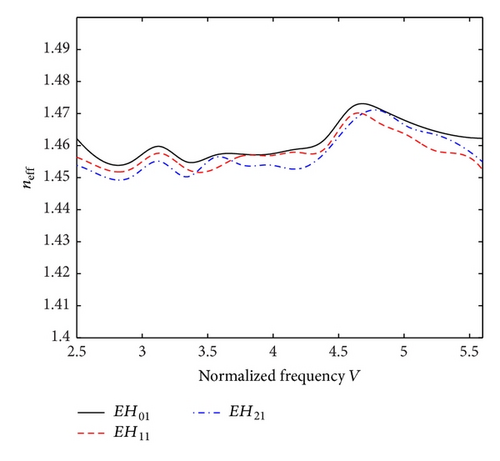
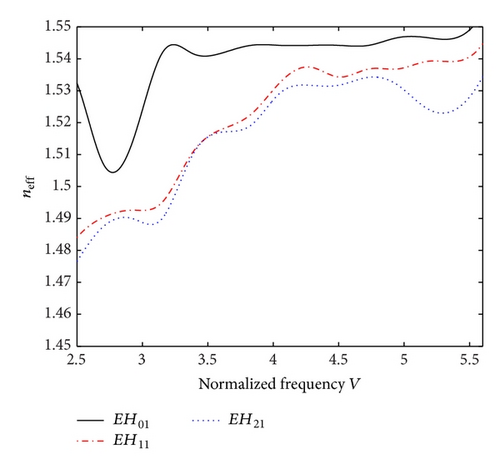
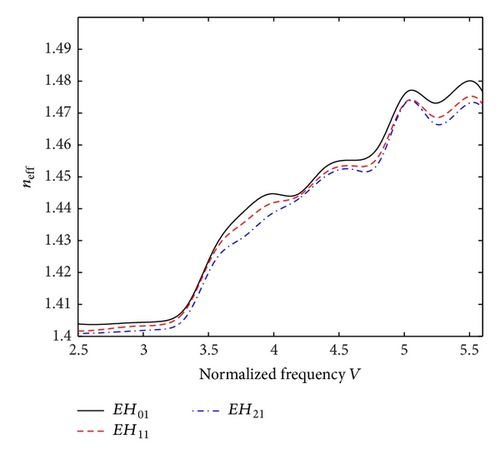
Figures 2(a) and 2(b), respectively, illustrate the dispersion characteristics of elliptical fiber having the characteristic helix pitch angles as 0° and 90° under the consideration of the three low-order hybrid modes EH01, EH11, and EH21. We find that, in both the situations, the values of neff generally decrease with the increase in mode order. We observe from Figure 2(a) that, under the situation when the conducting helical windings are perpendicular to the direction of wave propagation, the EH01, EH11, and EH21 modes exhibit approximate cutoff values at V ≤ 3.726, V ≤ 4.052, and V ≤ 4.99, respectively. As such, the lowest EH01 mode shows the least cutoff. After the cutoff V-values, the neff for all the modes gradually increase with the increase in V. Furthermore, the peaks and dips observed in the neff-V plots corresponding to every mode demonstrate, respectively, the presence of slow- and fast-waves in the fiber structure. In this respect, the EH01 mode contributes more strongly to the slow- and fast-waves in the vicinity of V≅3.8 and V≅4.4.
The case of parallel orientation (i.e., ψ = 90°) of conducting helix is shown in Figure 2(b), wherein we observe that the EH01 mode does not exhibit any cutoff within the specified frequency range (V = 1.547, as obtained by the use of [17]). For the next EH11 and EH21 modes, the cutoff V-values exist at V = 4.004 and V = 6.451, respectively. As such, we find that a change in conducting helix orientation causes altering the dispersion behavior, and particularly, the longitudinal orientation of helix structure has the tendency to reduce the modal cutoffs, except for the mode EH21 for which the cutoff is increased. We also notice that the EH01 mode contributes more strongly to the slow- and fast-waves near V≅3.2 and V≅4.9 than the other two higher modes.
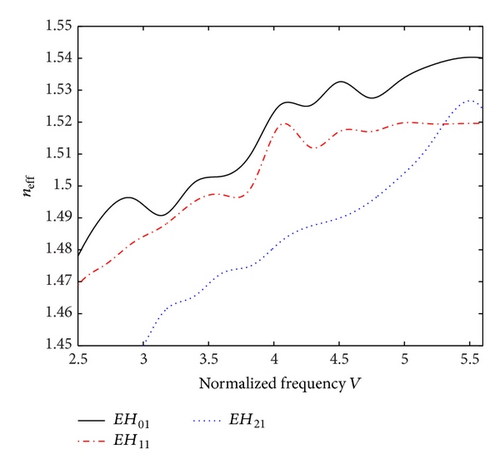
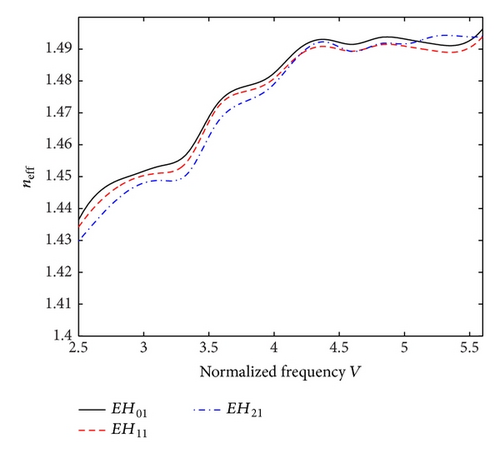
Considering κ = 1.46 and n2 = 1.444, and keeping the other operating conditions as the same, the results are illustrated in Figures 3(a) and 3(b). We observe that, for a 0° helix pitch, the cutoff frequency increases for the EH01 mode (V = 2.599), and it is decreased corresponding to the other higher order modes under consideration. It can be noticed that the cutoff frequencies occur at V = 2.665 and V = 2.819 corresponding to the EH11 and the EH21 modes, respectively. Furthermore, the surface modes occur at the normalized frequencies V > 4.5, V > 4.831, and V > 4.925 corresponding to the EH01, EH11, and EH21 modes, respectively. On the other hand, for a 90° helix pitch angle, the cutoff frequency increases corresponding to the EH21 mode only, and it gets decreased for the other modes at this value of pitch. Apart from these, the results demonstrate that a 90° helix pitch makes the surface modes to occur at lower frequencies than what have been observed corresponding to a 0° pitch.
Figures 4(a) and 4(b) correspond to the dispersion situations of fiber with circular cross-section when the conducting helix pitch angles assume the values 0° and 90°, respectively. Similarly to the case of elliptical fiber (as discussed above), we consider the three low-order hybrid modes EH01, EH11, and EH21, and we find that, in this case as well, the values of neff generally increase with the decrease in mode order. We observe from Figure 4(a) that, when the helical windings are oriented in the direction perpendicular to the direction of propagation, all the stated modes exhibit cutoffs at V ≤ 1.956, V ≤ 2.672, and V ≤ 3.153. Furthermore, corresponding to the EH01 mode, a strong dip in the neff-V plot near V≅2.75 exhibits the presence of slow- and fast-waves in the fiber. The other higher modes also contribute to such situations, but those are not as strong as that reflected by the EH01 mode.
Increasing the helix pitch angle to 90°, dispersion plots corresponding to all the low-order hybrid modes are shown in Figure 4(b). We observe from this figure that cutoff frequencies of EH01, EH11, and EH21 modes occur at V ≤ 2.677, V ≤ 3.226, and V ≤ 4.512, respectively. Furthermore, the conditions of slow- and fast-waves are better observed for the EH01 and EH11 modes for certain values of V. Comparing the dispersion behavior of circular fiber with that of the elliptical fiber, we notice that the average value of neff remains a little larger in the case of the former one, and the highest value of neff is attained when the helical windings are oriented perpendicular to the direction of wave propagation. Apart from this, the condition very close to mode degeneracy is observed for such helical orientation in fiber with circular cross-section, which is not found in the case of elliptical fiber.
Taking into account κ = 1.46 and n2 = 1.444, the obtained results are shown in Figures 5(a) and 5(b). We notice that, corresponding to a 0° angle of helix pitch, the cutoff frequency is increased for the EH01 and the EH11 modes, and it is decreased for the EH21 mode. Increasing the pitch to 90°, the cutoff frequency is decreased for all the stated modes. Furthermore, the effect due to the alteration of pitch angle on the surface modes can also be observed from Figures 5(a) and 5(b) (i.e., corresponding to 0° pitch angle, V > 3.389 ( EH01), V > 3.417 ( EH11), and V > 3.471 ( EH21), and corresponding to 90° pitch, V > 4.817 ( EH01), V > 4.874 ( EH11), and V > 4.875 ( EH21)).
In the foregoing investigation, results are obtained for different values of chirality parameter in the fiber core and the RI values of the fiber clad taking into account the cases of circular and elliptical fibers. From the respective plots, we can analyze the cutoffs for the guided and surface modes. In [20], cutoff and surface modes for the EH01 mode occur at the normalized frequencies V = 2.405 and V = 1.332, respectively. In the present investigation, however, corresponding to the chirality parameter in core κ = 1.55 and the RI value of clad n2 = 1.49, cutoffs occur at V = 1.956 (for the pitch angle 0°) and V = 2.677 (for the pitch angle 90°), and these cutoff frequencies show increase to V = 2.599 (for the pitch angle 0°) and V = 3.841 (for the pitch angle 90°) with the variation in system parameters (i.e., the core chirality κ = 1.46 and the clad RI of clad n2 = 1.444). No surface mode has been found to exist in the case of parametric values κ = 1.55 and n2 = 1.49; these occur corresponding to the situation of choosing κ = 1.46, n2 = 1.444 instead. For the other two modes (EH11 and EH−11) in [20], cutoff frequencies are reported to occur at V = 0 (for the EH11 mode) and V = 3.832 (for the EH−11 mode), whereas no surface modes exist. However, in present analysis, cutoff frequencies (corresponding to the cases of κ = 1.55, 1.46, n2 = 1.49, 1.444) and surface modes (corresponding to κ = 1.46, n2 = 1.444) are investigated for these modes (EH11 and EH21), as described earlier.
4. Conclusion
The aforesaid discussion is pivoted to the role of conducting sheath helix embedded in chiral nihility fibers with circular and elliptical cross-sections. Considering the three low-order hybrid modes, analyses are made of the dispersion characteristics under the circumstances when the helical windings assume orientations perpendicular as well as parallel to the direction of wave propagation. It has been found that the helix orientations greatly affect the cutoff characteristics of modes. In certain situations, modes in circular fiber do not exhibit any cutoff, and also, the perpendicular orientation of conducting sheath helix in these brings in the condition close to mode degeneracy—the situation not observed for elliptical fibers. It is also found that the modal cutoff values for elliptical fiber are generally higher than those observed for circular fiber. Dispersion characteristics clearly indicate the existence of slow- and fast-waves in the fiber structure depending on the structural geometry as well as the helix orientations.
Conflict of Interests
The authors declare that there is no conflict of interests regarding the publication of this paper.
Acknowledgments
The authors are thankful to the two anonymous reviewers for making constructive criticisms on the paper. Also, they gratefully acknowledge the Ministry of Higher Education (Malaysia) for providing financial support to the work.




