A Modularized Noise Analysis Method with Its Application in Readout Circuit Design

1. Introduction

An infrared detector has a wide range of applications in areas of military, research, and manufacture, whose core part is an infrared focal plane assembly [1, 2]. The assembly mainly consists of two parts, a focal plane array (FPA) that functions to convert radiation to current signal and a readout integrated circuit (ROIC) that is responsible for realization of serial processing of signals sampled from the FPA [3].

As an essential part of the signal chain, the research on integrators and correlated double sampler (CDS) has been highlighted since they were invented, alongside with the character of noise transferring from end to end, which is affected by various factors like amplifying, sampling, filtering, and so on. An integrator conducts current signals through an integration capacitor to be transformed into voltages, which inevitably induces strong reset noise. So a CDS has to be used to suppress it, which also subtracts the reference voltage from the output to present a net integration voltage. Applications of FPAs with large format and high resolution put forward more harsh demands on the small layout area. In order to give an optimization for noise performance of a ROIC, a modularized noise analysis method is proposed for a readout cell, consisting of an integrator and a new type of correlated double sampler (CDS), both of which are switched capacitor circuits, where all the MOSFETs are optimized in subthreshold region to be acceptable to the power limitation of large format FPAs [4, 5]. The modularized noise analysis begins with the architecture of the readout cell that is for pixel level ROICs, operating in snapshot mode. Afterwards the noise model is built using transfer functions and the method of presenting the transfer process of noise in the form of matrix is given, through which we can describe the contribution of each noise source to the whole output noise distinctly. In the end, calculations of noise for the proposed readout cell are carried out by the transfer function method and transient simulations utilizing Verilog-A, respectively. The results due to the two methods show good agreement.

2. Architecture of the ROIC

Figure 1 depicts the architecture of the ROIC, whose readout timing operates on pixel level. Snapshot mode is employed. Each pixel corresponds to each readout unit cell, which are connected electrically through indium bump [6]. All the pixels are exposed to radiation simultaneously and transfer the generated photocurrent to the corresponding readout unit cells. Utilizing the architecture provides the capability of expanding integration time, which can adapt to the situation of low intensity radiation [7]. After an integration period ends, with the control of digital logical signals, the integration voltage maintained in each readout unit cell is transmitted serially through a multiplexer and then delivered outside the ROIC through a buffer.

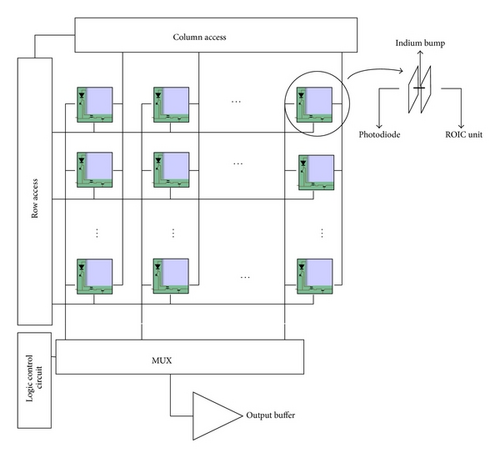
3. Design of the Readout Unit Cell

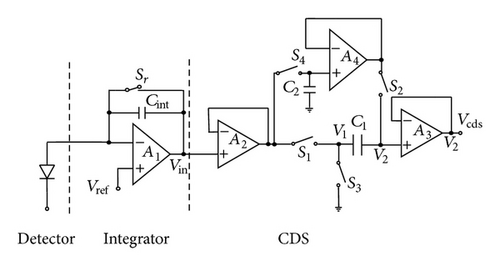
The structure of the proposed readout unit cell is shown in Figure 2, constituted by two parts, an integrator and a CDS. The integrator adopts the CTIA structure, which provides nearly 100% injection efficiency and linearity. Meanwhile the CDS is composed of three OPs, A₂, A₃, and A₄, connected as buffers, two sampling capacitors, and four complementary switches, S₁, S₂, S₃, and S₄. From those A₂ and A₃ act to isolate switching operations between the former and latter circuit part.

Herein the structure we proposed is compared with four different ROIC unit cells in [8–11]. The added CDS part provides the capability of suppressing low frequency noise from reset operation and photocurrent for the proposed ROIC one which in aspect of noise performance surpasses those referred to in [8–10] without CDS circuits. The linearity of the BDI structure in [11] can reach 99% which is high enough for the type of structure while for the CTIA type like the one we proposed and these in [8–10] it is easy to achieve more than 99.5% linearity; besides, the power dissipation of the two types makes no difference if the static power of the OP involved is the same. Thus how to choose the most suitable OP and optimize the power dissipation of the OPs involved is another crucial problem.

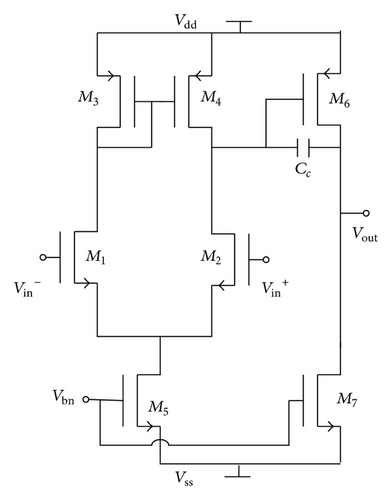
Several types of structure of OP are able to be used for the proposed unit cell, such as cascade OP, folded cascade OP, two-stage OP, and gain boost OP. Table 1 gives the comparison among them [12]. From Table 1 we see that, except for the speed disadvantage, the two-stage OP is the best choice, as shown in Figure 3, which just maintains medium power obtaining high gain which can guarantee low static error. On account of the application of the proposed ROIC unit for infrared image acquisition, the clock operations are not in a high frequency, so the speed of the OPs is easy to achieve in either of the OP types.

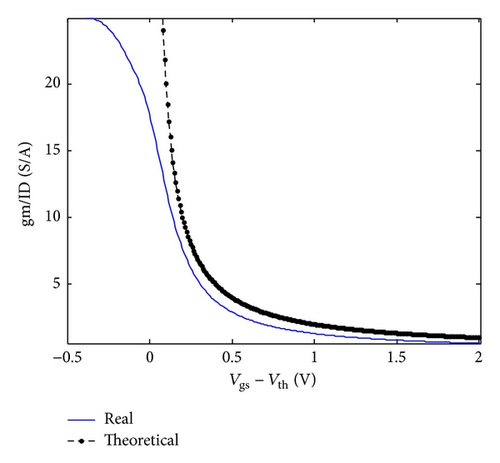
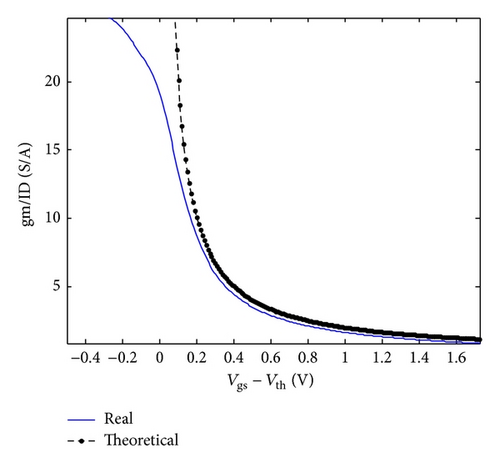
It is worth noting that the behavioural model of MOSFETs in subthreshold region is not accurate enough when the process of ICs goes into deep submicron, like 0.18 μm. To do the calculation precisely, all the parameters adopted should be those obtained through simulations. Figure 4 shows the qualitative illustration of the real gm-to-channel current ratio compared with the theoretical one, (a) for NMOS and (b) for PMOS, from which it can be seen that although the ratio does not increase as fast as the theoretical curve expects when the V_gs − V_th goes down, it is much larger in the subthreshold region than that in the saturation region. That is what we desire to improve efficiency of utilizing current.

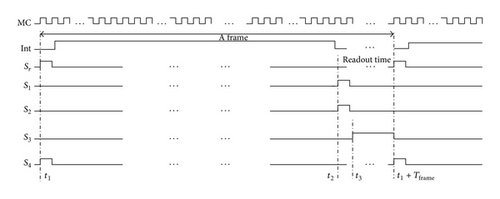
The output node “V_cds” should be equal to “V₂” under ideal condition, thus giving the net integration voltage and subtracting the charge injection error brought by the reset process of integrator. However the transmission of signal will be influenced by noise, which is analyzed in the next section in detail.

The transient response of the readout unit cell is depicted in Figure 6. We can see that the reset voltage equal to the reference voltage is 2.5 V and the “V_in” node becomes 1.5 V from 2.5 V through integration. At “t₃” S₃ turns on, the “V₁” node connects to ground, and “V₂” sets to 1 V, which drives the output voltage to 1 V, the net integration voltage. Besides, the static power dissipation of the proposed readout unit cell reaches 2.8 μW with 700 nW per OP.

4. Noise Model Based on Transfer Function

4.1. The Integrator Part

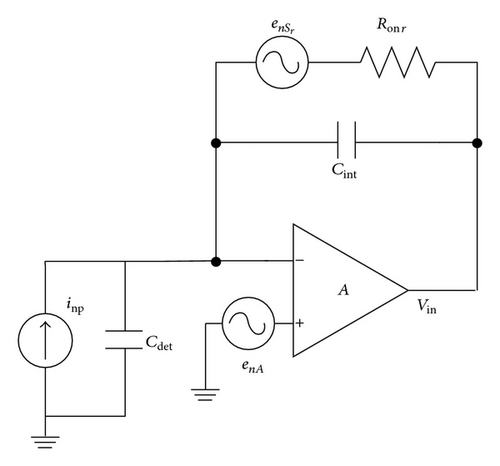
The noise model of the integrator part is shown in Figure 7. There are three noise sources: photocurrent noise caused by photoelectric effect which cannot be avoided [14], the noise caused by the reset process of switch S_r, and the noise of the OP presenting as the input reference noise source.

For CTIA ROIC, photocurrent and its noise integrate on C_int directly, which can be expressed as

$$ ()

where T represents the time length of a frame and (3) can be comprehended as i(t) convolving a window function with T_int window length [15]. So in frequency domain the process can be expressed as

$$ ()

where H_i(f) is the transfer function of photocurrent noise source to the “V_in” node and the contribution to the output noise of the integrator part is given in the form of power spectrum density (PSD) by

$$ ()

where $$ represents the PSD of noise voltage on “V_in” node induced by $$, that is, the PSD of photocurrent noise from the corresponding pixel. The transfer function of the OP noise source enA, denoted by H_A(f), can be derived by the model depicted in Figure 8:

$$ ()

where C_det is the shunt capacitor of the pixel and A(f) is the open loop transfer function of the OP, which can be expressed as [11]

$$ ()

where A₀ and GBW are the low frequency gain and gain bandwidth product of the OP.

We can get the transfer function of enSr by the same approach, which is given by

$$ ()

where R_off is the off-resistance of the switch S_r. The output noise of integrator part can be expressed in matrix, which is given by

$$ ()

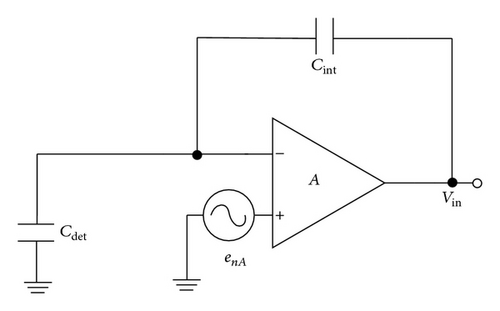
4.2. CDS Part

The noise model of the CDS is shown in Figure 9, where all the OPs are connected as unity-gain buffers. Because of the noninverting structure, their output resistance is reduced by A₀ times which can be ignored based on the Thevenin equivalent.

When the integrator resets, the voltage on “V_in” node is sampled on C₂; after the integration, the voltage on “V_in” node is transferred to the “V₁” node at the moment S₁ and S₂ turn on. The voltage across C₁ is

$$ ()

For Δ time after S₁ and S₂ turn off and S₃ turns on, the voltage on “V₂” is

$$ ()

The expression in frequency domain is given by

$$ ()

where $$, $$, and $$ stand for the PSD of noise voltage on “V₂,” across C₁ at “nT” and on “V₁” at “n(T + Δ).” So the latter two can be expressed as follows:

$$ ()

$$ ()

where H_X(f) is the transfer function of the noise source X to the nodes across C₁, respectively. e_nint is the noise of “V_in” node at the moment an integration ends which is equal to $$. H_D(f) = exp(−jωT_int) represents the reset process that is before the integration starts [15]. Consider

$$ ()

n(T + Δ) marks the end of one period of correlated double sampling; at that time the noise on “V₂” and the noise of A₃ are transferred through A₃ with a transfer function denoted by A_UG(f) to the “V_cds” node:

$$ ()

$$ ()

The PSD of the noise of the output node “V_cds” of CDS can be written as the following equation:

$$ ()

where H₂ is a diagonal matrix whose diagonal line corresponds to the transfer functions of each noise element in E_cds. It can be seen that the first three elements in E_cds are noise sources from the integrator. To show the noise sources in CDS, we define

$$ ()

So the following expression can be acquired:

$$ ()

where T converts O₁ to an enhanced length with 0, which means O₁ changes from $$ to $$. Written briefly, the transmission of noise through the two parts of the readout unit cell is

$$ ()

Every noise source in each part of the readout unit cell transmitting to the output node is expressed precisely and compactly by using (22). The design contains only two parts, so the numbers marking the parts are 1 and 2. Under the situation of much more constituent parts, the transmission of noise source can be written as

$$ ()

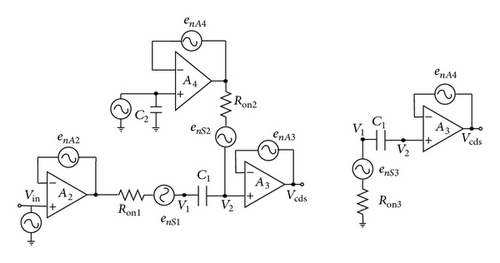
5. Noise Computing

5.1. Noise Computing Based on Transfer Function

The photocurrent noise is related to the value of the generating photocurrent, which varies with the radiation intensity. Strictly speaking, it is pixel noise, which does not belong to the noise of readout circuits [15]. Thus the photocurrent noise will not be calculated in the paper. All the noise sources in the readout unit cell are induced by the MOSFETs. For the switches, MOSFETs operating in linear region produce thermal noise modeled by [12, 16]

$$ ()

where k is the Boltzman constant, T is the absolute temperature, and R_oni represents the on-resistance of the switches. MOSFETs in the OP operate in the subthreshold region, producing thermal noise and 1/f noise; the whole noise of an OP can be represented as the reference input noise:

$$ ()

where K_1e and K_2e represent thermal noise factor and 1/f noise factor for the OPs, respectively. The detail of computing expression can be referred to in the chapter introducing OP of [12, 16], through which the specific values of the two parameter are obtained. The process on which the project is based is Globalfoundries 0.18 μm Industry Compatible Dual Voltage 1.8 V/3.3 V Process. The frequency character of the OP is simulated, which is shown in Figure 10. From it we can see that the OP achieve a 61-degree phase margin that leads to stability when countering an input of a step signal.

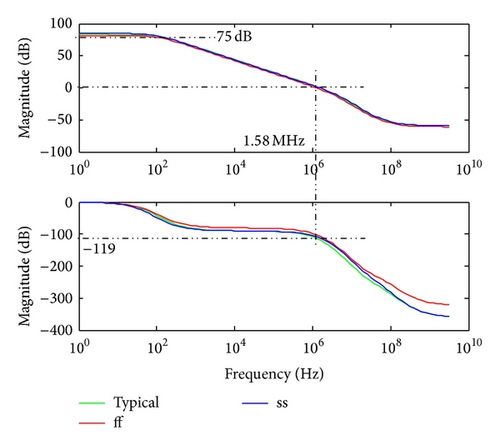
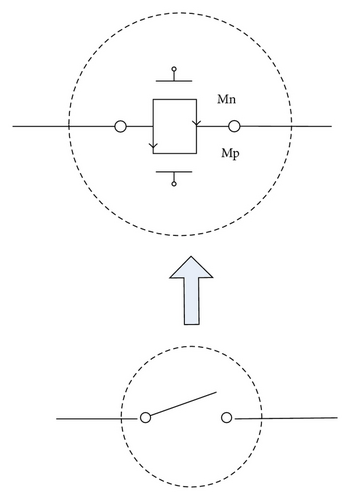
The switches in the proposed ROIC are implemented as CMOS switches, individual of which consists of a P type MOSFET, Mp, and an N type MOSFET, Mn, as shown in Figure 11. The W/L of both of the two MOSFETs are set to be 0.3 μm/2.35 μm. The simulation curve of resistance of the CMOS switch is shown in Figure 12, where the input signal spans from 0.5 V to 2.5 V. Figures 12(a) and 12(b) present the value of maximum on-resistance 2.2 kΩ and the value of minimum off-resistance 1 GΩ.

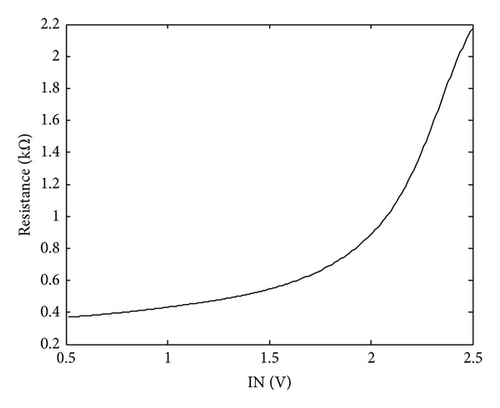
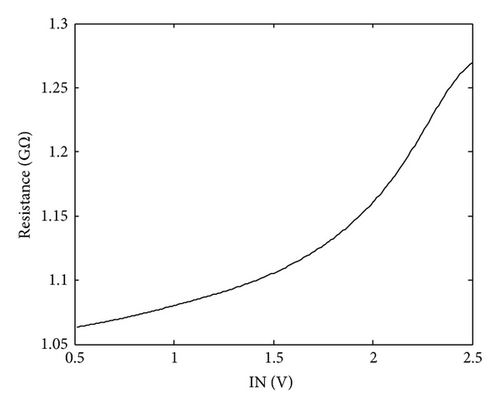
The parameters used for the calculation of noise are summarized in Table 2, where we assume that all the OPs have the same parameters and so do the switches.

Table 2. Parameters of noise calculation.

Ron (on-resistance of switch)	2.2 kΩ
Roff (off-resistance of switch)	1 GΩ
K1e (thermal noise parameter of OP)	4 × 10−17 V2/Hz
K2e (1/f noise parameter of OP)	4 × 10−12 V2/Hz
GBW (gain bandwidth product of OP)	1.58 MHz
A0 (low frequency gain of OP)	75 dB

For the application of high resolution, the area of a single pixel is restricted, leading to the limited layout area for the readout unit cell. With respect to the fact that capacitors consume the largest area resource, therefore, with the guarantee of sufficient layout area for the MOSFETs, more layout areas should be distributed to the three capacitors in the unit cell. Through calculations, effect on the output noise due to C₂ can be neglected, which should be designed small to save up layout area to allow larger C_int and C₁. With the limitation of 30 μm × 30 μm layout area, the maximum of the sum of the two capacitors is 2 pF.

The contribution of each noise source to the output noise is calculated using the transfer functions in Section 3, which is shown in Figure 13, where T_int is set as 100 μs. Figure 13(a) depicts the dependence of the output noise, integrator noise, and CDS noise on the C_int. The diagram reveals an opposite variation trend. The integrator noise is an increasing function and the CDS noise is a decreasing function, which results from the limitation of the sum of capacitors. C_int increase leads to C₁ decrease inevitably, causing enlargement of the bandwidth of transfer functions of noise sources in CDS, which weakens the ability of low pass filtering. Figure 13(b) gives the curves of thermal noise, 1/f noise, and reset noise with the change of C_int. We can see that 1/f noise and reset noise increase with C_int increase while an optimal point appears for the thermal noise which is the majority, at 0.66 pF. When the C_int is smaller than 0.26 pF, the reset noise is smaller than 1/f noise. The output noise reaches the minimum at 74.1 μV when the C_int is 0.74 pF and C₁ is 1.26 pF.

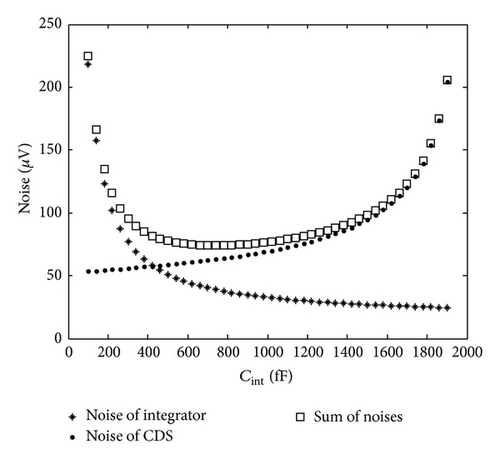
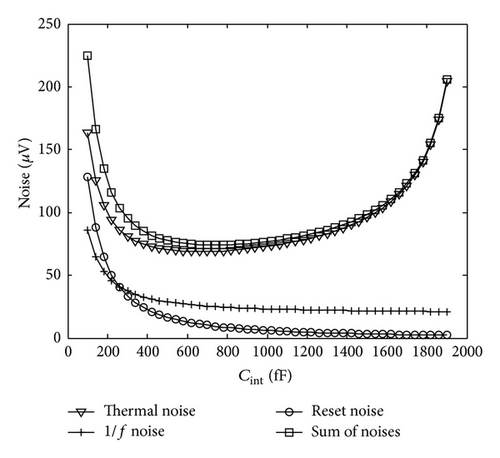
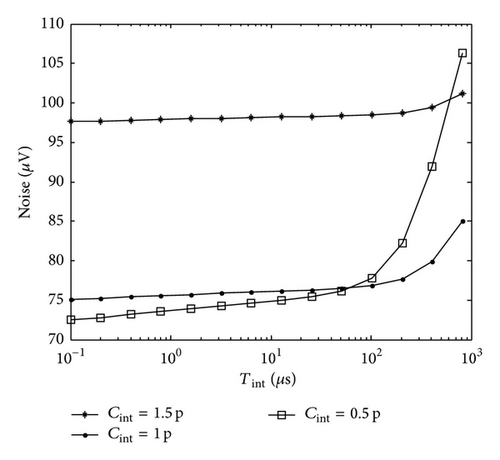
Figure 14 shows the output noise as a function of T_int with three different C_int. It can be seen that the output noise increases when T_int increases, despite different C_int. This is mainly because the increasing of T_int results in increasing of interval of correlated double sampling, which weakens the capability of suppressing 1/f noise and reset noise. From the figure we also get that, with smaller C_int, the increase speed of output noise is faster.

6. Conclusion

To adapt the application of imaging for large format and high resolution, a new readout cell with low power and small layout area is proposed, consisting of an integrator and a new type of CDS, both of which are switched capacitor circuits where all the MOSFETs are optimized in subthreshold region. The integrator adopts CTIA structure and the CDS is comprised of four switches, three Ops, and two capacitors. The noise model is built using transfer function in Section 3 and a method of presenting the transfer process of noise in the form of matrix is given, through which we can describe the contribution of each noise source to the whole output noise distinctly. In Section 4, noise analysis of the proposed readout cell is carried out by the transfer function method and transient analysis utilizing Verilog-A, respectively. The results showing good agreement verify the feasibility of the method presented through matrix. Under the limitation of layout area less than 30 μm × 30 μm, the integrator noise is an increasing function of C_int and the CDS noise is a decreasing function. With respect to the types of noise, 1/f noise and reset noise increase with C_int increase while an optimal point appears for the thermal noise which is the majority. The integration capacitor should be selected as 0.74 pF to achieve an optimal noise performance, the whole output noise reaching the minimum value at 74.1 μV.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.