By three independent hints it will be demonstrated that still at present there is a substantial lack of theoretical understanding of the CMB phenomenon. One point, as we show, is that at the phase of the recombination era one cannot assume complete thermodynamic equilibrium conditions but has to face both deviations in the velocity distributions of leptons and baryons from a Maxwell-Boltzmann distribution and automatically correlated deviations of photons from a Planck law. Another point is that at the conventional understanding of the CMB evolution in an expanding universe one has to face growing CMB temperatures with growing look-back times. We show, however, here that the expected CMB temperature increases would be prohibitive to star formation in galaxies at redshifts higher than z = 2 where nevertheless the cosmologically most relevant supernovae have been observed. The third point in our present study has to do with the assumption of a constant vacuum energy density which is required by the present ΛCDM-cosmology. Our studies here rather lead to the conclusion that cosmic vacuum energy density scales with the inverse square of the cosmic expansion scale R = R(t). Thus we come to the conclusion that with the interpretation of the present-day high quality CMB data still needs to be considered carefully.

1. Introduction

The cosmic background radiation (CMB) has been continuously full-sky monitored since 1989 beginning with COBE, continued by WMAP [1] and now recently by PLANCK [2]. Though with these series of successful and continuous measurements our knowledge of the structure of the CMB has tremendously grown, representing nowadays this cosmologically highly relevant phenomenon in an enormous quality of spectral and spatial resolution; these data, however good in quality, do not speak for themselves. They rather need to be interpreted on the basis of a theoretical context understanding of the CMB origin. The latter, however, has not grown in quality as CMB data have. This paper wants to show some aspects of modern cosmological research in new lights. Thereby it may also serve readers with some hesitation towards present-day cosmology and give them some encouragement. One needs to be convinced that a scientific discipline like cosmology is built on safe conceptual and physical grounds, before one can appreciate the most recent messages from modern precision cosmology. One only can appreciate cosmological numbers like a Hubble constant of H₀ = 73 km/s/Mpc and an age of the universe of τ₀ = 13.7 GYr [1] as eminent findings of the present epoch, when one accepts a universe that presently expands in an accelerated form due to being driven by vacuum pressure. This puts the question what are the basic prerequisites of modern cosmology?

At first it is the assumption that all relevant facts determining the global structures of the universe and their internal dynamics have been found at present times. This puts the question what part of the world may presently be screened out by our world horizon, which nevertheless influences the cosmological reality inside? If, as generally believed, the cosmic microwave background (CMB) sky is such a horizon, then everything deeper in the cosmological past must be invented as a cosmologic ingredient that never becomes an observational fact. On the other hand, when inside that horizon only something not of global but of local relevance is seen, then the extrapolation from what is seen to the whole universe is scientifically questionable.

In this paper we start out from a critical look on the properties of cosmic microwave background (CMB) radiation, the oldest picture of the universe, and investigate basic assumptions made when taking this background as the almanac of basic cosmological facts. Neither the exact initial thermodynamical equilibrium state of this CMB radiation is guaranteed, nor its behaviour during the epochs of cosmic expansion is predictable without strong assumptions on an unperturbed homologous expansion of the universe. The claim connected with this assumption that the CMB radiation must have been much hotter in the past may even bring cosmologists in unexpected explanatory needs to explain star formation in the early universe as will be shown.

2. Does Planck Stay Planck, If It Ever Was?

2.1. The Cosmic Microwave Background Tested by Cosmic Thermometers

It is generally well known that we are surrounded by the so-called cosmic microwave background (CMB) radiation. This highly homogeneous and isotropic black-body radiation [1, 5–7] is understood as relict of the early cosmic recombination era when due to removal of electrically charged particles by electron-proton recombinations the universe for the times furtheron became transparent for photons. Since that time cosmic photons, persistent from the times of matter-antimatter annihilations, thus are propagating freely on light geodetic trajectories through the spacetime geometry of the expanding universe up to the present days.

Assuming that at the times before recombination matter and photons coexisted in perfect thermodynamical equilibrium, despite the expansion of the cosmic volume (we shall come back to this problematic point in the next section), then this allows one to expect that these cosmic photons initially had a spectral distribution according to a perfect black-body radiator, that is, a Planckían spectrum. It is then generally concluded that a perfectly homogeneous Planckían radiation in an expanding universe stays rigorously Planckían over all times that follow. At this point one, however, one has to emphasize that this conclusion can only be drawn if (a) the initial spectrum really is perfectly Planckiàn and if (b) the universe is perfectly homogeneous and expands in the highest symmetrical form possible, that is, the one described by the so-called Robertson-Walker spacetime geometry.

Then it can be demonstrated (e.g., see [7]) that the Planckían character of the CMB spectral photon density initially given by

()

where dn_r(λ) denotes the spectral photon density at the time of recombination per wavelength interval dλ at wavelength λ and T_r is the temperature of the Planck radiation at this time, is conserved for all ongoing periods of the expanding universe.

Readers should, however, keep in mind that this is only guaranteed, if the universe has isotropic curvature and expands in a homologous, Robertson-Walker symmetric manner. (see, e.g., [8]). Due to this fact it then turns out that the initially Planckían spectral photon density changes with time so that for all cosmic future it maintains its Planckìan character, however, associated to a cosmologically reduced temperature T < T_r. On one hand at a later time t photons appear cosmologically redshifted to a wavelength λ^′ = λ(R/R_r), and on the other hand they are redistributed to a space volume increased by a factor (R/R_r) ³. Taking both effects together shows that at a later time t > t_r the resulting spectrum is given by

()

which with the help of Wien’s displacement law T · λ = const reveals that at later times it again is a Planck spectrum, however, with temperature T = T_r · (R_r/R). This already indicates that the present-day CMB should be associated to a temperature T₀ given by T₀ = T_r · (R_r/R₀) where the quantities indexed with “0” are those associated to the universe at the present time t = t₀. Depending on cosmic densities at the recombination phase the temperature T_r should have been between 3500 K and 4500 K (see [9]). This indicates that with the present-day CMB value of T₀ = 2.735 K [1] a ratio of cosmic expansion scales of

()

is disputable.

The abovementioned theory of a homologous cosmic expansion then also allows to derive an expression for the cosmic CMB temperature as a function of the cosmic photon redshift z = (λ₀ − λ_e)/λ_e at which astronomers are seeing distant galactic objects. Here λ₀ is the wavelength which is observed at present, that is, at us, while the associated wavelength λ_e is emitted at the distant object. With the validity of the cosmological redshift relation in a Robertson-Walker universe,

()

where R_e and R₀ denote the cosmic scale parameters at the time t_e when the photon was emitted from the distant galaxy and at the present time t₀. Thus one obtains by definition

()

This relation taken together with Wien’s law of spectral shift λ_max · T_CMB = 0.3 in this context is expressed by

()

then finally allows to write the CMB temperature as the following function of redshift:

()

2.2. Particle Distribution Functions in Expanding Spacetimes

Usually it is assumed that at the recombination era photons and matter, that is, electrons and protons in this phase of the cosmic evolution, are dynamically tightly bound to each other and undergo strong mutual interactions via Coulomb collisions and Compton collisions. These conditions are thought to then evidently guarantee a pure thermodynamical equilibrium state, implying that particles are Maxwell distributed and photons have a Planckian blackbody distribution. It is, however, by far not so evident that these assumptions really are fulfilled. This is because photons and particles are reacting to the cosmological expansion very differently; photons generally are cooling cosmologically being redshifted, while particles in first order are not directly feeling the expansion, unless they feel it adiabatically by mediation through numerous Coulomb collisions, which are relevant here in a fully ionized plasma before recombination, like they do in a box with subsonic expansion of its walls. But Coulomb collisions have a specific property which is highly problematic in this context.

This is because Coulomb collision cross sections are strongly dependent on the particle velocity v, namely, being proportional to (1/v⁴) (see [10]). This evidently causes that high-velocity particles are much less collision-dominated compared to low-velocity ones; they are even collision-free at supercritical velocities v ≥ v_c. So while the low-velocity branch of the distribution may still cool adiabatically and thus feels cosmic expansion in an adiabatic form, the high-velocity branch in contrast behaves collision-free and hence changes in a different form. This violates the concept of a joint equilibrium temperature and of a resulting Maxwellian velocity distribution function and means that there may be a critical evolutionary phase of the universe, due to different forms of cooling in the low- and high-velocity branches of the particle velocity distribution function, which do not permit the persistence of a Maxwellian equilibrium distribution to later cosmic times.

In the following part of the paper we demonstrate that even if a Maxwellian distribution would still prevail at the beginning of the collision-free expansion phase, that is, the postrecombination phase era, it would not persist in the universe during the ongoing of the collision-free expansion. For that purpose let us first consider a collision-free population in an expanding Robertson-Walker universe. It is clear that due to the cosmological principle and, connected with it, the homogeneity requirement, the velocity distribution function of the particles must be isotropic, that is, independent on the local place, and thus of the following general form:

()

where n(t) denotes the cosmologically varying density only depending on the worldtime t and

is the normalized, time-dependent isotropic velocity distribution function with the property:

If we assume that particles, moving freely with their velocity v into the

-associated direction over a distance l, are restituting at this new place, despite the differential Hubble flow and the explicit time-dependence of f, a locally prevailing covariant, but perhaps form-invariant distribution function f^′(v^′, t^′), then the associated functions f(v^′, t) and f(v, t) must be related to each other in a very specific way. To define this relation needs some special care, since particles that are freely moving in an homologously expanding Hubble universe do in this case at their motions not conserve their associated phasespace volumes d⁶ϕ = d³vd³x, since no Lagrangian exists and thus no Hamiltonian canonical relations for their dynamical coordinates v and x are valid. Hence Liouville’s theorem then requires that the conjugated differential phase space densities are identical; that is,

()

At the place where they arrive after passage over a distance l the particle population has a relative Hubble drift given by v_H = l · H coaligned with

, where H = H(t) means the time-dependent Hubble parameter. Thus the original particle velocity v is locally turned to v^′ = v − l · H. All dimensions of the space volume within a time Δt are cosmologically expanded, so that dx^′ = dx(1 + HΔt) holds. Complete reintegration into the locally valid distribution function then implies, with linearizably small quantities Δt≃l/v and Δv = −l · H, that one can express the above requirement in the following form:

()

This then means for terms of first order that

()

and thus

()

or the following requirement:

()

Looking first here for interesting velocity moments of the function f fulfilling the above partial differential equation by multiplying this equation with (a) 4πv²dv and (b) (4π/3)mv⁴dv and integrating over velocity space then leads to

a : n = n₀exp⁡(−2H(t − t₀)),
and
b : P = P₀exp⁡(−4H(t − t₀))

which then immediately makes evident that with the above solutions one finds that

()

is not constant, meaning that no adiabatic behaviour of the expanding gas occurs and that the gas entropy S also is not constant but decreasing and given by

()

It is perhaps historically interesting to see that assuming Hamilton canonical relations to be valid the Liouville theorem would then instead of (9) simply require f^′(v^′, t) = f(v, t) and hence would lead to the following form of a Vlasow equation:

()

In that case the first velocity moment is found with

()

yielding

()

which agrees with n ~ R⁻³. Looking also for the higher moment P then leads to

()

which now in this case shows that

()

That means in this case an adiabatic expansion is found, however, based on wrong assumptions!

Now going back to the correct Vlasow equation (13) one can then check whether or not this equation allows that an initial Maxwellian velocity distribution function persists during the ongoing collision-free expansion. Here we find for f ~ nT^−3/2exp⁡[−mv²/2KT], n and T being time-dependent, that one has

()

leading to the following Vlasow requirement (see (13)):

()

In order to fulfill the above equation obviously the terms with v² have to cancel each other, since n and T are velocity moments of f, hence independent on v. This is evidently only satisfied, if the change of the temperature with cosmic time is given by

()

This dependence in fact is obtained when inspecting the earlier found solutions for the moments n and P (see (13) and (14)), because these solutions exactly give

()

With that the above requirement (22) then only reduces to

()

which then leads to

()

making it evident that this requirement is not fulfilled and thus meaning that consequently a Maxwellian distribution cannot be maintained, even not at a collision-free expansion.

This finally leads to the statement that a correctly derived Vlasow equation for the cosmic gas particles leads to a collision-free expansion behaviour that neither runs adiabatic nor does it conserve the Maxwellian form of the distribution function f. Under these auspices it can, however, also easily be demonstrated (see [11]) that collisional interaction of cosmic photons with cosmic particles via Compton collisions in case of non-Maxwellian particle distributions does unavoidably lead to deviations from the Planckian blackbody spectrum. This makes it hard to be convinced by a pure Planck spectrum of the CMB photons at the time t_rec around the cosmic matter recombination.

Let us therefore now look into other basic concepts of cosmology to see whether perhaps also there problems can be identified which should caution cosmologists.

2.3. Can the Cosmological CMB Cooling Be Confirmed?

In the following part of the paper we now want to investigate whether or not the cosmological cooling of the CMB photons, freely propagating in the expanding Robertson-Walker space time geometry, can be confirmed by observations. The access to this problem is given by the connection that in an expanding universe at earlier cosmic times the CMB radiation should have been hotter according to cosmological expectations, for example, as derived in [7]. Hence the decisive question is whether it can be confirmed that the galaxies at larger redshifts, that is, those seen at times in the distant past, really give indications that they in fact are embedded in a correspondingly hotter CMB radiation environment. For that purpose one generally uses appropriate, so-called CMB radiation thermometers like interstellar CN-, CH-, or CO-molecular species (see [3, 12, 13], or [4]).

Assuming that molecular interstellar gas phases within these galaxies are in optically thin contact to the CMB that actually surrounds these galaxies allows one to assume that such molecular species are populated in their electronic levels according to a quasistationary equilibrium state population. In this respect especially interesting are molecular species with an energy splitting of vibrational or rotational excitation levels i, j that correspond to mean energies of the surrounding CMB photons; that is, E_i − E_j = hν_CMB. Under such conditions the relative level populations n_i, n_j essentially are given by the associated Boltzmann factor

()

where g_i,j are the state multiplicities. In the years of the recent past interstellar CO-molecules have been proven to be best suited in this respect as highly appropriate CMB thermometers. This was demonstrated by Srianand et al. [3] and Noterdaeme et al. [4].

The carbon monoxide molecule CO splits into different rotational excitation levels according to different rotational quantum numbers J. According to these numbers a splitting of CO lines occurs with transitions characterized by ΔJ = 1. In this respect the transition J = 1 → J = 0 leads to a basic emission line at λ_1,0 = 2.6 mm (i.e., ν₀ = 115, 6 GHz). The CO-molecule is biatomic with a rotation around an axis perpendicular to the atomic interconnection line. The quantum energies E_rot(J) are given by

()

where I is the moment of inertia of the CO-rotator and is given by

()

Here a is the interconnection distance, and m_C, m_O are the masses of the carbon and oxygen atom, respectively. S(J) is the angular momentum of the state with quantum number J, and ω(J) is the associated angular rotation frequency. The emission wavelengths from the excited states of the CO-A-X bands (J ≥ 2) thus are given by

()

Usually it is hardly possible to detect these CO-fine structure emissions from distant galaxies directly, due to their weaknesses and due to the strong perturbations and contaminations in this frequency range by the infrared (i.e., ≥115 GHz). Instead the relative population of these rotational fine structure levels can much better be observed in absorption appearing in the optical range. To actually use such a constellation to determine the relative populations of CO fine structure levels one needs a broadband continuum emitter in the cosmic background behind a gas-containing galaxy in the foreground. As in case of the object investigated by Srianand et al. [3] the foreground galaxy is at a redshift of z_abs = 2.41837 illuminated by a background quasar SDSS J143912.04 + 111740.5. Then the CO fine structure lines appear in absorption at wavelengths between 4900 Å and 5200 Å and, by fitting them with Voigt-profiles, the relative populations (n(J_i)/n(J_j)) of these fine structure levels can be determined. Assuming now optically thin conditions of the absorbing gas with respect to CMB photons, one can assume that in a photostationary equilibrium these relative populations are connected with the abovementioned Boltzmann factor as

()

where now

is the CMB Planck temperature at cosmic redshift z_abs = 2.41837. On the basis of the abovementioned assumptions Srianand et al. [3], depending on the specific transitions which they fit, find CMB excitation temperatures of

K; and

K, while according to standard cosmology (see (7)) at a redshift z_abs = 2.41837 one should have a CMB temperature of

K, where

K is the present-day CMB temperature (see [14]).

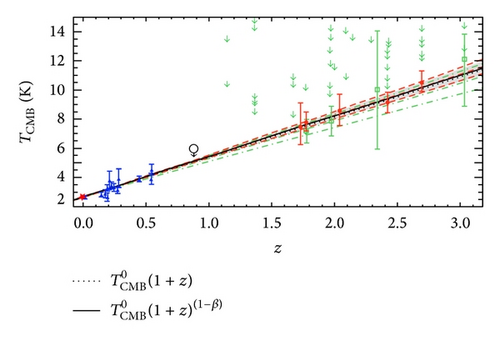
Though this clearly points to the fact that CMB temperatures at higher redshifts are indicated to be higher than the present-day temperature , it also demonstrates that the cosmologically expected value should have been a few percent higher than these fitted values. This, however, cannot question the applicability of the above described method in general, though some basic caveats have to be mentioned here.

First of all, observers with similar observations are often running into optically thick CO absorption conditions which will render the fitting procedure more difficult. Noterdaeme et al. [4], for instance, can show that the fitted CMB temperature differs with the CO-column density of the foreground absorber (see Figure 1). The determination of these column densities in itself is a highly nontrivial endeavour and only can be carried out assuming some fixed correlations between CO- and H₂-column densities, the latter being much better measurable.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

CO absorption profiles observed at SDSS-J1-70542 + 354340 (z_abs = 2.038); figure taken from Srianand et al. [3].

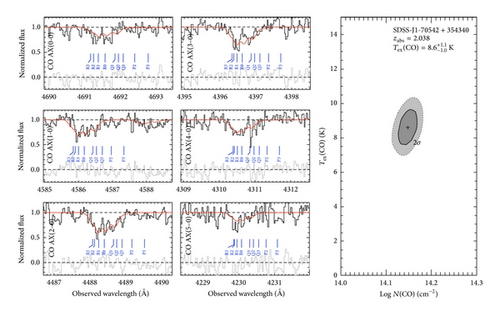
The second caveat in this context is connected with the assumption that relative populations of fine structure levels are purely determined by a photon excitation equilibrium with the surrounding CMB photons. If in addition any binary collisions with other molecules or any photons other than CMB photons are interfering into these population processes, then of course the fitted values have to be taken with correspondingly great caution. Especially in the infrared range delivering the relevant photons for excitations or deexcitations the CMB spectrum is strongly contaminated by galactic dust emissions [1, 15, 16]. Facing then the possibility that galaxies at higher redshifts are more pronounced in galactic dust emissions compared to our present galaxies nearby then makes CMB temperature determinations perhaps questionable. Nevertheless the results obtained by Noterdaeme et al. [4] when determining CO-excitation temperatures at foreground galaxies with different redshifts perhaps for most readers do convincingly demonstrate that a linear correlation of the CMB temperature with redshift can be confirmed (see Figure 2) as expected.

2.4. Problems with a Hot CMB in the Past

Though from the results displayed in the above Figure 2 it seems as if the cosmological CMB cooling with time can be surprisingly well confirmed, one nevertheless should not too carelessly take that as an observational fact. We remind the reader first to the theoretical prerequisites of a cosmologic CMB cooling reflected in a decrease of the Planck temperature T_CMB of this radiation: a Planckian spectrum only stays a Planckian, if

(a)
it was Planckian already at the beginning, that is, at the recombination phase, and if
(b)
since that time a completely homologous cosmic expansion took place till today.

Point (a) is questionable because the thermodynamic equilibrium state between baryons and photons in the early phase of fast cosmic expansion may quite well be disturbed or incomplete (see [7, 11], Section 2.2 of this paper). Point (b) is questionable, since at present times we find a highly structured, inhomogeneous cosmic matter distribution which does not originate from a homogeneous matter cosmos with a pure, unperturbed Robertson-Walker cosmic expansion.

The present universe actually is highly structured by galaxies, galaxy clusters, superclusters, and walls [17, 18]. Although perhaps the matter distribution was quite homogeneous at the epoch of the last scattering of cosmic photons when the CMB photons were in close contact to the cosmic matter, during the evolutionary times after that matter distribution has evidently become very inhomogeneous by the gravitational growth of seed structures. Thus fitting a perfectly symmetrical Robertson-Walker spacetime geometry to a universe with a lumpy matter distribution appears highly questionable [19]. This is an eminent general relativistic problem as discussed by Buchert [20], Buchert [21], Buchert [22], Buchert [23], Buchert [24], and Wiltshire [25]. If due to that structuring processes in the cosmic past and the associated geometrical perturbations of the Robertson-Walker geometry we would look back into direction-dependent different expansion histories of the universe, this would point towards associated CMB fluctuations (see [7]).

Thus it should be kept in mind that a CMB Planck spectrum is only seen with the same temperature from all directions of the sky, if in all these directions the same expansion dynamics of the universe took place. If CMB photons arriving from different directions of the sky have seen different expansion histories, then their Planck temperatures would of course be different and anisotropic, destroying completely the Planckian character of the CMB. This situation evidently comes up in case an anisotropic and nonhomologous cosmic expansion takes place like that envisioned and described in theories by Buchert [23], Buchert [26], Buchert [27], Buchert [24], or Wiltshire [25]. Let us check this situation by a simple-minded approach here: in the two-phase universe consisting of void and wall regions, as described by Wiltshire [25], void expansions turn out to be different from wall expansions, and, when looking out from the surface border of a wall region, in the one hemisphere one would see the void expansion dynamics, whereas in the opposite hemisphere one sees the wall expansion dynamics. Thus CMB photons arriving from the two opposite sides are differently cosmologically redshifted and thus in no case do constitute one common Planckian spectrum with one joint temperature T_CMB, but rather a bipolar feature of the local CMB-horizon.

In fact if one hemisphere expands different from the opposite hemisphere, then as a reaction also different CMB Planck temperatures would have to be ascribed to the CMB photons arriving from these opposite hemispherical directions. If, for instance, the present values of the characteristic scale in the two opposite hemispheres are R₁ and R₂, then this would lead to a hemispheric CMB temperature difference of ΔT_1,2 given by (see [7])

()

and would give an alternative to the present-day CMB-dipole explanation.

2.5. Hot CMB Impedes Gas Fragmentation

Stars are formed due to gravitational fragmentation of parts of a condensed interstellar molecular cloud. For the occurrence of an initial hydrostatic contraction of a self-gravitating primordial stellar gas cloud the radiation environmental conditions have to be appropriate. Cloud contraction, namely, can only continue as long as the contracting cloud can get rid of its increased gravitational binding energy by thermal radiation from the border of the cloud into open space. Hence in the following we show that in this respect the cloud-surrounding CMB radiation can take a critical control on that contraction process occurring or not occurring.

Here we simply start from the gravitational binding energy of a homogeneous gas cloud given by

()

where G is the gravitation constant, ρ is the mass density of the gas, R is the radius of the cloud, and M is the total gas mass of the cloud.

A contraction of the cloud during the hydrostatic collapse phase (see [28]) is only possible, if the associated change in internal binding energy E_B can effectively be radiated off to space from the outer surface of the cloud, that is, if

()

where σ_sb denote the Stefan-Boltzmann constant and T_c the thermal radiation temperature of the cloud, respectively.

This already makes evident that further contraction of the cloud is impeded, if the surrounding CMB temperature exceeds the cloud temperature, that is, if T_CMB > T_c, because then the only possibility is dR/dt ≥ 0!, that is, expansion! In order to calculate the radiation temperature T_c of the contracting cloud, one can determine an average value of the shrinking rate during this hydrostatic collapse phase by use of the following expression:

()

where τ_ff is the so-called free-fall time period of the cloud mass (see [29]). Thus from the above contraction condition together with this shrinking rate one thus obtains the following requirement for ongoing shrinking:

()

which allows to find the following value for the cloud temperature:

()

To give an idea for the magnitude of this cloud temperature T_c we here assume that the typical cloud mass can be adopted with M = 10 M_⊙ and that, for mass fragmentation of that size to occur, primordial molecular cloud conditions with an H₂−density of the order of ρ/2m = 10⁵ cm⁻³ must be adopted. With these values one then calculates a temperature of

()

This result must be interpreted as saying that as soon as in the past of cosmic evolution the CMB temperatures T_CMB were becoming greater than this above value T_c, then stellar mass fragmentations of masses of the order of M≃10 M_⊙ were not possible anymore. This would mean that galaxies at supercritical distances correlated with redshifts z ≥ z_c should not be able to produce stars with stellar masses larger than 10 M_⊙. This critical redshift can be easily calculated from the linear cooling relation and interestingly enough delivers . This means that galaxies at distances beyond such redshifts, that is, with z ≥ z_c = 2.09, should not be able to produce stars with stellar masses greater than 10 M_⊙.

If on the other hand it is well known amongst astronomers that galaxies with redshifts z ≥ z_c are known to show distant supernovae events [30], even serving as valuable cosmic light unit-candles and distance tracers, while such events just are associated with the collapse of 10 M_⊙-stars, then cosmology obviously is running into a substantial problem.

3. Conclusions

This paper hopefully has at least made evident that the “so-called” modern precision cosmology will perhaps not lead us directly into a complete understanding of the world and the evolution of the universe. Too many basic concepts inherent to the application of general relativity on describing the whole universe are still not settled on safe grounds, as we have pin-pointed in the foregoing sections of this paper.

We have shown in Section 2 of this paper that the cosmic microwave background radiation (CMB) only then can reasonably well be understood as a relict of the Big-Bang, if (a) it was already a purely Planckian radiation at the beginning of the recombination era, and if (b) the universe from that time onwards did expand rigorously isotropic and homologous according to a Robertson-Walker symmetrical expansion. As we have shown that, however, both points are highly questionable, since (a) matter and radiation are cooling differently in the expanding cosmos, so that the transition to the collisionless expansion induces a degeneration from thermodynamical equilibrium conditions with particle distribution functions deviating from Maxwellians and radiation distributions deviating from Planckians (see Section 2.2). Furthermore since (b) the cosmic expansion cannot have continued up to the present days in a purely Robertson-Walker-like style, otherwise no cosmic structures and material hierarchies could have formed.

It is hard to say anything quantitative at this moment what needs to be concluded from these results in Section 2.2. Fact is that during and after the phase of matter recombination in the universe Maxwellian velocity distributions for electrons and protons do not survive as Maxwellians but are degenerating into non-Maxwellian, nonequilibrium distributions, implying the drastic consequence that baryon densities are not falling off as (1/R³) but as (1/R²). The interaction of the originating CMB photons with nonequilibrium electrons by Compton collisions will then in consequence also change the resulting CMB spectrum to become a non-Planckian spectrum, as shown by Fahr and Loch [11]. Essentially the effect is that from Wien’s branch CMB photons are removed which instead reappear in the Rayleigh-Jeans branch.

The critical frequency limit is at around 10³ GHz, with effective radiation temperatures being reduced at higher frequencies with respect to those at lower frequencies. The exact degree of these changes depends on many things, for example, like the cosmologic expansion dynamics during the recombination phase and the matter density during this phase. However, the consequence is that the effective CMB radiation temperature measured at frequencies higher than 10³ GHz are lower than CMB temperatures at frequencies below 10³ GHz. Our estimate for conventionally assumed cosmologic model ingredients (Omegas!) would be by about 1K!

Unfortunately CMB measurements at frequencies beyond 10³ GHZ are practically absent up to now and do not allow to identify these differences. If in upcoming time periods, on the basis of upcoming better measurements in the Wien’s branch of the CMB, no such differences will be found, then the conclusions should not be drawn that the theoretical derivations of such changes presented here in our manuscript must be wrong, but rather that the explanation of the CMB as a relict radiation of the recombination era may be wrong.

Though indeed, as we discuss in Section 2.3, there are indications given by cosmic radiation thermometers like CN-, CO-, or CH-molecules that the CMB radiation has been hotter in the past of cosmic evolution, we also point out, however, that alternative explanations of these molecule excitation data like by collisional excitations and by infrared excitations through dust emissions should not be overlooked and that the conventionally claimed, redshift-relatedly hotter CMB in the past (i.e., following the relation T_CMB ~ (1 + z)T_0,CMB) in fact brings astrophysicists rather into severe problems in understanding the origin of massive stars in distant galaxies seen at large redshifts z ≥ z_c (see Section 2.5).

For those readers interested in more hints why the conventional cosmology could be in error, we are presenting other related controversial points in the Appendices.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Appendices

A. Behaviour of Cosmic Masses and Influence on Cosmology

All massive objects in space have inertia, that is, react with resistance to forces acting upon them. Physicists and cosmologists as well do know this as a basic fact, but nearly none of them puts the question why this must be so. Even celestial bodies at greatest cosmic distances appear to move, as if they are equipped with inertia and only resistantly react to cosmic forces. It nearly seems, as if nothing real exists that is not resistant to accelerating forces. While this already is a mystery in itself, it is even more mysterious what dictates the measure of this inertia. One attempt to clarify this mystery goes back to Newton’s concept of absolute space and the motions of objects with respect to this space. According to I. Newton, inertial reactions proportional to objects’ masses always appear, when the motion of these objects is to be changed. However, this concept of absolute space is already obsolete since the beginning of the last century. Instead modern relativity theory only talks about inertial systems (IRF) being in a constant, nonaccelerated motion. Amongst these all IRF systems are alike and equally suited to describe physics. Inertia thus must be something more basic which was touched by ideas of Mach [31] and Sciama [32]. In the following we shall follow these pioneering ideas a little more.

A.1. Linear Masses and Scima’s Approach to Mach’s Idea

Velocity and acceleration of an object can only be defined with respect to reference points, like, for example, another object or the origin of a Cartesian coordinate system. An acceleration with respect to the empty universe without any reference points does, however, not seem to make physical sense, because in that case no change of location can be defined. A reasonable concept instead would require to define accelerations with respect to other masses or bodies in the universe. But which masses should be serving as reference points? All? Perhaps weighted in some specific way? Or only some selected ones? And how should a resistance at the object’s acceleration with respect to all masses in the universe be quantifiable? This first thinking already show that the question of inertia very directly brings one into deepest calamities. The first more constructive thinking in this respect were started with the Austrian physicist Mach in 1883 (see [31]). For him any rational concept must ascribe inertia to the phenomenon appearing as resistance with respect to accelerations relative to all other bodies in the universe. Thus inertia cannot be taken as a genuine quantity of every body, rather inertia must be a “relational” quantity imprinted to each body by the existence and constellation of all other bodies in the universe, a so-called inertial interdependence between all bodies. This principle of mutual interdependence has been called Mach’s inertial principle, and the fathers of relativity and cosmology always were deeply moved by this principle, though they all never managed to construct a cosmologic theory which did fulfill Mach’s principle (see [33]).

The English physicist Sciama [32], however, tried to take serious the Machian principle and looked for a Machian formulation of inertial masses. With the help of an enlarged gravity theory, expanded in Maxwellian analogy to scalar and vectorial gravity potentials, he tried to show that inertia of single objects depends on all other masses in the universe up to its greatest distances. Sciama’s ideas go back to earlier concepts of Thomson [34] and Searle [35] and start with introducing a scalar potential, Φ, and a vector potential, , for the complete description of the cosmic gravitational field. The vector potential thereby describes the gravitational action of mass currents , and each moving object in the universe immediately is subject to the field of these cosmic mass currents which are intimately connected with the object’s own motion. Here and denote the mass density and its bulk motion, respectively.

In a homogeneous matter universe with mass density

the scalar field potential Φ for a test particle at rest is given by

()

where the upper integration border is the mass horizon r_∞ = c/H. Furthermore the vector potential

in a homogeneous and homologously expanding Hubble universe vanishes, since

()

In contrast, for a moving particle the scalar potential Φ is the same as for the test particle at rest; however, the vector potential

now is given by

()

The gravitoelectromagnetic fields

and

seen by the moving particle thus are

()

Assuming an additional body with mass M at a distance

from the test particle, where

may be taken as collinear to

, then leads to the following total gravitational force acting on the test particle:

()

Considering Newton’s second law, describing the gravitational attraction between two masses, it then requires for

that the following relation is valid:

()

and thus indicates that the apparent inertial mass of the test particle is proportional to Φ and thus ultimately is associated with the very distant cosmic masses. The inertial mass m_j of this test object j at a cosmic place r_j, when replacing density by distributed masses m_i, is represented by the expression

()

where again here ρ is the cosmic mass density and r is the distance to the cosmic mass source with the volume dV. The above summation runs over all other objects “i” in cosmic space besides that with index “j.” Hereby it turns out that according to Sciamaś theory the required inertial masses m_j are related to all other cosmic masses m_i and their inverse distances (1/r_i). Hence this formulation fulfills Mach’s basic idea, that is, its ideological request.

To enable this argumentation a Maxwellian analogy of gravity to electromagnetism was adopted. This, however, seems justified through papers like those by Fahr [36] and Fahr and Sokaliwska [37] were it is shown that the anomalous gravity needed for stably rotating disk galaxies and needed for conformal invariance of gravity fields with respect to special relativistic transformations do require the gravitational actions of mass currents.

A.2. Centrifugal Masses

It furthermore appears that mass constellations in the universe do also play the decisive role at centrifugal forces acting on rotating bodies. Accelerations are not only manifested, when the velocity of the object changes in the direction parallel to its motion (linear acceleration), but also if the velocity changes its direction (directional acceleration) without changing its magnitude (e.g., in case of orbital motions of planets). Under these latter conditions the inertia at rotational motions leading to centrifugal forces can be tested. The question here is what determines the magnitude of such centrifugal forces? Newton with his famous thought experiment of a water-filled rotating bucket (see, e.g., [9, 38]) had intended to prove that, what counts in terms of centrifugal forces, is the motion or rotation relative to the absolute space. According to Mach [31] centrifugal forces rather should, however, be a reaction with respect to physically relevant massive reference points in the universe. Thus also inertia with respect to centrifugal forces is a Machian phenomenon and again is a relational quantity connected with the constellation of other cosmic masses.

According to Mach the reaction of the water in the rotating bucket in forming a parabolic surface is an inertial reaction to centrifugal forces due to the rotation with respect to the whole universe marked by cosmic mass points, the so-called cosmic rest frame (see, e.g., [33]). Since the earth rotates, centrifugal forces act, and the earth’s ocean produces a centrifugal bulge at the equator with a differential height of about 10 m. The question what determines the exact magnitude of these centrifugal forces is generally answered: the rotation period of the earth! But this answer just now contains the real basic question: namely, the rotation period τ_Ω with respect to what? To the moon? To the sun? To the center of the galaxy? It easily turns out that it only makes sense to talk about rotation with respect to the stellar firmament, that is, the fixstar horizon. Why however just these most distant stars at a rotation should determine the inertial reaction of the earth’s ocean? While this again would prove the Machian constellation of the universe, it nevertheless is hard to give any good reason for that. Perhaps the only elucidating answer was given by Thirring [39] who started out from the principle of the relativity of rotations requiring that identical physical phenomena should be described irrelevant from what reference the description is formulated.

Thus, whether one describes the earth as rotating with respect to the universe at rest, or the universe as counterrotating with respect to the earth at rest, should lead to identical phenomena, that is, identical forces. To test this expectation Thirring [39] gave a general-relativistic description of the rotating universe and calculated geometrical perturbation forces induced by this rotating universe.

Within a Newtonian approximation of general relativity he could show that a rotating universe at the surface of the earth leads to metrical perturbation forces which are similar to centrifugal forces of the rotating earth. For a rigorous identity of both systems, (a) rotating earth and (b) rotating universe, a special requirement must, however, be fulfilled (see Figure 3).

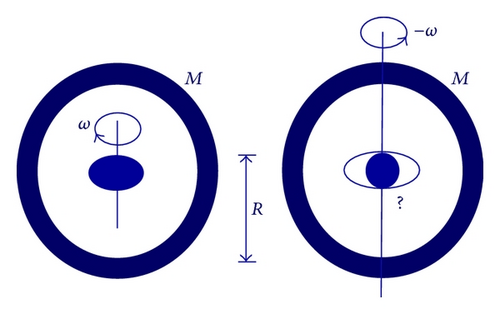
To carry out his calculations he needed to simplify the mass constellation in the universe. In his case the whole universe was represented by an infinitely thin, rotating spherical mass shell with radius R_U and a homogeneous mass deposition M_U representing the whole mass of the universe. Fahr and Zoennchen [9] have shown that this strongly artificial assumption can be easily relaxed to a universe represented as an extended system of spherical mass shells and still leads to Thirring’s findings; namely, that a full equivalence of the systems, (a) earth rotating and (b) universe rotating, only exists, if the ratio (M_U/R_U) is a constant, where M_U is the total mass of the universe within the cosmic mass horizon R_U = c/H₀ increasing proportional with the increasing age of the universe. Here c is the light velocity, and H₀ denotes the present Hubble constant.

However, this request would have very interesting consequences for an expanding Hubble universe with R_U being time-dependent and increasing with worldtime t as R_U(t) = c/H(t). It would, namely, mean that the equivalence of rotations in an expanding universe can only be and stay valid, if the mass of the universe increases with time such that (M_U,0/R_U,0) = M_U(t)/R_U(t) stays constant, that is, if the mass M_U increases linearly with R_U. This is an exciting and also wonderful result at the same time, because on one hand it is absolutely surprising to have a hint for an increasing world mass, and on the other hand it fulfills Mach’s idea of inertia in a perfect way. The above request, related to every single mass in the universe would, namely, require that its mass varies, if all ambient cosmic masses increase their cosmic distances, unless these masses change linearly with their changing distances. The same result would also come out from the analysis presented by Sciama [32] (see Appendix A) which lead to a mass m_j of the object j given by all other masses m_j by the expression

()

If now in addition with Thirring’s relation in a homologously expanding universe one can adopt that

()

We obtain the result that both Machian effects on inertia taken together just guarantee a constant inertia of every single object in the universe.

B. What Is the Mass of the Universe?

Following Mach [31] inertial masses of cosmic particles are not of a particle-genuine character but have relational character and are determined by the constellation of other cosmic masses in the universe (see reviews by Barbour and Pfister [33], Barbour [40], Wesson et al. [41], and Jammer and Bain [42]). Einstein at his first attempts to develop his field equations of general relativity was deeply impressed by Mach’s principle, but later in his career he abandoned it [43]. Up to the present days it is debated whether or not Einstein’s GR theory can be called a “Machian” or a “non-Machian” theory. At least some attempts have been made to develop an adequate form of a “relational,” that is, Machian, mechanics [8, 44–47]. In particular the requested scale-dependence of cosmic masses is unclear, though perhaps suggested by symmetry requirements or general relativistic action principle arguments given by arguments discussed by Hoyle [48], Hoyle [49], Hoyle [50], Hoyle et al. [51], and Hoyle et al. [52] along the line of the general relativistic action principle.

As we have shown above Thirring’s considerations of the nature of centrifugal forces were based on the concept of the mass of the universe M_U. To better understand Thirring’s result that this mass M_U should vary with the radius R_U of the universe, one should have a clear understanding of how this world mass might conceptually be defined, instead simply treating it as a mere number. Most rational would be to conceive M_U as a space-like summation of all masses in the universe, that is, an expression representing the space-like sum over all cosmic masses, present in the universe at the same event of time. In a uniform universe this number M_U is independent on the selected reference point. This means M_U represents the space-like sum of all masses simultaneously surrounding this point within its associated mass horizon. If at the time t a cosmic mass density ρ(t) prevails, then the whole mass integral up to the greatest distances has to be carried out using this density ρ(t), disregarded the fact that more distant region are seen at earlier cosmic times.

Fahr and Heyl [53], in order to calculate this space-like sum, considered an arbitrary spacepoint surrounded by cosmic mass shells all characterized by an actual mass density ρ = ρ₀. The situation is similar to a point in the center of a star being surrounded by mass shells with a stellar density, in the stellar case variable with central distance. For the cosmic case the spacegeometry of this space-like mass system is then given by the inner Schwarzschild metric. Under these auspices the quantity M_U as shown by Fahr and Heyl [53] is given by the following expression:

()

where the function in the numerator of the integrand is given by the following metrical expression:

()

The space-like metric in this cosmic case is given by an inner Schwarzschild metric, however, with the matter density given by the actual cosmic density ρ₀ and taking into account the fact that cosmic matter in a homologously expanding universe equipped with the Hubble dynamics leads to a relativistic mass increase taken into account by a cosmic Lorentz factor γ(r) = (1 − (H₀r/c) ²) ⁻¹. Assuming that within the integration border Hubble motions are subrelativistic one may evaluate the above expression with γ(r) = 1.

Then the above expression for M_U shows that real-valued mass contributions are collected up to a critical outer radius which one may call the local Schwarzschild infinity r = R_U defined by that point-associated Schwarzschild mass horizon which is given by (see [53])

()

This result is very interesting since meaning that this mass horizon distance R_U appears related to the actual cosmic mass density by the expression

()

and as evident from carrying out the integration in (B.2) leads to a point-associated mass M_U of the universe given by

()

This not only points to the surprising fact that with the use of the above concept for M_U Thirring’s relation in (B.1) is in fact fulfilled but also proves that Mach’s idea on the basis of this newly introduced definition of the mass M_U of the universe can be put on a solid basis.

C. A Physically Logic Conception of Empty Spacetime

The correct treatment of empty space in cosmology needs an answer to the following fundamental problem: What should a priori be expectable from empty space and how to formulate uncontroversial conditions for it and its physical behaviour? The main point to pay attention to is perhaps that the basic mechanical principle which was pretty clear at Newton’s epoch of classical mechanics, namely, “actio = reactio”, should somehow also still be valid at times of modern cosmology. So if at all the energy of empty space causes something to happen, then that “something” should somehow react back to the energy of empty space. Thus an action without any backreaction contains a conceptual error, that is, a misconception. That means, if empty space causes something to change in terms of spacegeometry, because it represents some energy that serves as a source of spacetime geometry, perhaps since space itself is energy-loaded, then with some evidence this vacuum-influenced spacegeometry should change the energy-loading of space (see [54–56]). There is, however, a direct hint that modern precision cosmology [1] does not respect this principle. This is because the modern Λ-cosmology describes a universe carrying out an accelerated expansion due to the action of vacuum pressure, while the vacuum energy density nevertheless is taken to be constant. (e.g., see [57]). How could a remedy of this flaw thus look like?

The cosmological concept of vacuum has a long and even not yet finished history (see, e.g., [41, 54, 58–64]). Due to its energy content, this vacuum influences spacetime geometry, but it is not yet clear in which way specifically. Normal baryonic or darkionic matter (i.e., constituted by baryons or dark matter particles, darkions, resp.) general-relativistically act through their associated energy-momentum tensors

and

(e.g., see [65]). Consequently it has been tried to also describe the GRT action of an energy-loaded vacuum introducing an associated hydrodynamical energy-momentum tensor

in close analogy to that of matter. The problem, however, now is that in these hydrodynamical energy-momentum tensors the contributing substances are treated as fluids described by their scalar pressures and their mass densities. The question then evidently arises what is vacuum pressure p_vac and what is vacuum mass density ρ_vac? Not going deeper into this point at the moment, one nevertheless then can give the tensor

in the following form (see, e.g., [38]):

()

where U_λ are the components of the vacuum fluid 4-velocity vector and g_μν is the metrical tensor. If now, as done in the so-called Λ-cosmology (see [1]), vacuum energy density is considered to be constant, then the following relation between mass density and pressure of the vacuum fluid can be derived ρ_vacc² = −p_vac (e.g., see [38, 57]). Under these prerequisites the vacuum fluid tensor

attains the simple form

()

The above term for

for a constant vacuum energy density ρ_vac can be combined with the famous integration constant Λ that was introduced by Einstein [66] into his GRT field equations and then formally leads to something like an “effective cosmological constant”:

()

Under this convention then the following interesting chance opens up, namely, to fix the unknown and undefined value of Einstein’s integration constant Λ so that the absolutely empty space, despite its vacuum energy density ρ_vac = ρ_vac,0 does not gravitate at all or curve spacetime, because this completely empty space is just described by a vanishing effective constant (i.e., pure vacuum does not curve spacetime):

()

Very interesting implications connected with that view are discussed by Overduin and Fahr [38], Fahr [54], or Fahr and Heyl [55]. It, for instance, implies that a completely empty space does not accelerate its expansion but can stagnate and leave cosmic test photons without permanently increasing redshifts and that on the other hand a matter-filled universe with a vacuum energy density different from ρ_vac,0 leads to an effective value of Λ_eff which now in general does not need to be constant. It nevertheless remains a hard problem to determine this function Λ_eff for a matter-filled universe in which a matter-polarized vacuum (see [56]) different from the vacuum of the empty space prevails. In the following we briefly discuss general options one has to describe this vacuum.

If vacuum is addressed, as done in modern cosmology, as a purely spacetime- or volume-related quantity, it nevertheless is by far not evident that “vacuum energy density” should thus be a constant quantity, simply because the unit of space volume is not a cosmologically relevant quantity. It may perhaps be much more reasonable to envision that the amount of vacuum energy of a homologously comoving proper volume DV is something that does not change its magnitude at cosmological expansions because this proper volume is a cosmologically relevant quantity. This new view then, however, would mean that the cosmologically constant quantity, instead of vacuum energy density ϵ_vac, is the vacuum energy within a proper volume given by

()

where g₃ is the determinant of the 3D-space metric.

In case of a Robertson-Walker geometry this is given by

()

Here K is the curvature parameter and R = R(t) is the time-dependent scale of the universe. The differential 3-space volume element in normalized polar coordinates is given by d³V = dr dϑ dφ and thus leads to

()

If de_vac now is taken as a cosmologically constant quantity, then it evidently requires that vacuum energy density has to change like

()

The invariance of the vacuum energy per comoving proper volume, de_vac, is a reasonable requirement, if this energy content does not do work on the dynamics of the cosmic geometry, especially by physically or causally influencing the evolution of the scale factor R(t) of the universe.

If, on the other hand, work is done by vacuum energy influencing the dynamics of the cosmic spacetime (either by inflation or deflation), as is always the case for a nonvanishing energy-momentum tensor, then automatically thermodynamic requirements need to be fulfilled, for example, relating vacuum energy density and vacuum pressure in a homogenous universe by the most simple standard thermodynamic relation (see [65]):

()

This equation is fulfilled by a functional relation of the form

()

for a scale-dependent vacuum energy density in the form ϵ_vac ~ R^−ν. Then it is evident that the above thermodynamic condition, besides for the trivial case ν = 3 when vacuum does not act (since: p_vac(ν = 3) = 0!, i.e., pressure-less vacuum), is as well fulfilled by other values of ν, as, for instance, by ν = 0, that is, a constant vacuum energy density ϵ_vac ~ R⁰ = const.

The exponent ν is, however, more rigorously restricted, if under more general cosmic conditions the above thermodynamic expression (C.9) needs to be enlarged by a term describing the work done by the expanding volume against the internal gravitational binding in this volume. For mesoscalic gas dynamics (aerodynamics, meteorology, etc.) this term is generally of no importance; however, for cosmic scales there is definitely a need for this term. Under cosmic perspectives this term for binding energy is an essential quantity, as, for instance, evident from star formation theory, and has been quantitatively formulated by Fahr and Heyl [55] and Fahr and Heyl [67]. With this term, the enlarged thermodynamic equation (C.9) then attains the following completed form:

()

where the last term on the RHS accounts for internal gravitational binding energy of the vacuum. With this term the above thermodynamic equation can also tentatively be solved by the p_vac = −((3 − ν)/3)ϵ_vac which then leads to

()

As evident, however, now the above relation is only fulfilled by ν = 2!, prescribing that the corresponding cosmic vacuum energy density must vary and only vary like

()

expressing the fact that under these general conditions vacuum energy density should fall off with R⁻², instead of being constant.

If we then take all these results together, we see that not only the mass density in the Robertson-Walker cosmos but also the vacuum energy density should scale with R⁻². The first to conclude from this is that the vacuum pressure p_vac under this condition should behave like prescribed by the thermodynamic equation (C.9):

()

and thus under the new auspices given now yield

()

meaning that now the following polytropic relation holds

()

meaning that again a negative pressure for the vacuum is found but smaller than in the case of constant vacuum energy density.

With the additional points presented in the Appendices it may all the more become evident that modern cosmology has to undergo a substantial reformation.

References

1 Bennett C. L., Hill R. S., Hinshaw G., Nolta M. R., Odegard N., Page L., Spergel D. N., Weiland J. L., Wright E. L., Halpern M., Jarosik N., Kogut A., Limon M., Meyer S. S., Tucker G. S., and Wollack E., First-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: foreground emission, Astrophysical Journal, Supplement Series. (2003) 148, no. 1, 97–117, https://doi.org/10.1086/377252, 2-s2.0-0242390240.
10.1086/377252
Web of Science® Google Scholar
2 Ade P. A. R., Aghanim N., Armitage-Caplan C. et al., Planck 2013 results. XVI. Cosmological parameters, http://arxiv.org/abs/1303.5076.
Google Scholar
3 Srianand R., Gupta N., Petitjean P., Noterdaeme P., and Saikia D. J., Detection of the 2175 Å extinction feature and 21-cm absorption in two Mg II systems at z ∼ 1.3, Monthly Notices of the Royal Astronomical Society Letters. (2008) 391, no. 1, L69–L73, https://doi.org/10.1111/j.1745-3933.2008.00558.x, 2-s2.0-66549117169.
10.1111/j.1745-3933.2008.00558.x
Web of Science® Google Scholar
4 Noterdaeme P., Petitjean P., Srianand R., Ledoux C., and López S., The evolution of the cosmic microwave background temperature: measurements of T_CMB at high redshift from carbon monoxide excitation, Astronomy & Astrophysics. (2011) 526, no. 11, article L7, https://doi.org/10.1051/0004-6361/201016140, 2-s2.0-78650919748.
10.1051/0004-6361/201016140
Google Scholar
5 Penzias A. A. and Wilson R. W., A Measurement of excess antenna temperature at 4080 Mc/s, The Astrophysical Journal. (1965) 142, 419–421, https://doi.org/10.1086/148307.
10.1086/148307
Web of Science® Google Scholar
6 Smoot G., Theoretical and observational aspects of the CMB, Cosmology 2000, 2000.
Google Scholar
7 Fahr H. J. and Zönnchen J. H., The ‘writing on the cosmic wall’: is there a straightforward explanation of the cosmic microwave background?, Annalen der Physik. (2009) 18, no. 10-11, 699–721, https://doi.org/10.1002/andp.200910365, 2-s2.0-70350416779.
10.1002/andp.200952110-1104
CAS Google Scholar
8 Goenner H. F. M., J. B. Barbour and H. Pfister, Mach′s principle and theories of gravitation, Mach′s Principle: From Newton′s Bucket to Quantum Gravity, 1995, Birkhäuser.
Google Scholar
9 Fahr H. J. and Zoennchen J. H., Cosmological implications of the Machian principle, Naturwissenschaften. (2006) 93, no. 12, 577–587, https://doi.org/10.1007/s00114-006-0133-y, 2-s2.0-33751404615.
10.1007/s00114-006-0133-y
CAS PubMed Web of Science® Google Scholar
10 Spitzer L., Physics of Fully Ionized Gases, 1956, Interscience Publishers.
Google Scholar
11 Fahr H. J. and Loch R., Photon stigmata from the recombination phase superimposed on the cosmological background radiation, Astronomy & Astrophysics. (1991) 246, 1–9.
CAS Web of Science® Google Scholar
12 Bahcall J. N. and Wolf R. A., Fine-structure transitions, The Astrophysical Journal. (1968) 152, https://doi.org/10.1086/149589.
10.1086/149589
Google Scholar
13 Meyer D. M. and Jura M., A precise measurement of the cosmic microwave background temperature from optical observations of interstellar CN, The Astrophysical Journal. (1985) 297, 119–132, https://doi.org/10.1086/163509.
10.1086/163509
CAS Web of Science® Google Scholar
14 Mather J. C., Fixsen D. J., Shafer R. A., Mosier C., and Wilkinson D. T., Calibrator design for the COBE Far Infrared Absolute Spectrophotometer (FIRAS), Astrophysical Journal Letters. (1999) 512, no. 2, 511–520, https://doi.org/10.1086/306805, 2-s2.0-0033585688.
10.1086/306805
Google Scholar
15 Hauser M. G., Arendt R. G., Kelsall T., Dwek E., Odegard N., Weiland J. L., Freudenreich H. T., Reach W. T., Silverberg R. F., Moseley S. H., Pei Y. C., Lubin P., Mather J. C., Shafer R. A., Smoot G. F., Weiss R., Wilkinson D. T., and Wright E. L., The COBE diffuse infrared background experiment search for the cosmic infrared background. I. Limits and detections, The Astrophysical Journal. (1998) 508, no. 1, 25–43, https://doi.org/10.1086/306379, 2-s2.0-33645557562.
10.1086/306379
Web of Science® Google Scholar
16 Henry R. C., Diffuse background radiation, The Astrophysical Journal. (1999) 516, L49–L52, https://doi.org/10.1086/312003.
10.1086/312003
CAS Web of Science® Google Scholar
17 Geller M. J. and Huchra J. P., Mapping the universe, Science. (1989) 246, no. 4932, 897–903, https://doi.org/10.1126/science.246.4932.897, 2-s2.0-0041142467.
10.1126/science.246.4932.897
CAS PubMed Web of Science® Google Scholar
18 Ellis R. S., J. Paul, T. Montmerle, and E. Aubourg, Galaxy formation, Proceedings of the 19th Texas Symposium on Relativistic Astrophysics, December 1998, Paris, France.
Google Scholar
19 Wu K. K. S., Lahav O., and Rees M. J., The large-scale smoothness of the Universe, Nature. (1999) 397, no. 6716, 225–230, https://doi.org/10.1038/16637, 2-s2.0-0033590542.
10.1038/16637
CAS Web of Science® Google Scholar
20 Buchert T., Cosmogony of generic structures, Publications of the Beijing Astronomical Observatory, 1995, 1, 59–70.
Google Scholar
21 Buchert T., P. Coles, V. Martinez, and M.-J. Pons-Borderia, Averaging hypotheses in Newtonian cosmology, Mapping, Measuring, and Modelling the Universe, 1996, 94, Astronomical Society of the Pacific, Astronomical Society of the Pacific Conference Series.
Google Scholar
22 Buchert T., R. Bender, T. Buchert, P. Schneider, and F. von Feilitzsch, Averaging inhomogeneous cosmologies—a dialogue, Research in Particle-Astrophysics—Proceedings, 1997, Max-Planck-Institut für Astrophysik, Garching, Germany, 71–82.
Google Scholar
23 Buchert T., On average properties of inhomogeneous cosmologies, General Relativity and Gravitation. (2001) 33, 1381–1390, http://arxiv.org/abs/gr-qc/0001056.
10.1023/A:1012061725841
Web of Science® Google Scholar
24 Buchert T., Dark energy from structure: a status report, General Relativity and Gravitation. (2008) 40, no. 2-3, 467–527, https://doi.org/10.1007/s10714-007-0554-8, MR2375262, ZBL1137.83375, 2-s2.0-39149086704.
10.1007/s10714-007-0554-8
Web of Science® Google Scholar
25 Wiltshire D. L., Cosmic clocks, cosmic variance and cosmic averages, New Journal of Physics. (2007) 9, article 377, https://doi.org/10.1088/1367-2630/9/10/377, 2-s2.0-35748946355.
10.1088/1367-2630/9/10/377
Google Scholar
26 Buchert T., On average properties of inhomogeneous fluids in general relativity: perfect fluid cosmologies, General Relativity and Gravitation. (2001) 33, no. 8, 1381–1405, https://doi.org/10.1023/a:1012061725841, MR1863235, 2-s2.0-0035540268.
10.1023/A:1012061725841
Web of Science® Google Scholar
27 Buchert T., A cosmic equation of state for the inhomogeneous universe: can a global far-from-equilibrium state explain dark energy?, Classical and Quantum Gravity. (2005) 22, no. 19, L113–L119, https://doi.org/10.1088/0264-9381/22/19/l01, MR2176738, 2-s2.0-25444469413.
10.1088/0264-9381/22/19/L01
Web of Science® Google Scholar
28 Safronov V. S., Evolution of the Protoplanetary Cloud and Formation of the Earth and Planets, 1972.
Google Scholar
29 Jeans J. H., The planetesimal hypothesis, The Observatory. (1929) 52, 172–173.
Google Scholar
30 Perlmutter S., Aldering G., Goldhaber G., Knop R. A., Nugent P., Castro P. G., Deustua S., Fabbro S., Goobar A., Groom D. E., Hook I. M., Kim A. G., Kim M. Y., Lee J. C., Nunes N. J., Pain R., Pennypacker C. R., Quimby R., Lidman C., Ellis R. S., Irwin M., McMahon R. G., Ruiz-Lapuente P., Walton N., Schaefer B., Boyle B. J., Filippenko A. V., Matheson T., Fruchter A. S., Panagia N., Newberg H. J. M., Couch W. J., and The Supernova Cosmology Project, Measurements of omega and lambda from 42 high-redshift supernovae, The Astrophysical Journal. (1999) 517, 565–586, https://doi.org/10.1086/307221.
10.1086/307221
Web of Science® Google Scholar
31 Mach E., Die Mechanik in ihrer Entiwcklung: Eine historitsch kritische Darstellung, 1883, F.A. Brockhaus.
Google Scholar
32 Sciama D. W., On the origin of inertia, Monthly Notices of the Royal Astronomical Society. (1953) 113, no. 1, 34–42, https://doi.org/10.1093/mnras/113.1.34, MR0059668.
10.1093/mnras/113.1.34
Web of Science® Google Scholar
33 J. B. Barbour and H. Pfister, Mach′s Principle: From Newton′s Bucket to Quantum Gravity, 1995, Birkhäuser.
Google Scholar
34 Thomson J., On the electric and magnetic effects produced by the motion of electrified bodies, Philosophical Magazine. (1981) 11, 229–249.
Google Scholar
35 Searle G., On the steady motion of an electrified ellipsoid, Philosophical Magazine. (1897) 44, 329–341.
10.1080/14786449708621072
Google Scholar
36 Fahr H. J., The Maxwellian alternative to the dark matter problem in galaxies, Astronomy & Astrophysics. (1990) 236, 86–94.
Google Scholar
37 Fahr H.-J. and Sokaliwska M., The influence of gravitational binding energy on cosmic expansion dynamics: new perspectives for cosmology, Astrophysics and Space Science. (2012) 339, no. 2, 379–387, https://doi.org/10.1007/s10509-012-1002-0, 2-s2.0-84860588555.
10.1007/s10509-012-1002-0
CAS Google Scholar
38 Overduin J. and Fahr H.-J., Matter, spacetime and the vacuum, Naturwissenschaften. (2001) 88, no. 12, 491–503, https://doi.org/10.1007/s001140100258, 2-s2.0-0035216990.
10.1007/s001140100258
CAS PubMed Web of Science® Google Scholar
39 Thirring H., Über die Wirkung rotierender ferner Massen in der Einsteinschen Gravitationstheorie, Physikalische Zeitschrift. (1918) 19, 33–39.
Google Scholar
40 Barbour J. B., J. B. Barbour and H. Pfister, General relativity as a perfectly Machian theory, Mach′s Principle: From Newton′s Bucket to Quantum Gravity, 1995, Birkhäuser.
Google Scholar
41 Wesson P. S., Ponce de Leon J., Liu H., Mashhoon B., Kalligas D., Everitt C. W., Billyard A., Lim P., and Overduin J., A theory of space, time and matter, International Journal of Modern Physics A. (1996) 11, no. 18, 3247–3255, https://doi.org/10.1142/s0217751x96001553, MR1401193.
10.1142/S0217751X96001553
Google Scholar
42 Jammer M. and Bain J., Concepts of mass in contemporary physics and philosophy, Physics Today. (2000) 53, no. 12, 67–68, https://doi.org/10.1063/1.1341924.
10.1063/1.1341924
Google Scholar
43 Holtonl G. J., Einstein and the Search for Reality, 1970, 6.
Google Scholar
44 Dehnen H. and Hönl H., Finite universe and Mach′s principle, Nature. (1962) 196, no. 4852, 362–363, https://doi.org/10.1038/196362a0, 2-s2.0-0041779641.
10.1038/196362a0
Google Scholar
45 Hofmann W., J. B. Barbour and H. Pfister, Motion and inertia, Mach′s Principle: From Newton′s Bucket to Quantum Gravity, 1995, Birkhäuser.
Google Scholar
46 Reissner H., J. B. Barbour and H. Pfister, On the relativity of accelerations in mechanics, Mach′s Principle: From Newton′s Bucket to Quantum Gravity, 1995, Birkhäuser.
Google Scholar
47 Lynden-Bell D. and Katz J., Classical mechanics without absolute space, Physical Review D. (1995) 52, no. 12, 7322–7324, https://doi.org/10.1103/physrevd.52.7322, MR1375881, 2-s2.0-0002328670.
10.1103/PhysRevD.52.7322
CAS Google Scholar
48 Hoyle F., A new model for the expanding universe, Monthly Notices of the Royal Astronomical Society. (1948) 108.
10.1093/mnras/108.5.372
Google Scholar
49 Hoyle F., On the relation of the large numbers problem to the nature of mass, Astrophysics and Space Science. (1990) 168, no. 1, 59–88, https://doi.org/10.1007/BF00654594, 2-s2.0-33747192217.
10.1007/BF00654594
Web of Science® Google Scholar
50 Hoyle F., Mathematical theory of the origin of matter, Astrophysics and Space Science. (1992) 198, no. 2, 195–230, https://doi.org/10.1007/BF00644754, 2-s2.0-33747202651.
10.1007/BF00644754
Web of Science® Google Scholar
51 Hoyle F., Burbidge G., and Narlikar J. V., A quasi-steady state cosmological model with creation of matter, The Astrophysical Journal. (1993) 410, no. 2, 437–457, https://doi.org/10.1086/172761, 2-s2.0-0001721640.
10.1086/172761
CAS Web of Science® Google Scholar
52 Hoyle F., Burbidge G., and Narlikar J. V., Astrophysical deductions from the quasi-steady-state cosmology, Monthly Notices of the Royal Astronomical Society. (1994) 267, no. 4, 1007–1019, https://doi.org/10.1093/mnras/267.4.1007.
10.1093/mnras/267.4.1007
Web of Science® Google Scholar
53 Fahr H. J. and Heyl M., Concerning the instantaneous mass and the extent of an expanding universe, Astronomische Nachrichten. (2006) 327, no. 7, 733–736, https://doi.org/10.1002/asna.200510616, 2-s2.0-33746881872.
10.1002/asna.200510616
Web of Science® Google Scholar
54 Fahr H. J., The cosmology of empty space: how heavy is the vacuum?, Philosophy of Natural Sciences. (2004) 33, 339–353.
Google Scholar
55 Fahr H. J. and Heyl M., About universes with scale-related total masses and their abolition of presently outstanding cosmological problems, Astronomische Nachrichten. (2007) 328, no. 2, 192–199, https://doi.org/10.1002/asna.200610714, 2-s2.0-33847738233.
10.1002/asna.200610714
Web of Science® Google Scholar
56 Fahr H. J. and Sokaliwska M., Revised concepts for cosmic vacuum energy and binding energy: Innovative cosmology, Aspects of Todays Cosmology, 2011, 95–120, https://doi.org/10.5772/24505.
10.5772/24505
Google Scholar
57 Peebles P. J. and Ratra B., The cosmological constant and dark energy, Reviews of Modern Physics. (2003) 75, no. 2, 559–606, https://doi.org/10.1103/revmodphys.75.559, MR1973358, 2-s2.0-0038579350.
10.1103/RevModPhys.75.559
CAS Web of Science® Google Scholar
58 Blome H.-J. and Priester W., Vacuum energy in a Friedmann-Lemaître cosmos, Naturwissenschaften. (1984) 71, no. 10, 528–531, https://doi.org/10.1007/bf00455641, 2-s2.0-34250139038.
10.1007/BF00455641
Web of Science® Google Scholar
59 Fahr H. J., The modern concept of vacuum and its relevance for the cosmological models of the universe, Philosophy of Natural Sciences. (1989) 17, 48–60.
Google Scholar
60 Zeldovich I. B., Vacuum theory—a possible solution to the singularity problem of cosmology, Soviet Physics Uspekhi. (1981) 133, 479–503.
Google Scholar
61 Birrell N. D. and Davies P. C. W., Book-review—quantum fields in curved space, Science. (1982) 217.
Google Scholar
62 Lamoreaux S. K., Systematic correction for ‘demonstration of the Casimir force in the 0.6 to 6 micrometer range’, http://arxiv.org/abs/1007.4276.
Google Scholar
63 Barrow J. D., Guide to Performing Relative Quantitation of Gene Expression Using Real-Time Quantitative PCR, 2000, Applied Biosystems, Foster City, Calif, USA.
Google Scholar
64 Blome H. J., Hoell J., and Priester W., Kosmologie, Lehrbuch der Experimentalphysik, 2002, 8, Walter de Gruyter, Berlin, Germany, 439–582.
Google Scholar
65 Goenner H., Einfuehrung in die Spezielle und Allgemeine Relativitaetstheorie, 1996, Spektrum Akademischer, Heidelberg, Germany.
Google Scholar
66 Einstein A., Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie, Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften, 1917, Nabu Press, 142–152.
Google Scholar
67 Fahr H. and Heyl M., Cosmic vacuum energy decay and creation of cosmic matter, Naturwissenschaften. (2007) 94, 709–724.
10.1007/s00114-007-0235-1
CAS PubMed Web of Science® Google Scholar

Citing Literature

All articles

Remaining Problems in Interpretation of the Cosmic Microwave Background

Abstract

1. Introduction

2. Does Planck Stay Planck, If It Ever Was?

2.1. The Cosmic Microwave Background Tested by Cosmic Thermometers

2.2. Particle Distribution Functions in Expanding Spacetimes