Volume 2015, Issue 1 493452

Research Article

Open Access

A New Fractional-Order Based Intelligent Maximum Power Point Tracking Control Algorithm for Photovoltaic Power Systems

Kuo-Nan Yu,

Kuo-Nan Yu

Department of Electrical Engineering, National Chin-Yi University of Technology, Taichung 41170, Taiwan ncut.edu.tw

Search for more papers by this author

Chih-Kang Liao,

Chih-Kang Liao

Department of Electrical Engineering, National Chin-Yi University of Technology, Taichung 41170, Taiwan ncut.edu.tw

Search for more papers by this author

Her-Terng Yau,

Corresponding Author

Her-Terng Yau

[email protected]

orcid.org/0000-0002-1187-1771

Department of Electrical Engineering, National Chin-Yi University of Technology, Taichung 41170, Taiwan ncut.edu.tw

Search for more papers by this author

Kuo-Nan Yu,

Kuo-Nan Yu

Department of Electrical Engineering, National Chin-Yi University of Technology, Taichung 41170, Taiwan ncut.edu.tw

Search for more papers by this author

Chih-Kang Liao,

Chih-Kang Liao

Department of Electrical Engineering, National Chin-Yi University of Technology, Taichung 41170, Taiwan ncut.edu.tw

Search for more papers by this author

Her-Terng Yau,

Corresponding Author

Her-Terng Yau

[email protected]

orcid.org/0000-0002-1187-1771

Department of Electrical Engineering, National Chin-Yi University of Technology, Taichung 41170, Taiwan ncut.edu.tw

Search for more papers by this author

First published: 16 June 2015

https://doi.org/10.1155/2015/493452

Citations: 13

Academic Editor: Marcelo C. Cavalcanti

Share a link

Email
Wechat
Bluesky

Abstract

This paper proposes a new type of variable fractional-order incremental conductance algorithm (VFOINC), combined with extenics variable step size (EVSS) control into the maximum power point tracking (MPPT) design for photovoltaic power systems. At the beginning of maximum power tracking, the fractional-order number α is selected as 1; the good transient tracking characteristic of traditional incremental conductance method is used. When the maximum power point is approached, the fractional-order number α is selected as variable fractional order; the curve profile of α in fractional order is used to approximate, so that the system has good tracking effect in transient and steady states. The experimental and simulation results show that, compared with traditional incremental conductance method (INC) and fractional-order incremental conductance method (FOINC), this method has better MPPT effect.

1. Introduction

The green energy, including solar energy, wind energy, tide, and geothermal heat, has attracted considerable attention in recent years. Among those, solar energy is one of the cleanest energy sources as the solar radiant energy is converted into electric energy directly [1–5]. The present photovoltaic power systems have low conversion efficiency and high cost, and the power benefit varies with the climatic conditions and ambient temperature. There are some difficulties to be overcome. Due to nonlinearity of the power and voltage of photovoltaic power systems, how to use the MPPT to maximize the output efficiency of photovoltaic power systems in any climatic conditions becomes an important issue.

In actual physical system, many phenomena reflect fractional-order behavior, such as heat transfer and electromagnetic wave in solid [6]. The solar cell is a sort of semiconductor material (single crystalline silicon); the characteristic when the power generated by photocurrent crosses P-N junction (energy gap) reflects the nonlinear characteristic of photovoltage and photocurrent. The interaction between the diffusion current and drift current of semiconductor and the ambient temperature can be described by fractional order [7].

Many MPPT technologies have been implemented in photovoltaic power systems in previous literatures, such as voltage feedback method, power feedback method, INC [8–10], and perturbation and observation (P&O) [11–16]. This paper proposes combining VFOINC with EVSS [17] for tracking the maximum power point. In terms of the selection of derivative order number α, at the beginning of maximum power tracking, α is selected as 1; the good transient tracking characteristic of INC is used. When the maximum power point is approached, α is selected as variable fractional order; the curve profile of α in fractional order is used to approximate, so that the system has good tracking effect in transient and steady states. The experimental and simulation results show that the VFOINC + EVSS method proposed in this paper uses DC/DC boost converter to adjust the duty cycle; compared with the INC and FOINC, the VFOINC + EVSS proposed in this paper can shorten the time for MPPT, so that the efficiency of photovoltaic power systems is increased.

2. Brief Introduction to Photovoltaic Power Systems

The solar cell is P-N junction semiconductor structure converting solar energy into electric energy. The photovoltaic panel is composed of many solar cells connected in parallel and in series, as shown in Figure 1. The current be expressed as

()

where I is the output current of photovoltaic panel, V is the output voltage of photovoltaic panel, q is the electric quantity of electron, I_ph is the current, I_sat is the reverse saturation current, T is the battery temperature, n_p is the parallel number of photovoltaic panels, n_s is the serial number of photovoltaic panels, k is the Boltzmann constant, and A is the ideal factor coefficient of P-N junction. I_sat is sensitive to the temperature, expressed as

()

where T_r is the reference temperature at ordinary temperature (25°C), I_r is the reverse saturation current of semiconductor at ordinary temperature, E_G is the energy in energy gap, I_sc is the short-circuit current of semiconductor at ordinary temperature, k_sc is the temperature coefficient of short-circuit current, and S is the irradiance. The output power of photovoltaic power system can be represented by P = VI; the power-voltage (P-V) curve and voltage-current (I-V) characteristic curve of photovoltaic power system are shown in Figure 2.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Internal equivalent diagram of photovoltaic panel.

The MPPT is carried out in order to reach the peak point of nonlinear curve, the photovoltaic power system is connected to a boost converter, and the duty cycle of switch is controlled by the voltage and current generated by photovoltaic power system, so as to implement MPPT. The basic structure diagram [11–16] of the converter is shown in Figure 3. When the switch is “on,” the photovoltaic power system charges the inductor via the switch. When the switch is “off,” the photovoltaic power system releases the inductive energy to the load via diode. Adjusting the duty cycle changes input voltage and current, so as to change the output voltage and current. When the switch is off t_on and on t_off, the current through the inductor can be expressed as

()

The duty ratio (D) of control switch is

()

As the one-cycle voltage variation of inductor is 0, that is,

, the equation of output voltage V_o can be obtained:

()

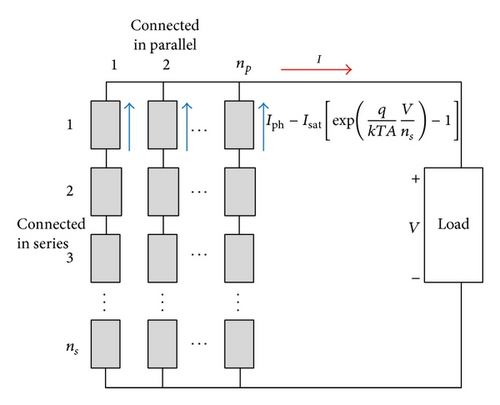
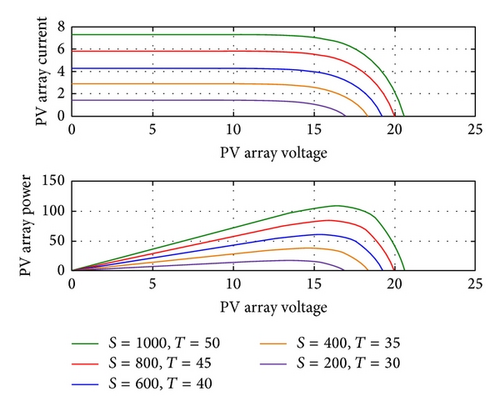
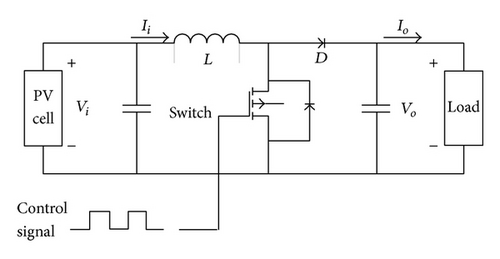
Among multiple solar power system MPPT methods, the P&O is most extensively used [11–16] due to simple structure and few parameters required, and the parameters of characteristic curve of photovoltaic power system are not required. However, this method uses periodic perturbation, so there will be oscillation at the maximum power point, causing some unnecessary power loss. The INC is proposed in order to overcome this defect.

The INC is based on power-voltage (P-V) curve of solar cell, meeting one of the following equations at maximum power point:

()

where I_o and V_o are the current and voltage captured at previous time point, respectively, and ΔI and ΔV are the current and voltage variations in unit time, respectively. However, in the process of MPPT, the magnitude of offset ΔV determines the speed of reaching MPP and the perturbation after the MPP is reached. The decision depends on the user. However, the VFOINC + EVSS [17] proposed in this paper can use the mathematical model in fractional-order form to describe the diffusion phenomenon of solar cell at different temperatures. In terms of MPPT speed, the EVSS is used to improve the tracking speed and the perturbation in steady state.

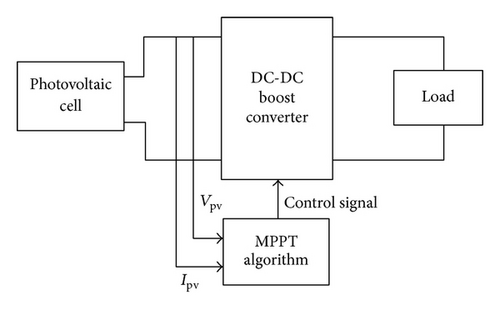
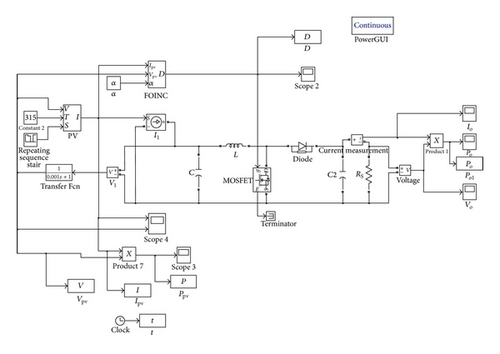
The photovoltaic power system architecture proposed in this paper is shown in Figure 4. The photovoltaic panel connects the output voltage and current to the DC-DC boost converter directly, and the MPPT is used to control signal and adjust the duty cycle of switching pulse width modulation (PWM). Finally, the DC-DC boost converter is connected to the load to measure the system output power.

3. Design of Algorithm and Control Method

This paper uses MATLAB R2010a Simulink to build the simulated photovoltaic power system architecture and to design the control method. Figure 5 shows the photovoltaic power system simulation built by this paper. The module FOINC can be replaced by different MPPTs for duty cycle control of different switching pulse adjustment control methods.

3.1. Fractional-Order Differentiator

The fractional-order differentiator is often applied to signal processing, adaptive control, active control, and linear and nonlinear feedback control. At present, many computing applications of fractional-order derivative have been proposed; according to the definition of Riemann–Liouville and Grunwald–Letnikov [18–20], general fractional-order differentiator can be expressed as

()

where γ() represents γ function and α is the order number of derivative, when its value is 0 < α < 1, representing physical phenomenon of fractional order, for example, heat transfer and electromagnetic wave in solid [6]. The solar cell is a sort of semiconductor material (single crystalline silicon). The characteristic when the power generated by photocurrent crosses the P-N junction (energy gap) reflects the nonlinear characteristic of photovoltage and photocurrent. The interaction between the diffusion current and drift current of semiconductor and the ambient temperature can be described by fractional order.

3.2. Variable Fractional-Order Incremental Conductance Method

General fractional-order differentiator can be expressed as (8); when the INC is used, (7) can be expressed as

()

If α > 0, the geometric interpretation of fractional order can be represented as Figure 6. The slope is a straight line when α = 1, that is, general first derivative. Therefore, 0 < α < 1 presents the form of fractional-order derivative, approximately to curve form, referring to literature [21]. The result of using (8) in the right part of (7) is

()

where res(γ, −z) = (−1) ^z/z!, z = 0, −1, −2, −3, …, and γ(0) = res(γ, 0), and res represents the residue in complex plane. As the traditional INC tracks maximum power fast and the curve of fractional-order differentiator INC nearby MPP approximates MPPT, the steady-state tracking effect is better than general INC. Therefore, this paper proposes using variable derivative value α in Figure 4 for calculation of MPPT. It has good response to transient MPPT and steady-state MPP sweeping, so as to increase the overall efficiency of photovoltaic power system.

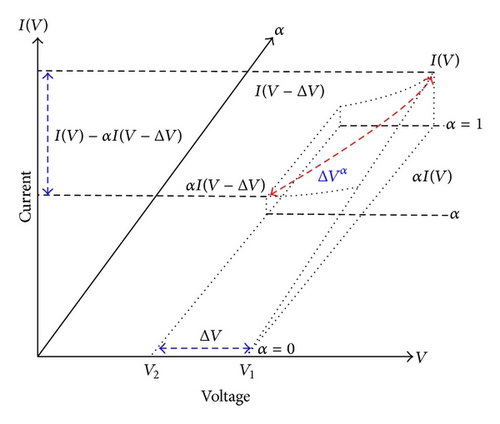
This paper uses voltage V and current I and power P as calculated variance in captured signal, voltage, and current, ΔV = V − V_o, ΔI = I − I_o, and the slope is the slope (ΔP/ΔV) of power-voltage curve of solar cell; the variation of partial voltage and current of fractional-order differentiator approximates as d^αI = I − αI₀ and . In terms of selection of derivative order number α, at the beginning of MPPT, α is selected as 1; the good transient tracking characteristic of traditional INC is used. When the MPP is approached, α is selected as variable fractional-order form, and the curve profile of α in fractional order is used to approximate, so that the system has good tracking effect in transient and steady states.

3.3. Extenics Variable Step Size (EVSS)

The offset ΔV during MPPT of traditional INC determines the tracking speed and the perturbation accuracy when the MPP is reached. In comparison to traditional MPPT algorithm, the variable step size control has gradually increased or decreased offset ΔV variable of step size, so as to improve the tracking speed and stability. For detailed variable step size control, please refer to [20].

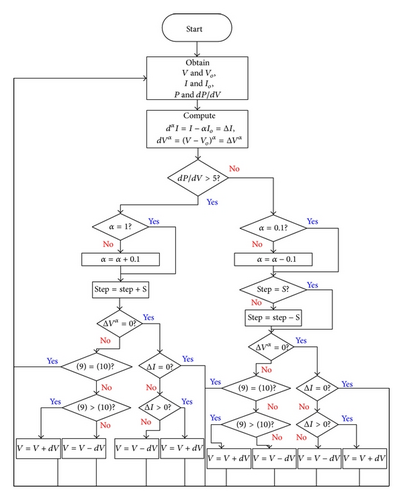
As the variable step size control has variable step size nearby MPP, there will be voltage perturbation problem nearby MPP. Therefore, this paper proposes adding extenics theory in the variable step size control [22, 23] to deduce the EVSS. The voltage, power, and slope are captured as reference frame, so that the minimum step size can be used for perturbation nearby the MPP, increasing the efficiency of photovoltaic power system. The control flow of VFOINC + EVSS proposed in this paper is shown in Figure 7.

4. Simulation Analysis Results and Comparison

This paper uses MATLAB R2010a Simulink to build the model and controller of photovoltaic power system. This simulation is the comparison of different states of irradiance and temperature and step size. Figure 8 shows the curve test of photovoltaic power system at specific temperature and irradiance, including voltage-power (P-V) curve, current-voltage (I-V) curve, duty ratio (cycle) (D), and tracking number curves.

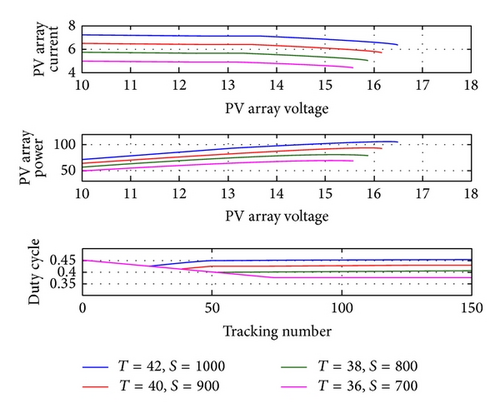
The first simulated condition is irradiance 1000 kW/m² and temperature 25°C; the other condition is irradiance decreasing from 1000 kW/m² to 900 kW/m² and then decreasing to 200 kW/m² and increasing to 1000 kW/m², and the INC, FOINC, and VFOINC + EVSS are compared.

According to the simulation result in Figure 9, as the step size of INC depends on the user, the speed and accuracy are limited to some extent. However, in the same step size, the transient tracking speed of INC is better than FOINC. In terms of the combination of VFOINC and EVSS, Figure 10 shows the combination of good transient tracking efficiency of traditional INC and steady-state stability of VFOINC and EVSS; it is observed that the VFOINC + EVSS proposed in this paper has better MPPT simulation curve in transient and steady states.

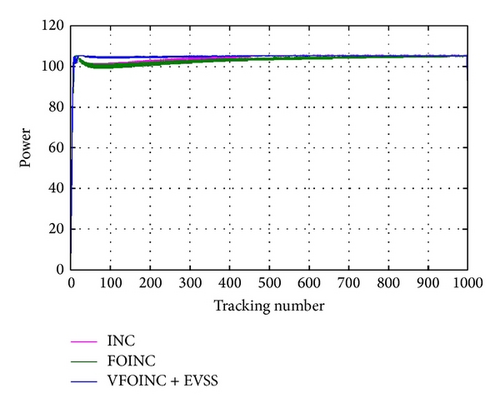
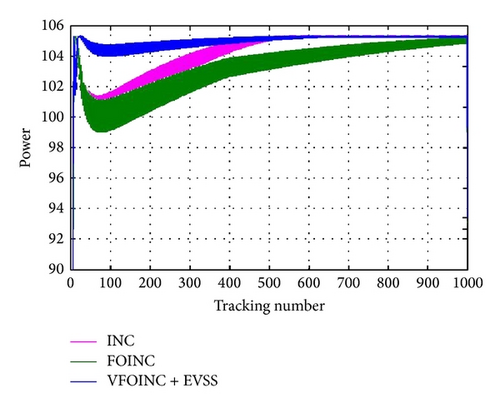
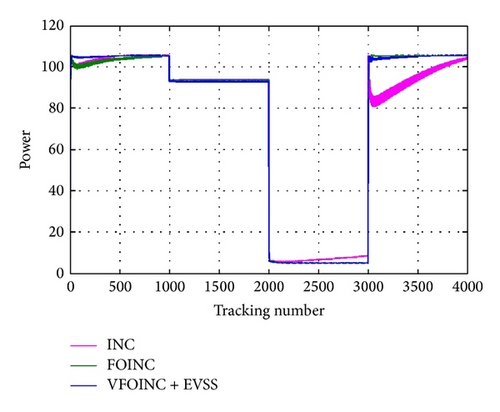
The second simulated condition is the irradiance decreasing from 1000 kW/m² to 900 kW/m² and then decreasing to 200 kW/m² and increasing to 1000 kW/m², as shown in Figure 11. The INC, FOINC, and VFOINC + EVSS are compared. The variance in α is shown in Figure 12.

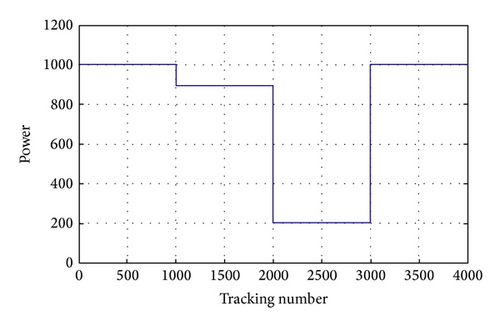
Figure 12 shows the variance in α. It is observed that, at the start of simulation, as the system is just started up, letting α = 1 for tracking MPP, the form of INC is used for tracking; α is reduced to 0.1 gradually when MPP is approached, so that the system uses INC in transient state and uses VFOINC in steady state. In addition, in terms of α variation when the tracking number is 1000, 2000, and 3000, the MPP shifts as the irradiance changes; the system increases α value again to increase the tracking speed and reduces it to 0.1 again when the MPP is approached, so that the transient and steady-state response curves have better effect.

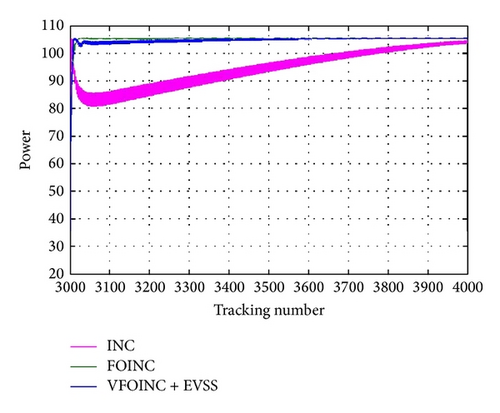
Figure 13 shows the simulation result, and Figure 14 shows that the step size of INC still depends on the user; the speed and accuracy are limited to some extent, so that the MPPT always costs a long time in the case of variable irradiance, causing unnecessary power loss. The VFOINC + EVSS proposed in this paper can improve the excessive tracking number of traditional INC algorithm in the case of variable irradiance, so that the system has better curve.

5. Experimental Results

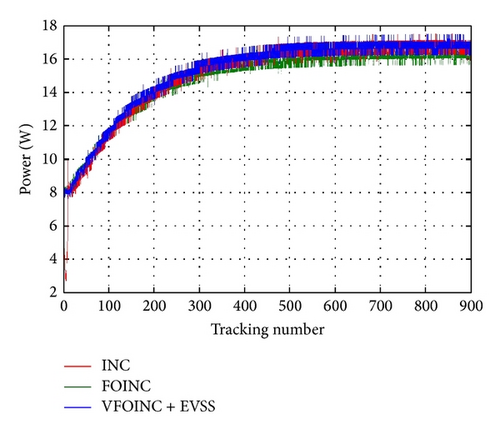
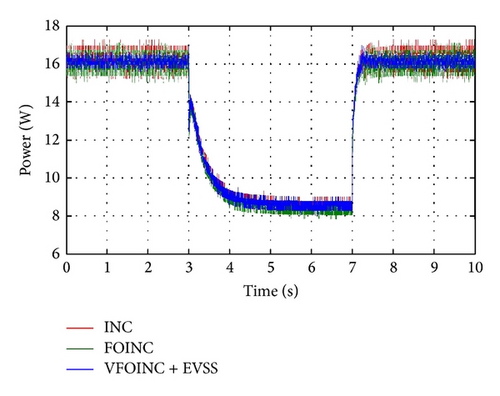
In order to show the efficiency of this scheme in real solar cell system, the performance of the proposed controller was evaluated experimentally and was compared with INC method and FOINC method. The specification of the experimental solar panel is shown in Table 1. Figure 15 shows the experimental results obtained for the output power given a uniform irradiance of 1000 W/m². From the results, it can be seen that VFOINC + EVSS has better tracking rates than traditional INC and in terms of the steady-state response it is also good and has the same effect. In order to show that this scheme is robust to the irradiance, the results of irradiances changed from 1000 kW/m² to 400 kW/m² and then increased to 1000 kW/m² as shown in Figure 16. Our results are also consistent with the results of the simulations. It can prove the feasibility of the proposed method.

Table 1. Specification of SYK17-18M solar panel.

P_max⁡	V_MPP	I_MPP	V_OC	I_SC
17 W	18 V	0.94 A	21.24 V	1.04 A

6. Conclusion

This paper uses VFOINC + EVSS for photovoltaic power system MPPT control, to improve the MPPT speed and steady-state perturbation of INC. In terms of selection of derivative order number α, at the start of MPPT, α is selected as 1; the good tracking characteristic of traditional INC in transient state is used. When the MPP is approximated, α is selected as variable fractional-order form; the curve profile of α in fractional order is used to approximate, so that the system has good tracking effect in transient and steady states. According to the simulation result of the algorithm, the transient and steady-state responses of the control method proposed in this study to photovoltaic MPPT system are better than those of INC and FOINC, meaning this method for MPPT can reduce unnecessary power loss of the system, so as to increase the generating efficiency of system.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

References

1 Hua C., Lin J., and Shen C., Implementation of a DSP-controlled photovoltaic system with peak power tracking, IEEE Transactions on Industrial Electronics. (1998) 45, no. 1, 99–107, https://doi.org/10.1109/41.661310, 2-s2.0-0032000579.
10.1109/41.661310
Web of Science® Google Scholar
2 Otieno C. A., Nyakoe G. N., and Wekesa C. W., A neural fuzzy based maximum power point tracker for a photovoltaic system, Proceedings of the IEEE AFRICON, September 2009, Nairobi, Kenya, 1, 6, https://doi.org/10.1109/afrcon.2009.5308552, 2-s2.0-74349111667.
10.1109/afrcon.2009.5308552
Google Scholar
3 Kwon J.-M., Kwon B.-H., and Nam K.-H., Grid-connected photovoltaic multistring PCS with PV current variation reduction control, IEEE Transactions on Industrial Electronics. (2009) 56, no. 11, 4381–4388, https://doi.org/10.1109/tie.2008.2010293, 2-s2.0-70350393898.
10.1109/TIE.2008.2010293
Web of Science® Google Scholar
4 Petrone G., Spagnuolo G., Teodorescu R., Veerachary M., and Vitelli M., Reliability issues in photovoltaic power processing systems, IEEE Transactions on Industrial Electronics. (2008) 55, no. 7, 2569–2580, https://doi.org/10.1109/tie.2008.924016, 2-s2.0-47049125539.
10.1109/TIE.2008.924016
Web of Science® Google Scholar
5 Wai R.-J., Wang W.-H., and Lin C.-Y., High-performance stand-alone photovoltaic generation system, IEEE Transactions on Industrial Electronics. (2008) 55, no. 1, 240–250, https://doi.org/10.1109/tie.2007.896049, 2-s2.0-38349017098.
10.1109/TIE.2007.896049
Web of Science® Google Scholar
6 Hwang C., Leu J.-F., and Tsay S.-Y., A note on time-domain simulation of feedback fractional-order systems, IEEE Transactions on Automatic Control. (2002) 47, no. 4, 625–631, https://doi.org/10.1109/9.995039, 2-s2.0-0036530321.
10.1109/9.995039
Web of Science® Google Scholar
7 Lin C.-H., Huang C.-H., Du Y.-C., and Chen J.-L., Maximum photovoltaic power tracking for the PV array using the fractional-order incremental conductance method, Applied Energy. (2011) 88, no. 12, 4840–4847, https://doi.org/10.1016/j.apenergy.2011.06.024, 2-s2.0-80052259329.
10.1016/j.apenergy.2011.06.024
Web of Science® Google Scholar
8 Hussein K. H., Muta I., Hoshino T., and Osakada M., Maximum photovoltaic power tracking: an algorithm for rapidly changing atmospheric conditions, IEE Proceedings: Generation, Transmission and Distribution. (1995) 142, no. 1, 59–64, https://doi.org/10.1049/ip-gtd:19951577, 2-s2.0-0029195477.
10.1049/ip-gtd:19951577
Web of Science® Google Scholar
9 Kwon J.-M., Nam K.-H., and Kwon B.-H., Photovoltaic power conditioning system with line connection, IEEE Transactions on Industrial Electronics. (2006) 53, no. 4, 1048–1054, https://doi.org/10.1109/TIE.2006.878329, 2-s2.0-33747587000.
10.1109/TIE.2006.878329
Web of Science® Google Scholar
10 Zhou X., Song D., Ma Y., and Cheng D., The simulation and design for MPPT of PV system based on incremental conductance method, Proceedings of the WASE International Conference on Information Engineering (ICIE ’10), August 2010, Hebei, China, 314–317, https://doi.org/10.1109/icie.2010.170, 2-s2.0-78049328525.
10.1109/icie.2010.170
Google Scholar
11 Mahdi A. J., Tang W. H., and Wu Q. H., Estimation of tip speed ratio using an adaptive perturbation and observation method for wind turbine generator systems, Proceedings of the IET Conference on Renewable Power Generation, September 2011, 1–6, https://doi.org/10.1049/cp.2011.0133, 2-s2.0-84856241098.
10.1049/cp.2011.0133
Google Scholar
12 Femia N., Petrone G., Spagnuolo G., and Vitelli M., A technique for improving P&O MPPT performances of double-stage grid-connected photovoltaic systems, IEEE Transactions on Industrial Electronics. (2009) 56, no. 11, 4473–4482, https://doi.org/10.1109/tie.2009.2029589, 2-s2.0-70350424434.
10.1109/TIE.2009.2029589
Web of Science® Google Scholar
13 Bratcu A. I., Munteanu I., Bacha S., Picault D., and Raison B., Cascaded DC-DC converter photovoltaic systems: power optimization issues, IEEE Transactions on Industrial Electronics. (2011) 58, no. 2, 403–411.
10.1109/TIE.2010.2043041
Web of Science® Google Scholar
14 Estébanez E. J., Moreno V. M., Pigazo A., Liserre M., and Dell’Aquila A., Performance evaluation of active islanding-detection algorithms in distributed-generation photovoltaic systems: two inverters case, IEEE Transactions on Industrial Electronics. (2011) 58, no. 4, 1185–1193, https://doi.org/10.1109/tie.2010.2044132, 2-s2.0-79952670231.
10.1109/TIE.2010.2044132
Web of Science® Google Scholar
15 Cecati C., Ciancetta F., and Siano P., A multilevel inverter for photovoltaic systems with fuzzy logic control, IEEE Transactions on Industrial Electronics. (2010) 57, no. 12, 4115–4125, https://doi.org/10.1109/tie.2010.2044119, 2-s2.0-77950332903.
10.1109/TIE.2010.2044119
Web of Science® Google Scholar
16 Femia N., Petrone G., Spagnuolo G., and Vitelli M., Optimization of perturb and observe maximum power point tracking method, IEEE Transactions on Power Electronics. (2005) 20, no. 4, 963–972, https://doi.org/10.1109/tpel.2005.850975, 2-s2.0-22944480226.
10.1109/TPEL.2005.850975
Web of Science® Google Scholar
17 Li J. and Wang H., A novel stand-alone PV generation system based on variable step size INC MPPT and SVPWM control, Proceedings of the IEEE 6th International Power Electronics and Motion Control Conference (IPEMC ’09), May 2009, 2155–2160, https://doi.org/10.1109/ipemc.2009.5157758, 2-s2.0-77951114393.
10.1109/ipemc.2009.5157758
Google Scholar
18 Podlubny I., Fractional Differential Equations, 1999, 198, Academic Press, New York, NY, USA, Mathematics in Science and Engineering, MR1658022.
Web of Science® Google Scholar
19 Ma C. and Hori Y., Fractional-order control: theory and applications in motion control, IEEE Industrial Electronics Magazine. (2007) 1, no. 4, 6–16, https://doi.org/10.1109/mie.2007.909703, 2-s2.0-37749018625.
10.1109/MIE.2007.4375295
Web of Science® Google Scholar
20 Kenneth S. K. and Bertram R., An Introduction to the Fractional Calculus and Fractional Differential Equations, 1993, John Wiley & Sons, New York, NY, USA.
Google Scholar
21 Das S., Functional Fractional Calculus for System Identification and Controls, 2008, Springer, Berlin, Germany, MR2414740.
Google Scholar
22 Chen W. and Chen R., The evaluation of scientific journals in Chinese Scientific Research based on extenics theory, Proceedings of the International Conference on Information Management, Innovation Management and Industrial Engineering, October 2012, 195–198, https://doi.org/10.1109/iciii.2012.6339631, 2-s2.0-84870659479.
10.1109/iciii.2012.6339631
Google Scholar
23 Hong-Chun S., Ze-Jiang H., Shi-Yun S., and Qing Y., The fault diagnosis algorithm for transformer based on Extenics and rough set theory, Proceedings of the 3rd International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT ’08), April 2008, Nanjing, China, 1269–1272, https://doi.org/10.1109/DRPT.2008.4523602.
10.1109/DRPT.2008.4523602
Google Scholar

Citing Literature

All articles

A New Fractional-Order Based Intelligent Maximum Power Point Tracking Control Algorithm for Photovoltaic Power Systems

Abstract

1. Introduction

2. Brief Introduction to Photovoltaic Power Systems

3. Design of Algorithm and Control Method

3.1. Fractional-Order Differentiator

3.2. Variable Fractional-Order Incremental Conductance Method

3.3. Extenics Variable Step Size (EVSS)

4. Simulation Analysis Results and Comparison

5. Experimental Results

6. Conclusion

Conflict of Interests

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A New Fractional-Order Based Intelligent Maximum Power Point Tracking Control Algorithm for Photovoltaic Power Systems

Abstract

1. Introduction

2. Brief Introduction to Photovoltaic Power Systems

3. Design of Algorithm and Control Method

3.1. Fractional-Order Differentiator

3.2. Variable Fractional-Order Incremental Conductance Method

3.3. Extenics Variable Step Size (EVSS)

4. Simulation Analysis Results and Comparison

5. Experimental Results

6. Conclusion

Conflict of Interests

References

Citing Literature

Figures

References

Related

Information