Simple Moving Voltage Average Incremental Conductance MPPT Technique with Direct Control Method under Nonuniform Solar Irradiance Conditions
Abstract
A new simple moving voltage average (SMVA) technique with fixed step direct control incremental conductance method is introduced to reduce solar photovoltaic voltage (VPV) oscillation under nonuniform solar irradiation conditions. To evaluate and validate the performance of the proposed SMVA method in comparison with the conventional fixed step direct control incremental conductance method under extreme conditions, different scenarios were simulated. Simulation results show that in most cases SMVA gives better results with more stability as compared to traditional fixed step direct control INC with faster tracking system along with reduction in sustained oscillations and possesses fast steady state response and robustness. The steady state oscillations are almost eliminated because of extremely small |dP/dV| around maximum power (MP), which verify that the proposed method is suitable for standalone PV system under extreme weather conditions not only in terms of bus voltage stability but also in overall system efficiency.
1. Introduction
Penetration of solar photovoltaic (PV) power in centralized or decentralized generation system has been evolving at a rapid pace in recent years and is considered to be one of the most promising power generation options among all renewable energy sources (RES) for sustainable energy development. But due to the intermittency of environmental conditions and nonuniform nature of solar irradiance it produces significant fluctuation in solar power generation. This is because solar irradiance is not highly correlated between even close locations at very short timescale which is one of the important factors in solar power generation output variability. Studies have shown that increased geographical diversity in solar PV generation system leads to decrease in the output power efficiency and sometimes generates hot-spots which causes damage to the solar cells [1]. So far power system operators accommodate solar and wind power variability through storage reserves to stabilize the power output levels [2]. Technically there are two ways to improve the efficiency of PV power generation: it could be possible either to develop low cost high efficiency solar conversion materials or to operate the PV system at maximum power point (MPP) for getting optimal output power. Because of the high cost of solar cells, it is necessary to operate the PV array at the maximum operating point. Therefore maximum power point tracking (MPPT) is considered as an essential part of PV generation system and is one of the key issues for researchers to reduce the effects of nonlinear characteristics of PV array [3].
So far different MPPT algorithms have been proposed for optimization of PV output power, such as perturb & observe (P&O) [4–6], incremental conductance (INC) [7, 8], hill climbing [9, 10], neural network, fuzzy logic theory, and genetic algorithm [11–13]. However it has been observed that most of the MPPT methods are developed by assuming that solar irradiance is applied on the entire PV array uniformly. Unfortunately, the nonlinearity of solar irradiation is directly effecting the PV characteristic because of multiple local maxima (the mismatching problem) which can be exhibited on current-voltage (IV curve) and power-voltage (PV curve) of solar PV array if the entire array does not receive uniform solar irradiation.
Although some researchers have worked on partially shaded condition (PSC) and fast changing solar irradiance MPPT [14–17], in [14], a two-stage MPPT with instant online Voc and Isc measurement was proposed. This MPPT is very simple to implement but an additional circuit is required to track the real maximum power point (RMPP) under nonuniform insolation conditions; a novel algorithm to track the global power peak (GPP) under partially shaded conditions based on several critical observations in conjunction with a DC-DC converter to accelerate the tracking speed with feed forward control is proposed in [15]. To ensure fast MPPT process with DC-DC converter duty cycle modulation under partial shading conditions and load variations with modified incremental conductance (INC) algorithm to track the GMPP is proposed in [16] and a modified incremental conductance algorithm under fast changing solar irradiance to reduce oscillation in solar module power at zero level and to mitigate the inaccurate response is discussed in [17].
Among all the aforementioned MPPT algorithms, incremental conductance (INC) and perturb & observe (P&O) are commonly used for small and large scale PV power plants because both the algorithms operate in accordance with power against voltage (P-V) curve of PV module and tune the duty cycle of converter to ensure the next MPP point accordingly. In P&O steady state oscillation occurred because perturbation continuously changes in both the directions to maintain MPP under rapidly changing solar irradiance which causes system to be less efficient and to have more power losses [6, 18]. However, the conventional incremental conductance method determines the slope of PV curve by varying the converter duty cycle in fixed or variable step size until the MPP is achieved and in this way oscillation under rapidly changing solar irradiance is reduced with greater efficiency but due to complicated algorithm speed is slow.
As discussed that nonlinear solar irradiance produces significant fluctuation in PV output voltage (VPV). So far, no considerable work is done to minimize the fluctuations of VPV terminal voltage of MPPT controller which is directly related to optimizing the efficiency and reducing the MPP tracking time. In this paper a direct control incremental conductance with simple moving voltage average (SMVA) technique is proposed. Using SMVA we examined the variability of VPV among different PV array configurations with nonuniform solar irradiance to aggregate the plant output at varying timescales. The simulation of proposed model is performed in MATLAB/Simulink and results are provided with comparison of conventional fixed step direct control incremental conductance method. The comparison results reveal that the proposed SMVA method provides better output by eliminating the steady state oscillations and greater output which is fast and accurate with response to variation of solar irradiation.
In Section 2 of this paper an overview about conventional and fixed step direct control INC is given and proposed SMVA technique is discussed in Section 3. Section 4 is about the case example and in Section 5 results are discussed, and finally in Section 6 conclusion is drawn.
2. Direct Control Incremental Conductance MPPT Method
Traditional conventional incremental conductance INC is based on two independent control loops as shown in Figure 1(a). The first loop uses the incremental and instantaneous conductance to generate the error signal, and the second is the closed loop with a proportional- integral (PI) controller to drive the error to zero at MPP according to (1). But in practical implementation of INC under nonuniform solar irradiance the slope of P-V characteristics curves (dP/dV ≠ 0) at MPP.
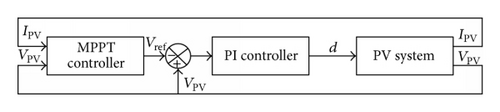
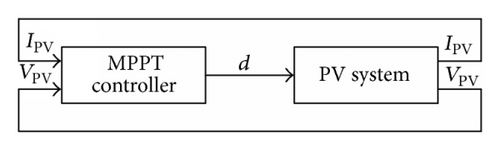
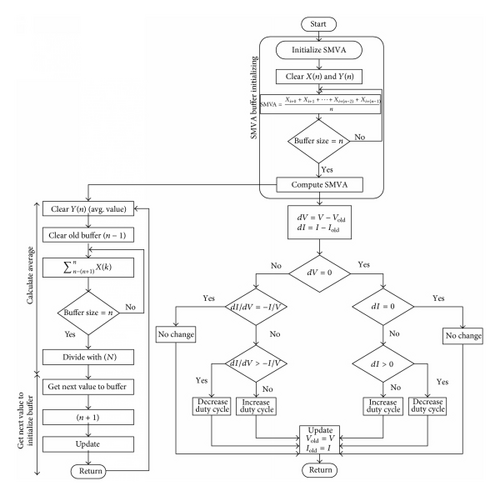
3. Proposed Method
In this paper a simple moving voltage average (SMVA) technique is proposed for recovering oscillatory effect such as ripple in solar PV generator voltage VPV under nonuniform solar irradiance. The proposed technique is inspired by advantages of practical simple moving average (SMA) model which is frequently used in financial markets to form a trend following indicator by reducing price fluctuations. Herein, SMVA does not predict price direction but rather defines the voltage direction with a lag because it is based on solar irradiation to compute and average the irradiation signal in time series analysis. The moving average is a simple low pass FIR (Finite Impulse Response) filter commonly used for smoothing an array of sampled data/signal; so far SMA is effectively used by different scholars [22, 23] in engineering characteristic reducing noise in random samples while retaining a sharp step response and computing the monitoring values to predict the future data.
Although several other soft computing methods have been developed, as we can find in the works of Stevenson and Porter [24], Hansun and Subanar [25–27], and Popoola et al. [28, 29], moving average method is still considered as the best method by many researchers due to its easiness, objectiveness, reliability, and usefulness.
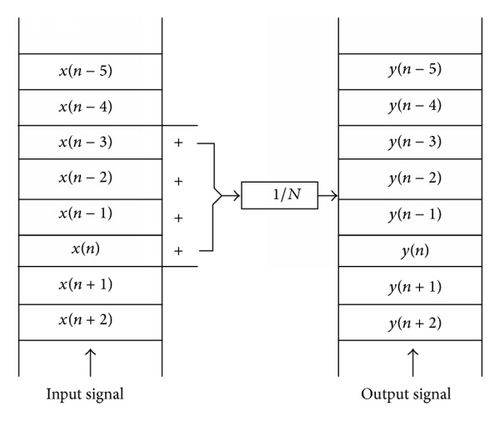
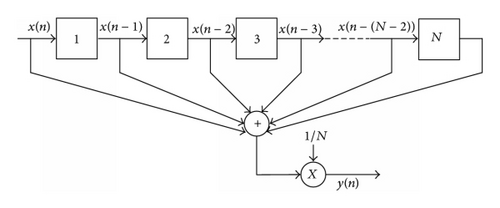
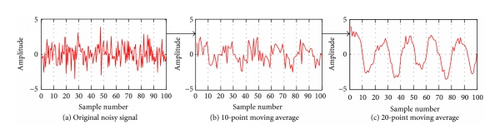
In Figure 5 an output signal of SMA is given where fluctuated (noisy) signal is smoothed by following (6), with 10 and 20 data points, where it can be observed that as the filter length increases (the parameter N) the smoothness of the output increases.
4. Case Example
Roof top centralized PV system installed at Zhejiang University, Yuquan Campus, College of Electrical Engineering Building, is taken as an example as shown in Figure 6. In fact the installed PV system is regarded as a good one because of the same module and facing the sun in the same angle and direction. Therefore irradiation of these panels is supposed to be uniform. However, one should notice the chiller, water storage tank, and weather data collection unit cause shading effects on adjacent panels as in red circles it can be seen.

With reference to ZJU roof top PV system, a 3 KW system was designed by using a 37-watt PV module to quantify the analysis; PV panel specifications are shown in Table 1. Approximation is made such that the PV panel peak power reduction rate is directly proportional to shading effects. Therefore, irradiance is estimated as (1) normal PV panel: 1000 W/m2 and (2) shaded PV panel between 768.36 W/m2 and 426.96 W/m2 as shown in Figures 7(a) and 7(b).
| Description | Rating |
|---|---|
| Maximum power (Pmax) | 37.08 Wp |
| Voltage at maximum power (Vmp) | 16.56 V |
| Current at maximum power (Imp) | 2.25 A |
| Open circuit voltage (Voc) | 21.24 V |
| Short circuit current (Isc) | 2.55 A |
| Total number of cells in series (Ns) | 36 |
| Total number of cells in parallel (Np) | 1 |
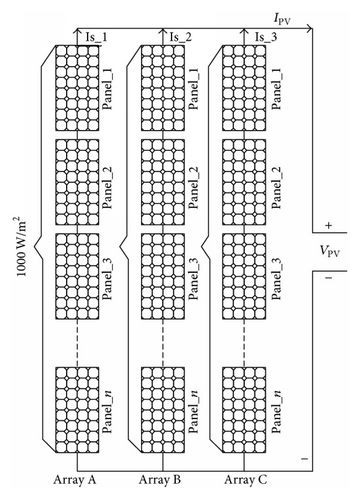
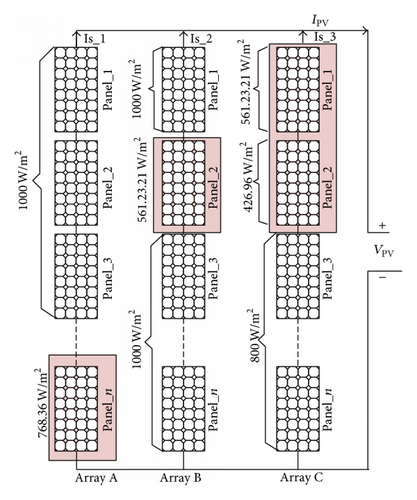
According to Figures 7(a) and 7(b), arrays A, B, and C with different irradiance IV-PV characteristic curves are drawn in Figure 8 in which multiple maximum power points due to irradiance mismatch are observed.
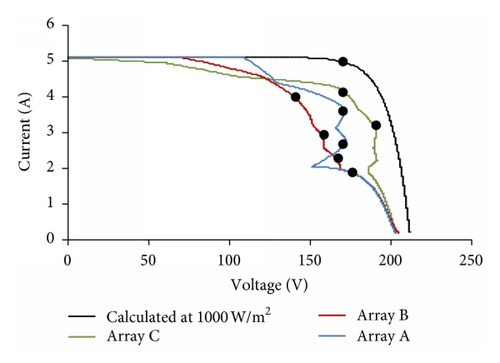
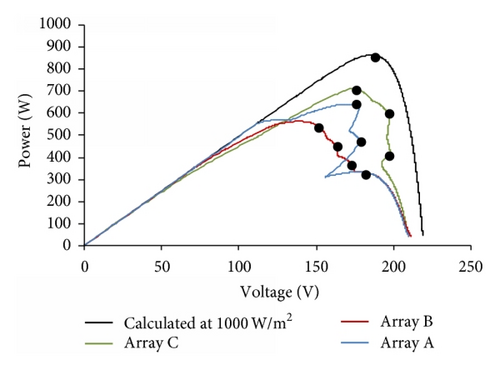
5. Results and Discussions
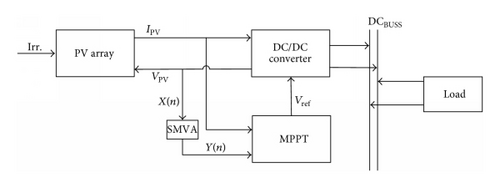
To validate the performance of proposed simple moving voltage average (SMVA) technique under nonuniform solar irradiation, a MATLAB/Simulink model was developed as shown in Figure 9, consisting of 3 KW PV array, a DC-DC boost converter (in Table 2 its component values are given), and a fixed step direct control incremental conductance MPPT controller with the SMVA technique.
| Component | Value | Unit |
|---|---|---|
| Capacitor (C) | 93.75 | uF |
| Inductor (L) | 1.66 | mH |
| Resistor (R) | 53.3 | Ohm |
| Rated input voltage | 200 | VDC |
| Rated output voltage | 400 | VDC |
| Rated output power | 3 | KW |
| Maximum average DC current | 7.5 | Amps |
| Switching frequency | 16 | KHz |
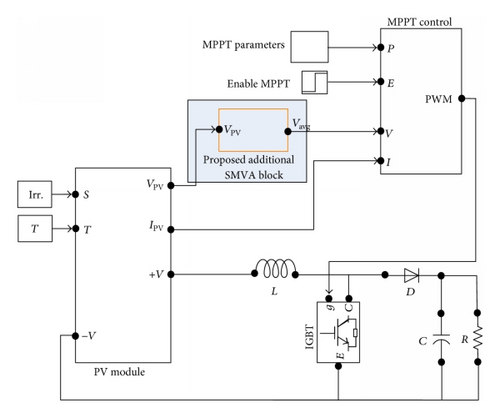
At the first step of the simulation, a nonuniform solar irradiation is applied to the PV array where irradiation was set to 800 W/m2 at t = 0.0 s and decreased to 600 W/m2 at 0.02 s and increased back to 1000 W/m2 at t = 0.04 s; finally the irradiation decreased from 800 W/m2 to 600 W/m2 from 0.06 s to 0.1 s, with 25°C constant temperature. In traditional PV systems photovoltaic voltage VPV is directly given as an input to MPPT controller but in the proposed model VPV is given as an input to the SMVA module as depicted in Figure 9, and output of SMVA is given as an input to MPPT controller. To investigate and validate the efficacy of the SMVA model buffer sizes (number of sample points) of N = 10 and N = 30 with a change in duty cycle Δd = 0.001 are applied; simulation results are presented in Figure 10.
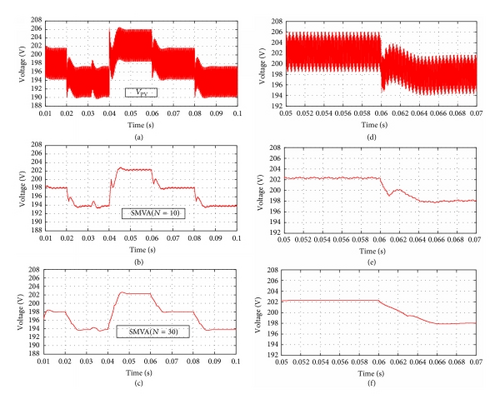
Figure 10(a) is an output voltage (VPV) of the PV array which is given as an input to the SMVA module to perform voltage smoothing and reduce the fluctuation using a span of data points following (6) with the buffer sizes N = 10 and N = 30. Figures 10(b) and 10(c) reveal the output comparison differences of fluctuated VPV and smoothed output of the proposed SMVA technique; Figures 10(d), 10(e), and 10(f) are zoomed from (a), (b), and (c) at t = 0.05 to t = 0.07 seconds where differences can be easily observed between (d), (e), and (f); results clearly indicate that the proposed method works effectively to reduce the fluctuation and improve the stability of voltage. It is observed in Figures 10(e) and 10(f) that a smaller buffer size produces higher fluctuation; as the buffer size increases, the fluctuation decreases.
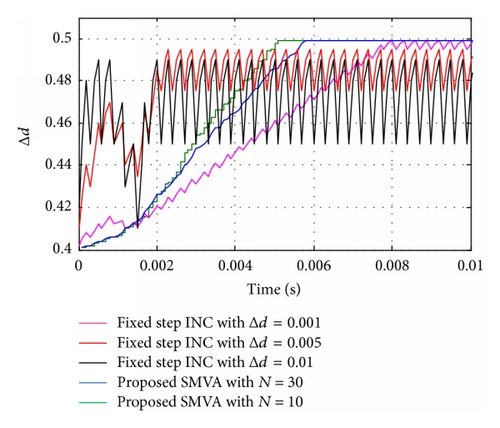
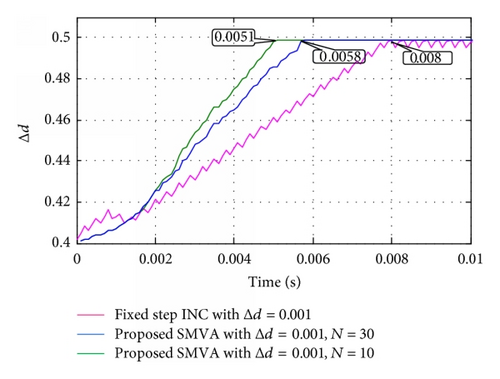
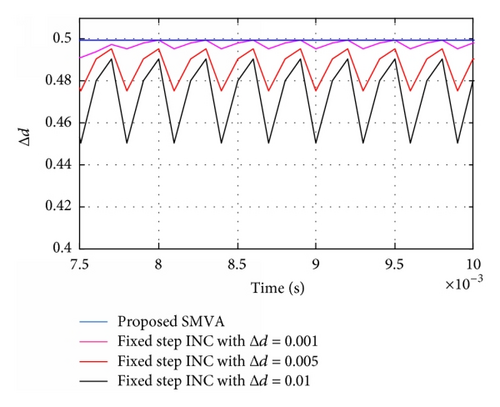
To demonstrate the effectiveness of the proposed SMVA model Figures 11(a), 11(b), and 11(c) show the variation of the duty cycle of fixed step direct control INC with Δd = 0.001, 0.005, and 0.01 and stability of the proposed SMVA model, where N = 10 and 30. In Figure 11(a), fixed step direct control INC and the proposed SMVA duty cycles with different Δd and N are depicted, whereas Figure 11(b) is exemplifying the maximum point (MP) tracking time (Ta), the fixed step INC reached MP at Ta = 0.008 seconds, and the proposed SMVA model gained the same MP at Ta = 0.0051 and Ta = 0.0058 seconds, respectively. Furthermore, Figure 11(c) is giving an idea about the stability of duty cycle at different Δd between INC and the proposed SMVA. The results clearly illustrate that performance of the proposed SMVA model is much better compared to the conventional fixed step INC with all the three step sizes Δd = 0.001, 0.005, and 0.01 during steady and dynamic state conditions and optimum duty cycle reached faster with less oscillation. The disadvantages of the fixed step INC with direct control are eliminated by the SMVA, in which the change in duty cycle Δd became stable because of extremely small |dP/dV| around MP, according to the change in the error absolute value between the instantaneous conductance and the incremental conductance.
Furthermore, to inspect the effectiveness of the proposed technique under nonuniform solar irradiation, different scenarios were simulated with a change in duty cycle Δd = 0.001, 0.005, and 0.01 and the SMVA buffer size number was adjusted at N = 10. Results are shown in Figures 12 and 13, where magenta color is representing the simple fixed step direct control INC’s output voltage and power and blue lines are for the proposed SMVA outputs. Results are showing that performance of the proposed technique is much better than that of fixed step direct control incremental conductance method at different duty cycle Δd step changes. It can be easily observed that the output voltage and power of the proposed technique give greater efficiency with more stability at all the different step size changes as compared to direct control INC, as it can be seen in Figures 12(a), 12(b), and 12(c) as Δd increases from 0.001 to 0.01, and INC’s output voltage decreases from the range of 385–407 volts to 374–397, where the upper limit decreases to 10 volts and the lower limit went down to 11 volts. In the SMVA output voltage remains higher than the INC’s within the range of 387–410 volts to 385–405 with the change in upper limit of 5 volts and lower limit to 2 volts. In the same way, in Figures 13(a), 13(b), and 13(c) output power comparisons between INC and the proposed SMVA method can be observed at Δd = 0.001, and INC’s output power is between 2775 and 3100 watts. At the same duty cycle SMVA output power is 2825–3150 watts and at Δd = 0.01 INC’s output power is 2625–2955, whereas SMVA output power is 2750–3055 watts.
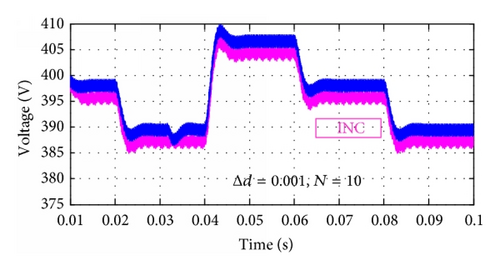
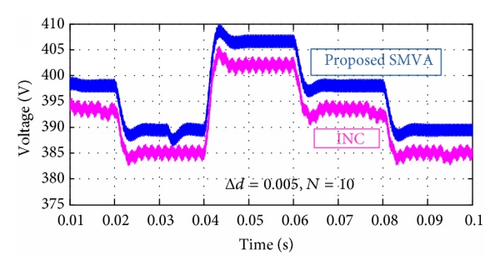
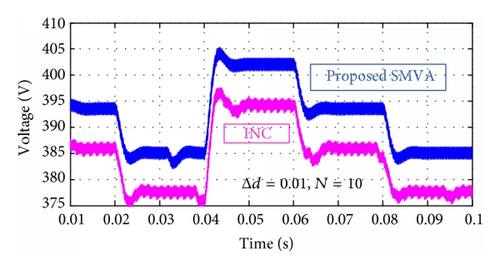
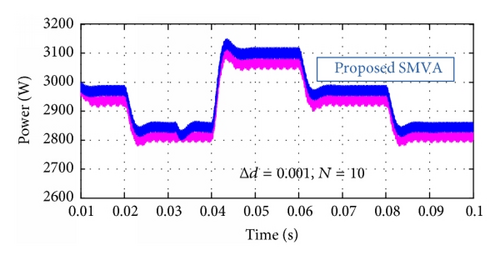
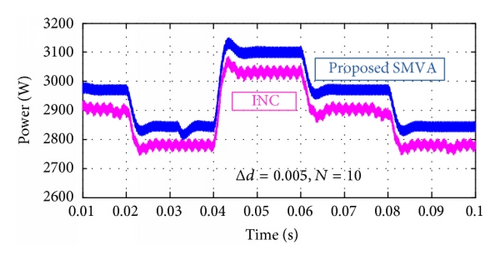
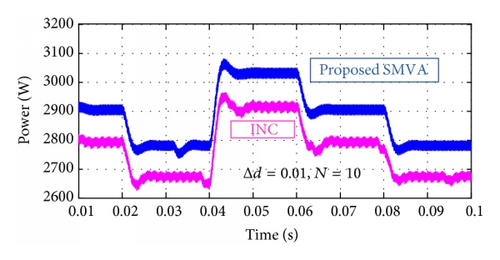
Figures 12 and 13 show that the proposed simple moving voltage average (SMVA) technique with direct control incremental conductance MPPT method can efficiently deal with the tradeoff between dynamic response speed and steady state accuracy. The steady state oscillations are almost eliminated because of extremely small |dP/dV| around MPP, as shown in Figure 10(f), the ripple voltage is less than 1.0 volt. The dynamic performance is obviously better than that with fixed step direct control INC.
Furthermore, Tables 3(a) and 3(b) surmise the measurement output voltage and power of INC and the proposed SMVA method with different buffer sizes N = 10, 30, and 50 and change in duty cycle Δd = 0.001, 0.003, 0.005, and 0.01 in order to verify the repeatability of the results, where the same tests were carried out at three different irradiance levels. It can be seen that, at Δd = 0.001, INC and SMVA perform extremely close in most cases because of small change in duty cycle, as it is reported in [31, 32] that smaller Δd reduces the steady state losses caused by the oscillation of the PV operating point around the MPP, but it makes the algorithm slower and less efficient in the case of rapid change in solar irradiation and larger step size contributes to faster dynamics but excessive steady state oscillations, resulting in a comparatively low efficiency as it can easily be seen in Figures 12 and 13 and Tables 3(a) and 3(b) as change in duty cycle increases from Δd = 0.001 to 0.01, INC’s output voltage and power decrease, and fluctuation increases. From the above study, it is observed that in most cases SMVA gives better results with more stability as compared to traditional fixed step direct control INC with faster tracking system under extreme weather conditions along with reduction in sustained oscillations, which verify that the proposed method is suitable for standalone PV system under extreme weather conditions not only in terms of bus voltage stability but also in overall system efficiency.
| Δd | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.001 | 0.003 | 0.005 | 0.01 | |||||||||||||
| INC | SMVA (N =) | INC | SMVA (N =) | INC | SMVA (N =) | INC | SMVA (N =) | |||||||||
| Irr. (W/m2) | 10 | 30 | 50 | 10 | 30 | 50 | 10 | 30 | 50 | 10 | 30 | 50 | ||||
| 600 | 388.4 | 390.4 | 390.6 | 390.3 | 386.3 | 390.6 | 390.6 | 390.6 | 383.1 | 386.1 | 386.2 | 386.2 | 378.5 | 386.1 | 386.1 | 386.1 |
| 800 | 396.8 | 398.5 | 398.7 | 399.1 | 394.8 | 399.0 | 399.0 | 399.0 | 391.5 | 394.7 | 394.6 | 394.6 | 386.7 | 394.6 | 394.6 | 394.6 |
| 1000 | 404.9 | 407.8 | 407.8 | 407.8 | 402.9 | 407.7 | 407.7 | 407.8 | 399.4 | 403.1 | 403.1 | 43.1 | 395.7 | 403.1 | 403.1 | 403.1 |
| Δd | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.001 | 0.003 | 0.005 | 0.01 | |||||||||||||
| INC | SMVA (N =) | INC | SMVA (N =) | INC | SMVA (N =) | INC | SMVA (N =) | |||||||||
| Irr. (W/m2) | 10 | 30 | 50 | 10 | 30 | 50 | 10 | 30 | 50 | 10 | 30 | 50 | ||||
| 600 | 2827 | 2861 | 2861 | 2861 | 2798 | 2861 | 2861 | 2861 | 2751 | 2795 | 2795 | 2795 | 2687 | 2795 | 2795 | 2795 |
| 800 | 2953 | 2986 | 2986 | 2986 | 2922 | 2988 | 2988 | 2988 | 2874 | 2919 | 2919 | 2919 | 2804 | 2919 | 2919 | 2919 |
| 1000 | 3081 | 3118 | 3118 | 3118 | 3039 | 3118 | 3118 | 3118 | 2992 | 3047 | 3047 | 3047 | 2931 | 3047 | 3047 | 3047 |
6. Conclusion
In this paper, simple moving voltage average (SMVA) technique with fixed step direct control incremental conductance method was employed. Simulation results show that proposed technique is able to reduce VPV oscillations, thereby reducing the power losses faced by the conventional INC algorithm under nonuniform solar irradiation. Also this method is able to improve not only the steady and dynamic state but also the design efficiency of system. In conclusion the proposed method performs accurately and better than the conventional INC algorithm and simulation results verify the feasibility and effectiveness of the proposed method.
Conflict of Interests
The authors declare that there is no conflict of interests regarding the publication of this paper.
Acknowledgments
This work is sponsored by the National Nature Science Foundations of China (51490682, 51377112) and the Zhejiang Provincial Natural Science Foundation (LR16E070001).




