In this paper tunnel probabilistic structural analysis (TuPSA) was performed using the first order reliability method (FORM). In TuPSA, a tunnel performance function is defined according to the boundary between the structural stability and instability. Then the performance function is transformed from original space into the standard normal variable space to obtain the design point, reliability index, and also the probability of tunnel failure. In this method, it is possible to consider the design factors as the dependent or independent random parameters with arbitrary probability distributions. A software code is developed to perform the tunnel probabilistic structural analysis (TuPSA) using the FORM. For validation and verification of TuPSA, a typical tunnel example with random joints orientations as well as mechanical properties has been studied. The results of TuPSA were compared with those obtained from Monte-Carlo simulation. The results show, in spite of deterministic analysis which indicates that the rock blocks are stable, that TuPSA resulted in key-blocks failure with certain probabilities. Comparison between probabilistic and deterministic analyses results indicates that probabilistic results, including the design point and probability of failure, are more rational than deterministic factor of safety.

1. Introduction

Structural instability is the most dominant failure mechanism of underground openings in moderately jointed rock masses. Traditional analyses in such openings have been largely based on rock mass classification methods. Rock load [1], RQD [2], RSR [3], RMR [4], and rock tunneling quality index (Q) [5] are the most practical rock mass classifications. Despite the empirical effectiveness of these classifications, they largely ignored particular stability problem due to the formation of removable rock blocks around the tunnel walls.

Block instability is not necessarily dependent on any rock mass classifications. Block theory [6] provides a mathematical and geometrical procedure to define the stability of rock structures triggered by discontinuities geometry. For a number of joint intersections behind an excavation free face, block theory determines the combinations of joints half spaces which create a removable rock block, block geometry, probable sliding or falling direction, and the safety factor of block using a rigorous approach. Block theory method considers the rock mass and support properties as deterministic parameters. However, they improved our understanding of structural instability of tunnels, in spite of their assumptions, most of the geomechanical characteristics of rock masses such as discontinuities orientation and mechanical properties and also support properties vary in wide ranges.

Unlike the probabilistic stress-controlled instability analysis, few researches have been performed on probabilistic instability analysis of block failures in underground openings: [7–9]. On the other hand, in these cases, the analysis is limited to the specific case studies with limited random dimension or specific probability distributions. So far, there is no direct study on the probabilistic analysis of structural instability in underground openings. Therefore, in this research a tunnel probabilistic structural stability analysis (TuPSA) was developed using first order reliability method.

For this purpose, at first, the reliability problem and first order reliability method (FORM) are explained, and then the performance function for tunnel structural stability is presented. By combining these two definitions, tunnel probabilistic structural stability analysis (TuPSA) will be explained. A computer code is developed for reliability analysis of structural failures and performing the TuPSA method. The reliability problem of a typical tunnel example is solved by developing computer code assuming different scenarios. Finally, the results are compared to those obtained from Monte-Carlo simulations.

2. First Order Reliability Method (FORM)

For a tunnel system, reliability could be defined as the ability of the tunnel or its components to perform the required functions under the specific uncertain conditions. A random uncertain parameters vector such as (x₁, x₂, …, x_n), which could include rock material, support, and joints geometrical parameters, follows a multivariate probability density function f(x₁, x₂, …, x_n). For a specific designed tunnel system, there is a performance function P(x₁, x₂, …, x_n) that is defined to be zero at a limit state, less than zero at system failure domain, and greater than zero for safe state. The objective of reliability analysis is to calculate the probability of failure which can be expressed as [10, 11]

()

where p_f is failure probability and (x₁, x₂, …, x_n) is uncertain parameters vector. The concepts of performance limit state, failure and safe regions, and probability of failure (domain of integration that is illustrated by shaded region) are illustrated in Figure 1. In Figure 1, shaded area indicates the failure domain and dashed lines are the contours that indicate the probability distributions of two variables (for sake of simplicity).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

General reliability problem for two probabilistic variables [10].

The general solution to (1) is the Monte-Carlo simulation that relies on repeated random sampling based on the multivariable density function to compute their performance results. The probability of failure is estimated from the ratio of number of failed cases, n_f, per total number of simulation iterations, n, as follows:

()

The sample size (n) must ensure coefficient of variation of calculated p_f,

, becomes reasonably small. Coefficient of variation of p_f is estimated using the following equation [12]:

()

The analytical solution of (1) is not available, unless the multivariable density function is normal and the performance function is linear or quadratic [10]. These conditions led to the idea of FORM solution. In FORM solution, by replacing the physical nonnormal random variables, (x₁, x₂, …, x_n), with the standard normal random variables (uncorrelated Gaussian random variables with zero mean and unit standard deviation), the performance function is transmitted to standard normal space spanned by standard normal variables (z₁, z₂, …, z_n) (Figure 2).

Most likely failure point in standard space is called the design point or β-point (Z^∗ in Figure 2). By replacement of the actual limit state (P = 0) with the approximate linear limit state function at design point (P_L = 0), the probability of failure could be approximated by [11]

()

Here, β is the distance between origin and design point in normal space and Φ is the cumulative density function (CDF) of standard normal variables. Using this transformation, the multiple integration of (1) reduces to a constrained nonlinear optimization problem as

()

where Z = (z₁, z₂, …, z_n) is the vector of standard normal random variables, Z^T is the transpose of Z, X = (x₁, x₂, …, x_n) is the physical nonnormal random variables vector, and g is the translation function used to convert the standard normal vector to the physical variables vector. For the noncorrelated and correlated physical variables, translation function can be defined as (6) [13] and (7), respectively:

()

Each nonnormal component, x_i, can follow any arbitrary cumulative distribution function, F_i, and L is the Cholesky factor of correlation coefficients matrix of random variables, C, [10]. Cholesky factor can be determined using the following relation:

()

Here, C is the correlation coefficients matrix of physical random variables and L^T is the transpose matrix of L. The first order reliability method (FORM) could be performed on the systems with known performance function and specific random parameters by using (4)–(8).

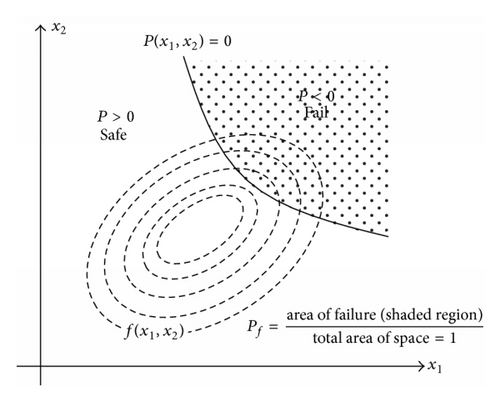
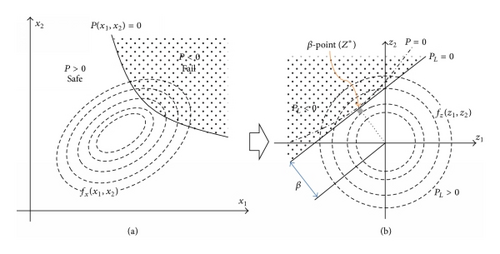
3. Tunnel Probabilistic Structural Stability Analysis (TuPSA)

In TuPSA method, by defining the tunnel performance function, it is possible to perform the FORM analysis using (4)–(8). Definition of tunnel structural performance function is one of the most important stages in TuPSA which is determined by the goals of tunnel design. The goal of geomechanical designs in dealing with structural instabilities is to prevent the blocks and wedges from sliding and falling into the underground opening. Therefore, the performance function is defined as follows:

()

It is difficult to develop an analytical performance function which includes all (most important) design factors, but it is possible by using the nested functions. Details of the performance function calculation, used in this paper, are presented here. The main assumptions of TuPSA are as follows:

(i)
The blocks formed around the tunnel have maximum possible volume (considering the key blocks).
(ii)
Specific falling/sliding blocks have no influence on other blocks’ stability.
(iii)
Bolts are considered as the simple forces applied to the blocks in specific directions.
(iv)
The influence of field stress on blocks stability [14] is not considered.
(v)
The distribution of uncertain parameters is available.

Many parameters are influencing the tunnel structural instabilities. The main parameters governing the overall stability of opening and their symbols used in analysis are as follows:

(1)
geometrical parameters:
- (a)
  tunnel axis orientation: trend and plunge, TO,
- (b)
  tunnel radius, r,
- (c)
  joints orientation: joints dip and dip direction, JD,
(2)
mechanical parameters:
- (d)
  cohesion of joints, C_j,
- (e)
  friction angle of joints, φ_j,
- (f)
  tensile strength of joints, Ten,
- (g)
  water pressure on joints face, u,
- (h)
  unit weight of rock mass, γ,
- (i)
  unit weight of shotcrete, γ_s,
- (j)
  shotcrete thickness, t,
- (k)
  shotcrete shear strength, τ_s,
- (l)
  bolts force pattern around the tunnel, F_b,
- (m)
  seismic coefficient, K,
- (n)
  seismic force direction, Sd.

There are different consecutive stages to define the tunnel structural performance function. Some of these stages deal with the geometry of blocks and other ones deal with the limit-equilibrium analysis. Different software codes have been developed to compute these functions. By combining these codes using the procedure presented in Figure 3, the performance function for tunnel structural stability has been achieved. Some of these stages, which are used in this research, are presented here briefly and in the functional form.

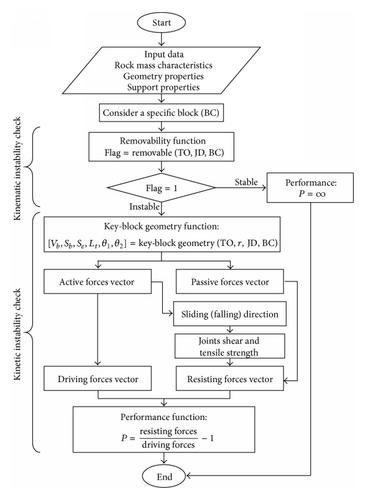
3.1. Removability Function

For 3 joint sets, considering all combinations of joints half spaces, there are eight tetrahedral block types codified 000, 001, 010, 011, 100, 101, 110, and 111. A 0 in the ith place signifies that spherical triangle belongs to the upper half-space of ith joint plane and conversely a 1 signifies that spherical triangle belongs to the lower half-space of ith joint plane. As defined by Figure 3, by checking the kinematic instability of a block combined from joints half spaces, the removability of block is determined (from a geometrical point of view) based on block theory method (BTM). The inputs of this function are joints and tunnel axis orientations and also the code indicating the block and the binary output indicates the removability of the block:

()

where Flag is a binary 0 or 1 that indicates the removability of the block (0: not removable, 1: removable) and BC is the block code.

3.2. Key-Block Geometry Function

By determining the removable blocks with kinematic analysis, it is possible to check the kinetic instability of these blocks (Figure 3). At first, the geometry of biggest/critical blocks (key blocks) around the tunnel is determined based on BTM. Key-block geometry function determines the key-block volume, V_b, block face area, S_b, excavation face area of the block, S_e, trace length of joints in excavation rim, L_t, and angular intervals of block outcrops in the tunnel, θ₁ and θ₂ (Figure 4). The key-block geometry function could be presented by

()

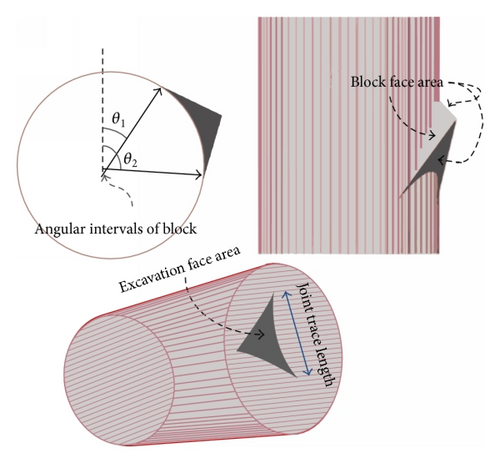
3.3. Factor of Safety Function

By defining a specific key-block geometry, it is possible to calculate the active and passive force vectors (in global ENU coordinate system) acting on the key block. In this study, the resultant active and passive force vectors are obtained from (12) and (13), respectively [15, 16]:

()

where A is active force vector, W is block weight vector, C is shotcrete weight vector, U is water force vector, E is seismic force vector, F_p is passive force vector, H is shotcrete shear resistance force vector, and B is bolt force vector.

The probable sliding direction is computed by considering active forces (A vector). By knowing the sliding direction, it is possible to calculate the joints shear and tension strength using one of the joint behavior models such as Mohr-Coulomb model (Figure 3). Finally, a limit equilibrium analysis is performed to calculate the safety factor. The general formulation is as follows:

()

In this study the performance function of each key block has been defined by block factor of safety as follows:

()

The reliability problem of structural stability has been defined by placing of tunnel performance function (15) in general FORM problem (5). To solve resulting problem, a computer code has been developed. Due to high complexity of the tunnel performance function, it is impossible to introduce an analytical and or a closed form solution for the resulted optimization problem. To overcome this issue, a numerical optimization method based on “interior-point algorithm’’ [17] has been used. The optimization problem was solved using TuPSA code for a typical example which is presented in this work. The results show the great capability of FORM method to reliability analysis of structural instability with low failure probability instead of Monte-Carlo simulation.

4. Typical Example

Deterministic and probabilistic properties of a circular tunnel and surrounding rock mass are given in Table 1. Clear correlations are observed between joints mechanical properties as well as joints geometrical parameters. Correlation coefficient matrix of random parameters is illustrated in Table 2. The stability of the tunnel has been studied by considering 5 different scenarios from deterministic to fully probabilistic analysis. These scenarios are as follows:

(S1)
The parameters variability has no influence on the stability and only the mean values are effective in analysis. A deterministic safety factor and block performance were determined using the algorithm presented in Figure 3.
(S2)
Only the joints strength parameters (C, φ, Ten) variability has an influence on the stability and these parameters are assumed as the independent variables.
(S3)
It is similar to scenario 2, but with considering the effects of correlations between random variables.
(S4)
Only the joints orientation parameters (DD₁, D₁, DD₂, D₂, DD₃, D₃) variability has an influence on the stability and these parameters are assumed as the correlated random variables.
(S5)
All the joints properties (mechanical and geometrical properties) variability has an influence on the stability and these parameters are assumed as correlated random variables.

Here, the reliability analysis steps for the general case (scenario 5) are expressed. The other solutions are simply derived from this case.

(1)
Determine physical random vector using the standard normal variables.
Consider X = (C, φ, Ten, DD₁, D₁, DD₂, D₂, DD₃, D₃) as the physical random variables vector and Z = (z₁, z₂, …, z₉) as the standard normal variables vector. The following steps are used to determine the translation function (X = g(Z) in (5)):
- (a)
  Define the Cholesky factor of correlation matrix based on (8):
  ()
- (b)
  Transform standard normal vector to the correlated normal vector:
  ()
- (c)
  Transform correlated normal variables to the physical random variables based on (7):
  ()
(2)
Solve the nonlinear optimization problem of (5) by using the TuPSA computer code.

Table 1. Properties of the circular tunnel.

Deterministic parameters		Probabilistic parameters
Parameter	Value	Parameter	Distribution
TTP	0°, 0°	/°	Normal (μ = 30, σ = 5)
r	2.5 m	/°	Normal (μ = 25, σ = 3)
u	0 KPa	D₂/°	Normal (μ = 55, σ = 7)
γ	2.7	DD₂/°	Normal (μ = 110, σ = 5)
K	0	D₃/°	Normal (μ = 70, σ = 4)
Support	No support	DD₃/°	Normal (μ = 240, σ = 7)
		C/KPa	Truncated normal (μ = 20, σ = 11) ≥0
		φ/°	Log-normal (μ = 30, CoV = 0.07)
		Ten/KPa	Uniform ([0–8])

^∗D_i: dip of ith joint set; ^∗∗DD_i: dip direction of ith joint set.

Table 2. Correlation coefficient matrix of random parameters.

Variable	C	φ	Ten	DD₁	D₁	DD₂	D₂	DD₃	D₃
C	1	−0.5	+0.8
φ	−0.5	1	−0.3	0
Ten	+0.8	−0.3	1
DD₁				1	0.93	0.5	−0.4	−0.4	−0.07
D₁				0.93	1	0.45	−0.3	−0.3	−0.1
DD₂		0		0.5	0.45	1	−0.7	−0.5	−0.1
D₂		0		−0.4	−0.3	−0.7	1	0.3	0.2
DD₃				−0.4	−0.3	−0.5	0.3	1	0.2
D₃				−0.07	−0.1	−0.1	0.2	0.2	1

5. Results and Discussion

By deterministic stability analysis using the mean values of joints properties (scenario 1), six removable blocks have been found and analyzed using the kinematic and kinetic instability analysis. The position of these blocks around the circular tunnel has been illustrated in Figure 5. The performance function determination algorithm which is illustrated in Figure 3 has been used in this analysis. The results of key blocks removability, geometry, safety factor, and performance are presented in Table 3.

Table 3. Results of deterministic analysis considering the mean values of random parameters (scenario 1).

Block code (BC)	Key-block geometry				F_S	Performance (P)
Block code (BC)	Volume (vb) m³	Joints area (S_b) m²	Excavation face area (S_e) m²	Joints trace length (L_t) m	F_S	Performance (P)
0 0 0/UUU	0.1906	0.9486 0.6044 0.5544	1.3972	3.3441 2.3024 3.0437	∞ (stable)	∞

0 0 1/UUL ^∗	0.0098	0.0630 0.2109 0.0650	0.2768	1.0916 1.7541 1.3197	47.08	46.08

0 1 0/ULU	0.6032	1.1896 1.3302 1.9408	2.5946	3.8899 3.5865 4.3141	18.33	17.33

1 0 1/LUL	0.6032	1.1896 1.3302 1.9408	2.5946	3.8899 3.5865 4.3141	3.05	2.05

1 1 0/LLU	0.0098	0.0630 0.2109 0.0650	0.2768	1.0916 1.7541 1.3197	8.97	7.97

1 1 1/LLL	0.1906	0.9486 0.6044 0.5544	1.3972	3.3441 2.3024 3.0437	1.05	0.05

^∗UUL: key block created by combination of 1st and 2nd joints upper half spaces and 3rd joint lower half space (based on BTM; see [6]).

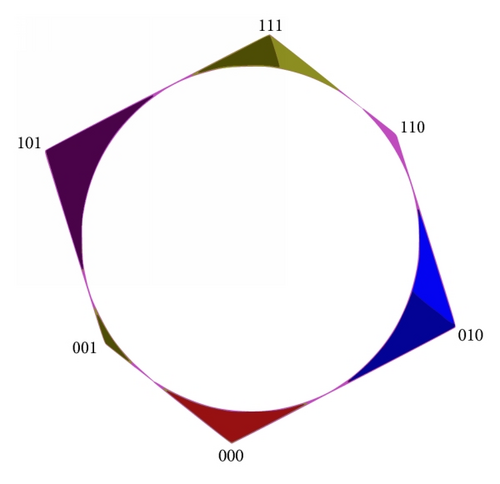
The probabilistic analysis using the TuPSA method has been carried out for scenarios 2–5 and the results are presented in Figures 6 and 7. Figure 6 illustrates the reliability index of each key block for different scenarios. Figure 7 illustrates the probability of each block failure for different scenarios. Note that the small probability of failures is illustrated in logarithmic scale. For validation, a Monte-Carlo simulation has been carried out for scenario 2. In the Monte-Carlo simulation, the number of iterations is selected so that, based on (3), the coefficient of variation of p_f () becomes less than 0.1. A comparison between results of TuPSA method and Monte-Carlo simulation for scenario 2 is presented in Table 4.

Table 4. Results of the reliability analysis of tunnel stability, considering the joints strength parameters (C, φ, Ten) as the independent random variables (scenario 2).

Block code (BC)	FORM analysis				Monte-Carlo simulation
Block code (BC)	Reliability index (β)	Probability of failure (p_f) %	Calculation time (sec) ^∗	Function iterations	Iterations (~needed)	Probability of failure (p_f) %	Simulation time (sec) ^∗ (~needed)	Actual
0 0 0	—	—	—	—	—	—	—	—
0 0 1	3.838	6.19 × 10⁻³	10.6	58	~1.62 × 10⁶	N-A ^∗∗	~2.82 × 10⁵	N-A
0 1 0	10.320	2.76 × 10⁻²³	9.4	57	~6.61 × 10²⁶	N-A	~1.15 × 10²⁶	N-A
1 0 1	1.569	5.8	8.5	52	2000	5.5	348	0.093
1 1 0	2.021	2.17	9.7	52	5000	2.01	890	0.099
1 1 1	0.066	47.4	10.6	67	600	47.5	104.9	0.043

∗: calculation (simulation) time using a 2.67 GHz, core i5 processor.
∗∗: it is not possible to calculate in reasonable time period with ordinary processing units.

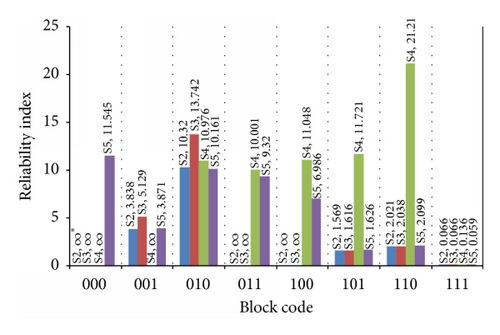
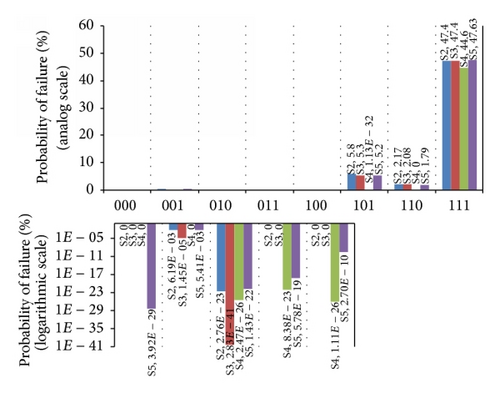
A comparison between reliability analysis using correlated and uncorrelated joint friction and cohesion strength (Figures 6-7) indicates that considering the negative correlation between joints friction and cohesion strength parameters reduces the probability of block failure and increases the tunnel reliability index.

As can be seen from Figures 6-7 (scenario 4), for the removable blocks with high safety factor (greater than 3), the variability of joints orientation has very little impact on the event of failure. By performing a comparison between scenarios 2, 3, and 4, it can be concluded that for these blocks the variability of strength parameters has a more effective role in failure events. By comparing scenarios 2, 3, and 4 for block [1 1 1], it can be concluded that, for the marginal blocks which have a low safety factor (between 1 and 2), both of the geometrical and strength variabilities are important, separately as well as together, in the failure event.

Table 4 illustrates the results of FORM analysis and the Monte-Carlo simulation for the assumed case study. Considering the running time and accuracy of results, it is clear that FORM is more efficient and more precise than ordinary Monte-Carlo simulation (in finite iterations). This fact is more evident when the probability of failure is too small and consequently it requires too many simulation iterations to evaluate accurate probability based on (3). Table 4 illustrates that, on the contrary to FORM analysis, the simulation iterations and simulation time increase when the probability of failure decreases.

6. Conclusions

A reliability-based design methodology for tunnel structural instability (TuPSA) is developed. Many sources of uncertainties can be modeled and analyzed in evaluating the probabilistic tunnel stability. The physical random variables are considered to have arbitrary probability distribution with any types of correlations. A combination of tunnel structural stability models and first order reliability method (FORM) has been used for reliability analysis of structural instabilities around the circular tunnels. In this method, by transforming the performance functions from the space spanned by physical random variables into the noncorrelated standard normal random variables space, the reliability index and probability of failure are calculated via optimization techniques.

A case study with five scenarios from deterministic to full probabilistic state is presented to show the implementation of the TuPSA model and to obtain an estimate of the target β-value for each removable key block. It is possible to replace factor of safety with the performance of tunnel considering the tunnel design goals. Comparison between probabilistic and deterministic analyses results indicates that probabilistic results, including the design point and probability of failure, are more rational than deterministic factor of safety. Comparison between the failure probabilities obtained from FORM and those obtained from Monte-Carlo simulations indicates that FORM is the most efficient reliability method and its accuracy is very high and more than sufficient.

Deterministic methods are the base of design and analysis in rock engineering. However, the reliability analysis presented in this paper demonstrates the applicability of the statistical and probabilistic analysis in problems dealing with uncertainties and variability. However reliability analysis could consider the effects of uncertainties in stability analysis, faced with the same problem as the deterministic approaches. Both of the deterministic and probabilistic analyses use the same failure models that may have inherent weaknesses.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

References

1 Terzaghi K., Rock Defects and Loads on Tunnel Supports, 1946, Graduate School of Engineering, Harvard University.
Google Scholar
2 Deer D. U., Technical description of rock cores for engineering purpose, Rock Mechanics and Rock Engineering. (1964) 1, 17–22.
Google Scholar
3 Wickham G., Tiedemann H., and Skinner E. H., Support determinations based on geologic predictions, Proceedings of the North American Rapid Excavation & Tunneling Conference, 1972, 43–64.
Google Scholar
4 Bieniawski Z. T., Engineering Rock Mass Classifications: A Complete Manual for Engineers and Geologists in Mining, Civil, and Petroleum Engineering, 1989, John Wiley & Sons.
Web of Science® Google Scholar
5 Barton N., Lien R., and Lunde J., Engineering classification of rock masses for the design of tunnel support, Rock Mechanics Felsmechanik Mécanique des Roches. (1974) 6, no. 4, 189–236, https://doi.org/10.1007/bf01239496, 2-s2.0-0016313398.
10.1007/BF01239496
Google Scholar
6 Goodman R. E. and Shi G., Block Theory and Its Application to Rock Engineering, 1985, Prentice-Hall.
Google Scholar
7 Chen G., Probabilistic key block analysis of a mine ventilation shaft stability—a case study, Geomechanics and Geoengineering. (2012) 7, no. 4, 255–262, https://doi.org/10.1080/17486025.2011.592609, 2-s2.0-84869381381.
10.1080/17486025.2011.592609
Google Scholar
8 Li D., Zhou C., Lu W., and Jiang Q., A system reliability approach for evaluating stability of rock wedges with correlated failure modes, Computers and Geotechnics. (2009) 36, no. 8, 1298–1307, https://doi.org/10.1016/j.compgeo.2009.05.013, 2-s2.0-70349444957.
10.1016/j.compgeo.2009.05.013
Web of Science® Google Scholar
9 Low B. K. and Einstein H. H., Reliability analysis of roof wedges and rockbolt forces in tunnels, Tunnelling and Underground Space Technology. (2013) 38, 1–10, https://doi.org/10.1016/j.tust.2013.04.006, 2-s2.0-84878794027.
10.1016/j.tust.2013.04.006
Web of Science® Google Scholar
10 Phoon K. K., Reliability-Based Design in Geotechnical Engineering: Computations and Applications, 2008, Taylor & Francis.
10.1201/9781482265811
Google Scholar
11 Hasofer A. M. and Lind N. C., An Exact and Invariant First-Order Reliability Format, 1973, Solid Mechanics Division, University of Waterloo.
Google Scholar
12 Shooman M. L., Probabilistic Reliability: An Engineering Approach, 1968, McGraw-Hill, New York, NY, USA.
Web of Science® Google Scholar
13 Rubinstein R. Y., Simulation and the Monte Carlo Method, 1981, Wiley, New York, NY, USA.
10.1002/9780470316511
Google Scholar
14 Brady B. H. G. and Bray J. W., The boundary element method for determining stresses and displacements around long openings in a triaxial stress field, International Journal of Rock Mechanics and Mining Sciences and. (1978) 15, no. 1, 21–28, https://doi.org/10.1016/0148-9062(78)90718-0, 2-s2.0-0017934667.
10.1016/0148-9062(78)90718-0
Web of Science® Google Scholar
15 Rocscience, Unwedge Theory Manual—Factor of Safety Calculations, Rocscience Inc, http://www.rocscience.com/help/unwedge/webhelp/pdf_files/theory/unwedge_theory.pdf.
Google Scholar
16 Curran J. H., Corkum B., and Hammah R. E., Three-dimensional analysis of underground wedges under the influence of stresses, Proceedings of the Gulf Rocks Conference, June 2004, Elsevier Science, 449–466.
Google Scholar
17 Byrd R. H., Hribar M. E., and Nocedal J., An interior point algorithm for large-scale nonlinear programming, SIAM Journal on Optimization. (1999) 9, no. 4, 877–900, https://doi.org/10.1137/s1052623497325107, MR1724768, 2-s2.0-0033471382.
10.1137/S1052623497325107
Web of Science® Google Scholar

All articles

Tunnel Probabilistic Structural Analysis Using the FORM

Abstract

1. Introduction

2. First Order Reliability Method (FORM)