Solution of Turbine Blade Cascade Flow Using an Improved Panel Method

1. Introduction

The design of modern aeroengine gas turbine adopts various numerical methods to increase design efficiency. At the preliminary design stage, the major work for numerical method is repetitive calculations of flow fields over a wide range of blade geometries. This task has been dominated by field methods such as finite differential methods and finite element methods with the advent of computers. However, the use of these field methods requires an experienced user to generate a body-fitted mesh, which is labor intensive. On the other hand, panel method only requires boundary meshes that are one dimension lower than the flow field, reducing the work and difficulty for mesh generation enormously. This method is based on boundary integral equation: it formulated the flow about arbitrary configurations as integration of analytic solutions of singularity distribution over boundary surface [1]. It was initially developed for incompressible potential flow [2]. Soon, the implement of linearised potential equation endowed the method with the capability of solving subsonic and supersonic external flow [3]. Various panel methods were developed using different kind of singularities and higher order panel elements since then eventually evolved into series of computer codes commonly in industrial use [4–7].

The main drawback of the panel method is the limitation of its application to linear potential flow. To be specific, the flow should either be incompressible or possess a sole free stream as linearization reference. But modern aeroengine gas turbines generally work at high subsonic/transonic condition and adopt blades with large deflection, implying that (1) the incompressible assumption is not applicable and (2) the free streams upstream and downstream of the blades are quite different. There are two schemes to overcome this restriction: the field panel method that uses a field mesh to account for nonlinear effects [8] or the correction correlations that transform the incompressible solution to compressible solution. Since the aim of this paper is to develop a mesh-free method, the correction correlations are chosen as the scheme to be used.

There are several forms of corrections based on free stream Mach number [2]. Their combination with the panel method is straightforward and reliable [9]. But as mentioned before, the free stream Mach numbers upstream and downstream of aeroengine gas turbine blades are not the same. Lieblein and Stockman developed a correction for this circumstance [10], which is deduced from empirical observation on the compressible flow in a turbine nozzle passage. However, the error of this method is very large at high subsonic Mach number when compared with experiment data.

A method to rapidly calculate turbine blade cascade flow is presented in this paper. The flow field is solved with the panel method at first to obtain an incompressible solution. Then, the free stream velocities upstream and downstream are modified with a deviation angle model. The compressible solution is obtained by applying compressibility corrections at each cross section with local average Mach number on the cross section as a reference value. Examples are given to demonstrate the capabilities of the method.

2. Modeling Method

2.1. Panel Method

The flow through an infinite cascade is shown in Figure 1. The governing equations and boundary conditions for inviscid incompressible flow through an infinite cascade are as follows:

$$ ()

$$ ()

$$ ()

The solution is developed using a velocity potential that is the sum of a constant onset velocity potential plus a disturbance induced by the cascade. The quantities of both are unknown:

$$ ()

$$ ()

$$ ()

The onset velocity is constant, so (1), (5), and (6) yield

$$ ()

The flow field is determined by solving (1) subject to boundary conditions (2) and (3).

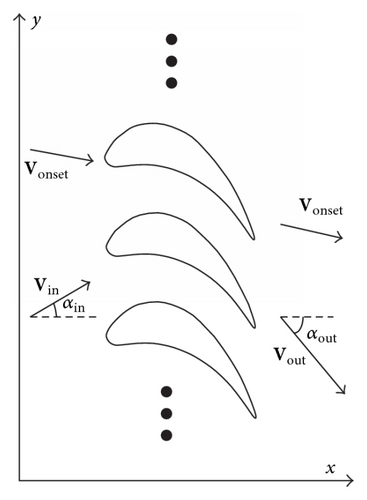
Laplace’s equation governs the disturbance potential (7). Since it is a linear equation, simpler solutions of Laplace’s equation may be added together to develop solutions with higher complexity. A general solution to flow over a body or cascade of bodies may be developed by using basic incompressible potential flow solutions for source and vortex flows distributed along the body surfaces and varying the strength of the source and vortex singularities so that the problem’s boundary conditions are satisfied.

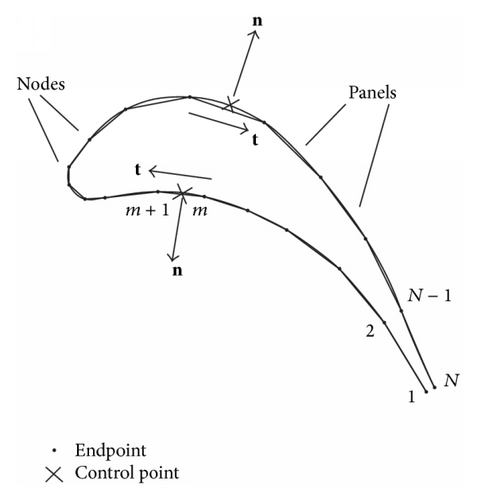
In this paper, the surface of the body is represented by inscribing a polygon as shown in Figure 2. Flat panel elements with constant source and vortex singularity strengths are used for simplicity. The source strength varies for each element, while the vortex strength is identical over the whole blade surface. A control point is selected on each element centroid where the normal velocity boundary condition is to be applied. There will be N element endpoints and N − 1 control points. All the endpoints are arranged clockwise. The trailing edge is left open to avoid a velocity peak in the inviscid calculation.

The variables n and t are the unit normal and tangent vectors of the local panel elements, respectively. The velocity in the flow field could be expressed in complex form as follows:

$$ ()

where σ_j is the source strength on the jth panel element and γ is the vortex strength over blade surface. A_j and B_j are complex influence factors of the source and vortex at the jth panel element. According to Hess and Smith [11], their expressions are

$$ ()

where z_j, z_j+1 are the endpoints of the jth element, β is the argument of dz = z_j+1 − z_j, ζ is the evaluated point, and pitch stands for the value of pitch.

Applying (2) at those control points would yield

$$ ()

Another boundary condition is the upstream boundary condition (3). For a nominalized velocity field, the inlet velocity could be expressed as follows:

$$ ()

If the circulation over the blade is Γ (the sum of the vortex strength over the blade), its equation is

$$ ()

where l_j is the length of the jth panel element. So the upstream boundary condition could be expressed as

$$ ()

For airfoil inviscid calculations, a Kutta condition must be applied at the trailing edge:

$$ ()

Equations (10), (13), and (14) compose a linear equation group that would yield the values of the singularity strength and V_onset, from which the velocity at any position can be obtained by (8).

2.2. Compressibility Correction

Lieblein’s correction for internal flow is based on the flow status of each cross section:

$$ ()

Lieblein’s formula was derived from empirical observation over a turbine nozzle [10]. As shown later in the paper, this does not match with experimental data well. However, this formula indicates the importance of considering the status of local flow paths in the compressibility correction correlations. Thus, a new compressibility correction is developed in this paper: a reference Mach number at the evaluated cross section is calculated first and then is used to transform the local incompressible solution into a compressible solution using the formula for small disturbance flow, such as Karman-Tsien formula:

$$ ()

Assume there is a virtual flow path where the blade thickness is neglected, and the mass flow rate and average flow angle are equal to those of real blades, as shown in Figure 3 with dash-dotted line. SP is the cross section in the flow path where the compressibility correction to be applied, S^′P^′, is the cross section of that virtual flow path at the same axial location. α_ref and M_ref are the average flow angle and the average Mach numbers at S^′P^′. According to mass conservation, there is

$$ ()

When M_ref is calculated using (17), (16) may be used to transform incompressible solutions into compressible solutions.

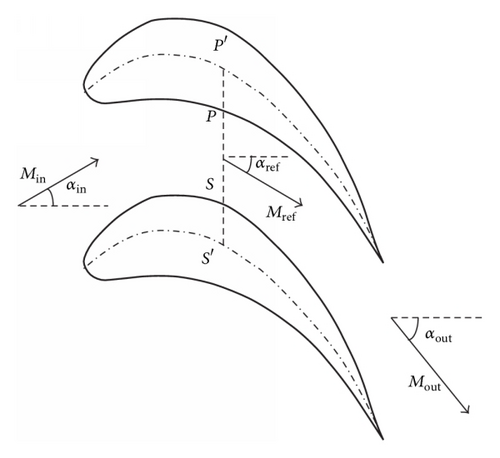
2.3. Deviation Angle Model

Equation (17) indicates that the exit flow angle α_out must be obtained in advance to calculate M_ref. However, in practice, the downstream boundary condition is usually back pressure p_out or exit Mach number M_out rather than α_out. The panel method mentioned above is only able to provide the incompressible exit flow angle, the value of which is obviously different from compressible flow. Under this circumstance, a deviation angle model based on momentum balance is introduced to calculate α_out.

Consider the pressure distribution on the suction and pressure surface of a turbine blade row flow path shown in Figure 4. The circumferential momentum equation of control volume ABCDE is

$$ ()

Assume that ΔF_y ≡ 0; thus, there is

$$ ()

From the continuity equation,

$$ ()

where OP is the opening width, the length of CD.

The expansion from CD to AB is assumed to be isentropic. According to the compressible version of Bernoulli’s equation,

$$ ()

Reorganizing (19), (20), and (21) yields

$$ ()

Since α_op and pitch/OP can be obtained from the blade geometry, (22) can be solved numerically to provide α_out.

3. Comparison of Results

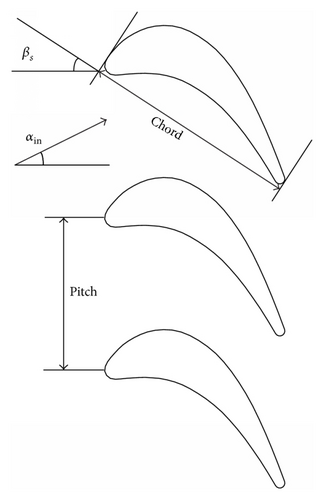
VKI LS 59 turbine cascade data [12] is used to evaluate the modeling method for that its geometry and working condition are similar to those of the aeroengine turbine blades. Lieblein’s method is also used for reference. The blade geometry and general parameters are shown in Figure 5 and Table 1. A FORTRAN computer code of the new method was developed for the calculation. The blade was approximated with 50 elements and the solution required less than 1 second of computer time using a 2.6 GHz Pentium CPU core.

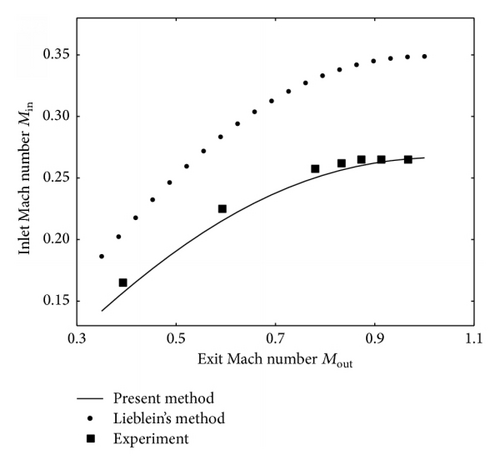
3.1. Inlet Mach Number

In Figure 6, the prediction of the inlet Mach number is compared between the new method, Lieblein’s method, and experimental data. As the experiment data shows, the mass flow will not increase with the exit Mach number as the latter approaches unity. The new method shows better consistency with experimental results.

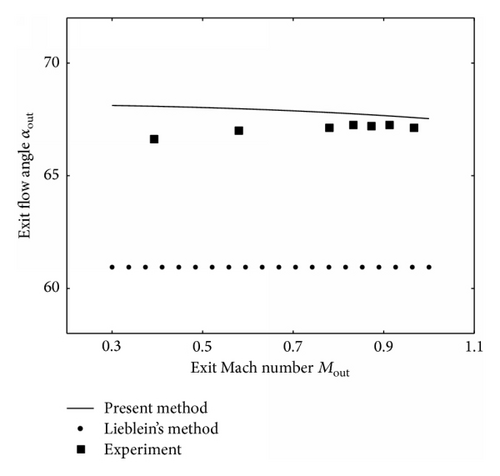
3.2. Exit Flow Angle

The comparison of the exit flow angle is shown in Figure 7. The exit angle of Lieblein’s method does not vary with exit Mach number, since it conserves the mass flow rate of the incompressible solution, which is fixed for a given inlet flow angle, but disagrees with the true value when compressibility effect is strong. In this case, the new method also provides better agreement.

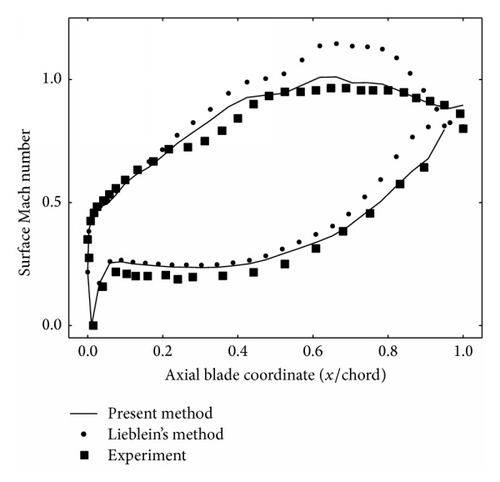
3.3. Surface Mach Number

Figure 8 shows the comparison of the blade surface Mach number distribution. The Mach number given by Lieblein’s method overpredicts the data over the entire blade surface. On the other hand, the new method compares well with the experimental data for the majority of the blade surface.

4. Summary

The panel method has been adopted to calculate the flow through turbine blades. The inherent computational speed and flexibility of the integral equation solution can make this method useful for design calculations. The method presented combines a panel method, a deviation angle model, and a compressibility correction to yield a compressible solution. Comparison with experiment shows that this method is sufficiently accurate to provide a means of selecting aeroengine turbine blade designs for further analysis.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.