Volume 2015, Issue 1 264564

Research Article

Open Access

Scalar Method of Fault Diagnosis of Inertial Measurement Unit

Corresponding Author

Vadym Avrutov

[email protected]

Faculty of Instrument Design and Engineering, National Technical University of Ukraine “Kiev Polytechnic Institute”, Peremogy Avenue 37, Kiev 03056, Ukraine kpi.ua

Search for more papers by this author

Vadym Avrutov,

Corresponding Author

Vadym Avrutov

[email protected]

Faculty of Instrument Design and Engineering, National Technical University of Ukraine “Kiev Polytechnic Institute”, Peremogy Avenue 37, Kiev 03056, Ukraine kpi.ua

Search for more papers by this author

First published: 16 June 2015

https://doi.org/10.1155/2015/264564

Citations: 1

Academic Editor: Kemao Peng

Share a link

Email
Wechat
Bluesky

Abstract

The scalar method of fault diagnosis systems of the inertial measurement unit (IMU) is described. All inertial navigation systems consist of such IMU. The scalar calibration method is a base of the scalar method for quality monitoring and diagnostics. In accordance with scalar calibration method algorithms of fault diagnosis systems are developed. As a result of quality monitoring algorithm verification is implemented in the working capacity monitoring of IMU. A failure element determination is based on diagnostics algorithm verification and after that the reason for such failure is cleared. The process of verifications consists of comparison of the calculated estimations of biases, scale factor errors, and misalignments angles of sensors to their data sheet certificate, kept in internal memory of computer. As a result of such comparison the conclusion for working capacity of each IMU sensor can be made and also the failure sensor can be determined.

1. Introduction

In recent years, the strong requirements for safety of autonomous vehicles caused new demands for reliability of the Inertial Navigation Systems and inertial measurement units as their component parts. It is a reason for increasing and expanding their testing program and using fault diagnosis systems, which includes the capacity of detecting, isolating, and identifying faults.

There are different methods of fault diagnosis systems of Inertial Navigation Systems (INS). More simple and wide application is monitoring of output level of signals of INS components parts made by technology of Built-In Test Equipment (BITE) [1]. Besides, diagnostics could be made by multiple-choice alternative methods of optimal filtration [2–4] and functional diagnostic model methods [5]. If the last mentioned methods are used for IMU and based on application of redundant or extra number of sensors, optimal filtration methods are using whole INS and required other information of instruments, working on diverse form inertial technology principles (e.g., information from satellite navigation receiver or Doppler radar).

The above-mentioned approaches are based on quantitative or numerical models, when using or generating signals that reflect inconsistencies between nominal and faulty system operation.

During the last time many investigations have been made using qualitative or analytical models, using neural networks [6–9] and fuzzy logic techniques [10, 11].

This paper has suggested to use scalar calibration method of gyroscopes and accelerometers [12] for fault diagnosis systems of IMU of Inertial Navigation Systems and also functional diagnostics model methods together, but doing without extra number of sensors—with three gyros and three accelerometers only.

2. Description of the Method

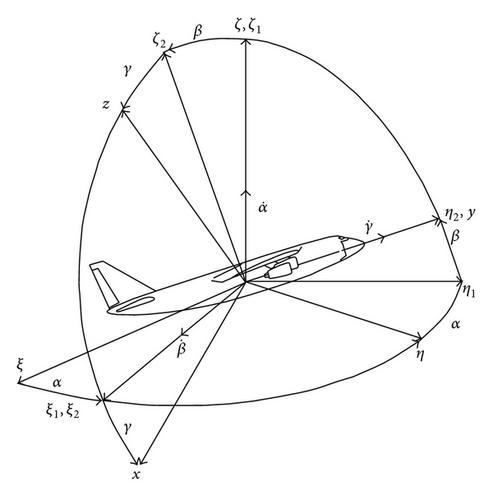
Let IMU of Strapdown INS consist of a triad of single degree-of-freedom gyroscopes G_x, G_y, G_z and a triad of accelerometers A_x, A_y, A_z that are mounted to a vehicle with body frame Oxyz with orthogonal sensitivity axes, as shown on Figure 1.

Details are in the caption following the image — Open in figure viewer PowerPoint

Taking into consideration the errors of instruments (biases and scale factor errors), mounting misalignments of the gyroscopes and accelerometers, which cause cross-coupling terms, and in-run random bias errors, the pendulous accelerometer’s output signals may be expressed as shown below:

In this equation B_ax, B_ay, B_az are the fixed biases, a_x, a_y, a_z are the accelerations acting about the principle axes of the vehicle, M_1a is a 3 × 3 matrix representing scale factor and mounting misalignments, M_2a, M_3a are 3 × 3 matrixes representing the vibropendulous error coefficients [1], and n_ax, n_ay, n_az are the in-run accelerometer’s random bias.

For the linear accelerometers M_2a = M_3a = 0 and (1) could be separated into three equations:

where S_ax, S_ay, S_az are the scale factors of accelerometers, E_ax, E_ay, E_az are a set of the scale factor errors of accelerometers, and Δ_xz, Δ_xy, …, Δ_zx are the mounting misalignments angles or cross-coupling terms [2, 10].

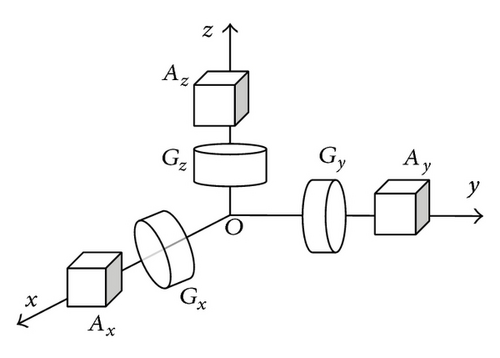
Here, in notification of Δ_xz angle, the first index has shown that the unit is mounted on ox axes and has been rotated about oz axes on Δ_xz angle.

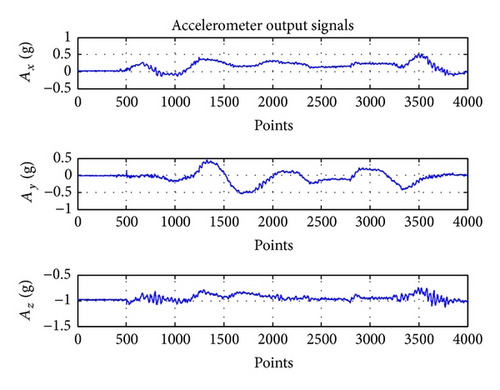
Figure 2 shows examples of real output signals of accelerometers of IMU with USB-port [13] on the moving base.

Let us assume that calibration of IMU has been done before and all the above-mentioned parameters as fixed biases, scale factor errors, and mounting misalignments angles of gyroscopes and accelerometers are measured and reserved in internal INS computer’s memory.

After that we will do scalar diagnostics on fixed foundation in the gravity field of Earth and hence will pass from the acceleration

to gravity vector

; therefore the accelerometer’s output signals (2) will be expressed as shown below:

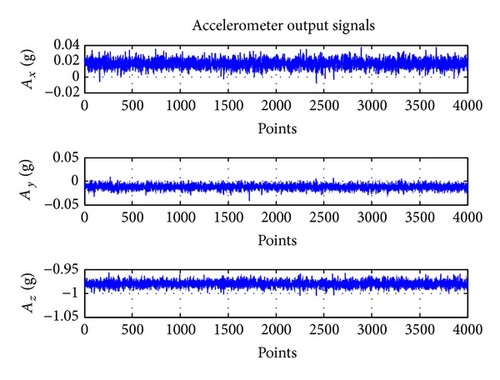
Figure 3 shows examples of real output signals of accelerometers on the fixed base.

Gyro’s output signals may be expressed as shown below:

In this equation B_ωx, B_ωy, B_ωz are the fixed biases, ω_x, ω_y, ω_z are the applied angular rates acting about the principle axes of the vehicle, M_ω is a 3 × 3 matrix representing scale factor and mounting misalignments, M_g, M_g2, M_2g are 3 × 3 matrixes representing the g-dependent bias coefficients and g²-dependent isoelastic coefficients [1], and n_ωx, n_ωy, n_ωz are the in-run gyro’s random bias.

It is noted that listed above model (4) is present for conventional gyroscopes and dynamical tuned gyro.

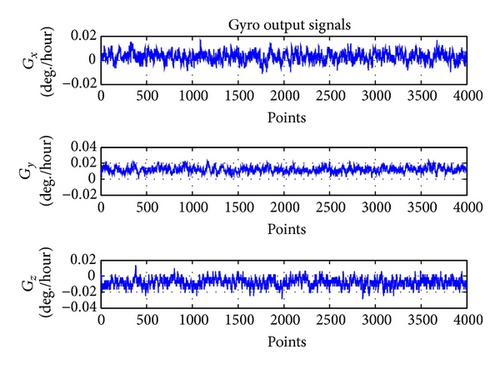
Figure 4 shows examples of output signals of gyroscopes of IMU with USB-port [13] on the moving base.

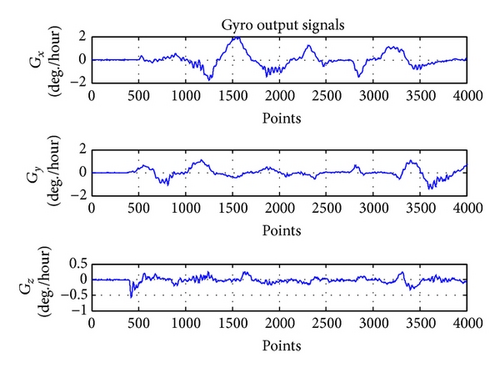
Figure 5 shows examples of output signals of gyroscopes of IMU with USB-port [13] on fixed base.

For stationary base we will pass from the body turn rate

to Earth’s rate

. Besides, for the optical sensors like ring laser and fiber optic gyroscopes, the above-mentioned model (4) could be linearized as following:

We can see that models (3) and (5) are almost similar in form. Therefore let us consider further accelerometer’s model or (3) only. Let us divide every expression of output signal of accelerometer (3) on corresponding scale factor and vector’s module

New denotations of dimensionless output signals and values of right parts will be as follows:

Using denotations (7) the normalized accelerometer’s output signals (6) can be described as

After removal of brackets we will have

According to scalar method of calibration [12] let us sum squared normalized accelerometer’s output signals as following:

It is necessary to calculate the scalar value of measuring vector and compare it to the known scalar value of measurable vector. For that let us remove brackets in right side:

As far as

, ignoring values of the second order to the trifle like (⋯)², for the triad of accelerometers, will get

where

The triad of gyros

analogically will get us the following equation:

Here

Hence, the difference between the scalar value of the normalized measurable vector and its actual value is equal to one, proportional to the errors of the inertial instrument cluster. Coefficients in this dependence are the normalized values of measurable acceleration for accelerometers and angular rate for gyros, their exponential orders, and compositions.

On the basis of (12) and (14) let us build the algorithm of scalar method of quality monitoring for triad of accelerometers and gyros. For sampling time t_k it is possible to establish the following predicates:

Here in right part a value “1” means an operable state of a triad of accelerometers or gyroscopes, a value “0” its failure, and λ_0g a border value of function (1/2)(u_gx² + u_gy² + u_gz² − 1). If the value of function (u_gx² + u_gy² + u_gz² − 1) will not be more than a value 2λ_0g, a triad of accelerometers has been in operable state. If not, therefore there is a failure. The same rule is valid for quality monitoring of gyros.

When the task of the quality monitoring is solved it is necessary to find a place and clear the reason for failure.

3. The Scalar Method of Fault Diagnosis

When the task of the quality monitoring is solved it is necessary to find a place and clear the reason for failure.

To scalar-calibrate the inertial measurement unit we should in the gravity field turn around the certain direction at fixed angles and in every position get the normalized output signals. To solve (12) and (14) it requires at least nine of the inertial measurement unit positions, so number of tests should be more than or equal to nine. The fact is that in each position of the inertial measurement unit its output signals simultaneously have been measuring either gyroscopes or accelerometers, so the minimum number of positions in the two times is less than the total number of required parameters.

Consider (12) and (14) in matrix form:

where u_g, u_Ω are a n × 1 column vectors of the normalized inertial measurement unit output signals:

G, Ω are n × 9 matrixes of normalized projections of the acceleration

and turn rate

of dimension:

e_g, e_Ω are 9 × 1 column vectors of unknown parameters:

Solving the matrix equations (17) by least-squares method, we obtain

where

are estimating values of the unknown parameters of inertial measurement unit.

Thanks to the least-squares method the results are smooth, and as long as average of distribution is equal to zero

the estimated values

will not have a random noise:

When estimated values

are calculated, it is possible to estimate a value of the biases and scalar-factor errors using relations (7):

On the basis of (23) it is possible to create a set of predicates, which are expressed using the algorithm of diagnostics of gyroscopes triad:

Here λ_1ω, λ_2ω, λ_3ω are border values of gyro biases, λ_4ω, λ_5ω, λ_6ω border values of gyro scale factor errors, and λ_7ω, λ_8ω, λ_9ω border values of gyro mounting misalignments. If the difference between calculated values (24) will not be more than a value ±λ_i, a triad of gyroscopes has been in operable state. If not, therefore there is a failure. The number of (25), which is excited out of value ±λ_i, indicates not only that gyro is failure, but also a reason for failure: excessing of real biases, scale factor errors, or mounting misalignments to their nominal values.

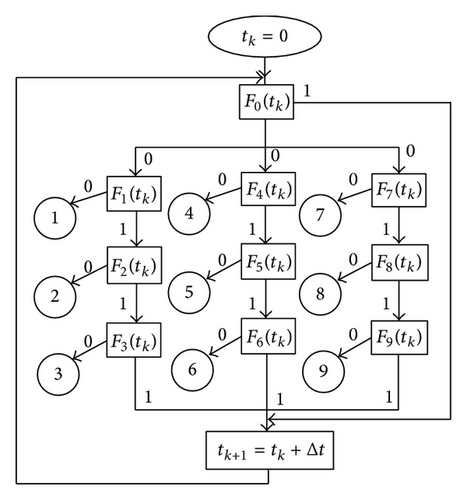
The scheme of scalar method of fault diagnosis systems of IMU is depicted in the Figure 6. Here numbers 1,2, 3 are shown in the gyro’s failures via biases discrepancy, numbers 4,5, 6 in gyro’s failures via scale factor errors discrepancy, and numbers 7,8, 9 in gyro’s failures via mounting misalignments discrepancy.

Analogically we can get the algorithm of scalar method of diagnostics of accelerometers triad:

Here λ_1a, λ_2a, λ_3a represent border values of accelerometers biases, λ_4a, λ_5a, λ_6a border values of accelerometers scale factor errors, and λ_7a, λ_8a, λ_9a border values of accelerometers mounting misalignments. If the difference between calculated values

will not be more than a value ±λ_i, a triad of accelerometers has been in operable state. If not, therefore there is a failure. The number of

, which is excited out of value ±λ_i, indicates not only what accelerometer is failure, but also a reason for failure: excessing of real biases, scale factor errors, or mounting misalignments to their nominal values.

4. Simulations

Simulation was proceed at latitude φ = 50^° (Kiev city location) on static or fixed base. The parameters of gyros are set as the following normalized values:

We assume that IMU is rotating for Euler-Krylov angles α, β, γ about axis oxyz as illustrated in Figure 7.

Output signals of IMU’s gyros were used for calculation of estimated values of (23).

At first we need to calculate

for gyro outputs and

for accelerometers:

Here

-direction cosines matrix.

To avoid a problem of singularity solving (17) by least-squares method we have used quaternion

where quaternion’s components can be expressed via angles α, β, γ,

and known relationship between matrix of direction cosines and quaternion’s components:

Using matrix equations (28) it is possible to receive normalized values:

Table 1 presents IMU positions for calculations of output signals of gyros.

1. Values of three angles in degrees of IMU positions.

Position number	Beta (deg.)	Gamma (deg.)
1	0	−90
2	0	90
3	90	0
4	−90	0
5	0	0
6	0	180
7	−90	−45
8	90	45
9	180	−45
10	0	45
11	135	0
12	−45	0
13	90	−45
14	90	135
15	0	−45
16	0	135
17	45	0
18	−135	0

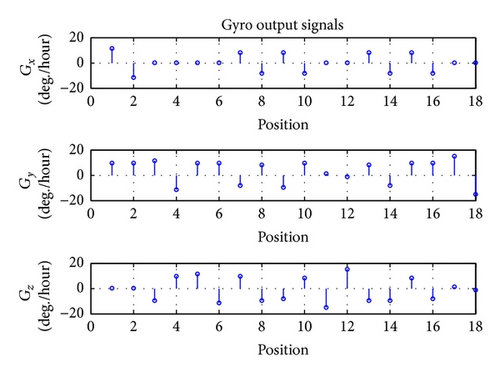
Figure 8 shows output signals of gyroscopes, which were calculated by (5) for IMU positions of Table 1.

Good results were received (error between nominal value and estimated value on static base not more than 5%) and it was shown [12] that absolute value of relative error of the biases depends on the number of digits after the decimal point in the output signals of gyro and accelerometers. In other words it requires sufficiently high accuracy of measurement of the output signals of sensors.

5. Conclusions

In this paper we have proposed a new method of fault diagnosis systems IMU of Strapdown Inertial Navigation Systems. The scalar calibration method is a base of the scalar method of quality monitoring and diagnostics. In accordance with scalar calibration method algorithms of fault diagnosis systems are developed. As a result of quality monitoring algorithm verification is implemented in the working capacity monitoring of IMU. A failure element determination is based on diagnostics algorithm verification and after that the reason for such failure is cleared.

The process of verifications consists of comparison of the calculated estimations of biases, scale factor errors, and misalignments angles of sensors to their data sheet certificate, kept in internal memory of computer. As a result of such comparison the conclusion for working capacity of each IMU sensor can be made and also the failure sensor can be determined.

Conflict of Interests

The author declares that there is no conflict of interests regarding the publication of this paper.

References

1 Titterton D. and Weston J., Strapdown Inertial Navigation Technology, 2004, 2nd, Institution of Electrical Engineers, London, UK.
10.1049/PBRA017E
Web of Science® Google Scholar
2 Dmitriev S. P., Kolesov N. V., and Osipov A. V., Reliability of the navigation systems with consideration for information failures, Proceedings of the 10th Saint Petersburg International Conference on Integrated Navigation Systems, May 2003, Saint Petersburg, Russia, 102–103.
Google Scholar
3 Dmitriev S. P., Osipov A. V., and Koshaev D. A., Detection of information failures in marine navigation systems and their reconditioning, Proceedings of the 6th IFAC Symposium on Fault Detection, Supervision and Safety of Technical Processes, 2006, Beijing, China, 1491–1496.
Google Scholar
4 Dmitriyev S. P., Stepanov O. A., and Shepel S. V., Nonlinear filtering methods: application in INS alignment, IEEE Transactions on Aerospace and Electronic Systems. (1997) 33, no. 1, 260–272, https://doi.org/10.1109/7.570762, 2-s2.0-0030736044.
10.1109/7.570762
Web of Science® Google Scholar
5 Kulik A. S., Chukhray A. G., and Bastide J. P. M., The hardware-software complex for teaching of fault-tolerant systems developers, Proceedings of the 5th International Conference on Physics and Control (PhysCon '11), 2011, Leon, Spain.
Google Scholar
6 Patton R. J., Frank P. M., and Clark R. N., Issues of Fault Diagnosis for Dynamic Systems, 2000, Springer, London, UK.
10.1007/978-1-4471-3644-6
Web of Science® Google Scholar
7 Chen J. and Patton R. J., Robust Model Based Fault Diagnosis for Dynamic Systems, 1999, Kluwer Academic Publishers, New York, NY, USA.
10.1007/978-1-4615-5149-2
Google Scholar
8 Kolesov N. V., Fault diagnosis in dynamic systems using fuzzy interacting observers, Advances in Fuzzy Systems. (2013) 2013, 9, 874393, https://doi.org/10.1155/2013/874393, 2-s2.0-84876537400.
10.1155/2013/874393
Google Scholar
9 Bezmen G. V. and Kolesov N. V., Program models for diagnosis of information control systems, Programming and Computer Software. (2014) 40, no. 5, 250–258, https://doi.org/10.1134/S0361768814050028.
10.1134/S0361768814050028
Web of Science® Google Scholar
10 Evsukoff A., Gentil S., and Montmain J., Fuzzy reasoning in co-operative supervision systems, Control Engineering Practice. (2000) 8, no. 4, 389–407, https://doi.org/10.1016/S0967-0661(99)00170-7, 2-s2.0-0033901218.
10.1016/S0967-0661(99)00170-7
Web of Science® Google Scholar
11 Yang H. T. and Liao C. C., Adaptive fuzzy diagnosis system for dissolved gas analysis of power transformers, IEEE Transactions on Power Delivery. (1999) 14, no. 4, 1342–1350, https://doi.org/10.1109/61.796227, 2-s2.0-0033207486.
10.1109/61.796227
CAS Web of Science® Google Scholar
12 Avrutov V., On scalar calibration of an inertial instrument cluster, Innovation and Technologies News. (2011) 2, no. 11, 22–30.
Google Scholar
13 Avrutov V. and Sturma I., Inertial measurement unit with USB-Port, Proceedings of the 19th Saint Petersburg International Conference on Integrated Navigation Systems (ICINS '12), May 2012, Saint Petersburg, Russia, State Research Center (CSRI) Elektropribor, 194–195.
Google Scholar

Citing Literature

All articles

Scalar Method of Fault Diagnosis of Inertial Measurement Unit

Abstract

1. Introduction

2. Description of the Method

3. The Scalar Method of Fault Diagnosis

4. Simulations

5. Conclusions

Conflict of Interests

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Scalar Method of Fault Diagnosis of Inertial Measurement Unit

Abstract

1. Introduction

2. Description of the Method

3. The Scalar Method of Fault Diagnosis

4. Simulations

5. Conclusions

Conflict of Interests

References

Citing Literature

Figures

References

Related

Information