Inverse Problem of Air Filtration of Nanoparticles: Optimal Quality Factors of Fibrous Filters
Abstract
Application of nanofibers has become an emerging approach to enhance filtration efficiency, but questions arise about the decrease in Quality factor (QF) for certain particles due to the rapidly increasing pressure drop. In this paper, we theoretically investigate the QF of dual-layer filters for filtration of monodisperse and polydisperse nanoparticles. The inverse problem of air filtration, as defined in this work, consists in determining the optimal construction of the two-layer fibrous filter with the maximum QF. In comparison to a single-layer substrate, improved QF values for dual-layer filters are found when a second layer with proper structural parameters is added. The influences of solidity, fiber diameter, filter thickness, face velocity, and particle size on the optimization of QF are studied. The maximum QF values for realistic polydisperse particles with a lognormal size distribution are also found. Furthermore, we propose a modified QF (MQF) accounting for the effects of energy cost and flow velocity, which are significant in certain operations. The optimal MQF of the dual-layer filter is found to be over twice that of the first layer. This work provides a quick tool for designing and optimizing fibrous structures with better performance for the air filtration of specific nanoparticles.
1. Introduction
The design of fibrous filters is based on the fact that filtration behavior is highly dependent on filter structure, particle size, and flow pattern. In general, filtration mechanisms that rely on mechanical capture include interception, diffusion, and inertial impaction [2]. A minimum at the most penetrating particle size (MPPS) usually exists between 0.1 and 0.5 μm due to the combined action of these filtration mechanisms, which have different sensitivities to particle size [3]. In comparison to coarse fibers, the use of fine fibers as a filter engenders a smaller MPPS and higher filtration efficiency. However, the pressure drop of filters composed of finer fibers becomes much greater as it decreases with the square of fiber radius, even for extremely fine nanofibers with a slip flow condition [4, 5]. Moreover, a random and inhomogeneous fiber arrangement makes the actual filter more permeable but less efficient in filtration than ordered fiber arrays [6–8]. Therefore, an inhomogeneity factor has been introduced to fit the order-based model to experimental results [9]. The filtration efficiency of filters varies with the face velocity and the MPPS shifts accordingly as well [10].
Utilization of nanofibers has become an emerging approach to enhance air filtration efficiency [11–16]. A composite of microfibers and nanofibers has been found to significantly improve the capture efficiency and QF for MPPS, whereas a single layer of nanofibers only leads to an increase in QF for very large particles [3, 17]. The QF for a dual-layer filter manufactured by the melt-blown technique is much higher than that of the microfiber substrate alone, as the increase in filtration efficiency is not overpaid with an excessive pressure drop [3]. Filtration tests have also indicated that a microfiber substrate layered by a single nanofiber mat of 0.15 μm diameter has a higher QF than conventional fiberglass filters for particles larger than 0.5 μm [18]. The QF for nanoparticles is observed to decline with a decrease in nanofiber diameter whereas the QF for larger particles increases with increasing nanofiber diameter [18]. It is believed that, for nanoparticles, the pressure drop increases more rapidly than the filtration efficiency due to diffusion; for large particles, the filtration efficiency predominated by interception and inertial impaction increases more rapidly than the pressure drop [17]. For a dual-layer filter with mean fiber diameters 14.7 μm and 0.208 μm, respectively, filtration performance has been found to decrease with face velocity [10]. This phenomenon is caused by the much lower likelihood for particles to collide on fibers through diffusion filtration at a smaller face velocity. Enhanced QF has also been observed in a thick layer alone in comparison to multiple thin layers of electrospun nanofibers, as multilayer filters have greater uniformity and smaller fiber sizes [19].
The QF of fibrous filters is also improved by modification of the morphology, including adding beaded nanofibers [20], coating multisize nanoparticles on electrospun nanofibers [21], depositing a low amount of carbon nanotube (CNT) films [22], and in situ growth of brush-like CNTs on quartz fibers [23, 24]. The results of increased QF and the possible explanations are summarized in Table 1.
| Type | Improved performance | Possible reasons | Reference |
|---|---|---|---|
| Adding beaded nanofibers | Exhibited better filtration performance for aerosol particles ranging from 20 to 300 nm than nanofibers and particle/nanofiber composites | Increased void volume and aspect ratio | [20] |
| Coating multisize nanoparticles on electrospun nanofibers | Complimentary filtration efficiency (99.989%) and pressure drop (117 Pa) for 300–500 nm NaCl aerosol particles | Rough surface and noncircular cross section of fibers | [21] |
| Depositing a low amount of carbon nanotube (CNT) films | Filtration efficiency >99% in all cases and meeting the guidelines of HEPA filters; higher pressure drops but better QFs than the substrate | A broad micropore size distribution and a few mesopores between CNTs | [22] |
| In situ growth of brush-like CNTs on quartz fibers | Pressure drop moderately enhanced, but QF improved fairly well | Slightly reduced pore sizes, much larger specific surface area | [23, 24] |
The filtration quality of a clean filter is not sensitive to the deposition of particles in a short period, but it is strongly affected by particle loading over a long term [1]. With solid particles clogging to form a dust cake in the filter, flow resistance increases exponentially and penetration decreases at a given flow rate [1]. It is interesting to see that the deposited particles are more efficient in filtration than the fibers, as dendrite aggregate is formed with a high specific surface. To take into account continuous and unsteady loading of particles, a more realistic criterion of filtration performance, namely, the filter utility factor (FUF), has been proposed [25]. A cost-effective filter with higher dust-holding capacity has also been designed based on graded fibrous media [25]. The arrangement of a microfiber substrate in front of a nanofiber layer also gives a filter high filtration efficiency in the initial stage and a low increase in drop during continuous loading [26].
From the above discussion we find that there is less concern to design and optimize the fibrous filters to maximize the QF for nanoparticles. Layering of nanofibers onto a microfiber substrate leads to an increased QF over a certain range of particle size, but it may decrease the QF for the other particles. In practical filtration processes, the aim is often to capture particles of a specific size, such as the MPPS, the mean particle size, or the highest proportion particle size. Hence, as an inverse problem, in addition to avoiding any decrease in QF, we attempt in this paper to determine the optimal structural parameters that lead to the maximum QF for these target nanoparticles based on a dual-layer fibrous filter as illustrated in Figure 1. Here, the first layer is fixed while the second layer varies with different solidity, fiber diameter, and thickness. Furthermore, QF has been found not to be an energy-cost-based index [1]. To this end, we explore the filtration performance of dual-layer fibrous filters on the basis of a modified QF (MQF), by concerning energy cost and flow velocity.
2. Analysis of Theoretical Expressions
This study concerns the filtration of fine particles in clean filters. The assumptions are made that particle clogging is negligible and no particle rebounds from the fiber.
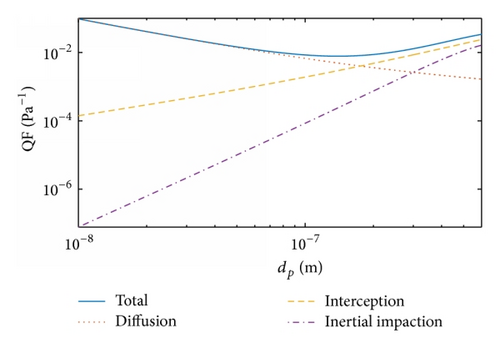
In Figure 2, we examine the effects of filtration mechanisms on the QF of a single-layer fibrous filter. The QFs for diffusion-only, interception-only, inertial impaction-only, and the combined filtration mechanisms are compared at U = 0.1 m/s, df = 1 μm, c = 0.05, and h = 1 mm. For nanoparticles (below 0.1 μm), the QF based on the combined filtration mechanisms decreases with an increase in particle size, approaching the diffusion-only QF. For micro and submicro particles (above 0.1 μm), the total QF based on the combined filtration mechanisms increases with an increase in particle size, which is consistent with the interception-only and inertial impaction-only cases. We find that diffusion filtration is dominant for nanoparticles and submicro particles (<1 μm) whereas interception and inertial impaction become more critical to the QF in the range of large particles (>3 μm). It is expected that very small particles are captured through random collision with fibers due to Brownian motion. Larger particles are intercepted by fibers in the path of the air stream or deviate from the path and then compact fibers due to inertia. The concave curves in Figure 2 indicate that the values of QF vary with particle size under different filtration mechanisms, which is similar to those of filtration efficiency. For improvement of QF, therefore, it is essential to consider all three filtration mechanisms simultaneously.
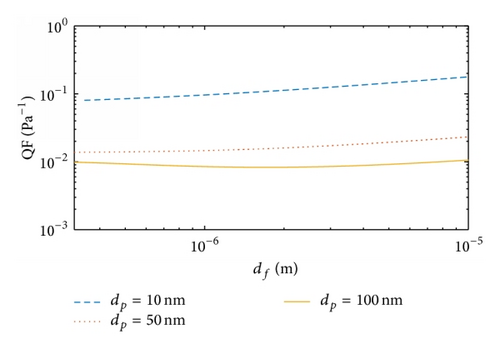
Capture of particles of a given size is of great interest in specific filtration. In Figure 3, we investigate the effect of fiber diameter on the QF of a single-layer filter, by capturing nanoparticles with diameters 0.01 μm, 0.05 μm, and 0.1 μm. The fiber diameter varies from 0.3 μm to 10 μm, the filter thickness is 1 mm, the face velocity is 0.1 m/s, and the solidity is 0.05. We observe that the QF for particles of 0.01 μm and 0.05 μm increases monotonously with the increase in fiber diameter. The reason is that the pressure drop decreases more rapidly than the decrease in filtration efficiency with increasing fiber diameter. For nanoparticles of 0.1 μm, it is interesting to find the minimum QF from the concave line in Figure 3. This phenomenon reveals the complexity of the dependence of the QF on the structural parameters, as the decrease in the pressure drop can be outweighed by the decrease in filtration efficiency.
3. QF and MQF of Dual-Layer Filters
The first layer is set as the control sample, so P1 and Δp1 are fixed. And the QF varies with the structural parameters of the second layer, namely, c2, h2, and df2.
4. Results and Discussion
To find the optimal filtration performance, we focus on investigating the QF for a dual-layer filter with the first layer fixed while the second layer varied (Figure 1). The models we employ in this paper, including (4), (7), and (8) for filtration efficiency of single-layer or dual-layer fibrous filters and (9) for pressure drop of fibrous filters, have been well verified by experimental results [5, 18]. The structural parameters of three types of the first, fixed layers are summarized in Table 2. The second layers have different solidity, thickness, and fiber diameter, and the face velocity is set as U = 0.1 m/s. We focus mainly on the filtration of particles of a specific size, but we still examine the effect of the polydispersity degree of the particles on the QF. Since the filtration of nanoparticles is less understood [1] and the MPPS is often around 100 nm [3, 17], we focus on the QF of nanoparticles with dp = 10 nm and dp = 100 nm. It is noted that QF is not the only criterion by which the filter quality is measured [17]; the evaluation depends on target requirements and specific operating conditions. Thus, we also explore the MQF by considering the influence of energy cost and flow velocity.
| Type | c1 | df1 | h1 |
|---|---|---|---|
| 1 | 0.1 | 10 μm | 3 mm |
| 2 | 0.05 | 2 μm | 1 mm |
| 3 | 0.01 | 0.4 μm | 0.2 mm |
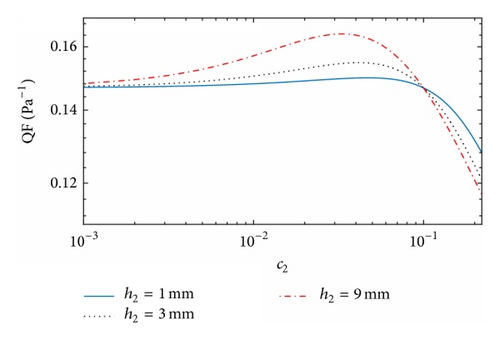
For the filter of Type 1, variations of QF against c2 and df2 at U = 0.1 m/s, dp = 10 nm, h1 = 3 mm, and h2 = 1, 3, 9 mm are shown in Figure 4. The concave curves in Figure 4(a) indicate the optimal filters with the highest QF against c2 when c1 is equal to 0.1. The maximum QF results vary with the corresponding values of c2, which are around 0.04, 0.05, and 0.06 for h2 = 1, 3, 9 mm, respectively. In addition, the maximum QF increases with the increase in h2. It is noted that the three filters have the same QF when c2 = c1 = 0.1 at the crossover of curves, and the dual-layer filter becomes a single-layer filter with its QF independent of thickness. When c2 > 0.1, the QF values decrease dramatically with the increase in c2, revealing the inefficiency of the filters in capturing the particles of dp = 10 nm. This finding is consistent with the experimental results that the highest QF is found within five different values of c2 for a nanofiber-microfiber dual-layer filter [18]. For the filtration of the particles with dp = 100 nm, Figure 4(b) shows a similar trend of the QF against c2. However, the maximum QF values for dp = 100 nm are much smaller than those for dp = 10 nm. Hence, the dual-layer filters with df1 = df2 = 10 μm have a better filtration performance for fine particles, which is similar to that of the single-layer filter. Figures 4(c) and 4(d) show the dependence of QF on df2 for dp = 10 nm and dp = 100 nm, respectively. Here, we have c2 = c1 = 0.1, h1 = 3 mm, and h2 = 1, 3, 9 mm. In Figure 4(c), the maximum QF results are found against df2, with the corresponding values of df2 equal to 1.5 μm, 2 μm, and 2.5 μm for h2 = 1, 3, 9 mm, respectively. When df2 is smaller than df1 = 10 μm, the QF decreases considerably with the decrease in df2. Therefore, the addition of nanofibers onto the substrate or the first layer might not be reasonable in this case, although the filtration efficiency of nanofibers is much higher. In Figure 4(d), the maximum QF values for dp = 100 nm are much lower than those for dp = 10 nm in Figure 4(c). The maximum QFs observed in Figures 4(c) and 4(d) look slightly higher than the QF of a single-layer filter, but selection of the optimized second layer avoids the significant decline in QF caused by using inappropriate fibers. Figure 4 also demonstrates that two layers with close fiber diameters or solidity have higher QF than those with a very broad difference in fiber size or solidity.
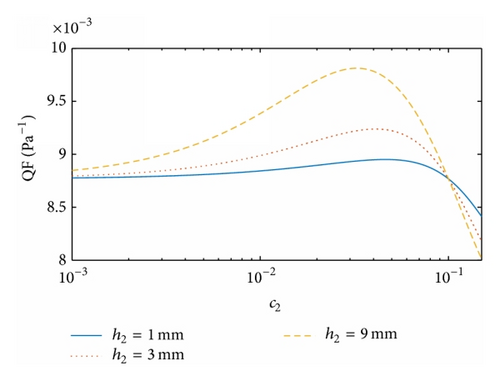
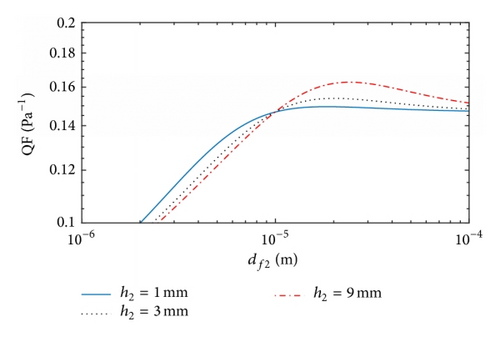
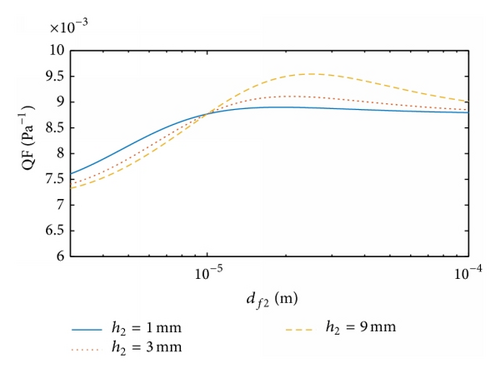
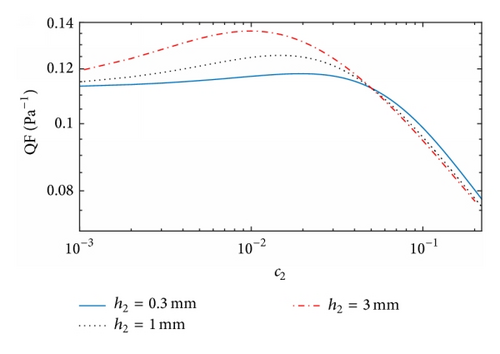
Figures 5 and 6 illustrate the dependence of the QF on the structural parameters for the dual-layer filters Type 2 and Type 3, respectively. As for Type 1, their maximum QF results are found at different thickness ratios, with the corresponding values of c2 slightly smaller than c1 while the corresponding values of df2 are moderately larger than df1.
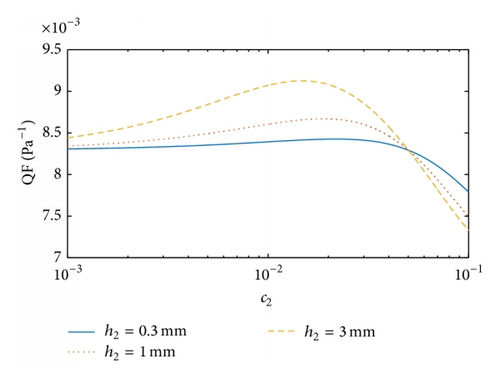
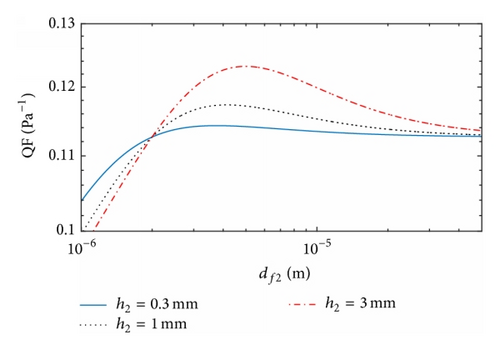
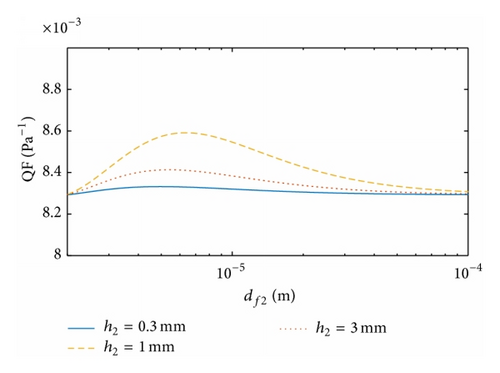
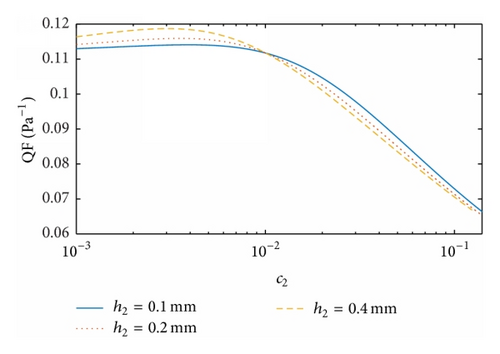
In Figure 7 we study the effects of face velocity on the QF of the dual-layer filter against df2 at dp = 100 nm, h1 = h2 = 3 mm, df1 = 10 μm, and c1 = c2 = 0.1. The maximum QF values are visible and they increase with the decrease in U. It is feasible to argue that a smaller face velocity ensures more adequate contact between fibers and particles, yielding a higher QF. However, a very small U can slow down the filtration processes even though the QF is satisfactory. Hence, we optimize the filter on the basis of the QF in the desired range of face velocity.
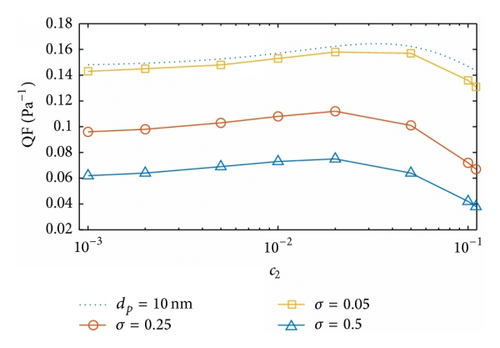
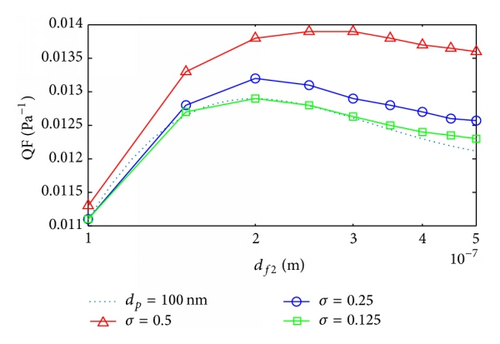
In Figure 8 we compare the QF values between monodisperse and polydisperse particles with the same mean particle size. The solidity of the second layer c2 varies in Figure 8(a), with 〈dp〉 = 100 nm, c1 = 0.1, h1 = 3 mm, h2 = 9 mm, df1 = df2 = 10 μm, and U = 0.1 m/s. Figure 8(b) demonstrates the dependence of QF on the fiber diameter of the second layer df2, with 〈dp〉 = 10 nm, c1 = c2 = 0.01, h1 = h2 = 0.2 mm, df1 = 0.4 μm, and U = 0.1 m/s. The particle size follows a lognormal distribution with different scale parameters σ. For the monodisperse particles, the maximum QF results are found for polydisperse particles. With increasing σ and the narrowing distribution of particle size, the maximum QF values increase as df2 at c1 = c2 but decrease as c2 at df1 = df2. It is demonstrated that the value of QF of the dual-layer filter against polydisperse particles is increased by around 10% than that of the fixed single first layer, which is equivalent to the two-layer fibrous filter with the solidity of the second layer extremely small. When σ is very small, the QF curves of for polydisperse particles nearly overlap with those of monodisperse particles, as expected. It is interesting to note that the optimal structural parameters accounting for the maximum QF are close between monodisperse and the polydisperse particles.
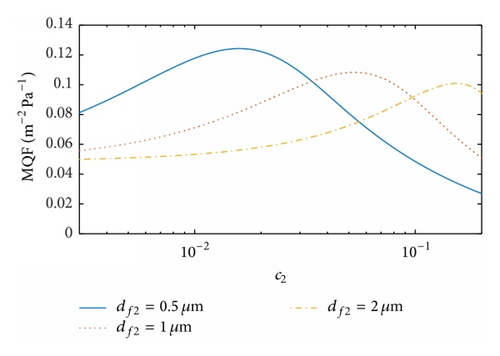
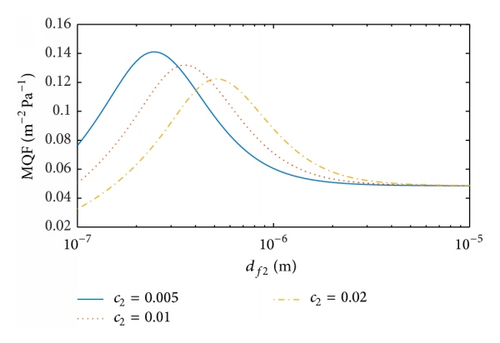
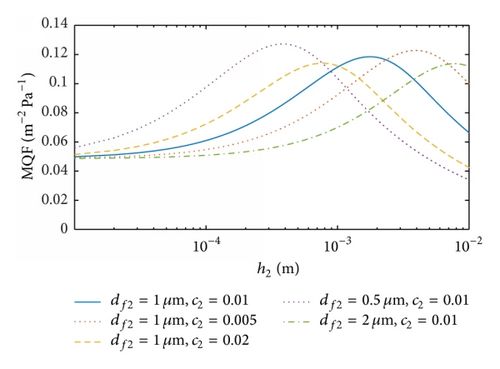
The maximum MQF values of the dual-layer filter against the solidity, the fiber diameter, and the thickness of the second layer are shown in Figures 9(a), 9(b), and 9(c), respectively. We set G = 3.28 W and S = 0.005 m2 for a fibrous filter in a commercial respirator at U = 0.1 m/s. The values of G and S are determined by the target filters and operating conditions. In Figure 9(a), we have c1 = 0.01, df1 = 1 μm, h1 = h2 = 0.2 mm, and dp = 100 nm, and the maximum MQF values of the dual-layer filter are found against c2 at df2 = 0.5, 1, 2 μm. The maximum MQF results decrease with increases in c2 and the corresponding values of c2 vary considerably for different c1, which is unlike the QF responses. The optimal MQF of the dual-layer filter is found to be over twice of that of the fixed single first layer. In Figure 9(b), the maximum values of MQF are found against df2 at c2 = 0.005, 0.01, 0.02, and they decline with increasing df2. The corresponding values of df2 for the maximum MQF are smaller than df1, which is also unlike that for QF. Finally, in Figure 9(c) the dependence of MQF on h2 is investigated at c2 = 0.005, 0.01, 0.02 with df2 = 1 μm and df2 = 0.5, 1, 2 μm with c1 = 0.01. The maximum MQF increases with increasing df2 but decreases with the increase in c2. Among the different cases, the values of h2 corresponding to the maximum QF vary considerably, indicating the significance of choosing the appropriate thickness of the dual-layer filter to improve filtration performance. To summarize, the requisite conditions for the optimal QF are based on the fact that the total filtration efficiency has a slower decrease rate before the threshold of structural parameters is reached but then a faster decrease rate than the total pressure drop at the given energy cost.
5. Conclusion
- (i)
The maximum QF for the capture of monodisperse and polydisperse nanoparticles is found against the variation of solidity, thickness, and fiber diameter of the second layer, when the first layer is fixed.
- (ii)
Under a given energy cost, the optimal filters are found with the highest MQF against variations of solidity, thickness, and fiber diameter of the second layer when the first layer is fixed.
- (iii)
The optimal QF of the dual-layer filter is enhanced by around 10% than that of the fixed first layer, while the maximum MQF can be increased to be over twice in certain cases.
- (iv)
The optimal structural parameters accounting for the maximum QF vary with face velocity and particle size distribution.
This work provides a quick tool to design and optimize fibrous filters with better filtration performance of nanoparticles. To avoid expensive computation, current studies are limited to the filter fibers with constant diameter and circular shape and they also assume negligible clogging of particles. The above concerns will be addressed in future work with the assistance of the Computational Fluid Dynamics (CFD) technique. As well, optimization of the fiber surface roughness, the sizes of the nanorods grown on the fiber wall, and the clogging distribution in different filter layers will also be explored to prompt the best filtration performance.
Conflict of Interests
The authors declare that there is no conflict of interests regarding the publication of this paper.
Acknowledgment
The coauthors Jintu Fan and Xiaoming Qian acknowledge the funding support of Tianjin City Applied Foundation & Emerging Technology Research Program (Grant no. 15JCZDJC38500).




