Modified Theories of Gravitation behind the Spacetime Deformation
Abstract
In the framework of proposed theory of spacetime deformation/distortion, we have a way to deform the spacetime through a nontrivial choice of the distortion-complex, displaying different connections, which may reveal different post-Riemannian spacetime structures as corollary. We extend this theory to address, in particular, the gauge model of the most general metric-affine gravity carrying both nontrivial torsion and nonmetricity. This model is constructed in the framework of the first order Lagrangian expressed in terms of the gauge potentials and their first derivatives. The equations of the standard theory, which have no propagating modes for torsion, can be equivalently replaced in modified framework by the modified equations, which in the limit of reducing the affine group leads to the modified Einstein-Cartan theory with dynamical torsion and beyond. In testing the modified framework for various particular cases, we use the Lagrange multipliers for extinguishing nonmetricity and torsion.
1. Introduction
We will not attempt a history of gauge theory of gravitation in general, but only of those that seem most relevant to the particular theory of this paper. From its historical development, the efforts in gauge treatment of gravity mainly focus on the quantum gravity and microphysics, with the recent interest, for example, in the theory of the quantum superstring or, in the very early universe, in the inflationary model. The papers on the gauge treatment of gravity provide a unified picture of gravity modified models based on several Lie groups [1–61]. However, currently no single theory has been uniquely accepted as the convincing gauge theory of gravitation which could lead to a consistent quantum theory of gravity. They have evoked the possibility that the treatment of spacetime might involve non-Riemannian features on the scale of the Planck length. This necessitates the study of dynamical theories involving post-Riemannian geometries. On the other hand, a general way to deform the spacetime metric with constant curvature has been explicitly posed by [62–66]. The problem was initially solved only for 3D spaces, but consequently it was solved also for spacetimes of any dimension. It was proved that any semi-Riemannian metric can be obtained as a deformation of constant curvature matric, with this deformation being parameterized by a 2-form. A novel definition of spacetime metric deformations, parameterized in terms of scalar field matrices, is proposed by [67]. However, without care of the historical justice and authenticity, it also should be emphasized that the continuous deformations within the space of connections were studied by [17, 18]. This concept of a deformation seems to be a special case of a prolongation. A main idea is as follows: since any tensor-valued one-form transforms homogenously with respect to linear gauge transformations, its subtraction from a connection can be regarded as a continuous deformation within the space of connections. A more general approach is suggested by [68], whereas the authors present the extension to 4D of an euclidean 2D model that exhibits spontaneous generation of a metric. In this model gravitons emerge as Goldstone bosons of a global SO(D) × GL(D) symmetry broken down to SO(D). They formulated microscopic theory without having to appeal to any particular spacetime metric and only assume the preexistence of a manifold endowed with an affine connection. Moreover, here it seems that not even a flat metric needs to be assumed. In this sense the microscopic theory is quasitopological. The vierbein appears as a condensate of the fundamental fermions. In spite of having nonstandard characteristics, the microscopic theory appears to be renormalizable. Recently, some clarifications are also collected in the book [69], where the authors have tried to collect the established results and to focus new investigations on the real loopholes of the theory. Only time will tell whether any of these intriguing theories is correct and which of the hypothesized hidden symmetries is actually realized in nature.
It is well known that the notions of space and connections should be separated; see, for example, [13, 70–72]. The curvature and torsion are in fact properties of a connection, and many different connections are allowed to exist in the same spacetime. Therefore, when considering several connections with different curvature and torsion, one takes spacetime simply as a manifold and connections as additional structures. Allowing minimal departure from semi-Riemannian geometry would consist in admitting torsion. The concept of a linear connection as an independent and primary structure of spacetime is the fundamental proposal put forward by Cartan’s geometrical analysis [43–46], whereas he gave a beautiful geometrical interpretation of torsion representing a translational misfit. The Einstein-Cartan (EC) theory also called Einstein-Cartan-Sciama-Kibble theory is the minimal extension of the general relativity, which considers curvature and torsion as representing independent degrees of freedom. In the standard EC theory, the equation defining torsion is of algebraic type, and not a differential equation, and no propagation of torsion is allowed. Even at the textbook level it was common knowledge known from the weak interaction that the causality reasons do not respect a contact interaction. Therefore, many modifications of the EC theory have been proposed in recent years; see, for example, [37, 73–79], but all these approaches are subject to many uncertainties. In particular, in [80] the authors analyze the functional renormalization group flow of quantum gravity on the EC theory space. The latter consists of all action functionals depending on the spin connection and the vielbein field (coframe) which are invariant under both spacetime diffeomorphisms and local frame rotations. They find evidence for the existence of at least one non-Gaussian renormalization group fixed point which seems suitable for the asymptotic safety construction in a setting where the spin connection and the vielbein are the fundamental field variables. The difference between Einstein’s general relativity and its Cartan extension is analyzed within the scenario of asymptotic safety of quantum gravity by [81], whereas it was found that the four-fermion interaction distinguishes the Einstein-Cartan theory from its Riemannian limit. However, modifications of EC theory are intricate. In a recent paper [82], we construct the two-step spacetime deformation (TSSD) theory which generalizes and, in particular cases, fully recovers the results of the conventional theory of spacetime deformation [62–66]. Conceptually and techniquewise the TSSD theory is versatile and powerful and manifests its practical and technical virtue in the fact that through a nontrivial choice of explicit form of a world-deformation tensor, which we have at our disposal, in general, we have a way to deform the spacetime displaying different connections, which may reveal different post-Riemannian spacetime structures as corollary: (1) the Weitzenböck spacetime structure—(W4) underlying a teleparallelism theory of gravity, see, for example, [23, 24, 38, 83–93]; (2) the RC manifold—(U4) underlying EC theory, for a comprehensive references, see, for example, [34–37, 51, 52, 94]; (3) or even the most general linear connection of metric-affine gravity (MAG) taking values in the Lie algebra of the 4D-affine group, A(4, R) = R4 GL(4, R); see, for example, [15–18, 42–50, 55–57]. This represents the semidirect product of the group of 4D-translations and general linear 4D-transformations. Continuing along this line, in the present paper, we address the essential features of the gauge model of the most general MAG theory in context of TSSD-construction of post-Riemannian geometry, whereas to complete the TSSD theory, we build up the distortion-complex (DC) and show how it restores the world-deformation tensor, which still has been put in [82] by hand. A formulation of the major physical aspects of the modified gauge MAG theory will be given in the framework of the first order Lagrangian expressed in terms of the gauge potentials and their first derivatives. All the fundamental gravitational structures in fact, the metric as much as the coframes and connections, acquire a DC induced theoretical interpretation. There is another line of reasoning which supports the side of this model. We address the key problem of a dynamical torsion and show that the equations of the standard MAG theory can be equivalently replaced by the set of modified MAG equations in which the torsion, in general, is turned out to be dynamical. We define the physical conditions for the spacetime deformations when the spin-spin interaction becomes short-range propagating. As an application we have to test the general TSSD-MAG framework in some limit, namely, we have to put on Lagrange multipliers to recover the TSSD versions of different (sub)cases of Poincaré gauge theory (PG), Einstein-Cartan theory, teleparallel gravity (GR||), and general relativity (GR). This allows amplifying and substantiating the assertions made in [82]. Moreover, imposing different physical constraints upon the spacetime deformations, in this modified framework we may reproduce the term in the well known Lagrangian of pseudoscalar-photon interaction theory, or terms in the Lagrangians of pseudoscalar theories [95–100]. This paper is organized as follows. To start with, in Section 2 we complete the spacetime deformation theory [82] by introducing DC complex and showing how it restores the world-deformation tensor. We also briefly revisit the theory of TSSD to make the rest of the paper understandable. An outline of the key points of TSSD theory of relevance to gauge MAG theory is stated in Section 3. The concluding remarks are presented in Section 4. The appendices discuss some relevant topics on the TSSD theory and algebraic operations in use.
2. Spacetime Deformations and Beyond: Model Building
2.1. Determination of and
2.2. TSSD: Revisited
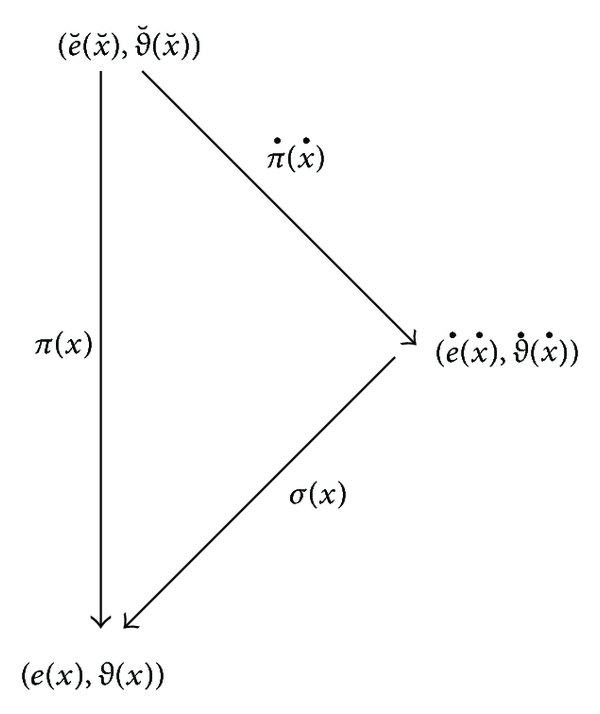
For the benefit of the reader, a brief outline of the key ideas behind the TSSD [82], as a guiding principle, is given in this section to make the rest of the paper understandable. Before we report on the physical foundation of post-Riemannian geometry, we may remark on the form of generic spacetime deformation, π(x). When torsion is nonvanishing, the affine connection is no longer coincident with the Levi-Civita connection, and the geometry is no longer Riemannian, but one has a RC spacetime, U4, with a nonsymmetric, but metric-compatible, connection. Teleparallel gravity, in turn, represented a new way of including torsion into general relativity, an alternative to the scheme provided by the usual Einstein-Cartan-Sciama-Kibble approach. However, the gravitational coupling of the fundamental fields in teleparallel gravity is a very controversial subject [15, 111–114]. The basic difficulty lies in the definition of the spin connection and consequently in the correct form of the gravitational coupling prescription. For a specific choice of the free parameters, teleparallel gravity becomes completely equivalent to GR. In this case it is usually referred to as the teleparallel equivalent of GR. From this point of view, curvature and torsion are simply alternative ways of describing the gravitational field and are consequently related to the same degrees of freedom of gravity. Teleparallel gravity attributes gravitation to torsion, but in this case torsion accounts for gravitation not by geometrizing the interaction, but by acting as a force. The fundamental difference between these two theories above was that, whereas in the former a torsion is a propagating field having as a source—the energy-momentum tensor, in the latter a torsion is not a propagating field having as a source—the total spin, a point which can be considered a drawback of this model. In fact, the two physical interpretations of torsion described above are clearly conflictive. This problem can be solved just only by experiment. Therefore, we have to separate, from the very outset, these two completely different cases. This reasoning supports our choice of a double deformation map. Namely, following [82], we assume that the spacetime deformation π(x) comprises the two ingredient deformations . Hence, local tetrad deformations (13) are performed according to the following heuristic map, in two steps (two-step deformation map):
3. Outline of the Key Points of TSSD Gauge MAG Theory
4. Concluding Remarks
The actual advantage of present approach is twofold. To complete the TSSD theory [82], at first, we build up the distortion-complex and show how it restores the world-deformation tensor, which still has been put in it by hand. In this approach we suggest to extend the SO(3,1) group of standard EC theory to local GL(4, R) group. The latter is surely not the invariance of the action of standard EC theory, and so it takes the latter into diverse other ones still invariant under spacetime diffeomorphisms. All the fundamental gravitational structures in fact, the metric as much as the coframes and connections, acquire a DC induced theoretical interpretation. Through a nontrivial choice of explicit form of a DC which we have at our disposal, we have a way to construct various generalizations and alternatives of the standard gravity. Secondly, we extend the geometrical ideas of the TSSD theory to study, in the framework of the first order Lagrangian, the physical foundation of the gauge model of more general metric-affine gravity theory with a dynamical torsion. It is remarkable that, in the framework of the first order standard Lagrangian, the equations of the standard MAG theory, in which the equation defining torsion is the algebraic type and in fact no propagation of torsion is allowed, can be equivalently replaced by the modified equations in which the torsion, in general, is dynamical. In testing the too general MAG equations (77) in some limit, we have to put on Lagrange multipliers to recover the field equation for different (sub)cases: in the case of TSSD-PG, one has to kill nonmetricity; TSSD-EC is the TSSD-PG with the curvature scalar as gravitational Lagrangian, whereas the special physical ansatz for the spacetime deformations yields the short-range propagating spin-spin interaction.
Conflict of Interests
The author declares that there is no conflict of interests regarding the publication of this paper.
Acknowledgments
The author would like to thank W.-T. Ni for drawing attention to the pseudoscalar-photon interaction theory. This paper was only made possible through substantial support of the anonymous referees whose helpful and knowledgable comments and suggestions are much appreciated.
Appendices
A. TSSD: More Details
B. Some Algebraic Operations
Since the 4D-dimensional teleparallel manifold is diffeomorphic to R4, one can choose an orientation on and restrict the frames to agree with that orientation so that only transformations with values in are allowed. The metric then defines the Hodge dual of differential forms. The following algebraic operations are defined.




