Hydraulic analysis of water distribution networks is an important problem in civil engineering. A widely used approach in steady-state analysis of water distribution networks is the global gradient algorithm (GGA). However, when the GGA is applied to solve these networks, zero flows cause a computation failure. On the other hand, there are different mathematical formulations for hydraulic analysis under pressure-driven demand and leakage simulation. This paper introduces an optimization model for the hydraulic analysis of water distribution networks using a metaheuristic method called shuffled complex evolution (SCE) algorithm. In this method, applying if-then rules in the optimization model is a simple way in handling pressure-driven demand and leakage simulation, and there is no need for an initial solution vector which must be chosen carefully in many other procedures if numerical convergence is to be achieved. The overall results indicate that the proposed method has the capability of handling various pipe networks problems without changing in model or mathematical formulation. Application of SCE in optimization model can lead to accurate solutions in pipes with zero flows. Finally, it can be concluded that the proposed method is a suitable alternative optimizer challenging other methods especially in terms of accuracy.

1. Introduction

A water distribution network is composed of an edge set consisting of pumps, pipes, valves, and a node set consisting of reservoirs and pipe intersections [1]. The equations governing the flows and heads in a water distribution system are nonlinear, and often a Newton iterative solution algorithm is used in which a linearized set of equations is solved at each iteration [2]. The Newton-based global gradient algorithm (GGA) is a popular method used in solving the water distribution System (WDS) equations [3]. Given the nonlinearity of the system of equations, the Newton-based computation of the solution involves an iterative two-step process. The first step includes computing the state variable update, which requires the solution of linear system derived from the Jacobian of the WDS equations. The second step deals with updating estimates of the state variables. The first step is typically the most computationally expensive process within the GGA [4]. Furthermore, some of the pipes in a network, in which the head losses are modeled by the Hazen-Williams formula, have zero flows. In that case, a key matrix in the method becomes singular and the matrix to be inverted becomes ill conditioned [2]. As a result a failure occurs in the computation. On the other hand, there are no options for pressure-driven demand and leakage simulation in the EPANET program. Meanwhile, there is still a chance to develop a new method for water distribution network analysis in these conditions. In this paper an optimization model is introduced for hydraulic analysis of water distribution networks using a metaheuristic algorithm called shuffled complex evolution (SCE) algorithm.

The analysis of hydraulic networks should be treated as an optimization problem, as shown by Arora [5], Hall [6], and Collins et al. [1]. Arora considered a simple two-piped loop whereas Collins et al. build the basis of their approach on rigorous theoretical background and developed nonlinear optimization models, whose solutions yielded the hydraulic network analysis [7]. In this paper the Collins model is minimized through the application of shuffled complex evolution algorithm. There is no need to solve linear systems of equations in this methodology, and handling of pressure-driven demand and leakage simulation can be done in a simple way, so an initial solution vector, which is sometimes critical to the convergence, is not required. Furthermore, the proposed model does not entail any complicated mathematical expression and operation. The Collins model is described in the following section.

2. Cocontent Model Approach

Arora [5] is the first researcher who suggested an approach based on the principle of conservation of energy. According to the principle, “Flow in the pipes of a hydraulic network adjusts so that to minimize the expenditure of the system energy.” Then, Collins et al. [1] proposed a model termed the cocontent model, which is based on equations having the unknown nodal heads as the basic unknowns, that is, based on H equations. The unknown pipe flows are expressed in terms of the nodal heads and the known pipe resistances, so that the energy loss in pipe x (E_x) is given by [7]

(1)

in which h_x is head loss in pipe x, H_i = H_oi and H_j = H_oj, for source nodes. R_k is the characteristic parameter of the pipe resistance which depends on roughness length, diameter, and unit of measurement. For example, if the Hazen-Williams equation is used, values n and R in SI units are defined as R = 10.67L/C^1.852D^4.87, n = 1.852. C, D, and L are the Hazen-Williams coefficient (depending on the pipe material), the diameter, and its length, respectively.

Now consider the network of Figure 1, with the known and unknown parameters as shown therein. Let the unknown nodal heads at nodes 1, 2, 3, 4, and 5 be H₁, H₂, H₃, H₄, and H₅, respectively. Herein also consider a ground node G with fixed known level H_0G, as shown in Figure 1. The nodes 1, 2, 3, and 5 are connected to the ground node G with pseudopipes, carrying the known nodal outflows q₁, q₂, q₃, and q₅ as shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Schematic representation of the looped pipe network with 5 unknown nodal heads.

The cocontent optimization model is expressed as

(2)

where h_L is local loss for valve and h_p is pump head.

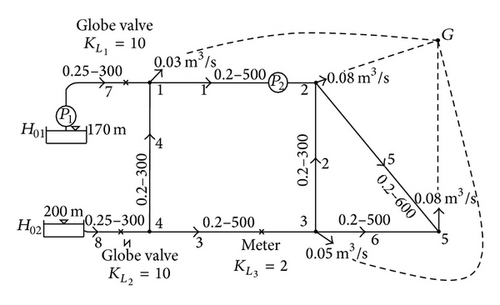
The first eight terms of the objective function represent the energy loss in real pipes 1, …, 8 of the network, respectively, and the last four terms show (1/n + 1) times the energy loss in the pseudopipes [7]. It should be noted that there are no constraints and therefore an unconstrained model in four decision variables is made. For minimization of optimization model, which is partially differentiating in unknown heads, the node-flow continuity equations are created. Therefore, the solution of the cocontent model gives the values of the unknown heads such that the node-flow continuity relationships are satisfied [7].

By partially differentiating (2) with respect to H₁, H₂, H₃, H₄, and H₅, we get

(3)

That is the purely head-based formulations of the network equations. So cocontent model not only minimizes the energy of flow but also preserves water balance in network. For simplicity, H_0G can be taken as zero. The general cocontent model can be expressed as

(4)

Collins et al. [1] suggested the solution of the NLP optimization of the model. The methods they used were (1) the Frank-Wolfe method, (2) a piecewise linear approximation, and (3) the convex simplex method, which are highly dependent on initial guesses and in some cases converge to an incorrect solution [1].

3. Head Dependent Analysis

In the common approaches, it is presumed that the nodal demands are always satisfied at all demand nodes, irrespective of the available HGL values at demand nodes [7]. But in practice, when the head at a node is insufficient, a reduction in the water flowing from the tap is expected and, at worst, the discharge that can be drafted will be zero, regardless of the actual demand [8]. There are several solutions for these conditions, in the literature. Wagner et al. [9] and Chandapillai [10] suggested a parabolic relationship between required nodal head and minimum head. Their relationships are

(5)

H^* is the required nodal head. In this situation, applying if-then rules in the optimization model is a simple way in handling the above formulation.

4. Leakage Simulation

Water losses via leakages constitute a major challenge to the effective operation of municipal WDS since they represent not only diminished revenue for utilities but also undermined service quality [11] and wasted energy resources [12]. In order to conduct a more accurate analysis of a WDS, such as a better estimate of flow through the network (with respect to both satisfied demand and losses through leakage), a hydraulic analysis capable of accounting for pressure-driven (also known as head-driven) demand and leakage flow at the pipe level should prove invaluable. To reach this goal, a leakage model is expressed as follows [13]:

(6)

where P_k is average pressure in the pipe computed as the mean of the pressure values at the end nodes i andj of the kth pipe; and l_k is length of that pipe. Variables α_k and β_k are two leakage model parameters [14]. The allocation of leakage to the two end nodes can be performed in a number of ways [15]. Here the nodal leakage flow q_j-leak is computed as the sum of q_k-leak flows of all pipes connected to node j as follows:

(7)

where P_k = (P_i + P_j)/2. This formulation also easily applies to cocontent model without any mathematical complexity. Numerical example 4 demonstrates hydraulic analysis of a real pipe network in this situations.

5. Application of Shuffled Complex Evolution Algorithm for Minimizing Cocontent Model

This study introduces the shuffled complex evolution (SCE) algorithm for the hydraulic analysis. Since the algorithm was originally developed to solve optimization problems, the hydraulic network analysis was introduced into an optimization problem (cocontent model). One advantage of the SCE algorithm is that it does not need an initial solution vector which must be chosen carefully in many other procedures if numerical convergence is to be achieved. Furthermore, application of SCE algorithm in cocontent model does not require any complicated mathematical expression and operation. In this model, pressure-driven demand and leakage can be simulated easily and there is no failure in computation in zero flow conditions.

5.1. Shuffled Complex Evolution (SCE)

Shuffled complex evolution (SCE) is a simple powerful and population-based stochastic optimization algorithm that outperforms many metaheuristic algorithms in numerical single-objective optimization problems. This method is based on a synthesis of four concepts: (1) combination of deterministic and probabilistic approaches; (2) systematic evolution of a “complex” of points spanning the parameter space, in the direction of global improvement; (3) competitive evolution; (4) complex shuffling [16]. The “complex” is similar to the genetic pool in the GA. The synthesis of these operators makes the SCE method effective and robust and also flexible and efficient [17].

In SCE method, each individual represents a feasible solution for the problem. The search within the feasible region is conducted by first dividing the set of current feasible trial solutions into several complexes, each containing equal number of trial solutions. Each complex represents a local area of the whole domain. Concurrent and independent searches within each complex are conducted until each converges to its local optimal value. Each of the complexes, which are now defined by new trial solutions, is collected into a common pool, shuffled by ranking according to their objective function value, and then further divided into new complexes. The procedure is terminated when none of the local optima found among the complexes can improve on the best current local optimum. The SCE method used the downhill simplex method to accomplish local searches. So, shuffled complex evolution tries to balance between a wide scan of a large solution space and deep search of promising locations. It depends mainly on partitioning the solution space into local communities and performing local search within these communities. Then, it shuffles these local communities to perform global search.

The steps of the procedure of SCE, as shown in Figure 2, include the following.

Step 1: initialize problem and algorithm parameters.
Step 2: samples generation.
Step 3: rank solutions.
Step 4: partition into complexes.
Step 5: start Competitive Complex Evolution (CCE).
Step 6: shuffle complexes.
Step 7: check the stopping criterion.

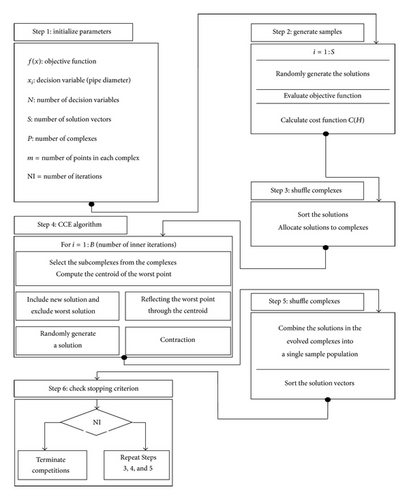
5.1.1. Step 1: Initialize the Problem and Algorithm Parameters

In Step 1, the optimization problem is specified as follows:

(8)

where C(H) is an objective function; H is the set of each decision variable. In this paper, the objective function is the cocontent model; the unknown heads are the decision variables.

5.1.2. Step 2: Samples Generation

The initial population for the DE is created arbitrarily by the following formula:

(9)

where τ denotes a uniformly distributed random value within the range [0,1]. H_min⁡(i, j) and H_max⁡(i, j) are maximum and minimum limits of variable j and node i. Then the fitness values C(H) of all the individuals of population are calculated. The position matrix of the population of generation G can be represented as

(10)

in which N is the number of unknown nodes.

5.1.3. Step 3: Rank Solutions

In this step, the s solutions are sorted in order of increasing criterion value, so that the first vector represents the smallest value of the objective function and the last vector indicates the largest value.

5.1.4. Step 4: Partition into Complexes

The s solutions are partitioned into p complexes, each containing m points. The complexes are partitioned such that the first complex contains every p(k − 1) + 1 ranked point, the second complex contains every p(k − 1) + 2 ranked point, and so on, where k = 1,2, …, m [16].

5.1.5. Step 5: Start Competitive Complex Evolution (CCE)

CCE algorithm is based on the simplex downhill search scheme and is one key component of SCE algorithm. This algorithm is presented as follows.

(1)
A subcomplex by randomly selecting q solutions from the complex according to a trapezoidal probability distribution is constructed. The probability distribution is specified such that the best solution has the highest chance of being selected to form the subcomplex and the worst point has the least chance.
(2)
The worst solution of the subcomplex is identified and the centroid of the subcomplex without including the worst solution is computed as follows:
(11)
(3)
In this step, reflection operator is used, by reflecting the worst point through the centroid according to the following formula:
(12)
If the newly generated solution is within the feasible space, go to (4); otherwise, randomly generate a point within the feasible space by Equation (9) and go to (6).
(4)
If the newly generated solution is better than the worst solution, then it is replaced by the new solution. Otherwise go to (5).
(5)
In this step, contraction operator is applied, by computing a solution halfway between the centroid and the worst point:
(13)
If the contraction solution is better than the worst solution, then it is replaced by the contraction solution. Otherwise, go to (6). This step is imported from competitive complex evolution (CCE).
(6)
A solution within the feasible space is generated randomly and the worst solution is replaced by the randomly generated solution.
(7)
Steps (2)–(6) are repeated α times and steps (1)–(7) are repeated β times.

5.1.6. Step 6: Shuffle Complexes

The solutions in the evolved complexes into a single sample population are combined and the sample population is sorted in order of increasing criterion value and is shuffled into p complexes.

5.1.7. Step 7: Check the Stopping Criterion

In this section, Steps 3, 4, and 5 are repeated until the termination criterion is satisfied.

It should be noted that the competitive complex evolution (CCE) algorithm is required for the evolution of each complex. Each point of a complex is a potential “parent” with the ability to participate in the process of reproducing offspring. A subcomplex functions like a pair of parents. Use of a stochastic scheme to construct subcomplexes allows the parameter space to be searched more thoroughly. The idea of competitiveness is introduced in forming subcomplexes where the stronger survives better and breeds healthier offspring than the weaker. Inclusion of the competitive measure expedites the search towards promising regions.

A more detailed presentation of the SCE algorithm has been given by Duan et al. [17].

6. Numerical Examples

In this section, the hydraulic analyses for several conditions in some water distribution networks are performed. All computations were executed in MATLAB programming language environment with an Intel(R) Core(TM) 2Duo CPU P8700 @ 2.53 GHz and 4.00 GB RAM. In order to demonstrate the effectiveness of SCE compared with other methods, this study proposes the use of mass balance and energy balance in the network. The average of mass and energy balance is shown by δ and it is calculated by the following formula:

(14)

For Figure 1 and (2) δ is calculated as follows:

(15)

To check the performance of the SCE for the minimization of cocontent model, in all examples, ten optimization runs were performed using different random initial solutions.

6.1. Numerical Example 1

In this part, the verification of the above mentioned model was conducted via numerical simulation based on an extremely simplified network scheme (5 nodes and 7 pipes) schematically shown in Figure 3 [18]. The pipes resistances were R₁ = 1.5625, R₂ = 50, R₃ = 100, R₄ = 12.5, R₅ = 75, R₆ = 200, and R₇ = 100, as reported in Todini [18] for this network.

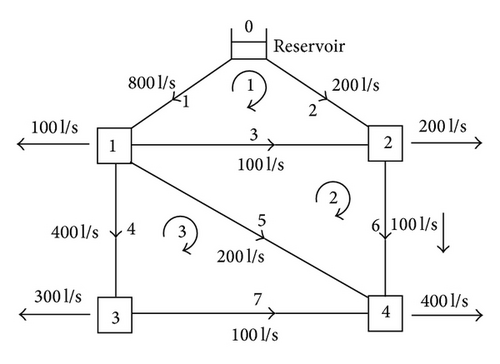
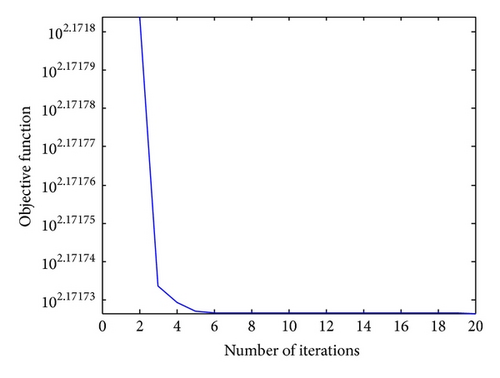
The SCE technique is applied to solve this problem according to three cases. The bound variables were set between 90 and 100 m. The problem is also solved using the global gradient algorithm (GGA) and the results are compared with those obtained by the SCE. The best, worst, and average solutions of SCE algorithm in three cases are shown in Table 1. As it can be seen in Table 1, in all cases SCE that found the optimal solution more accurately than GGA method. The average number of function evaluation is about 2000 in case 1 and about 100000 in case 3. This shows SCE can converge to global optimum rapidly but reaching high accuracy needs more operations. The convergence process of SCE algorithm has been shown in two forms in Figures 4 and 5. The absolute value of δ is calculated for each iteration in Figure 4 and the amount of objective function C(H) is calculated for each iteration in Figure 5.

Table 1. Average of mass and energy balance for numerical example 1.

SCE	δ					Average number of function evaluations
SCE		Best	Worst	Mean	Std	Average number of function evaluations
Number of complexes	4	4.60E − 08	7.06E − 07	3.04E − 07	2.30E − 07	2.03E + 03
Number of iterations in inner loop	4	4.60E − 08	7.06E − 07	3.04E − 07	2.30E − 07	2.03E + 03
Number of complexes	9	1.19E − 08	3.01E − 08	2.04E − 08	6.40E − 09	1.00E + 05
Number of iterations in inner loop	9	1.19E − 08	3.01E − 08	2.04E − 08	6.40E − 09	1.00E + 05
Number of complexes	10	1.04E − 08	4.19E − 08	2.52E − 08	8.28E − 09	1.00E + 05
Number of iterations in inner loop	15	1.04E − 08	4.19E − 08	2.52E − 08	8.28E − 09	1.00E + 05

Global gradient algorithm	Maximum accuracy		6.40E − 06

6.2. Numerical Example 2

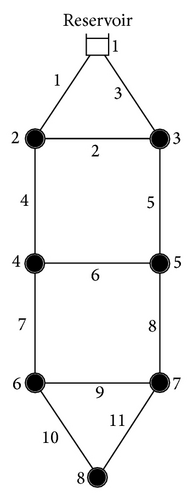
Example 2 considers the symmetric network shown in Figure 6. It has 11 pipes, seven junctions at which the head is unknown, and one fixed head node reservoir at 40 m elevation and all other nodes are at zero elevation. All pipes have diameters, D, of 250 mm and lengths, L, of 1,000 m. Node 8 has a demand of 80 l/s, and all other nodes have zero demands. In the steady state, this network has zero flows in pipes 2, 6, and 9 because of symmetry. The head loss is modeled by the Hazen-Williams equation, and each pipe has a Hazen-Williams coefficient C = 120 [2]. When the GGA is used in this network, the iterates trend toward the solution and the flows in pipes 2, 6, and 9 approach zero. As this happens, the Jacobian matrix becomes more and more badly conditioned, and the solution computed becomes ill conditioned [2]. Elhay and Simpson [2] proposed a regularization procedure for the GGA which prevents failure of the solution process provided that a flow in the network is ultimately zero or near zero.

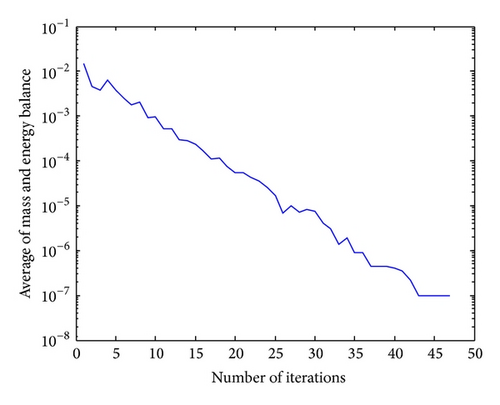
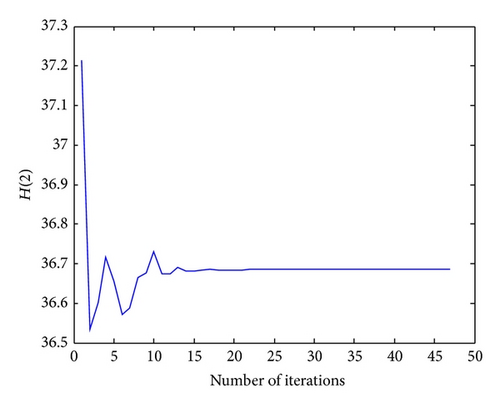
The SCE parameters are set as follows: number of decision variables = 7; number of points in each complex = 15; number of complexes for case 1 = 4, case 2 = 9, and case 3 = 10; number of iterations in inner loop for case 1 = 4, case 2 = 9, and case 3 = 15. The bound variables were set between 25 and 40 m. The previous best solution for this network, when it is simulated using the Elhay algorithm, and the average solution of SCE algorithm are shown in the second and third columns of Table 2, respectively. As can be observed in Table 2, mass and energy balance (δ) in SCE are more accurate than the Elhay algorithm. Table 3 compares the results of applying the SCE algorithm in three cases. The convergence process of SCE algorithm has been shown in two forms in Figures 7 and 8. The absolute value of δ is calculated for each iteration in Figure 7 and the value of head pressure in node 2, H(2), is calculated for each iteration in Figure 8.

Table 2. Head and parameter δ in numerical example 2.

Node number	H (m) [2]	H (m)	δ [2]	δ (SCE)
1	40	40	0	0
2	36.6813	36.6853	0	1.8E − 07
3	36.6813	36.6853	0	1.8E − 07
4	33.3626	33.3706	6.5E − 07	8.4E − 08
5	33.3626	33.3706	6.5E − 07	8.7E − 08
6	30.044	30.0559	6.5E − 07	6.7E − 08
7	30.044	30.0559	6.5E − 07	6.6E − 08
8	26.7253	26.7411	5.2E − 05	1.2E − 10

Table 3. Average of mass and energy balance for numerical example 2.

SCE	δ					Average number of function evaluations
SCE		Best	Worst	Mean	Std	Average number of function evaluations
Number of complexes	4	2.21E − 06	7.24E − 06	4.65E − 06	1.61E − 06	4.19E + 03
Number of iterations in inner loop	4	2.21E − 06	7.24E − 06	4.65E − 06	1.61E − 06	4.19E + 03
Number of complexes	9	1.05E − 06	5.35E − 06	3.46E − 06	1.51E − 06	9.29E + 03
Number of iterations in inner loop	9	1.05E − 06	5.35E − 06	3.46E − 06	1.51E − 06	9.29E + 03
Number of complexes	10	6.36E − 08	1.78E − 07	1.08E − 07	3.89E − 08	1.72E + 04
Number of iterations in inner loop	15	6.36E − 08	1.78E − 07	1.08E − 07	3.89E − 08	1.72E + 04

Global gradient algorithm	Maximum accuracy		Fail
Elhay algorithm	Maximum accuracy		7.42E − 06

6.3. Numerical Example 3

The simplified water distribution network shown in Figure 9 was used in order to demonstrate the advantages of the proposed model in pressure-driven demand condition. For the sake of simplicity, the same Hazen-Williams roughness coefficient C = 130 was assumed for all the 14 pipes of identical length of 1000 m, while no local losses have been added. The following diameters have been used in the example: 500 mm (P-2); 400 mm (P-1); 300 mm (P-4, P-7); 250 mm (P-10); 200 mm (P-3, P-5, P-6, and P-13); 150 mm (P-8, P-9, P-11, P-12, and P-14). The nodal demands are listed in the following tables together with the ground elevation Z_i. Without loss of generality, in this example, the minimum head requirement

has been assumed to be equal to the ground elevation Z_i [8]. So the relationship between the required nodal head and minimum head is

(16)

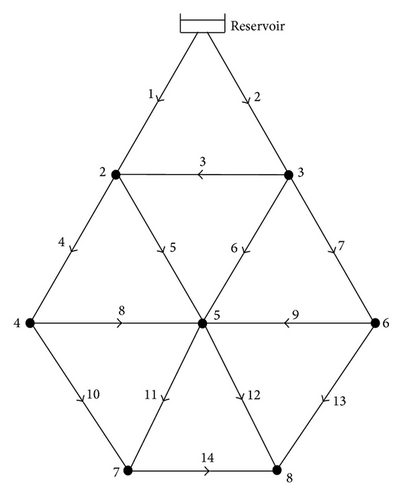
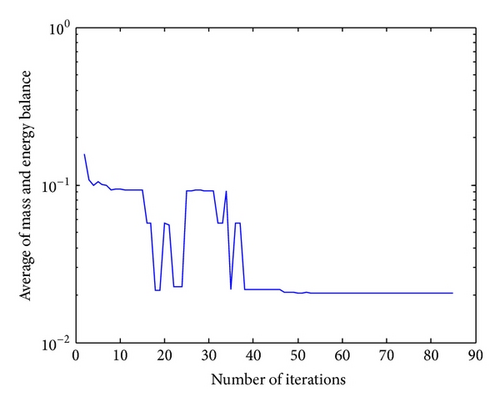
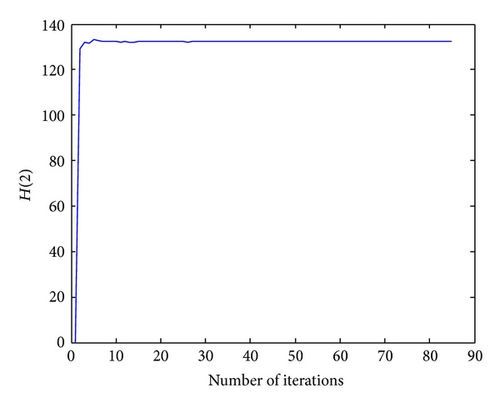
Todini [8] proposed a three-step approach for solving this network and its solution is reported in the 4th column of Table 4. In the proposed method pressure-driven model can be applied in hydraulic analysis without any mathematical formulation. In this situation, an if-then rule is added to cocontent model and optimization process is conducted. The number of decision variables in SCE algorithm is 7; the bound variables were set between 50 and 140 m. ten optimization runs were performed using different random initial solutions for all the cases and the results are illustrated in Table 5. Results confirm that SCE is more accurate compared with Todini algorithm in case 2 and case 3. In Table 4, the best result is shown in bold, and it is considered that the method of SCE has calculated the best value of δ at 5 nodes while the Todini method has done it at 2 nodes. The convergence process of SCE algorithm has been shown in two forms in Figures 10 and 11. The absolute value of δ is calculated for each iteration in Figure 10 and the value of head pressure in node 2, H(2), is calculated for each iteration in Figure 11.

Table 4. Head and parameter δ in numerical example 3.

Node number	Z (m)	SCE	3 steps	SCE	3 steps	SCE	3 steps
Node number	Z (m)	H (m)	H (m)	H − Z	H − Z	δ	δ
1	140	140	140	0	0	0	0
2	80	129.304	130.07	49.304	50.07	1.49E − 07	3.10E − 04
3	90	132.288	132.76	42.288	42.76	1.26E − 07	0.0041
4	70	109.587	110.96	39.587	40.96	2.03E − 07	0.0022
5	80	80.000	88.54	0.000	8.54	0.058	1.51E − 04
6	90	90.000	91.45	0.000	1.45	0.0069	6.02E − 04
7	90	90.000	90.00	0.000	0.00	0.080	0.1421
8	100	88.922	90.43	−11.078	−9.57	5.84E − 08	0.0439

Table 5. Average of mass and energy balance for numerical example 3.

SCE	δ					Average number of function evaluations
SCE		Best	Worst	Mean	Std	Average number of function evaluations
Number of complexes	5	3.32E − 02	7.97E − 02	5.95E − 02	1.62E − 02	4.30E + 04
Number of iterations in inner loop	5	3.32E − 02	7.97E − 02	5.95E − 02	1.62E − 02	4.30E + 04
Number of complexes	9	2.07E − 02	5.44E − 02	2.52E − 02	1.09E − 02	6.27E + 04
Number of iterations in inner loop	9	2.07E − 02	5.44E − 02	2.52E − 02	1.09E − 02	6.27E + 04
Number of complexes	10	2.07E − 02	2.07E − 02	2.07E − 02	2.17E − 08	6.04E + 04
Number of iterations in inner loop	15	2.07E − 02	2.07E − 02	2.07E − 02	2.17E − 08	6.04E + 04

Three-step approach [8]	Maximum accuracy		2.76E − 02

6.4. Numerical Example 4

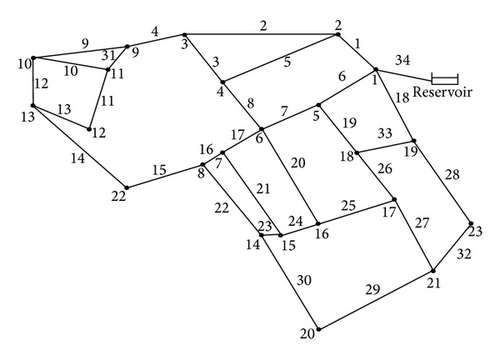
The fourth considered network is a real planned network designed for an industrial area in Apulian Town (Southern Italy). The network layout is illustrated in Figure 12 and the corresponding data are provided in Table 6. With respect to the leakages, they have been assumed to be pressure-driven (see (6)) given that they are implemented in the pressure driven network simulation model as described above [14]. The parameter β = 1.0632 × 10⁻⁷ and α = 1.2, as reported in Giustolisi et al. [14] for this network. Giustolisi et al. [14] proposed a hydraulic simulation model, which fully integrates a classic hydraulic simulation algorithm, such as that of Todini and Pilati [3] found in EPANET 2, with a pressure-driven model that entails a more realistic representation of the leakage. They applied their model in this network. The results are demonstrated in Table 7. In this table, the best result is shown in bold, and it is considered that the method of SCE has calculated the best value of δ at 14 nodes while the Gistulishi method has done it at 9 nodes. In the proposed method, there is no need to modify the mathematical formulation for hydraulic analysis. An if-then rule is added to cocontent model and the optimization process is performed easily. As you can see in Table 8, SCE found the optimal solution more accurately than the Giustolisi algorithm. The convergence process of SCE algorithm has been shown in two forms in Figures 4 and 5. The absolute value of δ is calculated for each iteration in Figure 13 and the amount of head pressure in node 20, H(20), is calculated for each iteration in Figure 14.

Table 6. Hydraulic data relevant to numerical example 4.

Pipe number	L (m)	D (mm)
1	348.5	327
2	955.7	290
3	483	100
4	400.7	290
5	791.9	100
6	404.4	368
7	390.6	327
8	482.3	100
9	934.4	100
10	431.3	184
11	513.1	100
12	428.4	184
13	419	100
14	1023.1	100
15	455.1	164
16	182.6	290
17	221.3	290
18	583.9	164
19	452	229
20	794.7	100
21	717.7	100
22	655.6	258
23	165.5	100
24	252.1	100
25	331.5	100
26	500	204
27	579.9	164
28	842.8	100
29	792.6	100
30	846.3	184
31	164	258
32	427.9	100
33	379.2	100
34	158.2	368

Table 7. Head and parameter δ in numerical example 4.

Node number	q (l/s)	H (m) (Giustolisi algorithm)	H (m)	δ (Giustolisi algorithm)	δ (SCE)
1	10.863	26.9	33.29	0.154743	0.004738
2	17.034	24.81	31.83	0.02131	0.006532
3	14.947	21.3	27.39	0.059002	0.005364
4	14.28	17.22	25.34	0.001257	0.005033
5	10.133	23.54	30.89	0.026184	0.004018
6	15.35	20.1	29.02	0.030898	0.005399
7	9.114	18.91	27.94	0.017147	0.003087
8	10.51	17.9	27.34	0.00227	0.003545
9	12.182	17.85	26.35	0.002936	0.003867
10	14.579	12.66	23.24	0.008277	0.004362
11	9.007	16.23	25.95	0.031554	0.002723
12	7.575	10.12	22.05	0.002732	0.002138
13	15.2	10.03	22.45	0.0126	0.004328
14	13.55	15.41	25.95	0.001318	0.004352
15	9.226	14	24.17	0.002199	0.002934
16	11.2	14.36	24.05	0.007089	0.003586
17	11.469	15.3	25.42	0.000103	0.00361
18	10.818	18.83	28.38	0.011889	0.003908
19	14.675	19.35	28.39	5.43E − 05	0.005097
20	13.318	10.01	23.79	0.013059	0.003974
21	14.631	11.48	22.35	0.003276	0.004141
22	12.012	14	25.46	0.003901	0.003677
23	10.326	10.45	20.11	0.002551	0.002979
24	—	36.45	36.45	—	—

Table 8. Average of mass and energy balance for numerical example 4.

SCE	δ					Average number of function evaluations
SCE		Best	Worst	Mean	Std	Average number of function evaluations
Number of complexes	5	4.00E − 03	4.50E − 02	4.10E − 03	2.75E − 04	6.59E + 04
Number of iterations in inner loop	5	4.00E − 03	4.50E − 02	4.10E − 03	2.75E − 04	6.59E + 04
Number of complexes	9	3.90E − 03	4.15E − 03	4.00E − 03	3.96E − 05	1.15E + 05
Number of iterations in inner loop	9	3.90E − 03	4.15E − 03	4.00E − 03	3.96E − 05	1.15E + 05
Number of complexes	10	3.70E − 03	4.10E − 03	3.90E − 03	2.53E − 05	1.19E + 05
Number of iterations in inner loop	15	3.70E − 03	4.10E − 03	3.90E − 03	2.53E − 05	1.19E + 05

Giustolisi algorithm	Maximum accuracy		1.81E − 02

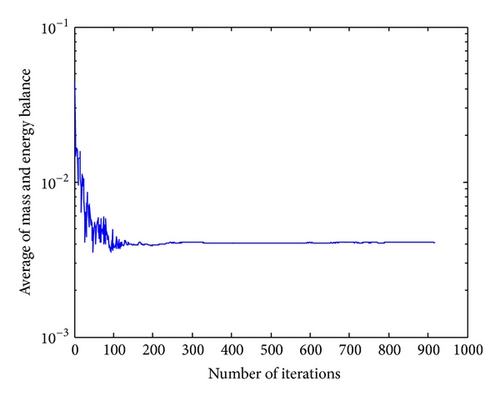
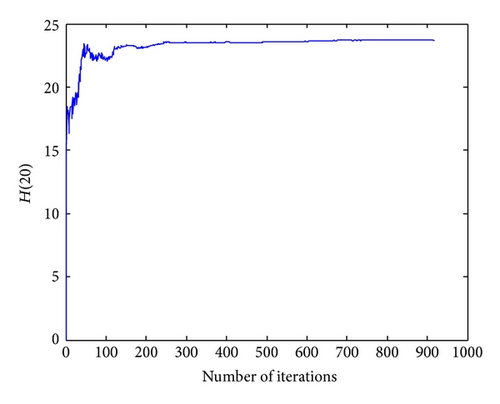
In general, 4 different pipe networks were considered in this paper and different mathematical formulations were used for the hydraulic analysis of these networks. However, the overall results indicate that the proposed method has the capability of handling various pipe networks problems with no change in the model or mathematical formulation. Application of SCE in cocontent model can result in finding accurate solutions in pipes with zero flows and the pressure-driven demand and leakage simulation can be solved through applying if-then rules in cocontent model. As a result, it can be concluded that the proposed method is a suitable alternative optimizer, challenging other methods especially in terms of accuracy.

7. Conclusions

The objective of the present paper was to provide an innovative approach in the analysis of the water distribution networks based on the optimization model. The cocontent model is minimized using shuffled complex evolution (SCE) algorithm. The methodology is illustrated here using four networks with different layouts. The results reveal that the proposed method has the capability to handle various pipe networks problems without changing in model or mathematical formulation. The advantage of the proposed method lies in the fact that there is no need to solve linear systems of equations, pressure-driven demand and leakage simulation are handled in a simple way, accurate solutions can be found in pipes with zero flows, and it does not need an initial solution vector which must be chosen carefully in many other procedures if numerical convergence is to be achieved. Furthermore, the proposed model does not require any complicated mathematical expression and operation. Finally, it can be concluded that the proposed method is a viable alternative optimizer that challenges other methods particularly in view of accuracy.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

References

1 Collins M., Cooper L., Helgason R., Kenningston J., and LeBlanc L., Solving the pipe network analysis problem using optimization techniques, Management Science. (1978) 24, no. 7, 747–760, https://doi.org/10.1287/mnsc.24.7.747.
10.1287/mnsc.24.7.747
Web of Science® Google Scholar
2 Elhay S. and Simpson A. R., Dealing with zero flows in solving the nonlinear equations for water distribution systems, Journal of Hydraulic Engineering. (2011) 137, no. 10, 1216–1224, 2-s2.0-80155196721, https://doi.org/10.1061/(ASCE)HY.1943-7900.0000411.
10.1061/(ASCE)HY.1943-7900.0000411
Google Scholar
3 Todini E. and Pilati S., A gradient algorithm for the analysis of pipe networks, Computer Applications in Water Supply, 1988, 1, John Wiley & Sons, London, UK, 1–20, System Analysis and Simulation.
Google Scholar
4 Zecchin A. C., Thum P., Simpson A. R., and Tischendorf C., Steady-state behaviour of large water distribution systems: the algebraic multigrid method for the fast solution of the linear step, Journal of Water Resources Planning and Management. (2012) 138, no. 6, 639–650.
10.1061/(ASCE)WR.1943-5452.0000226
Web of Science® Google Scholar
5 Arora M. L., Flow split in closed loops expending least energy, Journal of the Hydraulics Division. (1976) 102, 455–458, 2-s2.0-0016889280.
10.1061/JYCEAJ.0004520
Google Scholar
6 Hall M. A., Hydraulic network analysis using (generalized) geometric programming, Networks. (1976) 6, no. 2, 105–130, 2-s2.0-0016947395.
10.1002/net.3230060204
Google Scholar
7 Bhave P. R. and Gupta R., Analysis of water distribution networks, Alpha Science International, Technology & Engineering, 2006.
Google Scholar
8 Todini E., A More Realistic Approach to the “Extended Period Simulation” of Water Distribution Networks, 2003, no. chapter 19, Taylor & Francis, London, UK, Advances in Water Supply Management.
10.1201/NOE9058096081.ch19
Google Scholar
9 Wagner J. M., Shamir U., and Marks D. H., Water distribution reliability: analytical methods, Journal of Water Resources Planning and Management. (1988) 114, no. 3, 253–275, 2-s2.0-0024011404.
10.1061/(ASCE)0733-9496(1988)114:3(253)
Web of Science® Google Scholar
10 Chandapillai J., Realistic simulation of water distribution system, Journal of Transportation Engineering. (1991) 117, no. 2, 258–263, 2-s2.0-0026131120.
10.1061/(ASCE)0733-947X(1991)117:2(258)
Google Scholar
11 Almandoz J., Cabrera E., Arregui F., CabreraE.Jr., and Cobacho R., Leakage assessment through water distribution network simulation, Journal of Water Resources Planning and Management. (2005) 131, no. 6, 458–466, 2-s2.0-27544482565, https://doi.org/10.1061/(ASCE)0733-9496(2005)131:6(458).
10.1061/(ASCE)0733-9496(2005)131:6(458)
Web of Science® Google Scholar
12 Colombo A. F. and Karney B. W., Energy and costs of leaky pipes toward comprehensive picture, Journal of Water Resources Planning and Management. (2002) 128, no. 6, 441–450, 2-s2.0-0036842573, https://doi.org/10.1061/(ASCE)0733-9496(2002)128:6(441).
10.1061/(ASCE)0733-9496(2002)128:6(441)
Web of Science® Google Scholar
13 Germanopoulos G., A technical note on the inclusion of pressure dependent demand and leakage terms in water supply network models, Civil Engineering Systems. (1985) 2, no. 3, 171–179, 2-s2.0-0022117480.
10.1080/02630258508970401
Google Scholar
14 Giustolisi O., Savic D., and Kapelan Z., Pressure-driven demand and leakage simulation for water distribution networks, Journal of Hydraulic Engineering. (2008) 134, no. 5, 626–635, 2-s2.0-42449093808, https://doi.org/10.1061/(ASCE)0733-9429(2008)134:5(626).
10.1061/(ASCE)0733-9429(2008)134:5(626)
Web of Science® Google Scholar
15 Ainola L., Koppel T., Tiiter K., and Vassiljev A., Water network model calibration based on grouping pipes with similar leakage and roughness estimates, Proceedings of the Joint Conference on Water Resource Engineering and Water Resources Planning and Management (EWRI ′00), August 2000, Minneapolis, Minn, USA, 1–9, 2-s2.0-74949124036, https://doi.org/10.1061/40517(2000)197.
10.1061/40517(2000)197
Google Scholar
16 Duan Q., Sorooshian S., and Gupta V. K., Optimal use of the SCE-UA global optimization method for calibrating watershed models, Journal of Hydrology. (1994) 158, no. 3-4, 265–284, 2-s2.0-0028449781.
10.1016/0022-1694(94)90057-4
Web of Science® Google Scholar
17 Duan Q. Y., Sorooshian S., and Gupta V. K., Shuffled complex evolution approach for effective and efficient global minimization, Journal of Optimization Theory and Applications. (1993) 76, no. 3, 501–521, 2-s2.0-0027558431, https://doi.org/10.1007/BF00939380.
10.1007/BF00939380
Web of Science® Google Scholar
18 Todini E., On the convergence properties of the different pipe network algorithms, Proceedings of the Annual Water Distribution Systems Analysis Symposium (ASCE ′06), August 2006, 1–16, 2-s2.0-40549127016, https://doi.org/10.1061/40941(247)75.
10.1061/40941(247)75
Google Scholar

Citing Literature

All articles

Hydraulic Analysis of Water Distribution Network Using Shuffled Complex Evolution

Abstract

1. Introduction

2. Cocontent Model Approach

3. Head Dependent Analysis

4. Leakage Simulation