Discrete Dynamics in Nature and Society
Volume 2014, Issue 1 920410
Research Article
Open Access

Global Period-Doubling Bifurcation of Quadratic Fractional Second Order Difference Equation

Senada Kalabušić, 

Senada Kalabušić

Department of Mathematics, University of Sarajevo, 71000 Sarajevo, Bosnia and Herzegovina unsa.ba

Search for more papers by this author
M. R. S. Kulenović, 

Corresponding Author

M. R. S. Kulenović

Department of Mathematics, University of Rhode Island, Kingston, RI 02881, USA uri.edu

Search for more papers by this author
M. Mehuljić, 

M. Mehuljić

Division of Mathematics, Faculty of Mechanical Engineering, University of Sarajevo, 71000 Sarajevo, Bosnia and Herzegovina unsa.ba

Search for more papers by this author
First published: 27 April 2014
https://doi.org/10.1155/2014/920410
Citations: 9
Academic Editor: Raghib Abu-Saris

Abstract

We investigate the local stability and the global asymptotic stability of the difference equation , n = 0,1, … with nonnegative parameters and initial conditions such that , for all n ≥ 0. We obtain the local stability of the equilibrium for all values of parameters and give some global asymptotic stability results for some values of the parameters. We also obtain global dynamics in the special case, where β = B = 0, in which case we show that such equation exhibits a global period doubling bifurcation.

1. Introduction

In this paper, we investigate local stability and global dynamics of the following difference equation:
()
where
()
and where the initial conditions x−1 and x0 are arbitrary nonnegative real numbers such that , for all n ≥ 0. Special cases of (1), such as the cases when α = A = 0 or γ = C = 0 or β = γ = C = 0 or α = γ = C = 0, were considered in the monograph [1] and in several papers [2–5]. Equation (1) is the special case of a general second order quadratic fractional equation of the form
()
with nonnegative parameters and initial conditions such that A + B + C > 0,  a + b + c + d + e + f > 0, and , n = 0,1, …. Several global asymptotic results for some special cases of (3) were obtained in [6–9].
The change of variable xn = 1/un transforms (1) to the difference equation
()
where we assume that α + β + γ > 0 and that the nonnegative initial conditions u−1 and u0 are such that , for all n ≥ 0. Thus, the results of this paper extend to (4).

First systematic study of global dynamics of a special quadratic fractional case of (3) where A = C = D = a = c = d = 0 was performed in [2, 3]. Dynamics of some related quadratic fractional difference equations was considered in the papers [6–9]. In this paper, we will perform the local stability analysis of the unique equilibrium which is quite elaborate and we will give the necessary and sufficient conditions for the equilibrium to be locally asymptotically stable, a saddle point, or a nonhyperbolic equilibrium. The local stability analysis indicates that some possible dynamics scenarios for (1) include period-doubling bifurcations and global attractivity of the equilibrium. Another possible scenario includes global periodicity; that is, the possibility that all solutions are periodic of the same period. This means that the techniques we used in [5, 6, 10–14] are applicable. We will also obtain the global asymptotic stability results for (1). As we have seen in [1], an efficient way of studying the dynamics of (1) is considering the dynamics of 49 special cases of (1) which are obtained when one or more coefficients are set to be zero. It is interesting to notice that sometimes the most complex dynamics can be one of the very special cases of general equation, see [1]. Based on our results in [1], it is difficult to prove global asymptotic stability results of the unique equilibrium even for linear fractional difference equations where there are still two remaining cases needed to prove the general conjecture that local stability of the unique equilibrium implies the global stability. This task is even more challenging in the case of quadratic fractional difference equation such as (3).

Some interesting special cases of (1) which were thoroughly studied in [1] are the following equations.
  • (1)

    Beverton-Holt difference equation, when α = γ = A = 0:

    ()

  •  

    which represents the basic discrete model in population dynamics; see [15].

  • (2)

    Riccati difference equation, when α = A = 0:

    ()

  • (3)

    Difference equation studied in [1, 4, 16], when γ = C = 0:

    ()

  •  

    which represents the discretization of the differential equation model in biochemical networks; see [17].

The paper is organized as follows. The next section gives the preliminary results on global stability of general quadratic fractional difference equation (3) which are applicable to some special cases of (1). This section contains also a global period-doubling bifurcation result from [12], which is applicable to one special case of (1), for which we obtain the global dynamics. The third section gives local stability result for (1) for all parametric values. The fourth section gives global asymptotic stability results for several special cases of (1). Finally, the fifth section gives global dynamics for difference equation
()
where all parameters are positive, which exhibits the global period-doubling bifurcation. We pose a conjecture about global asymptotic stability of the equilibrium solutions of (8) in certain region of parameters.

2. Preliminaries

The global attractivity results obtained specifically for complicated cases of (3) are the following theorems [18].

Theorem 1. Assume that (3) has the unique equilibrium . If the following condition holds:

()
where L and U are lower and upper bounds of all solutions of (3) and L + f > 0, then is globally asymptotically stable.

Theorem 2. Assume that (3) has the unique equilibrium , where and are lower and upper bounds of specific solution of (3) and m + f > 0. If the following condition holds:

()
then is globally asymptotically stable on the interval [m, M].

In the case of (1), Theorems 1 and 2 give the following special results.

Corollary 3. If the following condition holds:

()
where L > 0 and U are lower and upper bounds of all solutions of (1), then is globally asymptotically stable.

Corollary 4. If the following condition holds:

()
where and are lower and upper bounds of specific solution of (1), then the unique equilibrium is globally asymptotically stable on the interval [m, M].

Corollary 3 can be used efficiently to obtain global stability results for the special cases of (1), in particular, for some equations of types (2,2), (3,2), and (3,3), where type (k, m) means that special case of (1) has k terms in the numerator and m terms in the denominator. See Section 4.

In this paper, we present the local stability analysis for the unique equilibrium of (1) and then we apply Corollaries 3 and 4 to some special cases of (1) to obtain global asymptotic stability results for those equations. The obtained results will give the regions of parametric space where the unique positive equilibrium of (1) is globally asymptotically stable. In the coming manuscript we will give more precise dynamics in some special cases of (1) such as the case where α = β = 0, where the theory of monotone maps will give the global dynamics.

Our results on period-doubling bifurcation will be based on the following theorem for a general second order difference equation in [19]:
()

Theorem 5. Let I be a set of real numbers and let f : I × I → I be a function which is nonincreasing in the first variable and nondecreasing in the second variable. Then, for every solution of the equation

()
the subsequences and of even and odd terms of the solution do exactly one of the following:
  • (i)

    eventually, they are both monotonically increasing;

  • (ii)

    eventually, they are both monotonically decreasing;

  • (iii)

    one of them is monotonically increasing and the other is monotonically decreasing.

The consequence of Theorem 5 is that every bounded solution of (14) converges to either equilibrium or period-two solution or to the point on the boundary, and the most important question becomes determining the basins of attraction of these solutions as well as the unbounded solutions.

The next result is the global period-doubling bifurcation result from [5] which also gives precise description of the basins of attraction of equilibrium points and periodic solutions of the considered equation.

Theorem 6. Let 𝒜 be a connected subset of ℝk, and, for each α ∈ 𝒜, let ℐα⊂ℝ be an interval. Let Γ:𝒜 → ℝ be a continuous function. Consider a family of difference equations

()

with fα(x, y) being continuous on ℛα : = ℐα × ℐα, for α ∈ 𝒜. Suppose that, for each α ∈ 𝒜, the following statements are true.

  • (a1)

    , and fα(x, y) is strictly decreasing in x and strictly increasing in y in .

  • (a2)

    There exists a family of isolated equilibria that vary continuously in α.

  • (a3)

    fα(x, y) is continuously differentiable on a neighborhood of , with partial derivatives D1fα and D2fα being continuous in α.

  • (a4)

    Let ηα and να be the roots of the characteristic equation of (15) at xα, ordered so that  |ηα | ≤|να|:

    •  

      (i) if Γ(α) < 0, then −1 < να < 0 < ηα < 1,

    •  

      (ii) if Γ(α) = 0, then −1 = να < 0 < ηα < 1,

    •  

      (iii) if Γ(α) > 0, then να < −1 < 0 < ηα < 1.

  • (a5)

    If Γ(α) < 0, xα is the unique equilibrium of (15) in ℐα and there are no prime period-two solutions in the rectangle of initial conditions ℐα × ℐα. If Γ(α) > 0, there exist no prime period-two solutions in the region of initial conditions , where Q1(a, a)  (resp.,  Q3(a, a)) denotes the first (resp., third) quadrant with respect to the point (a, a).

  • (a6)

    For Γ(α) < 0, statement A7 of Theorem 4.1 in [12] is true for the map defined on ℛα, where Fα(u, v) = (v, fα(v, u)).

Then the following statements are true.

  • (i)

    For α such that Γ(α) < 0, the equilibrium is a global attractor on ℛα.

  • (ii)

    For α such that Γ(α) > 0, the stable set of the equilibrium is a curve in ℐα × ℐα which is the graph of a continuous and increasing function that passes through and that has endpoints in ∂(ℐα × ℐα). Furthermore,

    •  

      (ii.1) if ℛα is compact or if there exists a compact set 𝒦 ⊂ ℐα such that f(ℐα × ℐα) ⊂ 𝒦, then there exist prime period-two solutions (ϕ, ψ) and (ψ, ϕ);

    •  

      (ii.2) if prime period two solutions (ϕ, ψ) and (ψ, ϕ) exist in and , respectively, and if they are the only prime period-two solutions there, then every solution {xn} with initial condition in the complement of the stable set of the equilibrium is attracted to one of the period-two solutions; that is, whenever , either x2n → ϕ and x2n+1 → ψ or x2n → ψ and x2n+1 → ϕ;

    •  

      (ii.3) if there are no prime period-two solutions, then every solution {xn} of equation xn+1 = fα(xn, xn−1),   n = 0,1, … with initial condition in 𝒲− is such that the subsequence {x2n} eventually leaves any given compact subset of ℐα, and every solution {xn} of xn+1 = fα(xn, xn−1),   n = 0,1, … with initial condition in 𝒲+ is such that the subsequence {x2n+1} eventually leaves any given compact subset of ℐα.

3. Linearized Stability Analysis

In this section we present the local stability of the unique positive equilibrium of (1).

3.1. Equilibrium Points

In view of the above restriction on the initial conditions of (1), the equilibrium points of (1) are the positive solutions of the equation:
()
or, equivalently,
()
When
()
the unique positive equilibrium of (17) is given by
()
When
()
the unique positive equilibrium of (17) is given by
()
Finally, when
()
then the only equilibrium point of (17) is the positive solution
()
of the quadratic equation (17).

In summary, it is interesting to observe that when (1) has a positive equilibrium , then is unique and satisfies (17). This observation simplifies the investigation of the local stability of the positive equilibrium of (1).

3.2. Local Stability of the Positive Equilibrium

Now we investigate the stability of the positive equilibrium of (1). Set
()
and observe that
()
If denotes an equilibrium point of (1), then the linearized equation associated with (1) about the equilibrium point is
()
where
()

Theorem 7. Assume that

()
Then, the unique equilibrium point
()
of (1) is
  • (i)

    locally asymptotically stable, if A(3C + α) + B(C + 3α + β) > βA;

  • (ii)

    a saddle point, if A(3C + α) + B(C + 3α + β) < βA;

  • (iii)

    a nonhyperbolic point, if A(3C + α) + B(C + 3α + β) = βA or (β = 0, A = 0, B > 0, α > 0).

Proof. It is easy to see that

()
Then, the proof follows from Theorem 1.1.1 in [1] and the fact that
()

Theorem 8. Assume that

()
Then, the unique equilibrium point of (1) is locally asymptotically stable.

Proof. A straightforward calculation gives

()
Then, the proof follows from Theorem 1.1.1 in [1] and the fact that
()

We have previously mentioned that if
()
then the unique positive equilibrium of (17) is the positive solution
()
of (17).
By using the identity
()
we can see that
()
()
()
()
Let
()
Set
()
It is clear that and that
()
while
()
for some ρ, σ ∈ [0, ∞). A straightforward computation gives us that
()

Lemma 9. Let p and q be the partial derivatives given by (38) and (39). Assume that

()
Then, 1 − p − q > 0 holds for all values of parameters.

Proof. The inequality 1 − p − q > 0 is equivalent to

()
which is equivalent to
()
Since
()
we have that 1 − p − q > 0 is always true.

Lemma 10. Let p and q be partial derivatives given by (38) and (39). Assume that

()
Then, p − q + 1 > 0, if and only if
()

Proof.

  • (i)

    Let A = 0, then, from (40), p − q + 1 > 0.

  • (ii)

    Assume that B(C + 3α + β) + A(C + α − β) > 0 and A > 0. Then p − q + 1 > 0 is equivalent to . One can see that

    ()

  •  

    if and only if

    ()

  •  

    since

    ()

  •  

    In view of (42), we have that p − q + 1 > 0, if and only if

    ()

  •  

    which is equivalent to

    ()

  •  

    in view of

    ()
    ()

  •  

    The conditions in (57) are equivalent to

    ()

  •  

    and from which the proof follows.

  • (iii)

    Assume that B(C + 3α + β) + A(C + α − β) < 0 and A > 0. Then p − q + 1 > 0 is equivalent to . It is easy to see that

    ()

  •  

    if and only if

    ()

  •  

    which implies that p − q + 1 > 0, if and only if

    ()

  •  

    which is equivalent to

    ()

  •  

    since

    ()

  •  

    Since

    ()

  •  

    we have that (64) is equivalent to

    ()

  •  

    and from which the proof follows.

  • (iv)

    If B(C + 3α + β) + A(C + α − β) = 0 and A > 0, then it is enough to see that

    ()

  •  

    which is equivalent in this case to

    ()

Lemma 11. Let q be the partial derivative given by (39). Assume that

()
Then, q + 1 > 0 holds for all values of parameters.

Proof. Inequality q > −1 is equivalent to

()
If C ≥ α, then, from (41), we have that q > −1.

Let C < α.

Relation (71) is equivalent to

()
or
()
It can be shown that
()
Since
()
we have that F(ρ3) < 0, if and only if γ < C(α + β)/(A + B), from which it follows that (73) is equivalent to
()
In view of (76), we have that (72) and (73) are equivalent to γ > 0.

So, q + 1 > 0 holds for all values of parameters.

Thus, we proved the following result.

Theorem 12. Assume that

()
Then, the unique equilibrium point
()
of (1) is
  • (i)

    a locally asymptotically stable point, if and only if any of the following holds:

    •  

      (a)

      ()

    •  

      (b)

      ()

  • (ii)

    a saddle point, if and only if the following holds:

    ()

  • (iii)

    a nonhyperbolic point, if and only if the following holds:

    ()

Proof. The proof follows from Theorem 1.1.1 in [1] and Lemmas 9, 10, and 11.

4. Global Asymptotic Stability Results

In this section we give the following global asymptotic stability result for some special cases of (1).

Theorem 13. (i) Consider (1), where C = 0 and all other coefficients are positive, subject to the condition

()
where L = min⁡{α, β, γ}/max⁡{A, B} and U = max⁡{α, β}/min⁡{A, B} + (γ/BL). Then is globally asymptotically stable.

(ii) Consider (1), where all coefficients are positive, subject to the condition (1) where L = min⁡{α, β, γ}/max⁡{A, B, C} and U = max⁡{α, β, γ}/min⁡{A, B, C}. Then is globally asymptotically stable.

Proof. In view of Corollary 3, we need to find the lower and upper bounds for all solutions of (1), for n ≥ 1.

  • (i)

    In this case, the lower and upper bounds for all solutions of (1), for n ≥ 1, are derived as

    ()

  • (ii)

    In this case, the lower and upper bounds for all solutions of (1), for n ≥ 1, are derived as

    ()

A consequence of Theorem 13 is the following result.

Corollary 14. Consider (1), where A = C = 0 and all other coefficients are positive, subject to the condition

()
where L = min⁡{α, β, γ}/B, U = max⁡{α, β}/B + (γ/BL). Then, is globally asymptotically stable.

By using similar method as in the proof of Theorem 13, one can prove the following result.

Theorem 15. Consider (1), where B = β = 0 and all other coefficients are positive, subject to the condition

()
where L = min⁡{α, γ}/max⁡{A, C}, U = max⁡{α, γ}/min⁡{A, C}. Then is globally asymptotically stable.

Proof. Now, we have

()

Remark 16. Equation (1), where C = γ = 0 and all other coefficients are positive reduces to well-known equation (7) which was studied in great details in [1, 4] and for which we have shown that the unique equilibrium is globally asymptotically stable, if and only if it is locally asymptotically stable; that is, if and only if the condition (i) of Theorem 7 holds. This result is certainly better than the global asymptotic result we derive from Corollaries 3 and 4. However, the results where local stability implies global stability are very rare and it seems to be limited only to second order linear fractional difference equations; see [16, 19].

Remark 17. Equation (1), where either A = 0 or B = 0 and all other coefficients are positive can be treated with Corollary 4 and global asymptotic stability of the equilibrium (whenever it exists) follows from condition (12) in the interval when , that is, when x−1x0 > 0. Similarly, (1), where exactly one of the coefficients α, β, or γ is zero, and all other coefficients are positive can be treated with Corollary 4 and global asymptotic stability of the equilibrium follows from condition (12) in the interval when , that is, when x−1x0 > 0. In this case can be replaced by U = max⁡{α, β, γ}/min⁡{A, B, C}.

5. Equation

In this section we present the global dynamics of (8), which exhibits a global period-doubling bifurcation introduced in [5].

5.1. Local Stability Analysis

Equation (8), by the change of variables
()
reduces to the equation
()
where we left the old labels γ and C for the parameters and x for variable. Equation (90) has the unique positive equilibrium given by
()
The partial derivatives associated to (90) at the equilibrium are
()
The characteristic equation associated to (90) at the equilibrium point is
()
which implies
()
By applying the linearized stability Theorem 12, we obtain the following result.

Theorem 18. The unique positive equilibrium point of (90) is

  • (i)

    locally asymptotically stable, when

    ()

  • (ii)

    a saddle point, when

    ()

  • (iii)

    a nonhyperbolic point, when

    ()

Lemma 19. If

()
then (90) possesses the unique minimal period-two solution {P(ϕ, ψ), Q(ψ, ϕ)}∈ where the values ϕ and ψ are the (positive and distinct) solutions of the quadratic equation
()
where
()

Proof. Assume that {(ϕ, ψ), (ψ, ϕ)} is a minimal period-two solution of (90). Then

()
which is equivalent to
()
which is true, if and only if ϕ ≠ ψ,
()
()
By subtracting (103) and (104), we get
()
By dividing (103) by ϕ ≠ 0 and (104) by ψ ≠ 0 and subtracting them and by using the fact that ψ ≠ ϕ, we get
()
If we set
()
where x, y > 0, then ϕ and ψ are positive and different solutions of the quadratic equation
()
In addition to condition x, y > 0, it is necessary that x2 − 4y > 0.

From (105) and (106), we obtain the system

()

We obtain that solutions (x±,  y±) of system (109) are

()
Since y− < 0, there is only one positive solution {x+, y+} of system (109). We have that x+, y+, and , if and only if
()
Therefore, there is only one minimal period-two solution {P(ϕ, ψ), Q(ψ, ϕ)} of (90) which is solution of equation
()
where
()
It is easy to see that
()
So, {P(ϕ, ψ), Q(ψ, ϕ)}∈. It can be shown that K > 0. Namely, if we consider K as a function of γ, then
()
always, because
()

5.2. Global Results and Basins of Attraction

In this section, we present global dynamics results for (90), in case C < γ.

Lemma 20. Every solution of (90) is bounded from above and from below by positive constants.

Proof. Indeed

()

Theorem 21. The following statements are true.

  • (i)

    If C < γ < (1/4)(3 + 10C + 3C2), then (90) has a unique equilibrium point , which is locally asymptotically stable and has no minimal period-two solution. Furthermore, the unique positive equilibrium point

    ()

  •  

    is globally asymptotically stable.

  • (ii)

    If γ > (1/4)(3 + 10C + 3C2), then (90) has a unique equilibrium point which is a saddle point and has the minimal period-two solution {P(ϕ, ψ), Q(ψ, ϕ)}. Global stable manifold 𝒲s(E), which is continuous increasing curve, divides the first quadrant such that the following holds:

    •  

      (ii1) every initial point (u0, v0) in 𝒲s(E) is attracted to E;

    •  

      (ii2) if (u0, v0) ∈ 𝒲+(E)  (the  region  below  𝒲s(E)), then the subsequence of even-indexed terms {(u2n, v2n)} is attracted to Q and the subsequence of odd-indexed terms {(u2n+1, v2n+1)} is attracted to P;

    •  

      (ii3) if (u0, v0) ∈ 𝒲−(E)  (the  region  above  𝒲s(E)), then the subsequence of even-indexed terms {(u2n, v2n)} is attracted to P and the subsequence of odd-indexed terms {(u2n+1, v2n+1)} is attracted to Q.

  • (iii)

    If γ = (1/4)(3 + 10C + 3C2), then (90) has a unique equilibrium point which is nonhyperbolic and has no minimal period-two solution. The equilibrium point is a global attractor.

Proof. Let

()
  • (i)

    If C < γ < (1/4)(3 + 10C + 3C2), then appropriate function of (90) is nonincreasing in the first variable and nondecreasing in the second variable. From Theorem 18, (90) has a unique equilibrium point , which is locally asymptotically stable and, from Lemma 19, (90) has no minimal period-two solution. All conditions of Theorem 6 are satisfied from which follows that a unique equilibrium point is a global attractor. So, is globally asymptotically stable.

  • (ii)

    From Theorem 18, (90) has a unique equilibrium point , which is a saddle point. From Lemma 19, (90) has a unique minimal period-two solution {P(ϕ, ψ), Q(ψ, ϕ)}. The map T = T(x, y) = (y, f(y, x)) has neither fixed points nor periodic points of minimal period-two in . All conditions of Theorem 6 are satisfied from which follows that every solution {xn}  with initial condition in the complement of the stable set of the equilibrium is attracted to one of the period-two solutions. That is, whenever , either x2n → ϕ and x2n+1 → ψ or x2n → ψ and x2n+1 → ϕ. It is not hard to see that the map T is anticompetitive (which means that T2 is competitive) and T2 is strongly competitive from which we have that conclusions (ii1), (ii2), and (ii3) hold.

  • (iii)

    The proof follows from Theorem 5 and Lemmas 19 and 20.

For graphical illustration of Theorem 21, see Figure 1.

Details are in the caption following the image
Figure 1 (a)
Open in figure viewerPowerPoint
Visual illustration of Theorem 21.
Details are in the caption following the image
Figure 1 (b)
Open in figure viewerPowerPoint
Visual illustration of Theorem 21.
Details are in the caption following the image
Figure 1 (c)
Open in figure viewerPowerPoint
Visual illustration of Theorem 21.

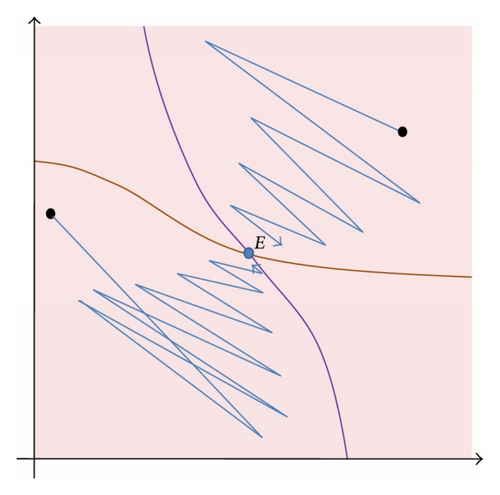
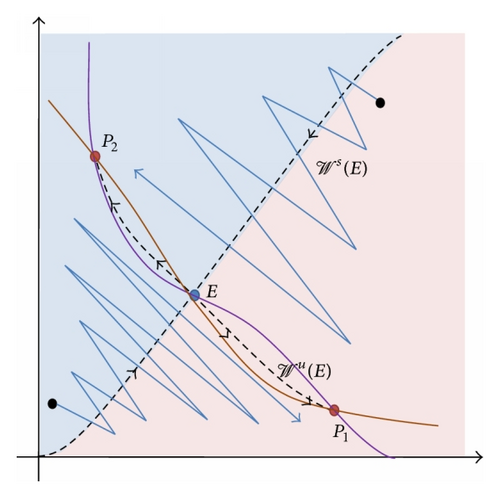
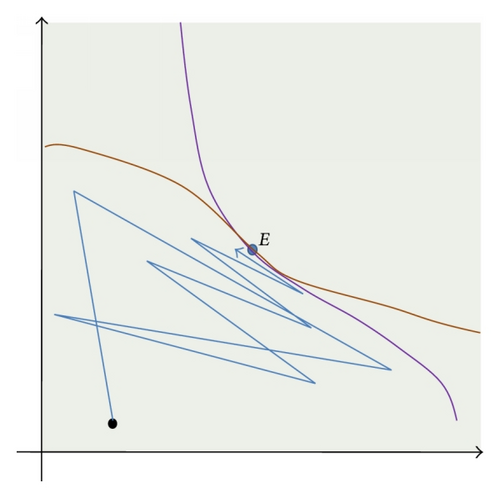
Based on our simulations, we pose the following conjecture.

Conjecture 22. The equilibrium of (90) is globally asymptotically stable for γ < C.

Clearly, if γ = C, then xn = 1, n = 1,2, … and so every solution is equal to the equilibrium solution. If γ < C, then the function f(u, v) = (u2 + γv)/(u2 + Cv) is increasing in u and decreasing in v. In addition, the interval ℐγ,C is an invariant interval for f. In order to apply Theorem 1.4.5 of [1], we need to show that the only solution of the system
()
in ℐγ,C is m = M. This system reduces to CMm = M3 − M2 + γM = m3 − m2 + γm. The polynomial G(u) = u3 − u2 + γu with G(0) = 0 is increasing on ℐγ,C, if G′(u) = 3u2 − 2u + γ ≥ 0, which holds when γ ≥ 1/3. Thus Conjecture 22 is true for γ ≥ 1/3.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgment

The authors are grateful to the anonymous referee for number of suggestions that have improved the quality of exposition of the results.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.