Discrete Dynamics in Nature and Society
Volume 2014, Issue 1 856475
Research Article
Open Access

Canard Limit Cycle of the Holling-Tanner Model

Chongwu Zheng, 

Chongwu Zheng

Department of Mathematics, Yuncheng University, Yuncheng, Shanxi 044000, China ycu.edu.cn

Search for more papers by this author
Fengqin Zhang, 

Corresponding Author

Fengqin Zhang

Department of Mathematics, Yuncheng University, Yuncheng, Shanxi 044000, China ycu.edu.cn

Search for more papers by this author
Jianquan Li, 

Jianquan Li

Science College, Air Force Engineering University, Xi’an 710051, China

Search for more papers by this author
First published: 16 July 2014
https://doi.org/10.1155/2014/856475
Academic Editor: Delfim F. M. Torres

Abstract

By using the singular perturbation theory on canard cycles, we investigate the canard phenomenon for the Holling-Tanner model with the intrinsic growth rate of the predator small enough. The obtained result shows that there may be at most one canard limit cycle, and the range of small parameters is estimated. The phenomenon of outbreak is explained.

1. Introduction

The predator-prey system
()
is referred to as the Holling-Tanner model [1]. In (1), the variables x(t) and y(t) denote the numbers of preys and predators at time t, respectively. r1 is the intrinsic growth rate of the prey, K is the carrying capacity of the prey, and function c1x/(x + a1), known as the functional response of Holling type II, is the rate at which predators consume the prey, where c1 is the maximum number of a predator and a1 is the half saturation value corresponding to the number of preys necessary to achieve one half of the maximum value. It is assumed that the predator grows logistically with intrinsic growth rate s1 and carrying capacity γx taking on the role of a prey-dependent carrying capacity for the predator, where γ is a measure of the quality of the prey as food for the predator. From the biological meaning all the parameters of (1) are positive.

It is easy to see that the set {(x, y):  0 < x ≤ K, y > 0} is positively invariant for (1), and there is always a unique positive equilibrium. The local stability of the positive equilibrium was analyzed in [2, 3]. In [4] Hsu and Huang considered the question of global stability of the equilibrium and obtained conditions under which its local stability implies the global stability. In 2003 Braza [5] investigated the existence of at least one limit cycle of (1) in a Hopf bifurcation. Gasull et al. [6] showed that (1) can exhibit two limit cycles by constructing an example. The bifurcation diagram of limit cycles of (1) was described to show the regions of parameters where two limit cycles or a semistable limit cycle appears [7]. Applying Andronov-Hopf bifurcation Theorem Hsu and Hwang proved that the Hopf bifurcation is subcritical and thus (1) may have at least two limit cycles for some parameter ranges and explained the phenomenon of outbreaking in [8] obtained by numerical simulations [9].

In the references mentioned above, it was assumed that all the parameters are positive constants, but there is not much consideration for the system with small parameters. It is interesting and important to analyze the bifurcation of limit periodic set of the system in the case when s1 is very small; that is, the intrinsic growth rate of the predator remains at a very low level. For this case when plotting the trajectories of system (1) with the intrinsic growth rate small enough by numerical simulations, it would take much longer time when the trajectory passes by the vertical y-axis. This behaves like the usual relaxation oscillation phenomena observed in slow-fast systems. By using the singular perturbation theory [10] Li and Zhu [11] studied the canard limit cycles for predator-prey system with functional response of four Holling types and developed criteria for the existence and multiplicity of canard slow-fast cycle (i.e., limit periodic set) in general predator-prey systems.

Although some references have considered the existence of two limit cycles for (1) [6, 7, 9], it is still interesting to discuss the existence of canard slow-fast cycle, since the canard slow-fast cycle consists of a part of the fast orbit and a part of the slow manifold and is the limit of a family of periodic orbits as the value of a positive parameter tends to zero. In this paper we mainly consider the existence of canard slow-fast cycle of (1) when s1 is very small. Our result shows that there may be at most one canard limit cycle, and the range of small parameters is estimated. In next section we first reduce the number of parameters to three ones by some transformation for (1) and introduce some concepts of canard slow-fast cycle. In Section 3 we provide the complete inferences for the main result of this paper. Finally we give discussion according to the results of numerical simulation.

2. Simplification of the Model and Canard Limit Cycle

For the case where s1 is very small, let
()
where ε1 is positive and λ1 may be negative, and we will choose ε1 and |λ1| small enough to make a2 > 0 in later discussion; then system (1) becomes
()
For system (3), making the scaling
()
and then dropping their bars yield
()
where
()
Since x > 0 and a > ελ, letting dt = ((x + a − ελ)/x)dτ gives the equivalent system of (5):
()
where
()
If we introduce slow time t = ετ, then system (7) is transformed to
()
By lettng ε = 0 for (7) and (9), we obtain the layer equations
()
and the reduced equations
()
respectively.
In this paper we will always assume that a < 1. The slow manifold S = {(x, y):  y = f0(x)} has a unique extreme point at
()
and it is a simple maximum point; see Figure 1(a). Besides, S is globally concave for x ≥ 0. The fast movement of the layer equations (10) is shown in Figure 1(b), where the orbits outside S are parallel lines {y = c} with different constant c, and the curve S consists of singular points; hence it is also called the critical curve. Note that the points on S left to (x0, y0) are normally hyperbolic repelling while the points on S right to (x0, y0) are normally hyperbolic attracting.
Details are in the caption following the image
Figure 1 (a)
Open in figure viewerPowerPoint
The limit periodic cycle Γ(s) and the slow manifold S.
Details are in the caption following the image
Figure 1 (b)
Open in figure viewerPowerPoint
The limit periodic cycle Γ(s) and the slow manifold S.
To study the slow movement on S∖{(x0, y0)}, from the reduced equations (11) we have
()
and hence along S the slow movement is controlled by
()

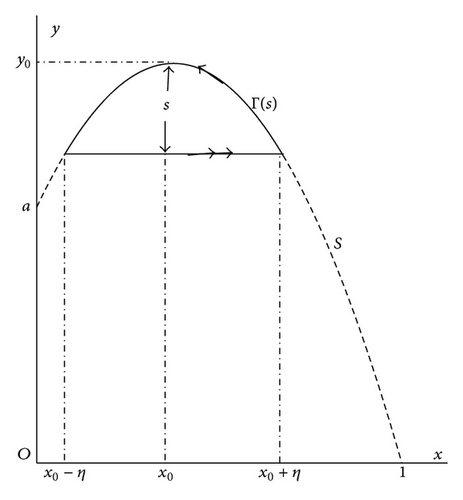
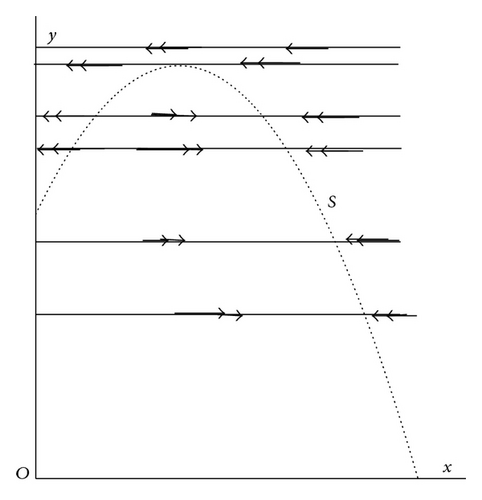
In order to show the existence of canard slow-fast cycle, from Figure 1(b) it is necessary to illustrate that the right hand side of (14) should be negative near the point (x0, y0).

In the next section, we will make some transformations such that the function g(x, y) in system (7) becomes , and for λ = 0 the right hand side of (14) is negative in an interval of x, containing x0; then we may construct a slow-fast cycle (i.e., limit periodic set) Γ(s) by combining a part of the fast orbit y = y0 − s, where s ∈ (0, y0 − a), and a part of the slow manifold S, shown in Figure 1(a). As we mentioned above, on the left and right sides of the point (x0, y0) the points on the slow manifold S are normally hyperbolic repelling and attracting, respectively, the point (x0, y0) is called a canard point, and the slow-fast cycle Γ(s) is called a canard type, or simply called a canard slow-fast cycle; see [10, 12].

3. Existence and Uniqueness of Canard Slow-Fast Cycles

To study the local behavior of system (7) near (x0, y0), we make the change of coordinates
()
For (u, v) near (0,0) system (7) becomes
()
where
()
Notice that as b0 = 0 (i.e., δx0 = y0); then b > 0 for some δ and a making |b0| small enough. For such δ and a, making one more change of coordinates
()
equation (16) becomes
()
In addition, we choose δ and a such that
()
and then (19) can be rewritten as
()
where
()
From (17) and (20) we have
()
()
Furthermore, implies that the change of coordinates (18) is available.
According to (3.12) and (3.13) of [10], from (24) we have
()
and then
()
Therefore, the canard cycle of (7) is asymptotically stable if it exists.
On the other hand, for (14) we have
()
for a < 1 and x < 1. The fact that for x > 0 and x ≠ x0 implies that system (14) along the slow manifold S is well defined near x0 and that the point (x0, y0) is a canard one.
Further, by Theorems 3.3 of [10], A < 0 implies that a ε-family of canard cycles bifurcates from the limit periodic set Γ(s), for each s ∈ (0, y0 − a), and for some small and 0 < ε ≪ 1. Moreover, satisfies
()
where σ ∈ (0,1) is a constant and
()

The inequality (28) implies that, when there is a family of canard cycles bifurcating from the canard slow-fast cycle, λ in (7) depends on ε, and λ → 0 as ε → 0.

Further, direct computation shows
()
According to the symmetry of the slow manifold S about x = (1 − a)/2, for λ = 0 (i.e., δ = δ0) we suppose that the interval of x-coordinate of the slow-fast cycle Γ(s) is [(1 − a)/2 − η, (1 − a)/2 + η], where η ∈ (0, (1 − a)/2) and s ∈ (0, y0 − a); see Figure 1(a). By straightforwardly calculating, we have
()
where
()
Note that
()
for 0 < a < 1 and 0 < η < (1 − a)/2; then h(0) = 0 implies that h(η) > 0 for 0 < η < (1 − a)/2; that is, I(s, δ0) < 0 for 0 < s < y0 − a. Hence, it follows form the results in [12] that (7) has at most one canard slow-fast cycle.

Summarizing the above inference, we obtain the following result.

Theorem 1. When a < 1, (7) has at most one canard slow-fast cycle, which is asymptotically stable for 0 < ε ≪ 1 and λ satisfying (28).

4. Numerical Simulation and Discussion

We first plot the trajectories of (5) and the corresponding curves of x = x(t) and y = y(t) as δ = 3.2, a = 0.15, ϵ = 0.005, and λ = 0.001 (see Figure 2), in which Figures 2(b) and 2(c) illustrate the existence of the fast stages of x = x(t) and y = y(t).

Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
The trajectories of (5) with the fast stage and the slow stage and the corresponding curves of x = x(t) and y = y(t), where δ = 3.2, a = 0.15, ϵ = 0.005, and λ = 0.001.
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
The trajectories of (5) with the fast stage and the slow stage and the corresponding curves of x = x(t) and y = y(t), where δ = 3.2, a = 0.15, ϵ = 0.005, and λ = 0.001.
Details are in the caption following the image
Figure 2 (c)
Open in figure viewerPowerPoint
The trajectories of (5) with the fast stage and the slow stage and the corresponding curves of x = x(t) and y = y(t), where δ = 3.2, a = 0.15, ϵ = 0.005, and λ = 0.001.
Note that the vertical and horizontal isoclines of (5) divide the first quadrant of the (x, y)-plane into four regions:
()
And from (2) and (6) it follows that r1 = c1γ/δ, a1 = (a − ελ)K, and s1 = c1γε, where α, δ, ε, and λ are the parameters in (5); then, corresponding to (1), the value of parameter s1 is very small relative to other parameters as ε is very small.

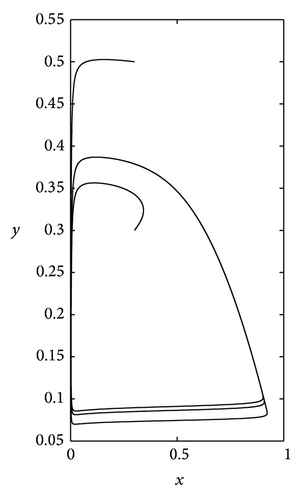
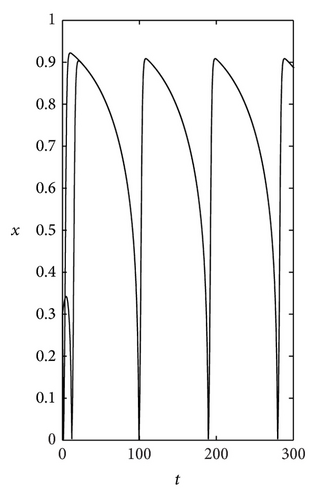
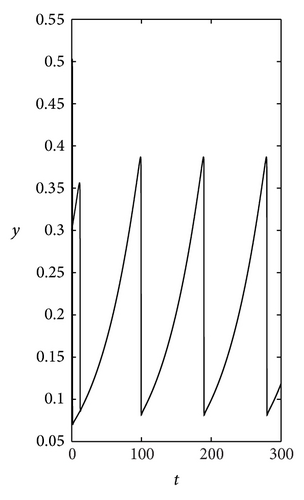
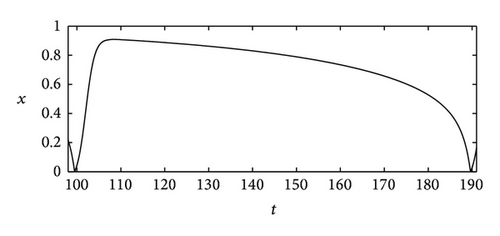
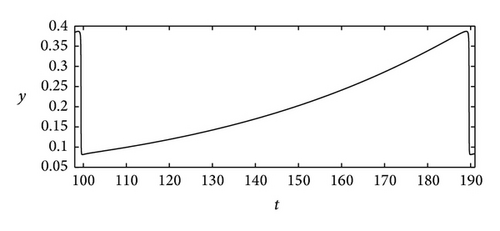
In order to more clearly show the fast stages, we locally enlarge the two curves in Figures 2(b) and 2(c) into Figures 3(a) and 3(b), respectively. From Figures 3(a) and 3(b), we can know that the fast stages of x = x(t) occur in region D1, and those of y = y(t) occur in region D3. Biologically, x = x(t) and y = y(t) represent the numbers of preys and predators at time t, respectively; then, when the intrinsic growth rate of the predator is very small and there exists the periodic solution for (1), according to signs of derivatives of x(t) and y(t) with respect to time t, the number of the preys increases quickly from the number small enough as (x(t), y(t)) ∈ D1, and the number of the predators decreases quickly as (x(t), y(t)) ∈ D3. The quick increase of the prey from the small value may explain the phenomenon of outbreak in [8].

Details are in the caption following the image
Figure 3 (a)
Open in figure viewerPowerPoint
The curves of x = x(t) and y = y(t) obtained by locally enlarging the curves of x = x(t) and y = y(t) in Figure 2, respectively.
Details are in the caption following the image
Figure 3 (b)
Open in figure viewerPowerPoint
The curves of x = x(t) and y = y(t) obtained by locally enlarging the curves of x = x(t) and y = y(t) in Figure 2, respectively.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgment

This work is supported by the National Natural Science Fund of China (nos. 11371369 and 11371313).

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.