Stability of a Class of Fractional-Order Nonlinear Systems
Abstract
In this letter stability analysis of fractional order nonlinear systems is studied. Some new sufficient conditions on the local (globally) asymptotic stability for a class of fractional order nonlinear systems with order 0 < α < 2 are proposed by using properties of Mittag-Leffler function and the Gronwall inequality. And the corresponding stabilization criteria are also given. The numerical simulations of two systems with order 0 < α < 1 and two systems with order 1 < α < 2 illustrate the effectiveness and universality of the proposed approach.
1. Introduction
During the last decade the fractional calculus has gained importance in both theoretical and applied aspects of several branches of science and engineering. There are two essential differences between integer order derivation and fractional order derivation. Firstly, the integer order derivative indicates a variation or certain attribute at particular time for a mechanical or physical process, while the fractional order derivative is concerned with the whole time domain. Secondly, the integer order derivative describes the local properties of a certain position, while the fractional order derivative is related to the whole space for a physical process. Then many physical systems are well characterized by the fractional order state equations [1–4], such as fractional order Lotka-Volterra equation [1] in biological systems, fractional order Schödinger equation [2] in quantum mechanics, fractional order Langevin equation [3] in anomalous diffusion, and fractional order oscillator equation [4] in damping vibration.
However there are several open problems in this area. Stability of fractional order systems is one of the most fundamental and important issues. On the other hand, because fractional differential operators are nonlocal and have weakly singular kernels, some methods in dealing with interorder systems cannot be simply extended to fractional-order methods. To the best of knowledge, the stability of fractional-order nonlinear systems is still relatively few. Reference [5–7] investigated the necessary and sufficient stability conditions for linear fractional order differential equations and linear time-delayed fractional differential equations. The stability of n-dimensional linear fractional order differential systems with order 1 < α < 2 has already been studied in [8]. However, only under some special circumstances or in certain cases, the practical problems may be regarded as linear systems. Therefore, stability of nonlinear system is of great significance, and it also has important value in application. In [9], the stability of fractional nonlinear time-delay systems for Caputo’s derivative are investigated, and two theorems for Mittag-Leffler stability of the fractional order nonlinear time-delay systems are proved. In [10], the authors proposed the finite-time stabilization of a class of multistate time delay of fractional nonlinear systems. In [11, 12], the authors studied the stability of fractional nonlinear dynamic systems using Lyapunov direct method with the introductions of Mittag-Leffler stability and generalized Mittag-Leffler stability notions. In [13], the authors studied fractional order Lyapunov stability theorem and its applications in synchronization of complex dynamical networks. In [14], some new sufficient conditions ensuring asymptotical stability of fractional-order nonlinear system with delay are proposed firstly.
In this paper the stability of nonlinear fractional order nonlinear system is studied. And by using the Gronwall inequality and the properties of Mittag-Leffler function, we proposed some new sufficient conditions on the local (globally) asymptotic stability for a class of fractional order nonlinear systems with order 0 < α < 2. And the corresponding stabilization criteria are also given. Finally, four numerical simulation examples have illustrated the effectiveness and universality of the proposed methods.
2. Fractional Order Derivative and Mittag-Leffler Function
2.1. Definitions of Fractional Derivative and Mittag-Leffler Function
Fractional calculus plays an important role in modern science [15–17]. Some definitions for fractional derivatives are usually used, such as Grünwald-Letnikov (GL), Riemann-Liouville (RL), and Caputo definition. In this paper, we mainly use the Caputo definitions [15].
Definition 1 (see [15].)The fractional integral of function f(t) is defined as follows:
Definition 2 (see [15].)The Caputo derivative with order α of function f(t) is given as
The formulas for Laplace transform of the Caputo fractional derivative have the following form [16]:
As a generalization of the exponential function which is frequently used in the solutions of integer-order systems, the Mittag-Leffler function is frequently used in the solutions of fractional systems. The definition and properties are given in the following.
Definition 3 (see [17].)The Mittag-Leffler function is given as
Remark 4. If β = 1, we have Eα,1(z) = Eα(z), especially, E1,1(z) = E1(z) = ez.
2.2. Properties of Mittag-Leffler Functions and the Gronwall Inequality
In this section, we give the Gronwall inequality and some important properties of the Mittag-Leffler functions which are used in the following.
Lemma 5 (see [15].)Considering the Laplace transform of Mittag-Leffler function with two parameters, we have
Proof. The proof of this Lemma can be found in [15].
Lemma 6 (see [18], [19].)If 0 < α < 2, , and μ satisfies πα/2 < μ < min{π, πα}, there exist C1 > 0 and C2 > 0 such that
Lemma 7 (see [18], [19].)For the Mittage-Leffler function Eα,β(Atα), there exist finite real constants , , and such that
Proof. The proof of this Lemma can be found in [18].
Lemma 8 (Gronwall inequality [19, 20]). Let α > 0, u(t) is a nonnegative function locally integrable on [0, T) and a(t) is a nonnegative, nondecreasing continuous function defined on [0, T), a(t) < M (constant), and suppose z(t) is nonnegative and locally integrable on [0, T) with
3. Stability and Stabilization of Fractional Order Nonlinear System
3.1. Stability and Stabilization of Fractional Order Nonlinear System with Order 0 < α < 1
Theorem 9. The fractional order nonlinear system (12) is local asymptotically stable, if it satisfies the following conditions: (1)Re( eig (A)) < 0 and ω = − max Re( eig (A)) > Γ(α), where Γ(·) is the gamma function; (2) g(x(t)) satisfies ‖g(x(t))‖ = o‖x(t)‖ as ‖x‖ → 0.
Proof. Applying the Laplace transform on (12), we have
Theorem 10. The fractional order nonlinear system (12) is globally asymptotically stable, if it satisfies the following conditions: (1) g(x(t)) satisfies g(0) = 0 and the Lipschitz condition with respect to x, that is, ‖g(x1) − g(x2)‖ ≤ L‖x1 − x2‖; (2)Re( eig (A)) < 0 and ω = − max Re( eig (A)) > LM3M4Γ(α), where M3 and M4 satisfy ∥eAt∥≤M3e−ωt and .
Proof. Applying the Laplace transform and Laplace inverse transform on (12), we obtain the solution of (12),
Therefore, our aim is to design a suitable feedback gain matrix K such that the controlled system is local (globally) asymptotically stable.
Theorem 11. The controlled fractional order nonlinear system (28) is local asymptotically stable, if it satisfies the following conditions: (1) and ; (2) g(x(t)) satisfies ‖g(x(t))‖ = o‖x(t)‖ as ‖x‖ → 0.
Proof. The proof is similar to that of Theorem 9.
Theorem 12. The controlled fractional order nonlinear system (28) is globally asymptotically stable, if it satisfies the following conditions: (1) g(x(t)) satisfies g(0) = 0 and the Lipschitz condition with respect to x, that is, ‖g(x1) − g(x2)‖ ≤ L‖x1 − x2‖; (2) and , where M3 and M4 satisfy and .
Proof. The proof is similar to that of Theorem 10.
3.2. Stability and Stabilization of Fractional Order Nonlinear System with Order 1 < α < 2
Theorem 13. The fractional order nonlinear system (29) is local asymptotically stable, if it satisfies the following conditions: (1)Re(eig(A)) < 0 and ω = −max Re(eig(A)) > Γ(α) 1/α; (2) g(x(t)) satisfies ‖g(x(t))‖ = o‖x(t)‖ as ∥x∥→0.
Proof. Applying the Laplace transform on (29), we have
Theorem 14. The fractional order nonlinear system (29) is globally asymptotically stable, if it satisfies the following conditions: (1) g(x(t)) satisfies g(0) = 0 and the Lipschitz condition with respect to x, that is, ‖g(x1) − g(x2)‖ ≤ L‖x1 − x2‖; (2)Re(eig(A)) < 0 and ω = −max Re(eig(A)) > LM3M4Γ(α), where M3 and M4 satisfy ‖eAt‖ ≤ M3e−ωt and .
Proof. Applying the Laplace transform and Laplace inverse transform on (29), we obtain the solution of (29),
Therefore, our aim is to design a suitable feedback gain matrix K such that the controlled system is local (globally) asymptotically stable.
Theorem 15. The controlled fractional order nonlinear system (45) is local asymptotically stable, if it satisfies the following conditions: (1) and ; (2) g(x(t)) satisfies ‖g(x(t))‖ = o‖x(t)‖ as ‖x‖ → 0.
Proof. The proof is similar to that of Theorem 13.
Theorem 16. The controlled fractional-order nonlinear system (45) is globally asymptotically stable, if it satisfies the following conditions: (1) g(x(t)) satisfies g(0) = 0 and the Lipschitz condition with respect to x, that is, ‖g(x1) − g(x2)‖ ≤ L‖x1 − x2‖; (2) and , where M3 and M4 satisfy and .
Proof. The proof is similar to that of Theorem 14.
Remark 17. There are many fractional order chaotic (hyperchaotic) systems which satisfy ‖g(x(t))‖ = o‖x(t)‖ as ‖x‖ → 0 or the Lipschitz condition, such as fractional order Lorenz system, fractional order Chen system, fractional order Lü system, fractional order Liu system, and so forth [22]. Therefore, Theorems 9–16 can be used as the criteria to control chaos in a class of fractional-order systems. Compared with nonlinear control methods, the advantage of linear control lies in reducing control cost and is easy to implement.
Remark 18. The obtained sufficient conditions could be applied to a class of fractional order hyperchaotic systems [23–25]. On the one hand, complex multiscroll chaotic systems have garnered much attention in recent years. J. H. Lü has done a large amount of remarkable work. In fact, the sufficient conditions could be applied to a class of complex multiscroll chaotic systems, which could also generate a complex four-scroll chaotic attractor.
4. Four Illustrative Examples
In this section, we apply the proposed method in stabilizing a fractional order Chen system, Chua system, Lü system, and Liu system to verify its effectiveness and universality.
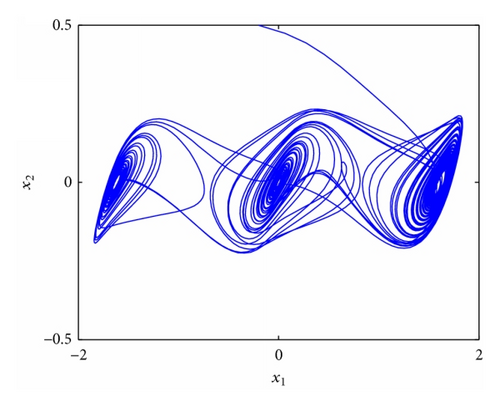
4.1. Stabilization of Fractional Order Chaotic Chen System

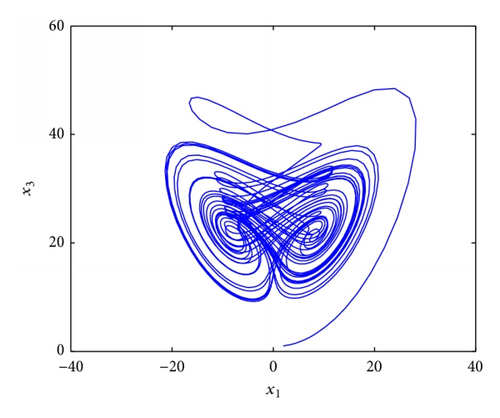
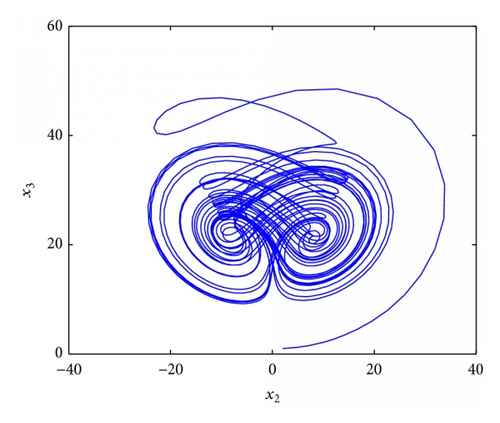
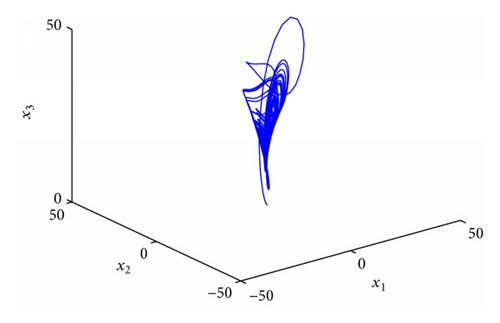
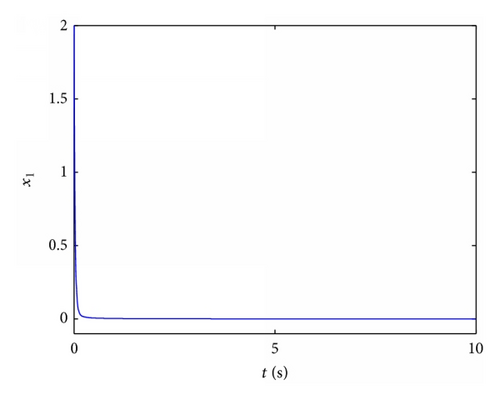
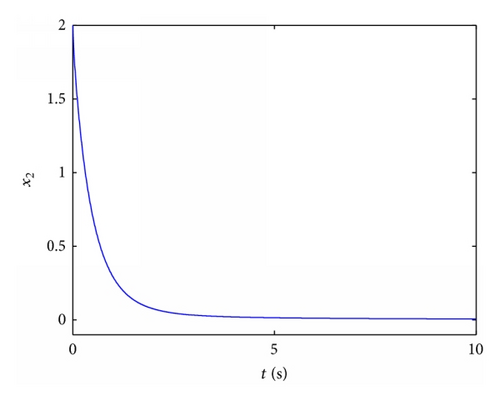
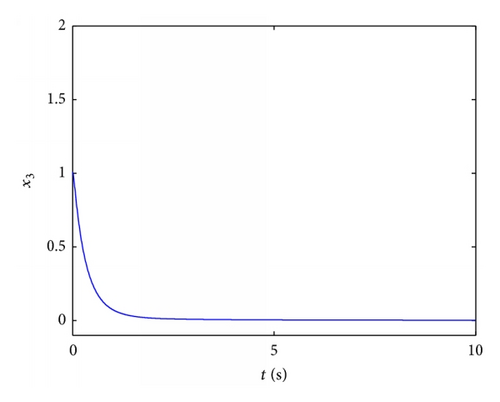
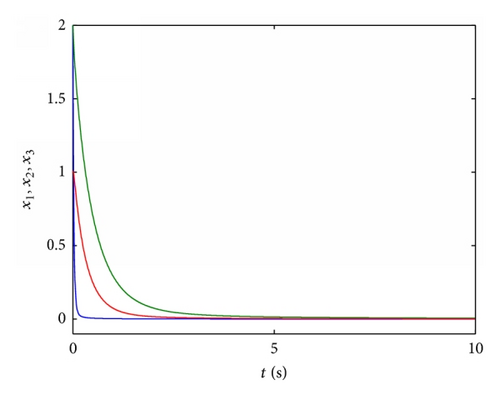
4.2. Stabilization of Fractional Order Chaotic Chua System
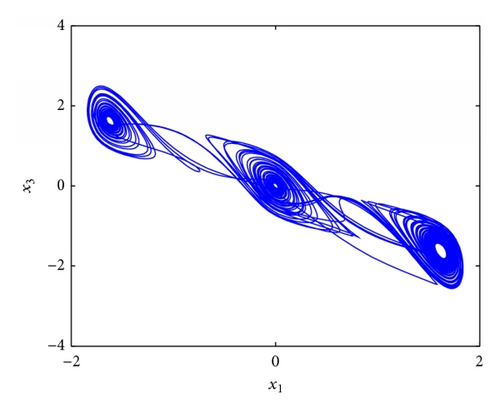
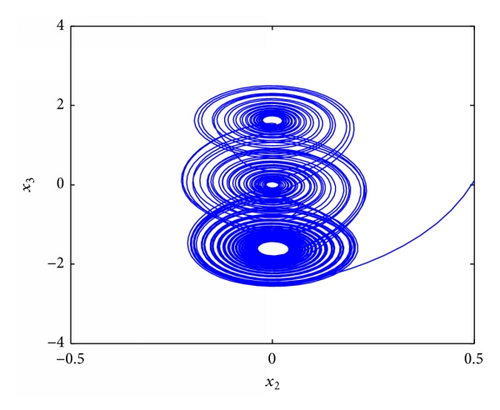
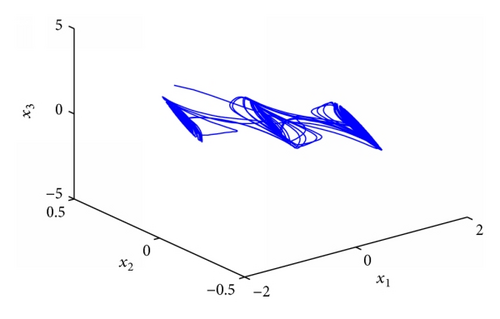
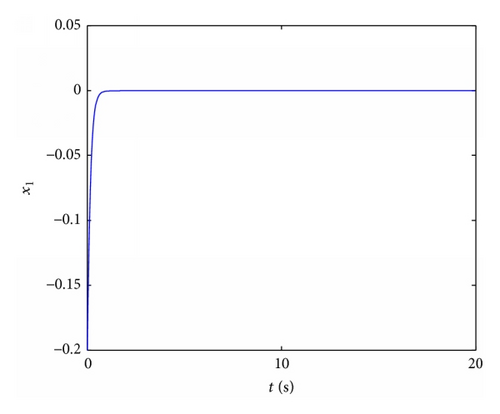
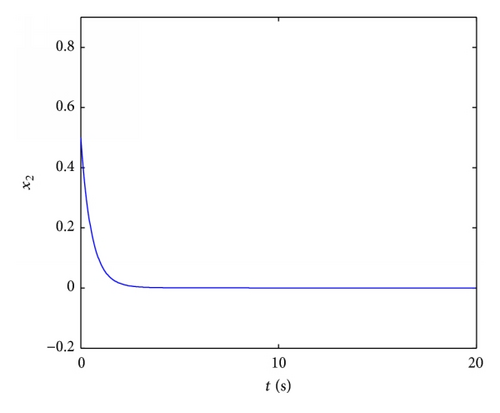
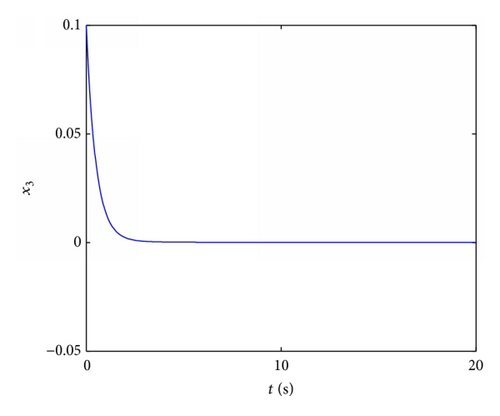
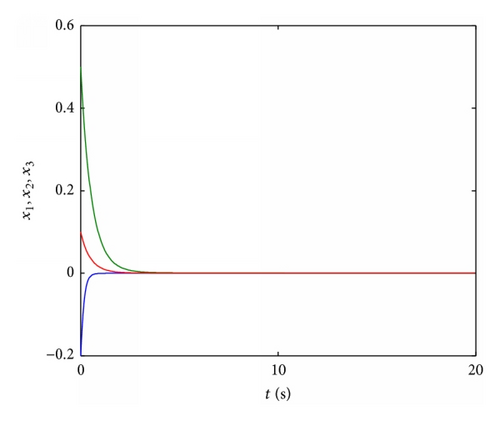
4.3. Stabilization of Fractional Order Chaotic Lü System
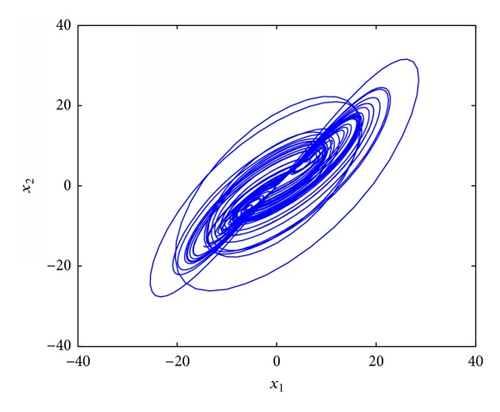
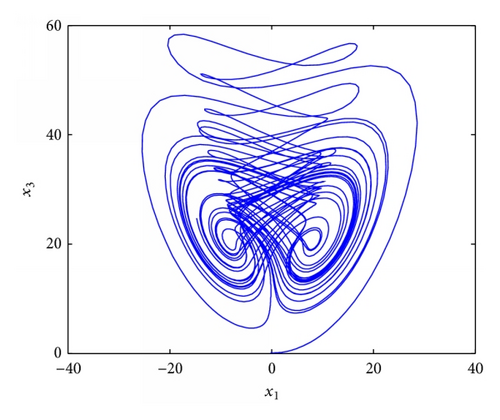
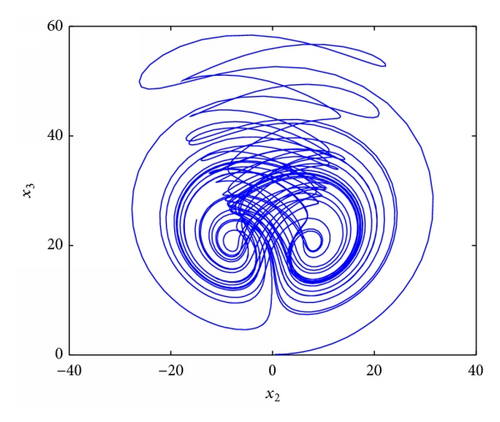
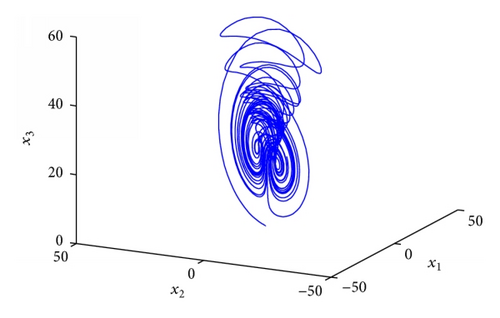

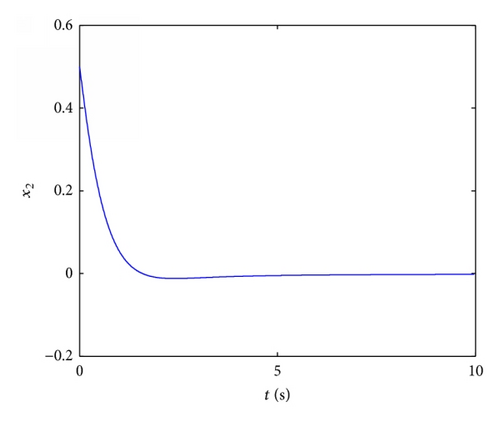
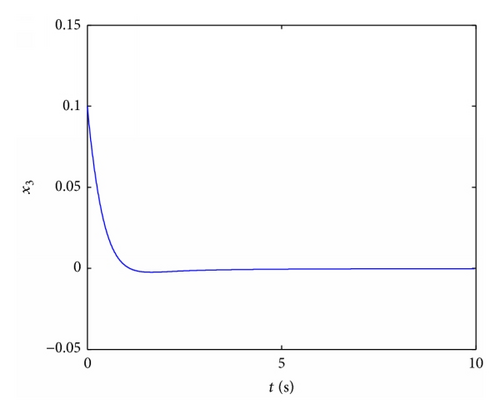
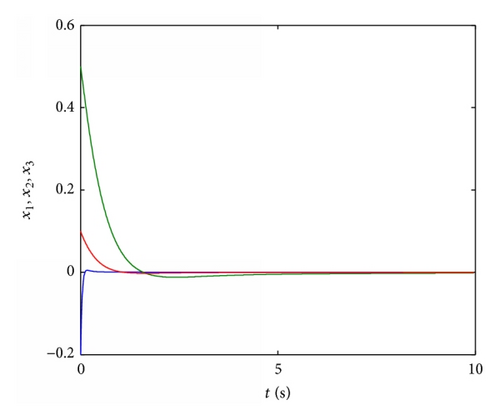
4.4. Stabilization of Fractional Order Chaotic Liu System
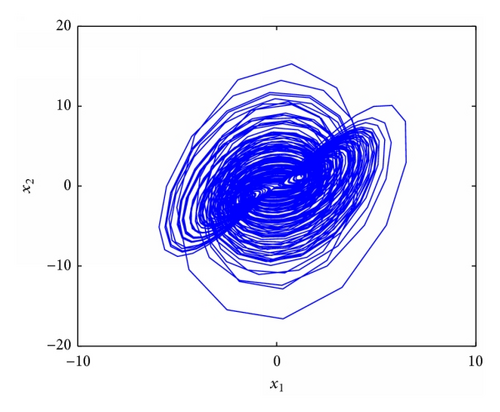
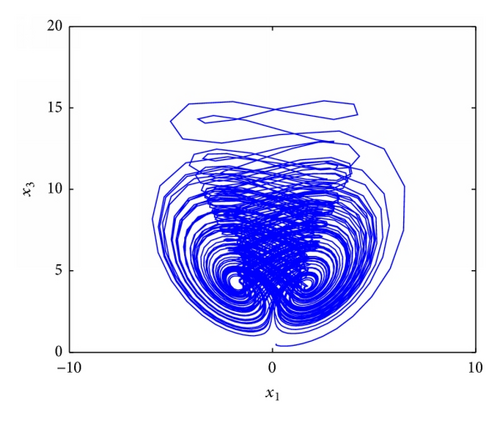
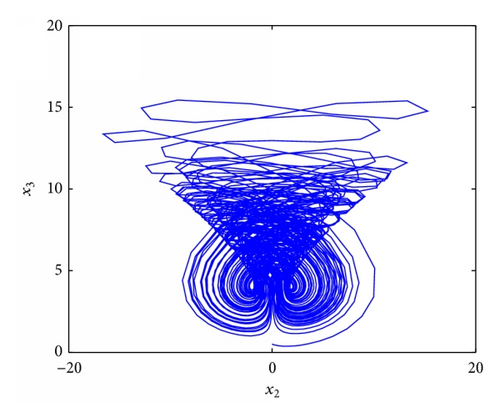


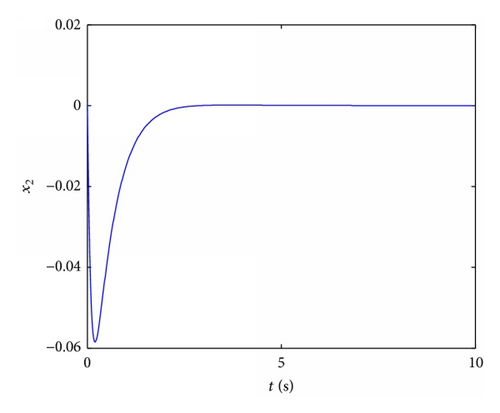
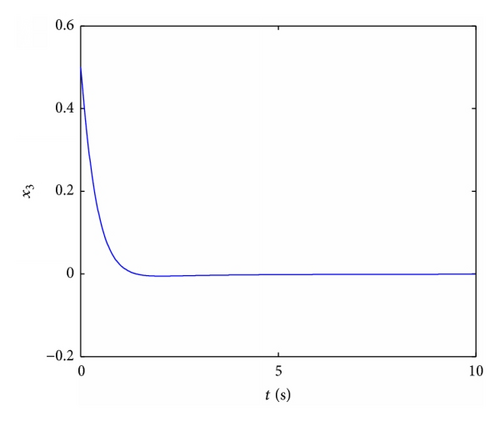
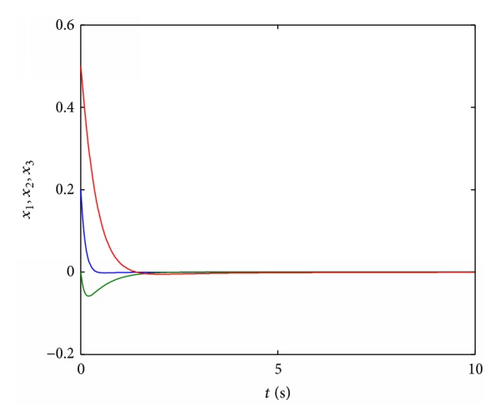
5. Conclusion
Stability of the nonlinear dynamical systems is important for scientists and engineers. Fractional dynamic systems were used intensively during the last decade in order to describe the behavior of complex systems in physical and engineering. In this paper the stabilization of nonlinear fractional order dynamic system is studied. And by using the Gronwall inequality and the properties of Mittag-Leffler function, we proposed some new sufficient conditions on the local (globally) asymptotic stability for a class of fractional order nonlinear systems. Finally the corresponding stabilization criteria are also given. Four numerical simulation examples have illustrated the effectiveness and universality of the proposed methods.
Conflict of Interests
The authors declare that there is no conflict of interests regarding the publication of this paper.
Acknowledgments
This work is supported by the Artificial Intelligence Key Laboratory of Sichuan Province 2014RYJ05 and Sichuan University of Science and Engineering Grants 2012PY17, 2014PY06, 2014RC03, and 2013KY02.




