Volume 2014, Issue 1 712682

Research Article

Open Access

Multiple Model Identification for a High Purity Distillation Column Process Based on EM Algorithm

Corresponding Author

Weili Xiong

[email protected]

Key Laboratory of Advanced Process Control for Light Industry (Ministry of Education), School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China jiangnan.edu.cn

Search for more papers by this author

Lei Chen,

Lei Chen

Key Laboratory of Advanced Process Control for Light Industry (Ministry of Education), School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China jiangnan.edu.cn

Search for more papers by this author

Fei Liu,

Fei Liu

Key Laboratory of Advanced Process Control for Light Industry (Ministry of Education), School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China jiangnan.edu.cn

Search for more papers by this author

Baoguo Xu,

Baoguo Xu

Key Laboratory of Advanced Process Control for Light Industry (Ministry of Education), School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China jiangnan.edu.cn

Search for more papers by this author

Weili Xiong,

Corresponding Author

Weili Xiong

[email protected]

Key Laboratory of Advanced Process Control for Light Industry (Ministry of Education), School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China jiangnan.edu.cn

Search for more papers by this author

Lei Chen,

Lei Chen

Key Laboratory of Advanced Process Control for Light Industry (Ministry of Education), School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China jiangnan.edu.cn

Search for more papers by this author

Fei Liu,

Fei Liu

Key Laboratory of Advanced Process Control for Light Industry (Ministry of Education), School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China jiangnan.edu.cn

Search for more papers by this author

Baoguo Xu,

Baoguo Xu

Key Laboratory of Advanced Process Control for Light Industry (Ministry of Education), School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China jiangnan.edu.cn

Search for more papers by this author

First published: 13 February 2014

https://doi.org/10.1155/2014/712682

Citations: 4

Academic Editor: Shuping He

Share a link

Email
Wechat
Bluesky

Abstract

Due to the strong nonlinearity and transition dynamics between different operating points of the high purity distillation column process, it is difficult to use a single model for modeling such a process. Therefore, the multiple model based approach is introduced for modeling the high purity distillation column plant under the framework of the expectation maximization (EM) algorithm. In this paper, autoregressive exogenous (ARX) models are adopted to construct the local models of this chemical process at different operating points, and the EM algorithm is used for identification of local models as well as the probability that each local model takes effect. The global model is obtained by aggregating the local models using an exponential weighting function. Finally, the simulation performed on the high purity distillation column demonstrates the effectiveness of the proposed method.

1. Introduction

The increasing complexity of the process control systems poses a great challenge for process modeling and parameter identification and control. In practice, most of the industrial processes show a strong nonlinearity and a dynamic nature. Therefore, it is of interest for both academic researchers and industrial practitioners to study how to model these systems and to achieve satisfactory or even optimal control performance. Linear modeling technologies have been quite sophisticated after decades of development; however, due to the inborn nonlinearity of some production processes, the performance of single linear model based controllers or optimizers may be compromised or even unsatisfactory [1]. To overcome the limitations imposed by the nonlinearity of the process, various strategies have been developed for nonlinear process modeling. Some of the popular modeling approaches have been proposed and applied in industrial processes, such as artificial neural networks [2, 3], support vector regression and its extension least squares support vector regression [4], Gaussian process regression [5], and hybrid methods [6]. The obvious feature of these methods is that they do not need any prior knowledge about the system. However, these methods do not always capture the process dynamics well and may lose validity when the system transits among a large range of operation.

The multiple model approach is a good compromise which produces complex models or controllers by piecing a number of simpler subsystems together. Some multiple modeling strategies and applications have been investigated because they are able to represent complex nonlinear processes using the linearization technique [7]. The terminology of linear parameter varying (LPV) modeling method, which is featured by its linear structure and varying model parameters, was introduced by Shamma and Athans [8, 9]. The work on identification of multimodel LPV models can be found in much literature. For example, Zhu and Xu proposed an LPV model based on blended linear models and added weights at the input side [10, 11]. The identification of LPV models in an input-output setting with Box-Jenkins (BJ) model structure was addressed by Zhao et al. and prediction error method was employed for parameter interpolation [12]. Huang et al. studied the work of the multiple LPV model identification using several weighting functions with two scheduling variables [13]. The multiple model based recursive least square parameter identification was illustrated by Chen and Liu [14]. Jin et al. proposed a multiple model LPV approach for nonlinear systems under the framework of the expectation maximization (EM) algorithm [15]. It is an important step on LPV identification in which the model identity is treated as the missing variable in the EM scheme. Based on the EM algorithm, the local models are synthesized with process data to obtain a global model for approximating a nonlinear process. Deng and Huang extended the identification method to nonlinear parameter varying systems in which the local model takes the form of state space equation. The identification problem is solved by using the particle filter based on EM algorithm [16]. The efficiency is illustrated on numerical examples and a pilot-scale hybrid water tank. Chen et al. continued to study the uncertain scheduling variable problem in multiple model based nonlinear identification. Both the linear and the nonlinear dynamics of scheduling variables are taken into account [17].

The distillation column is considered as one of the most important unit operations in chemical engineering [18, 19]. It becomes a benchmark problem in chemical process control for nonlinear modeling technology. The difficulties in modeling and controlling distillation columns lie in their highly nonlinear characteristics. Modeling of distillation columns may be classified into three groups: fundamental modeling, empirical modeling, and hybrid modeling [18]. In this paper, a hybrid solution based on the multiple models is adopted, which combines the two main advantages of linear and nonlinear models. The distillation column model is a nonlinear global model but can be represented as a reunion of linear models, one linear model for each operating point (local model or submodel), where each local model works at different operating point and can be identified through the iteration procedure of the EM algorithm. Finally, the global nonlinear model can be obtained by using the exponential function which takes full account of each operating point.

The remainder of this paper is organized as follows: the high purity distillation column used to test the multiple model method is described in Section 2. Section 3 lays out the mathematical formulation of the multiple model approach in which the ARX model is used as the local model. In Section 4, the identification procedure under the EM algorithm is provided. The simulation on the high purity distillation column with multiple inputs is given in Section 5. Finally, conclusions are given in Section 6.

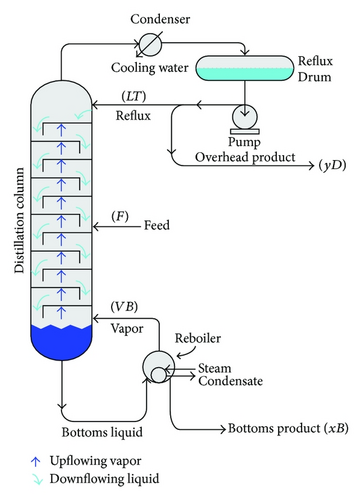
2. Description of a High Purity Distillation Column

Distillation is simply defined as a process in which a liquid or vapor mixture of two or more substances is separated into its component fractions of desired purity, by the application and removal of heat [20]. The process is based on the fact that the vapor of a boiling mixture will be richer in the components that have lower boiling points. In most cases, the distillation is operated at a continuous steady state. New feed is always being added to the distillation column and products are always being removed. A high purity distillation column is strongly nonlinear, and any realistic study should take this into account [21, 22]. Distillation column has become a favorite subject in the process control engineering field, including the areas of soft-sensor, process modeling, and control. There are a variety of configurations for distillation columns, and each performs specific types of separations [23].

A typical two-product distillation column on a pilot plant scale is shown in Figure 1. Some important notation is summarized in Table 1. It is a nonlinear model of a distillation column with NT − 1 theoretical stages including a reboiler plus a total condenser [24]. In the model, the following assumptions are made:

(1)
two components (binary separation);
(2)
one feed and two products;
(3)
constant relative volatility;
(4)
constant molar flows (same vapor flow on all stages);
(5)
no vapor holdup;
(6)
total condenser.

Table 1. Notation of the distillation column in reflux and boil-up construction.

	Variable	Description	Unit
1	F	Feed rate	kmol/min
2	yD	Distillate top product composition	mole fraction
3	xB	Distillate bottom product composition	mole fraction
4	LT	Reflux flow	kmol/min
5	VB	Boil-up flow	kmol/min

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The two-product distillation column in reflux and boil-up construction.

3. Problem Formulation Using Multiple Model Method

The high purity distillation column as mentioned above is a classic chemical production process; the plant may transit among several operating points. A bank of ARX models is employed to approximate the nonlinear dynamic process around each operating point. Consider the following ARX model [15, 17]:

(1)

where {y_k ∈ ℝ, k = 1,2, …, N} is the output. e_k is the Gaussian noise with zero mean and variance σ added to the ARX model. x_k ∈ ℝⁿ is the regressor vector,

(2)

where {u_k ∈ ℝ^m, k = 1,2, …, N} is the input of the nonlinear system, n_a and n_b are the orders of the output and input, and n = n_a + m · n_b. Many industrial processes are often operated in certain “orderly” ways to meet different production objectives. Such orderly ways are also referred to as operating trajectory consisting of several predesigned operating points which are defined as the scheduling variable, W = w_1:N = {w₁, w₂, …, w_N}. Here we assume that M different operating points are known a priori, corresponding to a certain {T_i, i = 1,2, …, M}, namely, T_1:M.

Around the small region of each of the operation points, the ARX local model can be used to approximate the process dynamics. Here parameter θ_i is used to represent the ith local model parameters. Let U = u_1:N denote the sequence of input data set {u₁, u₂, …, u_N} and let Y = y_1:N denote the observed output data set {y₁, y₂, …, y_N}. Here a hidden variable I = I_1:N = {I₁, I₂, …, I_N} is introduced to stand for the identity of each local model that takes effect at sampling time point k. So the parameters to be estimated for each local model are

. Given all of the past observed data information, the probability of the output y_k can be computed as

(3)

Based on the fact that the observed output y_k at kth sampling time instant directly depends on the regressor vector x_k as well as the data identity of I_k, (3) can be further written as

(4)

Here α_k,i is the normalized weight standing for the probability that the ith submodel takes effect at time k. An exponential function is adopted as

(5)

where w_k is the scheduling variable at the sampling time k and o_i is defined as the validity width of the ith local model which is limited between o_min⁡ (the lower bound for o_i, i = 1,2, …, M) and o_max⁡ (the upper bound for o_i, i = 1,2, …, M).

The missing data set is the random variable I = {I₁, I₂, …, I_N} denoting the identity of each local model, namely, C_mis = {I}. The values of input variables, output variables, and the scheduling variable are observed or given a priori, so C_obs = {U, Y, W, T_1:M}. The parameters to be estimated from process input and output data under the framework of the EM algorithm are Θ = {θ_i, o_i, σ} _i=1,2,…,M.

4. The ARX Model Identification under the EM Algorithm

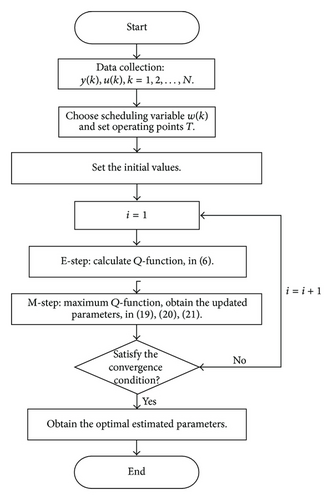
4.1. The EM Algorithm Review

The EM algorithm is an efficient iterative procedure for maximum likelihood estimation in the presence of missing data. The main strength of the EM algorithm lies in its ability to handle missing variables in the identification data set [25]. After being first introduced by Raghavan et al., it has found extensive applications in various areas for finding maximum likelihood estimates of parameters in probabilistic models [26]. In the EM procedure, both the complete data log likelihood p(C_obs, C_mis∣Θ) and the conditional predictive distribution of missing data p(C_mis∣C_obs, Θ^old) are needed to be calculated. There are two steps, namely, the expectation step (E-step) and the maximization step (M-step). The EM algorithm proceeds as follows.

(1)
Initialization: give an initial value of the model parameter vector.
(2)
E-step: the Q-function is calculated, given the current parameter Θ estimated from the previous iteration,
(6)
(3)
M-step: maximize the Q-function with respect to Θ to obtain the new iterative parameter estimate.
(4)
Iteration: step 2 and step 3 are repeated until the changes in parameters after each iteration are within a specified tolerance level.

The above steps ensure that the log likelihood function of the observed data increases at every step. So the EM algorithm is guaranteed to converge to some maximum of the likelihood function [15]. The convergence performance under general conditions is given in Wu [27]. The flowchart of the algorithm is shown in Figure 2.

4.2. Formulation of the Multiple Model Approach

As mentioned above, if we compute the Q-function, p(C_obs, C_mis | Θ) should be derived at first using the probability chain rule:

(7)

Using the Bayesian theory, the joint probability density function such as the first term of (7) can be written as

(8)

Similarly, the model identity I_k can be determined from (5), so the second term of (7) can be simplified as

(9)

The derivation of the third term in (7) is based on the chain rule and the assumption that the scheduling variable w_k is known a priori and independent of the past observations as well as the model parameters. Based on the fact that most of the chemical plants predesign the operating points, namely, scheduling variable, p(W∣U, T_1:M, Θ) is derived as

(10)

Then we can substitute (8), (9), and (10) into (7), and the joint probability density of the likelihood of the full data set can be rewritten as

(11)

where

(12)

The expectation of the complete data in the procedure of the EM algorithm is

(13)

From (13) we need to compute the following probability density function:

(1)
log⁡p(y_k∣x_k, Θ_i),
(2)
p(I_k = i∣w_k, T_1:M, o_i),
(3)
,

where p(y_k∣x_k, Θ_i) is calculated by

(14)

(15)

p(I_k = i∣w_k, T_1:M, o_i) is given by (5).

The last probability density function to be calculated denotes the conditional probability that the kth data point comes from the ith local model and can be derived from the Bayesian rule:

(16)

4.3. The Summary of the Identification Procedure

Now we give the identification procedure under the frame of the EM algorithm as follows.

(1) Initialization. Set the initial value of parameters to be estimated.

(2) E-step. Using the current parameter Θ^old, calculate , where p(I_k = i | w_k, T_1:M, o_i) can be computed by (5) and log⁡p(y_k | x_k, Θ_i) is calculated from (15).

(3) M-step. Based on the three terms of the function Q(Θ | Θ^old), only the term as (15) depends on the local model parameter θ_i and the process noise variance σ². Derivative is taken over this term with respect to θ_i and σ², respectively. So the new parameter estimation can be calculated as follows:

(17)

As a result, the new θ_i of the ith ARX local model and σ² are equal to

(18)

(19)

For the local model validity width o_i, i = 1,2, …, M, due to the usage of exponential function, it cannot be calculated from an analytical form directly. The optimization problem searching for the optimal value of o_i can be expressed as

(20)

(21)

Here a nonlinear numerical optimization is required to obtain the optimal o_i between the o_min⁡ and o_max⁡. A constrained nonlinear optimization function named “fmincon” in optimization toolbox of “Matlab” is adopted to search for the optimal o_i at each of the iteration steps [15].

(4) Iteration. Repeat step (2) and step (3), until the converge condition is satisfied. Here the converge condition is defined as the changes of the estimated value between two iterations which are as small as the level 10⁻⁶.

5. A Distillation Column Simulation

Nonlinear system identification is much more complex than linear system identification. In this section, a high purity distillation column is used to test the performance of the multiple model approach based on the EM algorithm.

It has been shown that the purer the products get, the more nonlinear the system becomes [20]. A distillation column is also a typical example for a MISO system in which there are strong interactions between the variables. In this paper, choosing LV-configuration is motivated by the fact that the LV-configuration is the most commonly used in industrial practice.

Here, the process input variables available for control purpose are the reflux (LT) and the boil-up rate (VB). The top product composition (yD) variable is the output. The disturbances to a distillation column can come from many sources. Besides the two manipulated variables, they can come from the feed (feed rate and feed composition), from the pressure inside the column and from the cooling water, and so forth. The distillation column is very sensitive to the feed rate disturbance. The feed rate is assumed to be measurable; therefore, its effect can be incorporated in the EM algorithm. In this paper, the feed rate F is treated as the scheduling variable [23]. When the column is operated over a relatively wide operating region instead of at a single set point, it reveals a significant nonlinear behaviour.

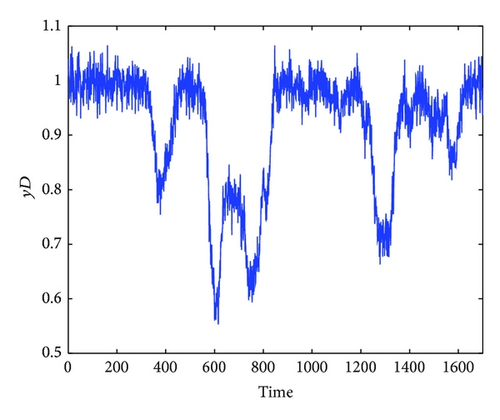
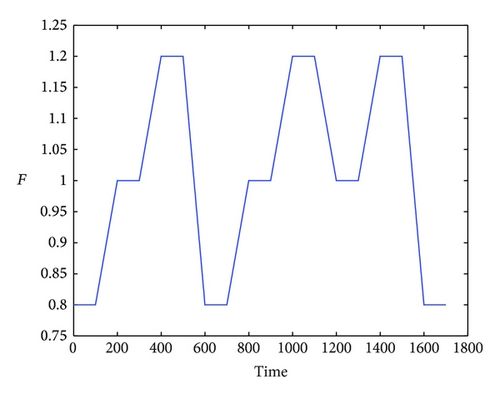
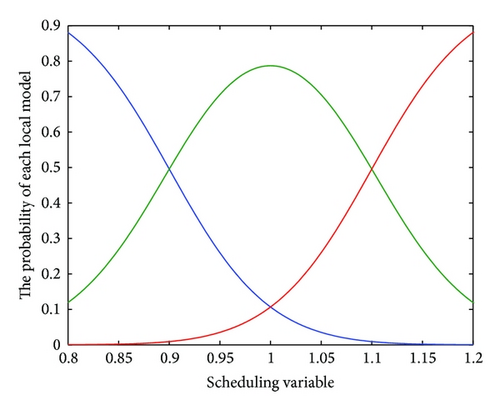
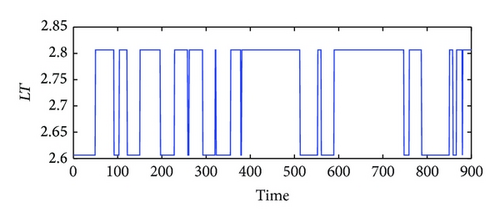
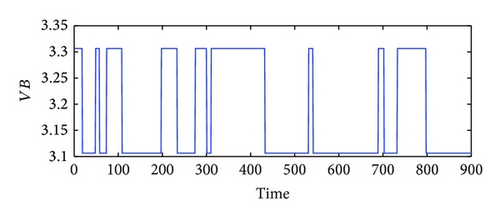
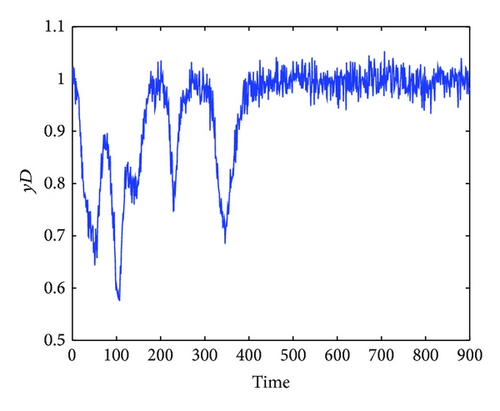
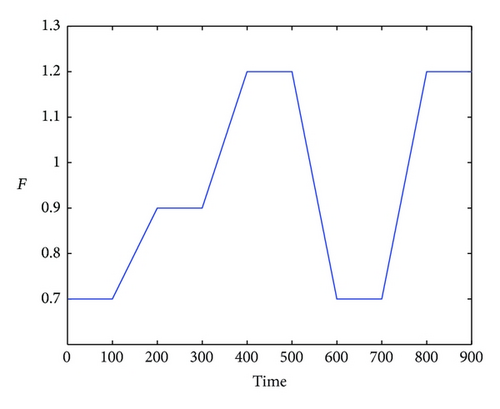
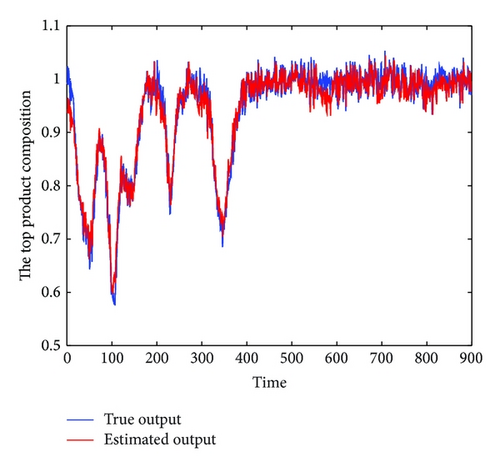
In the simulation, white noise with a variance of 0.05 is added in the simulated output data for unknown process noise. The observed input and output data for the high purity distillation column are shown in Figures 3 and 4. The scheduling variable is designed with three operating points at 0.8 kmol/min, 1.0 kmol/min, and 1.2 kmol/min, respectively, which were given in Figure 5. In order to achieve high identification performance the random binary excitation signals with small magnitude are added in the input variables. The feed rate increases by a fixed step size and no additional excitation signal is added. Then applying the multiple model modeling approach and using the EM algorithm to estimate the parameters of each local model, the simulation results of self-validation tests indicate the efficiency of the proposed method. The comparison and the weighting function curve are given in Figures 6 and 7.

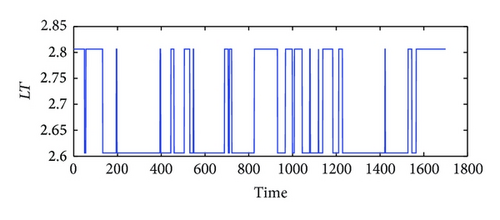
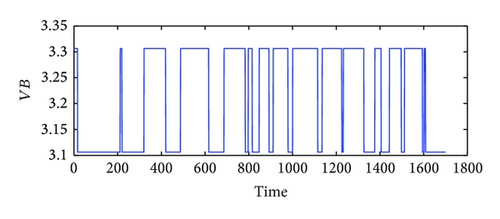
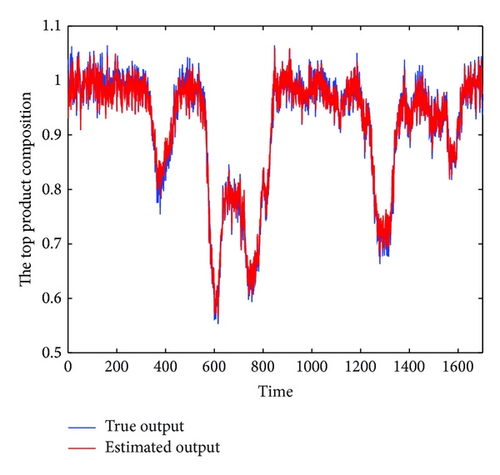
To further test the performance of the identified multiple model, the cross-validation is also carried on the case. The data used for cross-validation as shown in Figures 8 and 9 are generated under different feed rates from Figure 5. Two different operating points are selected in the cross-validation simulation as in Figure 10. It can be seen from Figure 11 that the real process data and the model prediction are in good agreement with each other which effectively confirms the efficiency of the proposed algorithm.

6. Conclusions

A multiple model modeling algorithm based on EM algorithm is proposed and applied for a high purity distillation column reaction process. Taking a full consideration of the dynamic, nonlinearity, and complexity, the parameters of each local model are identified under different operating points. The global model can be obtained by using a weighting function, which adopts an exponential form about scheduling variable under the framework of EM algorithm. Simulation results show that the fusion model of multiple models based on the EM algorithm is very effective in the chemical process of a high purity distillation column.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

The authors thank the financial support by the National Natural Science Foundation of China (nos.: 21206053, 21276111, and 61273131) and the paper is partly supported by the 111 Project (B12018), the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD), the Fundamental Research Funds for the Central Universities (JUDCF10064), and Jiangsu Innovation Program for Graduates (CXZZ11_0464).

References

1 Ljung L., System Identification: Theory for the User, 1987, Prentice Hall.
PubMed Google Scholar
2 de Assis A. J. and Maciel Filho R., Soft sensors development for on-line bioreactor state estimation, Computers and Chemical Engineering. (2000) 24, no. 2–7, 1099–1103, 2-s2.0-0034661658, https://doi.org/10.1016/S0098-1354(00)00489-0.
10.1016/S0098-1354(00)00489-0
CAS Web of Science® Google Scholar
3 Glassey J., Ignova M., Ward A. C., Montague G. A., and Morris A. J., Bioprocess supervision: neural networks and knowledge based systems, Journal of Biotechnology. (1997) 52, no. 3, 201–205, 2-s2.0-0030994705, https://doi.org/10.1016/S0168-1656(96)01645-8.
10.1016/S0168-1656(96)01645-8
CAS PubMed Web of Science® Google Scholar
4 Yan W., Shao H., and Wang X., Soft sensing modeling based on support vector machine and Bayesian model selection, Computers and Chemical Engineering. (2004) 28, no. 8, 1489–1498, 2-s2.0-2342567014, https://doi.org/10.1016/j.compchemeng.2003.11.004.
10.1016/j.compchemeng.2003.11.004
CAS Web of Science® Google Scholar
5 Rasmussen C. E. and Williams C. K. I., Gaussian Processes for Machine Learning, 2006, MIT Press, Cambridge, Mass, USA, MR2514435.
Google Scholar
6 Wang X., Chen J., Liu C., and Pan F., Hybrid modeling of penicillin fermentation process based on least square support vector machine, Chemical Engineering Research and Design. (2010) 88, no. 4, 415–420, 2-s2.0-77951296145, https://doi.org/10.1016/j.cherd.2009.08.010.
10.1016/j.cherd.2009.08.010
CAS Web of Science® Google Scholar
7 Smith R. M., Multiple Model Approaches to Modeling and Control, 1997, Taylor and Francis, London, UK.
Google Scholar
8 Shamma J. S. and Athans M., Guaranteed properties of gain scheduled control for linear parameter-varying plants, Automatica. (1991) 27, no. 3, 559–564, https://doi.org/10.1016/0005-1098(91)90116-J, MR1104514, ZBL0754.93022.
10.1016/0005-1098(91)90116-J
Web of Science® Google Scholar
9 Rugh W. J. and Shamma J. S., Research on gain scheduling, Automatica. (2000) 36, no. 10, 1401–1425, https://doi.org/10.1016/S0005-1098(00)00058-3, MR1829765, ZBL0976.93002.
10.1016/S0005-1098(00)00058-3
Web of Science® Google Scholar
10 Zhu Y. and Xu Z., A method of LPV model identification for control, Proceedings of the 17th World Congress of the International Federation Automatic Control, 2008, Seoul, Republic of Korea, 5018–5023.
Google Scholar
11 Xu Z., Zhao J., Qian J., and Zhu Y., Nonlinear MPC using an identified LPV model, Industrial and Engineering Chemistry Research. (2009) 48, no. 6, 3043–3051, 2-s2.0-64749104394, https://doi.org/10.1021/ie801057q.
10.1021/ie801057q
CAS Web of Science® Google Scholar
12 Zhao Y., Huang B., Su H., and Chu J., Prediction error method for identification of LPV models, Journal of Process Control. (2012) 22, no. 1, 180–193, 2-s2.0-84655162775, https://doi.org/10.1016/j.jprocont.2011.09.004.
10.1016/j.jprocont.2011.09.004
CAS Web of Science® Google Scholar
13 Huang J., Ji G., Zhu Y., and Bosch P., Identification of multi-model LPV models with two scheduling variables, Journal of Process Control. (2012) 22, no. 7, 1198–1208.
10.1016/j.jprocont.2012.05.006
CAS Web of Science® Google Scholar
14 Chen L. and Liu F., Recursive parameter identification for fermentation processes with the multiple model technique, Applied Mathematical Modelling. (2012) 36, no. 5, 2275–2285, https://doi.org/10.1016/j.apm.2011.08.021, MR2878184, ZBL1243.93072.
10.1016/j.apm.2011.08.021
Web of Science® Google Scholar
15 Jin X., Huang B., and Shook D. S., Multiple model LPV approach to nonlinear process identification with em algorithm, Journal of Process Control. (2011) 21, no. 1, 182–193, 2-s2.0-78751575535, https://doi.org/10.1016/j.jprocont.2010.11.008.
10.1016/j.jprocont.2010.11.008
CAS Web of Science® Google Scholar
16 Deng J. and Huang B., Identification of nonlinear parameter varying systems with missing output data, American Institute of Chemical Engineers Jouranl. (2012) 58, no. 11, 3454–3467.
10.1002/aic.13735
CAS Google Scholar
17 Chen L., Tulsyan A., Huang B., and Liu F., Multiple model approach to nonlinear system identification with an uncertain scheduling variable using EM algorithm, Journal of Process Control. (2013) 23, no. 10, 1480–1496.
10.1016/j.jprocont.2013.09.013
CAS Web of Science® Google Scholar
18 Truong H. S., Ismail I., and Razali R., Fundamental modeling and simulation of a binary continuous distillation column, Proceedings of the International Conference on Intelligent and Advanced Systems (ICIAS ′10), June 2010, Kuala Lumpur, Malaysia, 1–5, 2-s2.0-79952769139, https://doi.org/10.1109/ICIAS.2010.5716218.
10.1109/ICIAS.2010.5716218
Google Scholar
19 Bloemen H. H. J., Chou C. T., Van den Boom T. J. J., Verdult V., Verhaegen M., and Backx T. C., Wiener model identification and predictive control for dual composition control of a distillation column, Journal of Process Control. (2001) 11, no. 6, 601–620, 2-s2.0-0035546342, https://doi.org/10.1016/S0959-1524(00)00056-1.
10.1016/S0959-1524(00)00056-1
CAS Web of Science® Google Scholar
20 Bǎieşu A.-S., Modeling a nonlinear binary distillation column, Control Engineering and Applied Informatics. (2011) 13, no. 1, 49–53, 2-s2.0-79957941114.
Web of Science® Google Scholar
21 Luyben W. L., Derivation of transfer functions for highly nonlinear distillation columns, Industrial and Engineering Chemistry Research. (1987) 26, no. 12, 2490–2495, 2-s2.0-0023537571.
10.1021/ie00072a017
CAS Web of Science® Google Scholar
22 Fuentes C. and Luyben W. L., Control of high-purity distillation columns, Process Design and Development. (1983) 22, no. 3, 361–366, 2-s2.0-0020781908.
10.1021/i200022a004
CAS Google Scholar
23 Ravi Sriniwas G., Arkun Y., Chien I.-L., and Ogunnaike B. A., Nonlinear identification and control of a high-purity distillation column: a case study, Journal of Process Control. (1995) 5, no. 3, 149–162, 2-s2.0-0029322696.
10.1016/0959-1524(95)97302-9
Web of Science® Google Scholar
24 Skogestad S., Dynamics and control of distillation columns: a tutorial introduction, Chemical Engineering Research and Design. (1997) 75, no. 6, 539–562, 2-s2.0-0031228960.
10.1205/026387697524092
CAS Web of Science® Google Scholar
25 McLachlan G. J. and Krishnan T., The EM Algorithm and Extensions, 2008, Second edition, John Wiley & Sons, Hoboken, NJ, USA, https://doi.org/10.1002/9780470191613, MR2392878.
10.1002/9780470191613
Google Scholar
26 Raghavan H., Tangirala A. K., Gopaluni R. B., and Shah S. L., Identification of chemical processes with irregular output sampling, Control Engineering Practice. (2006) 14, no. 5, 467–480, 2-s2.0-30744439044, https://doi.org/10.1016/j.conengprac.2005.01.015.
10.1016/j.conengprac.2005.01.015
Web of Science® Google Scholar
27 Wu C.-F. J., On the convergence properties of the EM algorithm, The Annals of Statistics. (1983) 11, no. 1, 95–103, https://doi.org/10.1214/aos/1176346060, MR684867, ZBL0517.62035.
10.1214/aos/1176346060
PubMed Web of Science® Google Scholar

Citing Literature

All articles

Multiple Model Identification for a High Purity Distillation Column Process Based on EM Algorithm

Abstract

1. Introduction

2. Description of a High Purity Distillation Column

3. Problem Formulation Using Multiple Model Method

4. The ARX Model Identification under the EM Algorithm

4.1. The EM Algorithm Review

4.2. Formulation of the Multiple Model Approach

4.3. The Summary of the Identification Procedure

5. A Distillation Column Simulation

6. Conclusions

Conflict of Interests

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Multiple Model Identification for a High Purity Distillation Column Process Based on EM Algorithm

Abstract

1. Introduction

2. Description of a High Purity Distillation Column

3. Problem Formulation Using Multiple Model Method

4. The ARX Model Identification under the EM Algorithm

4.1. The EM Algorithm Review

4.2. Formulation of the Multiple Model Approach

4.3. The Summary of the Identification Procedure

5. A Distillation Column Simulation

6. Conclusions

Conflict of Interests

Acknowledgments

References

Citing Literature

Figures

References

Related

Information