Dynamic Pricing Based on Strategic Consumers and Substitutes in a Duopoly Setting
Abstract
Based on the rational strategic consumers, we construct a dynamic game to build a two-period dynamic pricing model for two brands of substitutes which are sold by duopoly. The solution concept of the dynamic game is Nash equilibrium. In our model, consumers have been clearly segmented into several consumption classes, according to their expected value of the products. The two competing firms enter a pricing game and finally reach the state of Nash equilibrium. In addition, decision-making process with only myopic consumers existing in the market is analyzed. To make the paper more practical and realistic, the condition, in which the myopic and strategic consumers both exist in the market, is also considered and studied. In order to help the readers understand better and make it intuitively more clearly, a numerical example is given to describe the influence of the main parameters to the optimal prices. The result indicates that, to maintain the firms’ respective optimal profits, the prices of the products should be adjusted appropriately with the changes of product differentiation coefficient.
1. Introduction
Pricing and product differentiation are among the most important strategies for firms in the competitive product market. In order to increase profits, the manufactures usually apply various strategies, including selling their products in several periods.
Dynamic pricing, which means that product prices are changed periodically over time to maximize revenue, are widely applied in product market. It has received considerable attention in research and application in recent years. The benefits of dynamic pricing methods have been known in some relatively stable industries, such as airlines, hotels, and electric utilities, where the capacity is fixed in the short term and perishable. Recently, an increasing adoption of dynamic pricing methods in retail and other industries appears. Elmaghraby and Keskinocak [1] thought that three factors contributed to this phenomenon: (1) the increased availability of demand data; (2) the ease of changing prices due to new technologies; and (3) the availability of decision-support tools for analyzing demand data and dynamic pricing.
Determining the optimal prices in different periods requires the decision maker to know not only his own operating costs and the supply ability, but also how much the customers value the products and what the future demand will be. Thus, to charge a customer the right price, a company must get a wealth of information about its customer base and its competitor and also be able to set and adjust its prices at the minimal cost. Until recently, a certain amount of papers has done some research on dynamic pricing in various aspects, such as the quantity of manufactures and products, different categories of goods, and even taking inventory into account. Mitra [2] constructed a dynamic pricing model for different quality remanufactured goods in order to reach the maximum profits. Feng and Gallego [3] discussed a dynamic pricing problem of multiproducts. Federgruen and Heching [4] discussed the pricing and inventory strategy in the condition of uncertain demand. The current paper focuses on the dynamic pricing mechanisms for two brands of substitutes which are sold by duopoly with the condition that strategic consumers exist in the market.
Product differentiation is an effective way for firms to occupy the market share and increase firm’s profits in a competitive market. And the strategy of product differentiation has been prevalent in many areas of our society, such as food products, electronics, and even aviation industry. In the aspect of pricing, firms in many industries often adjust their strategies to vary prices over time in order to better manage demand and increase profits. When making pricing decisions, a firm should take both the strategies of substitutes produced by their competitors and the same products sold in different cycles into consideration.
Product differentiation in the markets is often complicated by the fact that decision processes for the market participants are intrinsically dynamic. In economics and marketing, product differentiation (also known simply as differentiation) is the process of distinguishing a product offered by others and making it more attractive to a particular target market. This involves differentiating it from competitors’ products as well as a firm’s own goods offerings. The concept was proposed by Chamberlin [5] in his Theory of Monopolistic Competition. One manufacture’s products are considered as the substitutes of its competitors’ products. However, most durable goods are sold in several periods, so the same goods sold in different selling cycles are also regarded as substitutes. A related problem was considered by Liu and Van Ryzin [6]. They studied a two-period model with strategic consumers and quantity decisions (rather than pricing) being taken into consideration. And the model was applied to induce early purchases.
Consumer choice models are studied extensively in the marketing literature. A survey of consumer choice and strategic behavior models in retail management is found from the paper of Shen and Su [7]. The heterogeneity of consumers in the market determines that different customers have disparate valuation of different products. Consumers employ a variety of consumption patterns with actions that vary in time, even for a single brand of goods. In terms of their various psychology and behavioral characteristics, the consumers are divided into two types: myopic versus strategic customers. Elmaghraby and Keskinocak [1] had done some research on dynamic pricing in the presence of inventory considerations. They put forward a detailed expression of the two types of customers: “The purchasing behavior of the customers affects the seller’s pricing decisions over time. A myopic customer is the one who makes a purchase immediately if the price is below his/her valuation (reservation price), without considering future prices. Myopic (or nonstrategic) customer’s behavior allows the seller to ignore any detrimental effects of future price cuts on current customer purchases. Conversely, a strategic (or rational) customer takes into account the future path of prices when making purchasing decisions. Dynamic pricing decisions of a seller faced strategic customers is more complex, for the sake that the seller has to consider the effects of future and current prices on customers’ purchasing decisions.”
Although it seems that most of the ingredients in our model have been studied, one of the distinctive features and the innovation point of this paper is that it explores, in a unified model, all strategic interactions, and we combined the strategies into a special marketplace. In such a market circumstance, two competing firms sell products to a finite population of consumers in two selling periods, and each firm sells only one type of products. What is more, we also bring forth new ideas, in which all the situations of how consumers exist in the market are considered. A very important point, what our model distinguishes from others, is that it provides a dynamic game for duopoly and solved by Nash equilibrium, which is more easily understood. And this point is our core innovation. Through the analysis and simulation of our model, we derived the optimal price strategies for both firms expressed in the form of mathematical model. Executing these strategies is beneficial to both sides including the consumers. Furthermore, this framework allows us to adopt more realistic assumptions and accommodate it to the real economic market. Some of the papers we reviewed about dynamic pricing in product market setting considered only a single product, while several papers in our research studied the condition that only one manufacture exists, and their focus is mainly on static product line pricing, not dynamic pricing [8]. We hope to relax some of these limitations in our subsequent work.
The remainder of the paper proceeds as follows. In the next section, we introduce the model in a general context, and we spell out the method and hypothesis of the model. We then show in Section 3 the concept of the solution and the optimal dynamic prices are derived and presented. In the same section we also illustrate two general conditions: special condition with only myopic consumers existing in the market and myopic consumers and strategic consumers existing in the market in a certain proportion θ. In Section 4, the intuitive numerical simulation is examined in this part. We summarize our main findings of this work and outline new directions for further research in the last section. Proofs of proposition and the optimal profits are found in Appendix A.
2. Problem Descriptions and Concept of Pricing Model
With the progress of the society and the rapid development of economy, commodities in the market are stepping forward to the direction of diversification. The version, design, and even generation of the same product are changing constantly, especially in the phone market. However, facing the diversification of products, consumers are also becoming more rational and strategic. This kind of phenomenon is very common in the mobile industry. Suppose you are a potential mobile phone consumer and you want to choose one from Samsung and iPhone. As we all know, updating speed of them is faster. So you will face several choices: purchasing Samsung or iPhone, purchasing one in the current generation of them or the later one. Then the decision problem appears. The manufacturers will also have to make certain pricing sales strategies due to this reality.
2.1. Products
There are two potential brands of goods, A and B, on the market, which are substitutes for each other, and they are quality-differentiated products. Two manufactures produce and sell the products A and B in two periods, respectively. We assume that brand A is produced by firm M1 and brand B is produced by firm M2. At the steady limit, firm M1 and M2 play a pricing game and eventually converge to Nash equilibrium. The duopoly faces no capacity constraints. All goods of each brand are of equal quality and sold in two periods: the product in the second period is sold at discount while the one in the first period is sold at normal price.
2.2. Consumers
As we have declared above, the consumers are assumed to be rational and strategic. They will make purchasing decisions based on the consumer surplus maximization conditions.
2.3. Manufacturers: M1 and M2
We assume that brand A is produced by firm M1 and brand B is produced by firm M2. The manufacturers face no capacity constraints; in other words, the products are ample for the market. The fixed costs are ignored, which they have no effect on our model and marginal costs for brands A and B are denoted by cA and cB, respectively, subject to the constraint cA≻cB≻0, in which the left inequality is due to the different quality and brand, while the right is obvious. In the first sales cycle, the prices of products A and B are defined by and , obviously, , and in the second period, the prices of the two brands can be shown as and with the constraint . In the above context, we have presumed that, in the second sales cycle, the manufacturers will sell their products at discount, so , are easily verified.
2.4. Concept of the Pricing Model
3. Dynamic Pricing Based on Our Model
Our model includes two dynamic game problems. Consumers who are price takers, play the game strategically against the producers, while the manufacturer plays the game strategically against the consumers and the other producer. The manufacturers make their pricing decisions in view of consumers’ strategic behaviors. This is a two-period dynamic pricing game, in which consumers with high valuation will purchase goods in the first period but not the second one, and the ones who have a comparatively low valuation will not purchase a commodity at a high price in the first selling cycle. On the other hand, as in any standard game, all the players in our model are assumed to be rational and to maximize their own values. In our research, the two manufacturers play in a dynamic pricing game to pursue the maximum profits.
According to the above context, we know that the consumers with the highest valuation will acquire A in the first period, and the ones with the lowest valuation will obtain B in the later cycle; however, the rest of them between the highest and the lowest have two choices: purchasing A in the second period or B in the first cycle, which is determined by the magnitude of the two parameters λ and δ1. Owning to the constraints 0≺λ≺1, 0≺δ1≺1, we divide them into two kinds of situations to carry on the analysis, 0≺λ≺δ1≺1, 0≺δ1≺λ≺1.
3.1. The Condition 0≺λ≺δ1≺1
The present analysis shows that , , , and , in the condition 0≺λ≺δ1≺1. We easily verify that . In other words, the valuation of A in the second period is higher than B in the first sales cycle, and then ordering of consumer choice is A1, A2, B1, and B2.
According to the above inequalities (5), (6), and (7), we can easily work out the class-division points and show the consumers’ different purchasing states of diverse products in different cycles clearly; in addition, the market shares of substitutes are figured out (See Table 1).
| Valuation | Purchasing states | Market share |
|---|---|---|
| v1 ≤ v≺U | A1 | N(U − v1)/U |
| v2 ≤ v≺v1 | A2 | N(v1 − v2)/U |
| v3 ≤ v≺v2 | B1 | N(v2 − v3)/U |
| v4 ≤ v≺v3 | B2 | N(v3 − v4)/U |
| 0 ≤ v≺v4 | — | — |
Consumers’ purchasing states are displayed in Figure 1.

3.2. The Condition 0≺δ1≺λ≺1
According to the theory in the former condition, we figure out the consumers’ strategic patterns and the market shares following this condition (See Table 2).
| Valuation | Purchasing states | Market share |
|---|---|---|
| v1 ≤ v≺U | A1 | N(U − v1)/U |
| v2 ≤ v≺v1 | B1 | N(v1 − v2)/U |
| v3 ≤ v≺v2 | A2 | N(v2 − v3)/U |
| v4 ≤ v≺v3 | B2 | N(v3 − v4)/U |
| 0 ≤ v≺v4 | — | — |
3.3. The Optimal Pricing Strategy
As we have stated in the above context, all the players in our model are assumed to be rational and maximize their own values, so as to the manufacturers. They pursuit their own profits maximization, with the common market constraints satisfied. Trade among a group of rational actors would reach a stable state if no individual had anything further to gain by making a new trade. In our model, this means that the steady limit will be the condition in which the two producers both reach their optimum. Obviously, it is a dynamic pricing game and the Nash equilibrium is then the intersection of these best responses.
To solve the Nash equilibrium, we need to find best responses with constraints appropriately imposed for both firms.
Let us sum up, finding the equilibrium solution of the above two cases amounts to solve various profit functions, defined in (13), (14) with the inequalities (10) and (12) as constraints in the whole sales cycle.
Proposition 1. Based on the analysis above, optimal pricing strategy of the manufactures in the condition 0≺λ≺δ1≺1 is interior solutions given by
The optimal profits of the two firms are too trivial and given in Appendix B.
Proposition 2. The condition is 0≺δ1≺λ≺1.
It is easy to verify that the Hesse matrix is negative definite. As the same reason as the first condition, the optimal pricing strategy is worked out. As analysis above, the prices of the two products in two selling cycles are figured out, and the functions of M1 and M2 profits are also given; then the profits are easily derived straightforwardly at least using some software packages such as Mathematica. The concept and method are absolute the same to Proposition 1 and we know that these expressions are too long and are not particularly revealing; we do not show them up.
3.4. Special Condition with Pure Myopic Consumers in the Market
From the above analysis, we assume that the consumers in a realistic market are all rational and strategic. Now we shift our hypothesis to the condition that only myopic consumers exist in the market and figure out the methods of optimal pricing strategies for two manufacturers straightforwardly. The concept of our model is as follows.
As the same theory as Propositions 1 and 2, according to the Kuhn-Tucker conditions, we reach the outcomes (the optional prices and profits) directly.
3.5. Myopic Consumers and Strategic Consumers Exist in the Market in a Certain Proportion θ
Some consumers employ a variety of consumption patterns with actions that vary in time; we call them strategic consumers, while others may only take the current period into account, and they are myopic consumers. Everyone knows that no pure market exists, and the same method applies to the consumer market. So we suppose a ratio θ exists between the quantities of myopic consumers and strategic consumers.
4. Numerical Example and Discussions
On account of the mathematical model established in the above paragraphs, we figure out that the optimal price has a certain sensitivity of each parameter in the model abstractly. In this section, we will illustrate the sensitivity through a numerical example so as to the slight change to be found out obviously.
Proposition 3. In this paper, we assumed that the total number of consumers in the market is one hundred (N = 100). The maximum expect valuation of consumers is ten (U = 10). The cost of product A(B) is five (four) (cA = 5, cB = 4). In this section we check the changes and figure out the sensitivity of the prices when λ varies with fixed δ1 = δ2 = 0.8 and cA = 5, cB = 4.
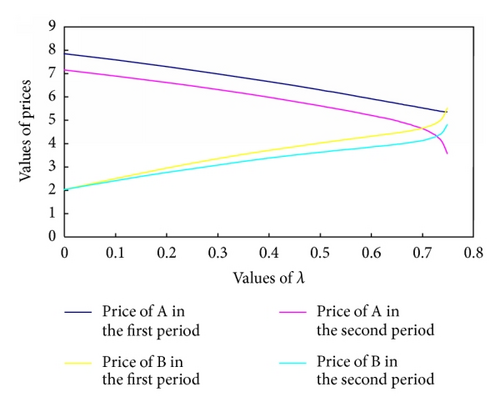
λ represents the difference of two different goods A and B, while δ stands for preference difference of purchasing the same product in two different periods. The detailed prices vary as functions of λ with δ fixed are displayed in Figure 2. From Figure 2, we can see that, with the increase of λ, the four price curves changed greatly. As we know, this parameter which is becoming more and more close to 1 indicates that the differentiation between the two kinds of products is becoming smaller. Then the prices between A and B are getting closer to each other, with and getting down but and going up. If λ is infinitely close to δ, it means that consumers have nearly the same preference for product B in the first period and A in the later. And the price curves intersect here. In another aspect, obviously, is always larger than . That is because the consumer preferences on the first phase of products are greater than the goods of the second stage. With the increase of λ, the quality of product B made by manufacture M2 is getting closer to A produced in manufacture M1. Consumer preferences for B will enhance. If M1 does not reduce the price of A, then more and more consumers will turn to buy B. So in order to keep the profit maximization that all the manufactures will pursue and ensure a certain customers, M1 has to adjust the prices with the optimal prices curves. Since with the continuous improvement of product quality of B, more and more consumers increase their preference for B, the same reason of pursing profit maximization, M2 will raise prices of its products as Figure 2 shows.
From this figure, we can say that λ has a great influence on the interactions of two manufactures. Also, to combine the practical situation of realistic market, we can see that the trends of the four prices curves are consistent with the market competition environment in realistic society.
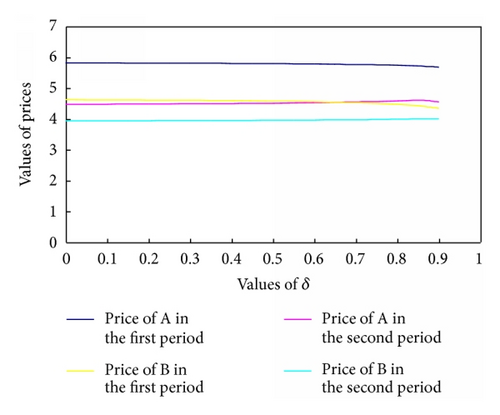
The same theory, for the purpose of having a quantitative perception on how these optimal prices are arranged on the δ-plane, we graphically display it in Figure 3. As we have already assumed, λ is fixed, and the variation of δ does not influence the interaction of product priced of two companies. Unlike the above graph, the curves variation in Figure 3 is relatively weak. However, the trend is also the same. From here, we can derive a small conclusion that differentiation of the same products sold in two phases should be smaller than different product differentiation. As δ increases, the gaps of the same products sold in the first stage and the second selling cycle are becoming smaller. If δ approaches to 1, it implies the consumers’ preferences stand more stable. In other words, buying goods in different cycles does not make huge differences on consumers’ decision. If δ stays away from 1, which means that the gaps of one type of goods sold in different selling cycles are large, in the competitive context, to pursue the maximize profits, each manufacture has to reduce the product prices in the second stage, just like the gaps of and shown in Figure 3. And, with the increase of δ, the companies have to narrow the price gaps for more customers.
5. Conclusions and Further Research
- (1)
Construct different consumer surplus function for different products and profit functions for two competing manufacturers and we work out the different consumer purchasing decisions and the optimal prices for firms in the market.
- (2)
Through the numerical simulation, we show the sensitivity of optimal prices and decisions with respect to valuation parameters. Then we easily find out how these valuation parameters influence the pricing decision.
- (3)
Despite the fact that most of the consumers are strategic, we also analyze the special condition that only myopic consumers exist in the market. What is more, we proposed an assumption that myopic consumers and strategic consumers exist in the market with a certain proportion θ.
- (4)
Our paper is based on the previous studies but the innovation point is that the two kinds of product are produced in two different manufactures, and the Nash equilibrium will be our steady state.
Through the above conclusion, we have made some progress in this area based on previous research. However, there also exist some limitations in our paper. First of all, even in duopoly setting, we can make our model somewhat more realistic by extending the selling cycle to three or more just like the generation of iPhone. Secondly, in this paper, we just take two substitutes into consideration. As in the fact, when purchasing an item, one usually will face more than two choices, and these are all substitutes, so we can also introduce more substitute products to be more realistic. Thirdly, confronting the model with empirical data could be another limitation of our paper. In our paper, we analyzed the model and simulation with only experimental data and mathematical model. So many extensions of our model can be envisioned. And a lot work in this area deserves the effort.
Conflict of Interests
The authors declare that there is no conflict of interests regarding the publication of this paper.
Acknowledgments
The financial supports from National Natural Science Foundation of China (Grant nos. 71171181, 71322101, 71271195, and 71110107024), Chinese Ministry of Education (NCET-10-0993), and USTC Foundation for Innovative Research Team (WK2040160008) are acknowledged.
Appendices
A. Proof of Proposition 1
Based on the equations given above, the closed-form expressions for all interesting quantities, such as the equilibrium prices, market, and the manufacture’s profits, can be derived straightforwardly, using some software packages that can perform symbolic manipulation such as Mathematica.
Solving the two Lagrange equations we can easily get the optimal prices of the four kinds of products and profits of the two firms.




