International Journal of Computational Mathematics

Volume 2014, Issue 1 659675

Research Article

Open Access

Modelling Hepatotoxicity of Antiretroviral Therapy in the Liver during HIV Monoinfection

Corresponding Author

Hasifa Nampala

[email protected]

Department of Mathematics, Faculty of Science Education, Busitema University, P.O. Box 236, Tororo, Uganda busitema.ac.ug

Search for more papers by this author

Livingstone S. Luboobi,

Livingstone S. Luboobi

Department of Mathematics, School of Physical Sciences, College of Natural Sciences, Makerere University, P.O. Box 7062, Kampala, Uganda mak.ac.ug

Search for more papers by this author

Joseph Y. T. Mugisha,

Joseph Y. T. Mugisha

Department of Mathematics, School of Physical Sciences, College of Natural Sciences, Makerere University, P.O. Box 7062, Kampala, Uganda mak.ac.ug

Search for more papers by this author

Celestino Obua,

Celestino Obua

Department of Pharmacology and Therapeutics, College of Health Sciences, Makerere University, P.O. Box 7062, Kampala, Uganda mak.ac.ug

Search for more papers by this author

Hasifa Nampala,

Corresponding Author

Hasifa Nampala

[email protected]

Department of Mathematics, Faculty of Science Education, Busitema University, P.O. Box 236, Tororo, Uganda busitema.ac.ug

Search for more papers by this author

Livingstone S. Luboobi,

Livingstone S. Luboobi

Department of Mathematics, School of Physical Sciences, College of Natural Sciences, Makerere University, P.O. Box 7062, Kampala, Uganda mak.ac.ug

Search for more papers by this author

Joseph Y. T. Mugisha,

Joseph Y. T. Mugisha

Department of Mathematics, School of Physical Sciences, College of Natural Sciences, Makerere University, P.O. Box 7062, Kampala, Uganda mak.ac.ug

Search for more papers by this author

Celestino Obua,

Celestino Obua

Department of Pharmacology and Therapeutics, College of Health Sciences, Makerere University, P.O. Box 7062, Kampala, Uganda mak.ac.ug

Search for more papers by this author

First published: 19 October 2014

https://doi.org/10.1155/2014/659675

Citations: 3

Academic Editor: Baojun Song

Share a link

Email
Wechat
Bluesky

Abstract

Liver related complications are currently the leading cause of morbidity and mortality among human immunodeficiency virus (HIV) infected individuals. In HIV monoinfected individuals on therapy, liver injury has been associated with the use of antiretroviral agents as most of them exhibit some degree of toxicity. In this study we proposed a mathematical model with the aim of investigating hepatotoxicity of combinational therapy of antiretroviral drugs. Therapy efficacy and toxicity were incorporated in the model as dose-response functions. With the parameter values used in the study, protease inhibitors-based regimens were found to be more toxic than nonnucleoside reverse transcriptase inhibitors-based regimens. In both regimens, the combination of stavudine and zidovudine was the most toxic baseline nucleoside reverse transcriptase inhibitors followed by didanosine with stavudine. However, the least toxic combinations were zidovudine and lamivudine followed by didanosine and lamivudine. The study proposed that, under the same second line regimens, the most toxic first line combination gives the highest viral load and vice versa.

1. Introduction

Among people infected with human immunodeficiency virus (HIV), liver related complications have become the leading causes of morbidity and mortality [1]. There are a number of factors identified that are known to contribute to liver related mortality in HIV infected people. These are, for instance, coinfections with viral hepatitis B (HBV) and hepatitis C (HCV) as well as the use of antiretroviral therapy (ART) [2–6]. Although liver disease can occur solely due to HIV infection [7–10], the use of ART is highly associated with end stage liver disease in HIV infected people [6, 11].

A human body identifies every substance it absorbs, including drugs as a foreign substance. All substances that are identified as foreign are subjected to chemical processes, [12], to make them suitable for elimination. Although all tissues in the body have some ability to metabolise, the liver is the central metabolic clearing organ of all chemicals from a human body. This process is carried out by metabolising enzymes cytochrome P450 which are found in hepatocytes [12]. The role played by hepatocytes in handling toxic drug substances makes them vulnerable to drug induced injury (hepatotoxicity) and, consequently, cell death [12–14]. Drug-induced liver injury is responsible for 5% of all hospital admissions and 50% of all acute liver failures [5].

According to [15], generally all antiretroviral drugs exhibit some level of toxicity to the liver. Hepatocytes that are responsible for metabolizing toxic antiretroviral drugs [12, 13] also support all stages of HIV infection and replication [9, 10, 16, 17]. This double distress to hepatocytes would possibly partly explain the progression of liver disease in HIV infected people on ART. Using ART in combination makes it even more complicated to assess which drug leads to higher levels of hepatotoxicity than the other [18].

According to [8, 10, 19], HIV can directly infect human hepatocytes. Considering HIV infection and replication in hepatocytes [16, 17, 20] and CD4+ cells [21–23] as well as macrophages, [11, 19], this study used a mathematical model to analyse therapeutic and toxic effects of HIV antiretroviral therapy. Defining hepatotoxicity generally as liver damage, there are a number of conditions that would fall under hepatotoxicity, and they include hepatitis, hepatic necrosis, and hepatic steatosis [24, 25]. This study considered only hepatic necrosis, which is the death of liver cells.

Drugs studied include zidovudine (AZT), emtricitabine (FTC), didanosine (DDI), lamivudine (3TC), stavudine (d4T), efavirenz (EFV), atazanavir (ATV), and nelfinavir (NFV). Various drug combinations as recommended by World Health Organisation were considered. The study accounted for therapeutic and toxic effects of all classes of ART in form of dose-response functions [26, 27].

2. Material and Methods

2.1. Mathematical Model Development

Recent study by [26] as well as [28] asserts that all classes of ART exhibit dose-response curves. Finding a dose that gives 50% of maximal response is one method of determining how effective the drug is; therefore, [26] recommends that it would be of great contribution if efficacy of ART would be modelled as dose-response.

Much as antiretroviral drugs are taken in doses at specific time intervals and the effectiveness and toxicity of the drug are largely dependent on the pharmacokinetics of the drug taken, our study preferred to use the Hill equation as recommended by [26], to model drug efficacy as opposed to Michaelis-Menten kinetics [29]. Reactions involving a single substrate are often assumed to follow Michaelis-Menten kinetics, irrespective of the model′s underlying assumptions. Since we are dealing with possible multiple drug reactions, the use of Michaelis-Menten equation would thus be inappropriate. The study has also adopted the use of the Hill equation because we are investigating therapeutic and toxic effect of therapy at steady state.

Therapeutic response function is defined as a Hill equation (1) to describe the effectiveness of the drug [26]. Effectiveness of reverse transcriptase inhibitors (RTIs) and protease inhibitors (PIs) are represented, respectively, by drug efficacies ϕ₁ and ϕ₂, where 0 ≤ ϕ₁, ϕ₂ ≤ 1. If the drug is 100% effective, then ϕ₁ = ϕ₂ = 1,

()

where d is the drug dose concentration, IC₅₀ is the drug concentration that leads to 50% of the maximal viral inhibition, and m is the gradient of the dose-response curve. Response is the ability of the drug to inhibit viral replication [28]. Gradients for dose-response curves of HIV drugs are given by [30] and are shown in Table 1.

Table 1. Medication and corresponding parameter values. m and IC₅₀ are from Supplementary Table 1 of [30].

Medication	d [μM]	m	IC₅₀ [μM]	TD₅₀ [μM]	Reference
Zidovudine (AZT)	37.4195	0.85	0.1823	127.7868	[32]
Didanosine (DDI)	28.2229	1.07	0.1794	275.3284	[32]
Lamivudine (3TC)	21.8103	1.15	0.0298	170.5277	[33]
Stavudine (d4T)	4.4603	1.13	0.552	431.6235	[32]
Efavirenz (EFV)	31.6776	1.67	0.0054	53.8520	[34]
Atazanavir (ATV)	7.0932	2.69	0.0136	85.1185	[32]
Nelfinavir (NFV)	62.81	1.81	0.1668	72.8875	[35]

In the process of metabolising toxic ART, some healthy as well as HIV infected hepatocytes get injured/die [12–14]. The toxic effect of ART on hepatocytes is also assumed to be dose-dependent. Thus, infected and healthy hepatocytes are assumed to die during drug metabolism at a rate ψ for 0 ≤ ψ ≤ 1 depending on the drug dose, [26], where ψ is defined as

()

d is the drug dose, TD₅₀ is the dose at which toxicity occurs in 50% of exposed cases, and m is the gradient of the dose-response curve. We assume that both toxic and therapeutic effects of antiretroviral drugs exhibit dose-response curves of relative gradients since both are dose-dependent [31]. Due to scarcity of literature regarding dose-response analysis of ART toxicity, we assume that all the gradients might not be the same but relative. This is based on the assumption that since nonnucleoside reverse transcriptase inhibitors (NNRTIs) and PIs are the most efficacious and have higher gradients than NRTIs, [28, 30], this is consistent with toxicity and hence relative gradients.

In model formulation, we define eight variables as follows: uninfected CD4+ cells (T_c), infectious CD4+ cells (I_c), uninfected hepatocytes (T_h), latently infected hepatocytes (I_hl), [9], productively infected hepatocytes (I_ha), HIV-specific cytotoxic T lymphocytes (L), viral load (V), and the level of enzyme alanine aminotransferase in blood (A).

Model parameters are as follows: CD4+ cells and hepatocytes are produced from within the body at rates λ₁ and λ₂ and die naturally at rates d₁ and d₃, respectively. We assume that, among all cells in the liver, HIV has high affinity for CD4+ cells and hepatocytes [20]. Thus, from the free viral population in the liver, if a virus is to infect a cell, there is a probability q that it will infect a hepatocyte at rate β₂ and a probability 1 − q that it infects a CD4+ T cell at rate β₁. Infected CD4+cells die at rate d₂, where d₂ > d₁, and are cleared by HIV-specific cytotoxic T-lymphocytes (CTLs) at a rate k₁.

When a hepatocyte is infected, there is a probability p that it becomes productively infected (viral replication will take place after successful reverse transcription) and probability (1 − p) that the cell will become latently infected, such that there is no viral production until cell activation. Decay rates for productive hepatocytes and latently infected hepatocytes are, respectively, d₅ and d₄, where d₅ > d₄ [36]. Productively infected hepatocytes are killed by HIV-specific CTLs at rate k₂ and until activated, latently infected hepatocytes will not trigger the action of CTLs. This study assumes that latently infected hepatocytes will either get activated to become infectious or die. There is no possibility that they will become uninfected again [37]. Latently infected hepatocytes are activated at rate μ, and it is assumed that this rate is reduced by the the efficacy of PIs. This is because our study assumed that reverse transcription has already taken place at this stage so reverse transcriptase inhibitors will have no effect.

With or without any pathogen in the body CTLs proliferate naturally at rate x and in the presence of HIV infection, they proliferate at rate k₃ and are cleared at rate d₆. Let s₁ and s₂ represent the rates of HIV production per infected CD4+ cells and productively infected hepatocytes, respectively. In addition to CD4+ cells and hepatocytes, HIV productively infects other cells and macrophages like Kupffer cells in the liver [11, 19, 45]. These cells produce virions at rate m. The study assumed that the effect of medication is translated generally into minimal viral load. Thus, viral production from macrophages is also inhibited by both RTIs and PIs. As in [46], we assumed a synergy additivity of PIs and RTIs as Φ = (1 − ϕ₁)(1 − ϕ₂) [39]. Virions die at a per capita rate d₇.

This study assumes that some infectious hepatocytes that die due to drug metabolism are able to release viral particles, provided that at the point of hepatocyte’s death all the stages of viral production have been attained. N is the per capita rate of virions production by each infectious hepatocyte that dies due to drug metabolism. Viral production due to hepatotoxicity was inhibited by resultant efficacy of both RTIs and PIs.

Equation (10) defines the level of enzyme alanine aminotransferase (ALT) in the blood system. Among other enzymes, hepatocytes contain enzyme ALT, and when the cells die by any means, ALT leaks into the blood where it is clinically detected. According to [3], when there is no infection, the level of ALT in the blood system is generated from naturally dying hepatocytes at rate r. As described in [42], k₄ is the rate at which ALT is generated from hepatocytes that die due to HIV infection. (d₅ + ψ + k₂L) and (d₄ + ψ) are the total death rate of productively infected hepatocytes and latently infected hepatocytes, respectively, attributed to HIV infection. The contribution to ALT by healthy hepatocytes is only due to drug metabolism. ALT is cleared from the blood naturally at rate d₈.

From the assumptions and description above we have the following system of ordinary differential equations:

()

2.2. Model Analysis

2.2.1. Positivity and Boundedness of Solutions

With initial conditions T_h0 > 0, I_c0 > 0, T_h0 > 0, I_hl0 ≥ 0, I_ha0 ≥ 0, L₀ > 0, V₀ > 0, and A₀ ≥ 0, the solutions for T_h, I_c, T_h, I_hl, I_ha, L, V, and A, respectively, remain positive and bounded provided t > 0.

We define N_c and N_h as the total number of CD4+ cells and hepatocytes, respectively, where

()

Given that d₂ > d₁ and d₅ > d₄ > d₃ as in [36] and that all variables and parameters are positive (otherwise the model would not be biologically feasible) then

()

Thus

()

Implying

()

hence

()

where κ is the total number of hepatocytes at the time of infection. Equation (15) indicates that there are two cases to consider:

(1)
consider
()
the upper bound of N_h increases and approaches asymptotically the value λ₂/(ψ + d₃);
(2)
consider
()
the upper bound of N_h decreases and approaches asymptotically the value λ₂/(ψ + d₃).

In either case N_h(t) remains bounded.

Similarly, it can also be shown that N_c(t) is bounded by λ₁/d₁.

If the total number of CD4+ cells (N_c) and hepatocytes (N_h) are bounded by λ₁/d₁ and λ₂/(d₃ + ψ), then the subclasses (I_c) and (I_ha and I_hl) respectively are bounded. Thus, letting M₁ = λ₂/(d₃ + ψ) and M₂ = λ₁/d₁ then T_c < M₂, I_c < M₂, T_h < M₁, I_hl < M₁, and I_ha < M₁.

Using (9) and considering I_c < M₂ and I_a < M₁, then

()

Letting Q = (1 − ϕ₂)s₁M₂ + (1 − ϕ₂)s₂M₁ + (1 − Φ)m, where Q > 0 since 0 ≤ ϕ₁, ϕ₂, Φ ≤ 1. Using the same method as in (15)

()

where V₀ is initial viral load.

Using the same argument as in (15), we can deduce that V is bounded by V₀.

Using (8) and taking only infection-dependent proliferation, on assumption that antigen-independent proliferation is naturally bounded, it can be shown that

()

where s = k₁(M₁ + M₂) − d₅. Letting

, then L < M₄.

Equation (10) is defined by bounded functions; therefore, A is bounded by some M₅, where M₅ = max⁡{M₁, M₃, M₄}.

Suppose the feasible solution of CD4+ cells in the liver lies in the region Θ_c; then,

()

Similarly, assuming the feasible solution of hepatocytes in the liver to lie in the region Θ_h, then

()

Letting M₃ = Q/d₆, it can be deduced that the feasible solution for the model (3)–(10) is

()

2.2.2. The Basic Reproductive Number

When there is no HIV infection in the liver, the system of (3)–(10) settles to a disease-free equilibrium E_d defined by

()

Taking the system of (3)–(10) without medication, that is, ϕ₁ = ϕ₂ = ψ = 0, the basic reproductive number calculated using the next generation method as in [47] is given by

()

where

()

R_0hl is the number of secondary infections in latently infected hepatocytes compartment. R_0ha is the number of secondary infections in productively infected hepatocytes. R_0c is the number of secondary infections produced by one virus producing CD4+ cell. R₀ is the total number of secondary infections in the liver. The total number of secondary infections is directly proportional to the clearance rate of CTLs and inversely proportional to the clearance rate of virions. Generally, R₀ is dependent on antigen-independent CTLs proliferation rate (x) and independent of antigen-dependent proliferation rate (k₃). This indicates that if the CTLs are boosted prior to infection, then the body can handle infection better than when they (CTLs) proliferate in the presence of infection. High CTL clearance rate implies higher numbers of secondary infection. Probably, if many CTLs are cleared from the body by any means, then there are fewer cells left to fight the infection hence faster progression of the infection.

Using Theorem 2 of [47] we establish the following result that the disease-free equilibrium E_d is locally asymptotically stable when R₀ < 1 and unstable when R₀ > 1.

2.2.3. Effective Reproductive Number

Analysing the system of (3)–(10) with the medication (ϕ₁ = ϕ₂ = ψ ≠ 0), we calculated the effective reproductive number (R_e) using the next generation method as in [47]. R_e is the actual average number of secondary cases per primary case that reflects the impact of therapy on infection. Technically, the number of secondary infections during therapy (R_e) should be less than those without therapy (R₀). R_e is defined as

()

where

()

R_ec, R_eha, and R_ehl are defined the same way as R_0c, R_0ha, and R_0hl, respectively, in (25) except that the latter are functions of therapy efficacy and toxicity. Secondary infections in either type of cells largely depend on the drug efficacy. It can be seen that if the drug is 100% effective (ϕ₁ = ϕ₂ = 1), then there would be no secondary infections in either type of cell. However, if the drug is totally ineffective (ϕ₁ = ϕ₂ = 0), it would be expected that the number of secondary infections would be equivalent to those produced when no therapy is administered. This is however not the case, because whether the drug is effective or not, its toxicity will affect the cells involved in drug metabolism.

At present there is no HIV antiretroviral drug that is 100% effective, [48]; likewise, there is no HIV therapy that is free of toxicity [18]. When ϕ₁ = ϕ₂ = 0, it is not straightforward to deduce whether the number of secondary infections in hepatocytes during therapy is less or greater than the number of secondary infections when therapy is not administered. We therefore assess the toxic function that would result in the same number of secondary infections as those when no therapy is administered. We suppose that this is the critical toxic effect ψ_crit of the drug that should not be exceeded if the therapy should reduce the number of secondary infections in the liver. Since toxicity is a function of drug dose, the dose that corresponds to the critical toxic effect can consequently be computed. Using R_0hl + R_0ha = R_ehl + R_eha, the critical toxic effect which is a function of drug efficacy is then calculated and satisfies the equation

()

where

()

It can be shown that a₀ > 0 and a₂ < 0 and in this case we have two possibilities for a positive ψ_crit.

Case 1. When a₁ > 0, that is,

()

then

()

Case 2. When a₁ < 0, that is,

()

then

()

Comparing the two scenarios, we take

and hence deduce the critical drug toxicity that should not be exceeded by HIV medication if it should help in reducing the number of secondary infections, given the appropriate choice of parameters, as

()

2.2.4. Sensitivity Analysis

We carried out sensitivity analysis of the toxic function in the effective reproductive number of the hepatocytes. The study ignored CD4+ cells component of the basic reproductive number in toxic analysis, on assumption that toxic effect of the medication does not have direct effect on CD4+ cells. Following [49], we determined the effect of ψ on R_e first by calculating the difference between R_0h and R_eh as Δ. If Δ > 0 then the toxic effect will slow down the progress of the infection; otherwise it will speed it up:

()

where Λ = (1 − ϕ₂)(NψΦ + s₂(1 − ϕ₂)).

Since 0 ≤ p ≤ 1, the right hand side of (36) is greater than the left hand side provided (NψΦ + s₂(1 − ϕ₂)) < 1. This is not likely because of the values of N and s₂ (100 and 1000, resp.). Therefore Δ < 0; this would imply that R_0h < R_eh, hence indicating that the toxic effect of medication speeds up the progression of infection.

Differentiating R_eh with respect to ψ

()

where

()

From (37), if (AE − FB) > 0 and (pG − d₆C) > 0, that is,

()

then

()

According to [49], in order to slow down the infection rate of the virus when treatment is implemented, the conditions Δ > 0 and ∂R_eh/∂ψ < 0 should be satisfied. Based on the condition derived from (36), the effective reproductive number of hepatocytes is an increasing function of the toxic effect of therapy ψ. This implies that increase in toxicity of medication leads to increase in secondary infections in the liver, provided the relationship between drug efficacies as stated in conditions (39) is fulfilled.

Carrying out sensitivity analysis on the drug efficacies ϕ₁ and ϕ₂, we considered the effective reproductive number R_e of both CD4+ cells and hepatocytes. Starting with reverse transcriptase inhibitors (RTIs),

()

where

()

Since R, Y, Z > 0, then ∂R_e/∂ϕ₁ < 0 indicating that R_e is a decreasing function of RTIs. Thus, increase in efficacy of RTIs implies a reduction in secondary infection.

With protease inhibitors (PIs), we have

()

where

()

It can be shown that ∂R_e/∂ϕ₂ < 0. We can therefore conclude that R_e is a decreasing function of ϕ₁ and ϕ₂ as shown in Figure 1. Increasing the drug efficacy will result in a decrease in secondary infections. Referring to (1), increasing efficacy would necessitate increasing drug dose concentration so that it is much greater than its IC₅₀.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Increase in effective reproductive number with increase in drug efficacy with ψ = 0.5. Horizontal axes represent time in days and parameter values are as shown in Table 2.

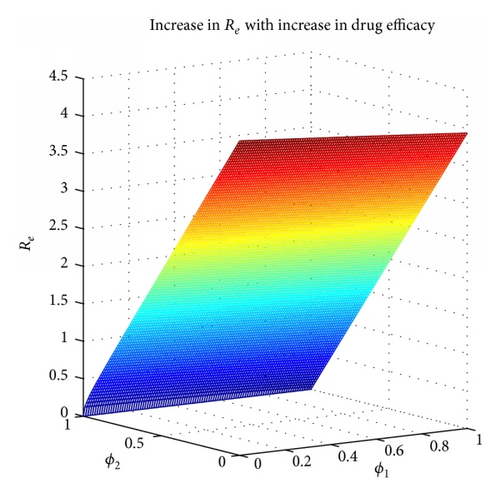
2.2.5. Endemic Equilibrium

Due to the complexity of the model, mathematical analysis is rather cumbersome. We therefore assume a free virus spread of infection and no cell-to-cell transfer of HIV, [50], ruling out the interaction between CD4+ cells and hepatocytes. We therefore split the model into two subpopulations of either cell. We further consider virions produced from either type of cells as the viral production in that subpopulation. We assume a fraction ρ of the total viral population from macrophages to contribute to the viral population in hepatocytes subpopulation while the remainder would contribute to the viral population in CD4+ cells subpopulation. We subdivide the system of (3)–(10) into the following.

CD4+ cells subpopulation infection dynamics:

()

Hepatocytes subpopulation infection dynamics:

()

We derive the endemic equilibrium state as

()

where

()

and

are given by the following equations:

()

in which

()

Differentiating (49) with respect to I_c to obtain the steady states values of I_c, it can be shown that given

()

then there would be two equilibrium values of I_c. Otherwise CD4+ cells would have one positive endemic equilibrium point given by

()

provided the relationship between the two drug efficacies was given by

()

With hepatocytes subpopulation, however, there was no finite number of equilibrium states but rather a rage of values. Therefore, using Descartes rule of signs [51], (50) had at most one positive endemic equilibrium everywhere except in the region θ satisfied by θ = {b₁ < 0, b₂ > 0, b₃ < 0}.

2.2.6. Reduced Model

We reduce the model for further analysis with assumption that RTIs and PIs have an overall drug efficacy given by Φ, where Φ = 1 − (1 − ϕ₁)(1 − ϕ₂) [52]. The combined efficacy Φ reduces the rate at which the virus infects CD4+ cells (β₁) and hepatocytes (β₂). We further assumed that much as macrophages act as reserve source for HIV production throughout HIV infection [53], the level of replication is low as compared to other cells. We therefore revised the model to exclude viral production from macrophages and subdivided it into CD4+ cells and hepatocytes subpopulation. The objective was to investigate the critical combined efficacy of antiretroviral therapy above which the infection would be managed as well as the optimal toxicity below which alanine aminotransferase level in the blood would be negligible.

CD4+ cells subpopulation:

()

Hepatocytes subpopulation:

()

The corresponding endemic equilibrium values for the variables in CD4+ cells subpopulation are

()

in which

()

where

()

It is clear that c₂ > 0 and c₁ > 0. Comparing with (28), (considering 1 − Φ = (1 − ϕ₁)(1 − ϕ₂)) and assuming the effective reproductive number of CD4+ cells to be above unity in HIV infection during therapy, it can be shown that c₀ < 0. Therefore, (58) has one positive root given by

()

To find the critical combined efficacy of antiretroviral therapy, we assume this happens when V⁺ = 0. Since all parameters are nonnegative, then V⁺ can only be zero if

. Thus, the critical efficacy of ART in CD4+ cells above which the infection would be managed would be given by

()

If Φ > Φ_critical then the medication will be able to keep the virus in a controlled state even if the infection remains endemic; that is, the disease-free state and the endemic steady state coexist [54].

In the same way we investigated the optimal toxicity of ART that would not elevate liver enzymes in the blood system even if HIV infection remained endemic. This was assumed to happen when A⁺ = 0; we thus established the endemic equilibrium point in the hepatocyte subpopulation as

()

in which

()

where

()

We previously analysed the critical toxicity that would result in the same level of ALT in the blood as when no therapy is administered and found that this was a function of therapy efficacy. Our aim now is to identify the optimal toxic value ψ_opt of medication that would not lead to elevated alanine aminotransferase in the blood even if HIV remains endemic in the liver. We therefore compute ψ_opt as

()

Like our previous findings, system (65) also shows that the toxicity is a function of efficacy. Analytical solution of ψ_opt from (65) could not be easily obtained since it is also a function of

. We therefore investigated for A⁺ = 0 when

. When

then d₆ψ_opt(d₄ + μ)(d₄ + μ + ψ_opt) = 0. Since (d₄ + μ + ψ_opt) ≠ 0 and (d₄ + μ) ≠ 0 then the only possibility of having no elevated alanine aminotransferase in the blood when HIV is endemic in the liver and the infectious hepatocytes have been reduced to zero is when the medication is not toxic at all. This concurs with various researches that report high levels of liver enzyme in the blood due to toxic nature of all classes of antiretroviral drugs [11, 13–15].

3. Results

3.1. Numerical Simulation

In this section we present the numerical simulations of the model while both the therapeutic and toxic effects of the drugs are incorporated. Medications used in this study are listed in Table 1, while parameter values used in simulations are in Table 2. Parameter values used in calculation of therapeutic and toxic functions in (1) and (2) are shown in Table 1.

Table 2. Parameters used in simulations.

Par.	Description	Value	Source
λ₁	Rate of creation of CD4+ cells from within the body	10 (mL)⁻¹	[36]
d₁	Natural death rate of uninfected CD4+ cells	0.01	[37]
q	Probability that HIV infects hepatocytes	0.2	Estimate
p	Probability that hepatocyte becomes productively infected	0.3	Estimate
μ	Rate at which latently infected hepatocytes become productive	0.006	Estimate
β₁	Rate of transmission of HIV in CD4+ cells	0.00015 (mL)⁻¹	[36]
x	Antigen-independent CTLs proliferation rate	20	[23]
k₁	Rate at which CTLs kill infectious CD4+ cells	50	[38]
k₂	Rate at which CTLs kill infectious hepatocytes	1	[21]
k₃	Antigen-dependent proliferation rate of CTLs	0.2	[39]
d₂	Death rate of infected CD4+ due to infection	0.5	[40]
λ₂	Rate of creation of hepatocytes from within the body	27200	[41]
d₃	Natural death rate of hepatocytes	0.002	[42]
β₂	Rate of transmission of HIV in hepatocytes	0.000015	Estimate
d₄	Death rate of latently infected hepatocytes	0.01	Estimate
d₅	Death rate of infectious hepatocytes	0.5	Estimate
d₆	Rate of clearance of CTLS by all means	0.15	[21]
s₁	Average rate of production of virions by an infected CD4+ cells	50,000	[43]
s₂	Average rate of production of virions by an infected hepatocyte	1000	Estimate
d₇	Death rate of HIV	2	[40]
m	Rate of production of virions from macrophages	5	[23]
N	Virions produced due to drug metabolism	100	Estimate
r	Natural enzyme elevation	14	[44]
d₈	Rate of clearance of ALT from blood system	0.25	[42]
k₄	Rate of generation of liver enzyme in the blood	2000	[42]

Simulating the dynamics of HIV in the liver, three cases were considered: (1) no treatment, (2) with treatment but without toxic effect of the drugs, and (3) with treatment plus toxic effect. Figure 2 depicts the results. Clearly, therapy reduced viral load resulting in fewer number of latent and infectious cells. In case of CD4+ cells, the medication consequently resulted into increased number of uninfected cells. Healthy CD4+ cells were many when the toxic therapy was administered as opposed to when it was not used. However, the dynamics were different in hepatocytes. When the toxic medication was administered, the number of uninfected cells was much less than when medication was not applied at all. This suggested that much as HIV infects hepatocytes, the rate of progression is slower in these types of cells as compared to CD4+ cells [20]. However, hepatocytes seemed to be more affected by toxicity than HIV infection. This was consequently seen in the level of enzymes in the blood that was a lot higher in the case of drug toxicity included than when it was not considered. However, these findings are subject to parameter values and our results are based on parameters in Tables 1 and 2.

The World Health Organisation recommends that antiretroviral therapy be used in combination of NRTIs together with NNRTIs or PIs [55]. This study considered three drugs from NRTIs, one drug from NNRTIs and two drugs from PIs. All combinations from the sample drugs were studied. It is further recommended that atazanavir (ATV) should be used with another PI in a PI-based regimen [55], so it was combined with nelfinavir (NFV). Therapeutic effect of the drugs was modeled using a Hill function as shown in (1). In NNRTI-based regimen, Figure 3 shows that 3TC + DDI + EFV gave the minimal viral load while AZT + d4T + EFV gave the maximal viral load. In PI-based combinations, Figure 4 shows that DDI + 3TC + ATV + NFV gave the least viral load and AZT + d4T + ATV + NFV gave the most. This would suggest that, within the parameter values in Table 2, among the baseline NRTIs studied, DDI + 3TC is the most efficacious and AZT + d4T is the least.

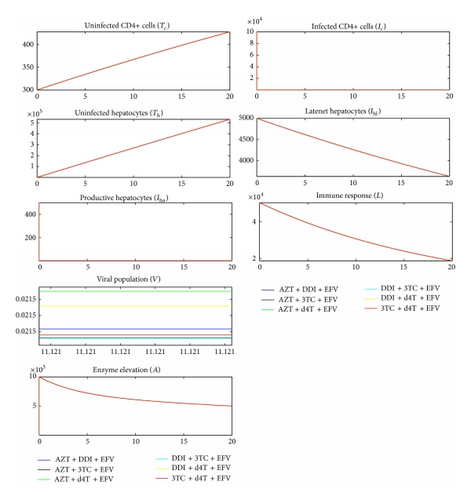
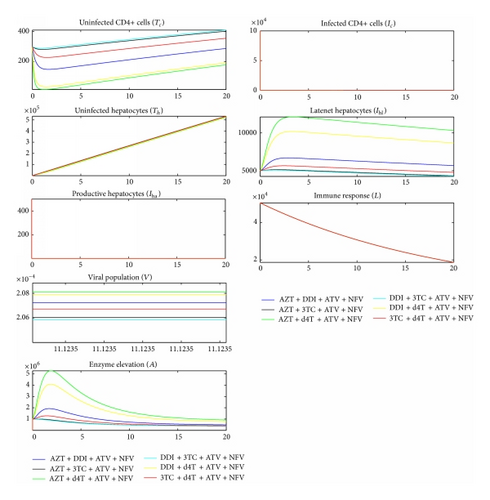
We compared Figures 2, 3, and 4 and established that the level of ALT in the blood when no medication was used was higher than the level of ALT when medication was used. This was contradicting with a number of researches [2–6], indicating that the use of ART increases the level of ALT in the blood stream.

All antiretrovirals are associated with some level of toxicity [5, 56]. During drug metabolism, the toxic nature of ART causes liver cells stress and consequently cell death. This study assumes that the lower the ALT level in the blood the less toxic the therapy. With toxic effect (2) incorporated in the model, simulation results are shown in Figure 5 for NNRTI-based regimen and Figure 6 for PI-based regimen.

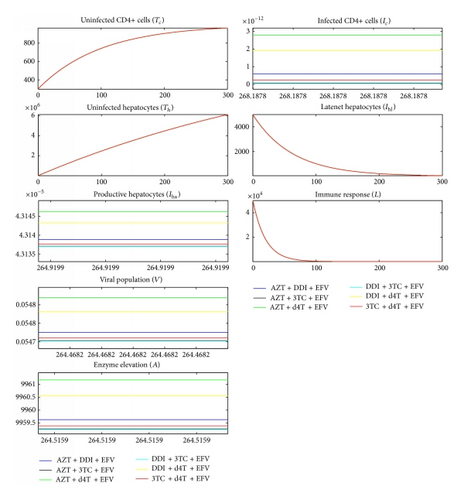
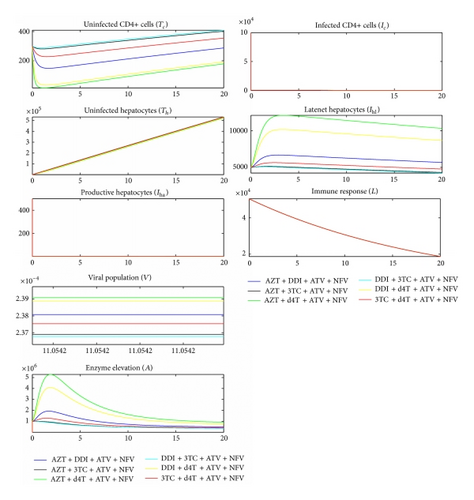
Comparing Figures 5 and 6 and their corresponding dynamics in toxic-free cases in Figures 3 and 4, respectively, it is noted that the level of ALT is highest in the former. It can also be noted that PI-based regimens are more toxic than NNRTI-based regimens among the studied drugs. In NNRT-based regimen, the least toxic combination was 3TC + DDI + EFV while AZT + d4T + EFV was the most toxic. In PI-based regimen, 3TC + DDI + ATV + NFV and AZT + d4T + ATV + NFV were the least and most toxic combinations, respectively. Combinations that contained 3TC were least toxic while combining d4T with either AZT or DDI made the combination toxic. This is consistent with a number of researches that assert that 3TC is the least toxic NRTI while d4T is the most toxic [18, 25, 48, 55, 57].

4. Discussion

Much as liver injury can occur solely due to HIV infection [7–10], liver related mortality and morbidity are being associated with the use of antiretroviral therapy, [2–6], because all antiretroviral therapy has some degree of toxicity, [15]. This study used a mathematical model with therapy efficacy as well as toxicity incorporated, to study various types of HIV drugs.

The study investigated for toxicity threshold between 0 and 1 inclusive, below which HIV infection in the liver can be controlled. Mathematical analysis showed that the critical toxicity threshold was a function of drug efficacy. The dependency of toxicity on efficacy would be due to the fact that both are dose-dependent [26, 28].

With parameter values as given in Table 2, without including the toxic effect of medication, in NNRTI-based regimen, the combination of DDI + 3TC that contained EFV gave the minimal viral load while the combination of AZT + d4T gave the maximum. In PI-based regimen, the combination of ATV + NFV + DDI + 3TC gave the least viral load while ATV + NFV + AZT + d4T gave the highest.

With toxicity incorporated and parameter values as in Table 2, in NNRTIs-based combinations, DDI + EFV + 3TC produced the minimal level of ALT, while including d4T + EFV + AZT gave maximal ALT level in the blood system. In PI-based regimen the most toxic combination was d4T + ATV + NFV + AZT while the least toxic was DDI + ATV + NFV + 3TC. Our findings are consistent with [24, 58], who recommend that d4T should not be combined with AZT because the combination is highly toxic. PI-based regimens were found to be the most toxic and at the same time the best in reducing viral load in the liver as compared to NNRTI-based regimens [24, 25, 58].

5. Conclusion

The findings regarding toxic and therapeutic effects of NRTI drugs were consistent with the already existing literature. We therefore deduce that, with the drugs studied and parameter values used, the most toxic combination gave the highest viral load in the liver and vice versa. It is important to note that there was no variability in NNRTIs and PIs as a single drug from NNRTIs and same combination from PIs was used. The same method could possibly be used with various drugs in NNRI-based and PI-based regimens to explore the most therapeutic and toxic combinations in HIV therapy.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

The authors would like to acknowledge the Sida/SAREC bilateral research cooperation programme of Makerere University for funding this research. They also would like to thank the Center for International Mobility (CIMO), Finland, for funding research visits to Lappeenranta University of Technology.

References

1 Babu C., Suwansrinon K., Bren G., Badley A., and Rizza S., HIV induces TRAIL sensitivity in hepatocytes, PLoS ONE. (2009) 4, no. 2, e4623, https://doi.org/10.1371/journal.pone.0004623.
Google Scholar
2 McKoy J., Bennett C., Scheetz M. et al., Hepatotoxicity associated with long-versus short-course HIV prophylactic nevirapine use: a systematic review and meta-analysis from the research on adverse drug events and reports (RADAR) project, Journal of Viral Hepatitis. (2009) 32, no. 2, 147–158.
Google Scholar
3 Gisolf E. H., Dreezen C., Danner S. A., Weel J. L. F., and Weverling G. J., Risk factors for hepatotoxicity in HIV-1-infected patients receiving ritonavir and saquinavir with or without stavudine, Clinical Infectious Diseases. (2000) 31, no. 5, 1234–1239, https://doi.org/10.1086/317449, 2-s2.0-0034457420.
Google Scholar
4 Iser D. and Lewin S., The pathogenesis of liver disease in the setting of HIV-hepatitis B virus coinfection, Antiviral Therapy. (2009) 14, no. 2, 155–164, 2-s2.0-67149113908.
Google Scholar
5 Jain M. K., Opio C. K., Osuagwu C. C., Pillai R., Keiser P., and Lee W. M., Do HIV care providers appropriately manage hepatitis B in coinfected patients treated with antiretroviral therapy?, Clinical Infectious Diseases. (2007) 44, no. 7, 996–1000, https://doi.org/10.1086/512367, 2-s2.0-33947415368.
Google Scholar
6 Landrum M. L., Fieberg A. M., Chun H. M., Crum-Cianflone N. F., Marconi V. C., Weintrob A. C., Ganesan A., Barthel R. V., Wortmann G., and Agan B. K., The effect of human immunodeficiency virus on hepatitis B virus serologic status in co-infected adults, PLoS ONE. (2010) 5, no. 1, e8687, https://doi.org/10.1371/journal.pone.0008687, 2-s2.0-77952472602.
Google Scholar
7 Nampala H., Luboobi L. S., Mugisha J. Y., and Obua C., Mathematical modeling of liver enzyme elevation in HIV mono-infection, Mathematical Biosciences. (2013) 242, no. 1, 77–85, https://doi.org/10.1016/j.mbs.2012.12.005, MR3033471, 2-s2.0-84873255122.
CAS PubMed Web of Science® Google Scholar
8 Xiao P., Usami O., Suzuki Y., Ling H., Shimizu N., Hoshino H., Zhuang M., Ashino Y., Gu H., and Hattori T., Characterization of a CD4-independent clinical HIV-1 that can efficiently infect human hepatocytes through chemokine (C-X-C motif) receptor 4, AIDS. (2008) 22, no. 14, 1749–1757, https://doi.org/10.1097/QAD.0b013e328308937c, 2-s2.0-66349116273.
Google Scholar
9 Blackard J. T. and Sherman K. E., HCV/HIV co-infection: time to re-evaluate the role of HIV in the liver?, Journal of Viral Hepatitis. (2008) 15, no. 5, 323–330, https://doi.org/10.1111/j.1365-2893.2008.00970.x, 2-s2.0-41549090888.
Google Scholar
10 Crane M., Visvanathan K., and Lewin S. R., HIV infection and TLR signalling in the liver, Gastroenterology Research and Practice. (2012) 2012, 8, 473925, https://doi.org/10.1155/2012/473925, 2-s2.0-84858304160.
10.1155/2012/473925
Google Scholar
11 Balagopal A., Ray S. C., de Oca R. M., Sutcliffe C. G., Vivekanandan P., Higgins Y., Mehta S. H., Moore R. D., Sulkowski M. S., Thomas D. L., and Torbenson M. S., Kupffer cells are depleted with HIV immunodeficiency and partially recovered with antiretroviral immune reconstitution, AIDS. (2009) 23, no. 18, 2397–2404, https://doi.org/10.1097/QAD.0b013e3283324344, 2-s2.0-72949120591.
Google Scholar
12 Liddle C. and Stedman C., Hepatic Metabolism of Drugs, 2007, Wiley-Blackwell.
Google Scholar
13 Hewitt N. J., Lechón M. J. G., Houston J. B., Hallifax D., Brown H. S., Maurel P., Kenna J. G., Gustavsson L., Lohmann C., Skonberg C., Guillouzo A., Tuschl G., Li A. P., Lecluyse E., Groothuis G. M. M., and Hengstler J. G., Primary hepatocytes: current understanding of the regulation of metabolic enzymes and transporter proteins, and pharmaceutical practice for the use of hepatocytes in metabolism, enzyme induction, transporter, clearance, and hepatotoxicity studies, Drug Metabolism Reviews. (2007) 39, no. 1, 159–234, https://doi.org/10.1080/03602530601093489, 2-s2.0-33847018050.
Google Scholar
14 Malhi H., Guicciardi M. E., and Gores G. J., Hepatocyte death: a clear and present danger, Physiological Reviews. (2010) 90, no. 3, 1165–1194, https://doi.org/10.1152/physrev.00061.2009, 2-s2.0-77955591462.
Web of Science® Google Scholar
15 Griffin L., Interactions of antiretroviral protease inhibitors with hepatic transport proteins: mechanisms of drug-induced liver injury [Ph.D. thesis], 2012, University of North Carolina at Chapel Hill, Chapel Hill, NC, USA.
Google Scholar
16 Cao Y., Friedman-Kien A. E., Huang Y., Li X. L., Mirabile M., Moudgil T., Zucker-Franklin D., and Ho D. D., CD4-independent, productive human immunodeficiency virus type 1 infection of hepatoma cell lines in vitro, Journal of Virology. (1990) 64, no. 6, 2553–2559, 2-s2.0-0025295298.
Google Scholar
17 Vlahakis S. R., Villasis-Keever A., Gomez T. S., Bren G. D., and Paya C. V., Human immunodeficiency virus-induced apoptosis of human hepatocytes via CXCR4, Journal of Infectious Diseases. (2003) 188, no. 10, 1455–1460, https://doi.org/10.1086/379738, 2-s2.0-0346874146.
Google Scholar
18 Núñez M., Clinical syndromes and consequences of antiretroviral-related hepatotoxicity, Hepatology. (2010) 52, no. 3, 1143–1155, https://doi.org/10.1002/hep.23716, 2-s2.0-77956624153.
Google Scholar
19 Crane M., Iser D., and Lewin S., Human immunodeficiency virus infection and the liver, World Journal of Hepatology. (2012) 4, no. 3, 91–98, https://doi.org/10.4254/wjh.v4.i3.91, 2-s2.0-84883802447.
Google Scholar
20 Kong L., Maya W. C., Moreno-Fernandez M. E., Ma G., Shata M. T., Sherman K. E., Chougnet C., and Blackard J. T., Low-level HIV infection of hepatocytes, Virology Journal. (2012) 9, article 157, https://doi.org/10.1186/1743-422X-9-157, 2-s2.0-84864700529.
Google Scholar
21 Arnaout R. A., Nowak M. A., and Wodarz D., HIV-1 dynamics revisited: biphasic decay by cytotoxic T lymphocyte killing?, Proceedings of the Royal Society B: Biological Sciences. (2000) 267, no. 1450, 1347–1354, https://doi.org/10.1098/rspb.2000.1149, 2-s2.0-0034617009.
Google Scholar
22 Rong L., Gilchrist M. A., Feng Z., and Perelson A. S., Modeling within-host {HIV}-1 dynamics and the evolution of drug resistance: trade-offs between viral enzyme function and drug susceptibility, Journal of Theoretical Biology. (2007) 247, no. 4, 804–818, https://doi.org/10.1016/j.jtbi.2007.04.014, MR2479625, 2-s2.0-34447528803.
Google Scholar
23 Gumel A. B., Zhang X.-W., Shivakumar P. N., Garba M. L., and Sahai B. M., A new mathematical model for assessing therapeutic strategies for HIV infection, Journal of Theoretical Medicine. (2002) 4, no. 2, 147–155, https://doi.org/10.1080/1027366021000003289, ZBL1054.92031, 2-s2.0-0036319885.
10.1080/1027366021000003289
Google Scholar
24 AIDSinfo, Side effects of anti-hiv medications, health information for patients, U.S. Department of Health and Human Services, http://aidsinfo.nih.gov/contentfiles/sideeffectanithivmeds_cbrochure_en.pdf.
Google Scholar
25 Sharma B., Anti-HIV-1 drug toxicity and management strategies, Neurobehavioral HIV Medicine. (2011) 3, no. 1, 27–40, https://doi.org/10.2147/NBHIV.S11748, 2-s2.0-80053061298.
Google Scholar
26 Perelson A. S. and Deeks S. G., Drug effectiveness explained: the mathematics of antiviral agents for HIV, Science Translational Medicine. (2011) 3, no. 91, 91ps30, https://doi.org/10.1126/scitranslmed.3002656, 2-s2.0-79960371691.
Google Scholar
27 Lin W., Wu G., Li S., Weinberg E. M., Kumthip K., Peng L. F., Méndez-Navarro J., Chen W.-C., Jilg N., Zhao H., Goto K., Zhang L., Brockman M. A., Schuppan D., and Chung R. T., HIV and HCV cooperatively promote hepatic fibrogenesis via induction of reactive oxygen species and NF κB, The Journal of Biological Chemistry. (2011) 286, no. 4, 2665–2674, https://doi.org/10.1074/jbc.M110.168286, 2-s2.0-78951476859.
Google Scholar
28 Shen L., Rabi S. A., Sedaghat A. R., Shan L., Lai J., Xing S., and Siliciano R. F., A critical subset model provides a conceptual basis for the high antiviral activity of major HIV drugs, Science Translational Medicine. (2011) 3, no. 91, 91ra63, https://doi.org/10.1126/scitranslmed.3002304, 2-s2.0-79960373686.
Google Scholar
29 Krakovska O. and Wahl L. M., Optimal drug treatment regimens for HIV depend on adherence, Journal of Theoretical Biology. (2007) 246, no. 3, 499–509, https://doi.org/10.1016/j.jtbi.2006.12.038, MR2306882, 2-s2.0-34247630656.
CAS PubMed Web of Science® Google Scholar
30 Shen L., Peterson S., Sedaghat A. R., McMahon M. A., Callender M., Zhang H., Zhou Y., Pitt E., Anderson K. S., Acosta E. P., and Siliciano R. F., Dose-response curve slope sets class-specific limits on inhibitory potential of anti-HIV drugs, Nature Medicine. (2008) 14, no. 7, 762–766, https://doi.org/10.1038/nm1777, 2-s2.0-46049096485.
Google Scholar
31 van der Lugt J. and Avihingsanon A., Clinical pharmacology and pharmacokinetics of antiretrovirals in Asia, Asian Biomedicine. (2009) 3, no. 1, 53–62, 2-s2.0-70349335882.
Google Scholar
32 Bristol-Myers, The electronic Medicines Compendium (eMC), Bristol-Myers Squibb Pharmaceutical Limited, http://www.medicines.org.uk/emc/medicine/21122.
Google Scholar
33 Bisset L. R., Lutz H., Böni J., Hofmann-Lehmann R., Lüthy R., and Schüpbach J., Combined effect of zidovudine (ZDV), lamivudine (3TC) and abacavir (ABC) antiretroviral therapy in suppressing in vitro FIV replication, Antiviral Research. (2002) 53, no. 1, 35–45, https://doi.org/10.1016/S0166-3542(01)00190-5, 2-s2.0-0036027833.
Google Scholar
34 Bristol-Myers Squibb & Gilead Sciences, Sciences, Product monograph: Atripla (efavirenz/emtricitabine/tenofov ir disoproxil fumarate tablets) 600 mg/200 mg/300 mg antiretroviral agent, http://www.gilead.ca/.
Google Scholar
35 AIDSinfo, Aidsinfo drug database, http://aidsinfo.nih.gov/guidelines/html/3/perinatal-guidelines/213/nel_navir-viracept-nfv.
Google Scholar
36 Nowak M. A., Bonhoeffer S., Shaw G. M., and May R. M., Anti-viral drug treatment: dynamics of resistance in free virus and infected cell populations, Journal of Theoretical Biology. (1997) 184, no. 2, 203–217, https://doi.org/10.1006/jtbi.1996.0307, 2-s2.0-0031581661.
Google Scholar
37 Srivastava P. and Chandara P., Modeling the dynamics of HIV and CD4⁺ T cells during primary infection, Nonlinear Analysis: Real World Applications. (2008) 11, no. 2, 612–618, https://doi.org/10.1016/j.nonrwa.2008.10.037.
Google Scholar
38 Smith R. J. and Schwartz E. J., Predicting the potential impact of a cytotoxic T-lymphocyte HIV vaccine: how often should you vaccinate and how strong should the vaccine be?, Mathematical Biosciences. (2008) 212, no. 2, 180–187, https://doi.org/10.1016/j.mbs.2008.02.001, MR2401338, 2-s2.0-40949109686.
Google Scholar
39 Rong L. and Perelson A. S., Modeling latently infected cell activation: viral and latent reservoir persistence, and viral blips in HIV-infected patients on potent therapy, PLoS Computational Biology. (2009) 5, no. 10, 18, e1000533, https://doi.org/10.1371/journal.pcbi.1000533, MR2575020, 2-s2.0-73449117263.
Google Scholar
40 Wodarz D. and Nowak M., Immune responses and viral phenotype: do replication rate and cytopathogenicity inuence virus load?, Journal of Theorerical Medicine. (1999) 2, 113–127.
Google Scholar
41 Ciupe S. M., Ribeiro R. M., Nelson P. W., and Perelson A. S., Modeling the mechanisms of acute hepatitis B virus infection, Journal of Theoretical Biology. (2007) 247, no. 1, 23–35, https://doi.org/10.1016/j.jtbi.2007.02.017, MR2306969, 2-s2.0-34248677854.
Web of Science® Google Scholar
42 Long C., Qi H., and Huang S.-H., Mathematical modeling of cytotoxic lymphocyte-mediated immune response to hepatitis B virus infection, Journal of Biomedicine and Biotechnology. (2008) 2008, 9, 743690, https://doi.org/10.1155/2008/743690, 2-s2.0-41149090134.
10.1155/2008/743690
PubMed Google Scholar
43 De Boer R. J., Ribeiro R. M., and Perelson A. S., Current estimates for HIV-1 production imply rapid viral clearance in lymphoid tissues, PLoS Computational Biology. (2010) 6, no. 9, e1000906, https://doi.org/10.1371/journal.pcbi.1000906, MR2741163, 2-s2.0-78049444596.
Google Scholar
44 Su Y., Wen Y., and Min L., Analysis of a HBV infection model with ALT, Proceedings of the IEEE 6th International Conference on Systems Biology, August 2012, Xi′an, China, 97–100, https://doi.org/10.1109/ISB.2012.6314119, 2-s2.0-84868671707.
Google Scholar
45 Elsady Z. A., On the solution of an HIV-immune dynamic system, International Journal of Physical Sciences. (2008) 3, no. 1, 12–17, 2-s2.0-70350087618.
Google Scholar
46 King R. W., Klabe R. M., Reid C. D., and Erickson-Viitanen S. K., Potency of nonnucleoside reverse transcriptase inhibitors (NNRTIs) used in combination with other human immunodeficiency virus NNRTIs, NRTIs, or protease inhibitors, Antimicrobial Agents and Chemotherapy. (2002) 46, no. 6, 1640–1646, https://doi.org/10.1128/AAC.46.6.1640-1646.2002, 2-s2.0-0036090544.
Google Scholar
47 van den Driessche P. and Watmough J., Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission, Mathematical Biosciences. (2002) 180, 29–48, https://doi.org/10.1016/S0025-5564(02)00108-6, MR1950747, ZBL1015.92036, 2-s2.0-0036845274.
10.1016/S0025-5564(02)00108-6
Web of Science® Google Scholar
48 Campbell T. B., Smeaton L. M., Kumarasamy N., Flanigan T., Klingman K. L., Firnhaber C., Grinsztejn B., Hosseinipour M. C., Kumwenda J., Lalloo U., Riviere C., Sanchez J., Melo M., Supparatpinyo K., Tripathy S., Martinez A. I., Nair A., Walawander A., Moran L., Chen Y., Snowden W., Rooney J. F., Uy J., Schooley R. T., de Gruttola V., Hakim J. G., Swann E., Barnett R. L., Brizz B., Delph Y., Gettinger N., Mitsuyasu R. T., Eshleman S., Safren S., Fiscus S. A., Andrade A., Haas D. W., Amod F., Berthaud V., Bollinger R. C., Bryson Y., Celentano D., Chilongozi D., Cohen M., Collier A. C., Currier J. S., Cu-Uvin S., Eron J., Flexner C., Gallant J. E., Gulick R. M., Hammer S. M., Hoffman I., Kazembe P., Kumwenda N., Lama J. R., Lawrence J., Maponga C., Martinson F., Mayer K., Nielsen K., Pendame R. B., Ramratnam B., Sanne I., Severe P., Sirisanthana T., Solomon S., Tabet S., Taha T., van der Horst C., Wanke C., Gormley J., Marcus C. J., Putnam B., Ntshele S., Loeliger E., Pappa K. A., Webb N., Shugarts D. L., Winters M. A., Descallar R. S., Steele J., Wulfsohn M., Said F., Martin J. C., Bischofberger N., Cheng A., Jaffe H., Sharma J., Poongulali S., Cardoso S. W., Faria D. L., Berendes S., Burke K., Mngqibisa R., Kanyama C., Kayoyo V., Samaneka W. P., Chisada A., Faesen S., Chariyalertsak S., Santos B., Lira R. A., Joglekar A. A., la Rosa A., Infante R., Jain M., Petersen T., Godbole S., Dhayarkar S., Feinberg J., Baer J., Pollard R. B., Asmuth D., Gangakhedkar R. R., Gaikwad A., Ray M. G., Basler C., Para M. F., Watson K. J., Taiwo B., McGregor D., Balfour H. H., Mullan B., Kim G.-Y., Klebert M. K., Cox G. M., Silberman M., Mildvan D., Revuelta M., Tashima K. T., Patterson H., Geiseler P. J., Daar E. S., Lopez R., Frarey L., Currin D., Haas D. H., Bailey V. L., Tebas P., Zifchak L., Noel-Connor J., Torres M., Sha B. E., Fritsche J. M., Cespedes M., Forcht J., O′Brien W. A., Mogridge C., Hurley C., Corales R., Palmer M., Adams M., Luque A., Lopez-Detres L., and Stroberg T., Efficacy and safety of three antiretroviral regimen s for initial treatment of hiv- 1: a randomized clinical trial in diverse multinational settings, PLoS Medicine. (2012) 9, no. 8, e1001290, https://doi.org/10.1371/journal.pmed.1001290, 2-s2.0-84865566725.
Google Scholar
49 Hsu Schmitz S.-F., Effects of treatment or/and vaccination on HIV transmission in homosexuals with genetic heterogeneity, Mathematical Biosciences. (2000) 167, no. 1, 1–18, https://doi.org/10.1016/S0025-5564(00)00021-3, ZBL0979.92023, 2-s2.0-0033845033.
Google Scholar
50 Culshaw R. V., Ruan S., and Webb G., A mathematical model of cell-to-cell spread of HIV-1 that includes a time delay, Journal of Mathematical Biology. (2003) 46, no. 5, 425–444, https://doi.org/10.1007/s00285-002-0191-5, MR1998996, 2-s2.0-1642380503.
Google Scholar
51 Anderson B., Jackson J., and Sitharam M., Descartes′ rule of signs revisited, The American Mathematical Monthly. (1998) 105, no. 5, 447–451, https://doi.org/10.2307/3109807, MR1622513, ZBL0913.12001, 2-s2.0-0032386231.
Google Scholar
52 Rong L. and Perelson A. S., Asymmetric division of activated latently infected cells may explain the decay kinetics of the HIV-1 latent reservoir and intermittent viral blips, Mathematical Biosciences. (2009) 217, no. 1, 77–87, https://doi.org/10.1016/j.mbs.2008.10.006, MR2489340, 2-s2.0-57749177930.
Web of Science® Google Scholar
53 Nasr N., Maddocks S., Turville S. G., Harman A. N., Woolger N., Helbig K. J., Wilkinson J., Bye C. R., Wright T. K., Rambukwelle D., Donaghy H., Beard M. R., and Cunningham A. L., HIV-1 infection of human macrophages directly induces viperin which inhibits viral production, Blood. (2012) 120, no. 4, 778–788, https://doi.org/10.1182/blood-2012-01-407395, 2-s2.0-84864491073.
Google Scholar
54 Callaway D. S. and Perelson A. S., HIV-1 infection and low steady state viral loads, Bulletin of Mathematical Biology. (2002) 64, no. 1, 29–64, https://doi.org/10.1006/bulm.2001.0266, 2-s2.0-0036381110.
Web of Science® Google Scholar
55 AIDSinfo, Guidelines for the use of antiretroviral agents in hiv-1-infected adults and adolescents, Department of Health and Human Services, http://aidsinfo.nih.gov/ContentFiles/AdultandAdolescentGL.pdf.
Google Scholar
56 Powderly W., Antiretroviral therapy in patients with hepatitis and HIV: weighing risks and benefits, Clinical Infectious Diseases. (2004) 38, no. supplement 2, S109–S113, https://doi.org/10.1086/381443, 2-s2.0-1542297620.
Google Scholar
57 Fisher M., Hepatotoxicity of antiretroviral therapy, Proceedings of the International Conference on Viral Hepatitis, March 2013, New York, NY, USA.
Google Scholar
58 Montessori V., Press N., Harris M., Akagi L., and Montaner J., Adverse e ff ects of antiretroviral therapy for hiv infection, Canadian Medical Association or Its Licensors. (2004) 170, no. 2, 229–238.
Google Scholar

Citing Literature

All articles

Modelling Hepatotoxicity of Antiretroviral Therapy in the Liver during HIV Monoinfection

Abstract

1. Introduction

2. Material and Methods

2.1. Mathematical Model Development

2.2. Model Analysis

2.2.1. Positivity and Boundedness of Solutions

2.2.2. The Basic Reproductive Number

2.2.3. Effective Reproductive Number

2.2.4. Sensitivity Analysis

2.2.5. Endemic Equilibrium

2.2.6. Reduced Model

3. Results

3.1. Numerical Simulation

4. Discussion

5. Conclusion

Conflict of Interests

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Modelling Hepatotoxicity of Antiretroviral Therapy in the Liver during HIV Monoinfection

Abstract

1. Introduction

2. Material and Methods

2.1. Mathematical Model Development

2.2. Model Analysis

2.2.1. Positivity and Boundedness of Solutions

2.2.2. The Basic Reproductive Number

2.2.3. Effective Reproductive Number

2.2.4. Sensitivity Analysis

2.2.5. Endemic Equilibrium

2.2.6. Reduced Model

3. Results

3.1. Numerical Simulation

4. Discussion

5. Conclusion

Conflict of Interests

Acknowledgments

References

Citing Literature

Figures

References

Related

Information