Volume 2014, Issue 1 653065

Research Article

Open Access

Planar and Nonplanar Solitary Waves in a Four-Component Relativistic Degenerate Dense Plasma

M. R. Hossen,

Corresponding Author

M. R. Hossen

[email protected]

Department of Physics, Jahangirnagar University, Savar, Dhaka 1342, Bangladesh juniv.edu

Search for more papers by this author

L. Nahar,

L. Nahar

Department of Physics, Jahangirnagar University, Savar, Dhaka 1342, Bangladesh juniv.edu

Search for more papers by this author

A. A. Mamun,

A. A. Mamun

Department of Physics, Jahangirnagar University, Savar, Dhaka 1342, Bangladesh juniv.edu

Search for more papers by this author

M. R. Hossen,

Corresponding Author

M. R. Hossen

[email protected]

Department of Physics, Jahangirnagar University, Savar, Dhaka 1342, Bangladesh juniv.edu

Search for more papers by this author

L. Nahar,

L. Nahar

Department of Physics, Jahangirnagar University, Savar, Dhaka 1342, Bangladesh juniv.edu

Search for more papers by this author

A. A. Mamun,

A. A. Mamun

Department of Physics, Jahangirnagar University, Savar, Dhaka 1342, Bangladesh juniv.edu

Search for more papers by this author

First published: 23 October 2014

https://doi.org/10.1155/2014/653065

Citations: 20

Academic Editor: Milan S. Dimitrijevic

Share a link

Email
Wechat
Bluesky

Abstract

The nonlinear propagation of electrostatic perturbation modes in an unmagnetized, collisionless, relativistic, degenerate plasma (containing both nonrelativistic and ultrarelativistic degenerate electrons, nonrelativistic degenerate ions, and arbitrarily charged static heavy ions) has been investigated theoretically. The Korteweg-de Vries (K-dV) equation has been derived by employing the reductive perturbation method. Their solitary wave solution is obtained and numerically analyzed in case of both planar and nonplanar (cylindrical and spherical) geometry. It has been observed that the ion-acoustic (IA) and modified ion-acoustic (mIA) solitary waves have been significantly changed due to the effects of degenerate plasma pressure and number densities of the arbitrarily charged heavy ions. It has been also found that properties of planar K-dV solitons are quite different from those of nonplanar K-dV solitons. There are numerous variations in case of mIA solitary waves due to the polarity of heavy ions. The basic features and the underlying physics of IA and mIA solitary waves, which are relevant to some astrophysical compact objects, are briefly discussed.

1. Introduction

A large fraction of matter in the universe is in the plasma state. Significant attention has been devoted to the study of ion-acoustic (IA) waves in plasmas not only from an academic point of view, but also from the view of its vital role in understanding the nonlinear features of localized electrostatic disturbances in laboratory and space environments [1–6]. The basic features of solitary waves associated with IA waves, in which electron thermal pressure gives rise to a restoring force and ion mass provides the inertia, were first theoretically predicted by Washimi and Tanuiti by assuming an ideal plasma containing cold ions and isothermal electrons. These basic features [7] were verified by a novel laboratory experiment of Ikezi et al. [6].

Presently, relativistic degeneracy of plasmas has received great attention because of its vital role in different astrophysical environments [8, 9], where particle velocities become comparable to the speed of light. Astrophysical compact objects such as white dwarfs, neutron stars, quasars, black holes, and pulsars are examples where relativistic degenerate plasmas are dominant and interesting new phenomena are investigated by several nonlinear effects in such plasmas. The basic constituents of white dwarfs are mainly oxygen, carbon, and helium with an envelope of hydrogen gas. In some relatively massive white dwarfs, one can think of the presence of heavier element like iron within the stars. The existence of heavy elements is found to form in a prestellar stage of the evolution of the universe, when all matter was compressed to extremely high densities and possessed correspondingly high temperatures [10]. In case of such a compact object the degenerate electron number density is so high (in white dwarfs it can be of the order of 10³⁰ cm⁻³, even more [8]).

Chandrasekhar [11, 12] presented a general expression for the relativistic ion and electron pressures in his classical papers. The pressure for ion fluid can be given by the following equation:

()

where

()

for the nonrelativistic limit (where Λ_c = πħ/mc = 1.2 × 10⁻¹⁰ cm and ħ is the Planck constant divided by 2π), while for the electron fluid,

()

where

()

in the ultrarelativistic limit [11–14].

We note that we have considered both electron and ion degeneracy, but light electrons are assumed to be relativistic (nonrelativistic and ultrarelativistic) and ions (which are heavier than electrons) are assumed to be nonrelativistic. Equations (1) and (3) represent the equations of state of ion and electron pressure in high density regime.

Recently, several authors have used the pressure laws to observe the linear and nonlinear properties of electrostatic [15–19] and electromagnetic [20, 21] waves by using only nonrelativistic or both nonrelativistic and ultrarelativistic quantum hydrodynamics (QHD) [22] and quantum-magnetohydrodynamics (QMHD) models [23, 24]. The solution of the Dirac equation for electrostatic and electromagnetic waves in a relativistic quantum plasmas has been discussed by Mendonca and Serbeto [25]. Masood and Eliasson considered an unmagnetized quantum plasma with relativistically degenerate electrons and cold fluid ions and they studied the basic features of the solitary structures [26]. Later on, Shukla et al. [27] theoretically investigated the nonlinear propagation of electrostatic waves in degenerate quantum plasma. They considered strongly coupled nondegenerate ions and degenerate electron fluids in an unmagnetized dense plasma and studied the basic properties of solitary and shock structures. Zeba et al. [28] considered a warm collisionless electron-positron-ion plasma with ultrarelativistic degenerate electrons and positrons and investigated theoretically the existence regions for ion solitary pulses. Since the dense astrophysical quantum plasmas can be confined by stationary heavy ions, therefore the effect of the heavy ions has to be taken into account, especially for astrophysical observations (such as white dwarfs, neutron stars, and black holes) where the degenerate plasma pressure and heavy ions play an important role in the formation and stability of the existing waves. Recently, Zobaer et al. [9, 15, 16, 29] also considered nonrelativistic ion fluids and both nonrelativistic and ultrarelativistic electron fluids and theoretically investigated the basic features of solitary, shock, and double layer structures. All of these investigations are mainly based on planar geometry and they did not consider the effect of heavy ions, which may not be a realistic situation in space environments. Since the waves observed in astrophysical compact objects are certainly not infinite in one dimension (1D) and there is a great possibility of having both positively and negatively charged heavy ions, there are several cases of practical importance where planar geometry does not work and one would have to consider a nonplanar geometry. The notable examples where nonplanar geometry plays a vital role are white dwarfs, neutron stars, black holes, circumstellar disks, dark molecular clouds, cometary tails, and so forth. Till now, no theoretical investigation has been made to study the extreme conditions of matter for both nonrelativistic and ultrarelativistic limits and arbitrarily (both positively and negatively) charged heavy ions on a planar and nonplanar (cylindrical and spherical) geometry. Therefore, in our present work, we attempt to study the basic features of planar and nonplanar IA and mIA solitary waves by deriving the Korteweg-de Vries equation in a dense plasma containing degenerate electron and ion fluids and arbitrarily charged static heavy ions.

The paper is organized as follows. The governing equations are provided in Section 2. The K-dV equation is derived in Section 3. The profiles of K-dV solitons are presented in Section 4 and numerically analyzed in order. Finally, a brief discussion is given in Section 5.

2. Governing Equations

We consider a nonplanar (cylindrical and spherical) geometry and nonlinear propagation of mIA waves (consisting of arbitrarily charged static heavy ions, nonrelativistic degenerate cold ions, and both nonrelativistic and ultrarelativistic degenerate electron fluids) in an unmagnetized, collisionless dense plasma. Hence, at equilibrium, we have Z_in_i0 + jZ_hn_h0 = n_e0, where n_s0 is the particle number density of the species s with s = e(i)h for electrons (ions) heavy ions, Z_h is the number of ions residing onto the heavy ion surface, and e is the magnitude of charge of an electron and j = +1(j = −1) for positively (negatively) charged heavy ions. The nonlinear dynamics of the electrostatic waves propagating in such a degenerate dense plasma system is governed by the following normalized equations:

()

where ν = 0 for one-dimensional planar geometry and ν = 1(2) for nonplanar cylindrical (spherical) geometry; n_i (n_e) is the ion (electron) number densities normalized by its equilibrium value n_i0 (n_e0), u_i is the ion fluid speed normalized by C_i = (m_ec²/m_i) ^1/2 with m_e (m_i) being the electron (ion) rest mass, c is the speed of light in vacuum, and ϕ is the electrostatic wave potential normalized by m_ec²/e with e being the magnitude of the charge of an electron. Here μ( = Z_hn_h0/Z_pn_i0) is the ratio of the number density of heavy ions and positive ions multiplied by their charge per ion (Z_h/Z_p). When μ = 0 the situation acts as normal electron-ion plasma system. The polarity of the heavy ions depends on the parameter j. When j = +1(−1) the heavy ions act as positively (negatively) charged in this plasma system. The time variable (t) is normalized by ω_pi = (4πn₀e²/m_i) ^1/2, and the space variable (r) is normalized by λ_s = (m_ec²/4πn₀e²) ^1/2. The relativistic constants are

, and

3. Derivation of K-dV Equation

Now we derive the K-dV equation by employing the reductive perturbation technique to examine the electrostatic perturbations propagating in this dense plasma system and introduce the stretched coordinates [30] as follows:

()

where V_p is the wave phase speed (ω/k with ω being the angular frequency and k being the wave number of the perturbation mode) and ϵ is a smallness parameter measuring the weakness of the dispersion (0 < ϵ < 1). We then expand the parameters n_i, n_e, u_i, ϕ, and ρ in power series of ϵ:

()

Now, expressing (5) (using (6)) in terms of ξ and τ and substituting (7) into (5), one can easily develop different sets of equations in various powers of ϵ. To the lowest order in ϵ, we have , , , and , where and . The relation represents the dispersion relation as well as the phase velocity for the mIA-type electrostatic waves in this degenerate plasma under consideration.

To the next higher order in ϵ, we obtain a set of equations:

()

Now, combining (8) we deduce a Korteweg-de Vries (K-dV) equation:

()

where

()

4. Numerical Analysis and Results

Generally, IA waves are low frequency electrostatic waves in which inertia is provided by ion mass and restoring force comes from electron thermal pressure. The modified ion-acoustic (mIA) waves are nothing but IA-type waves in the presence of static heavy ions. It is important to note that if we neglect the heavy ions then we get the usual IA waves. In order to analyze the IA and mIA solitary waves, we turn to (9) with the term νϕ⁽¹⁾/2τ, which is due to the effects of the nonplanar (cylindrical and spherical) geometry. An exact analytic solution of (9) is not possible. However, for clear understanding, we first briefly discuss the stationary solitary wave solution for (9) with ν = 0, though the solution is similar for both IA and mIA waves. We should note that for large value of τ, the term νϕ⁽¹⁾/2τ is negligible. So, in our numerical analysis, we start with a large value of τ (namely, τ = −14), and at this large (negative) value of τ, we choose the stationary solitary wave solution of (9) (without the term νϕ⁽¹⁾/2τ) as our initial pulse. For a moving frame moving with a speed u₀, the stationary solitary wave solution of (9) is given by

()

where the maximum amplitude ϕ_m = 3u₀/A, and the width

()

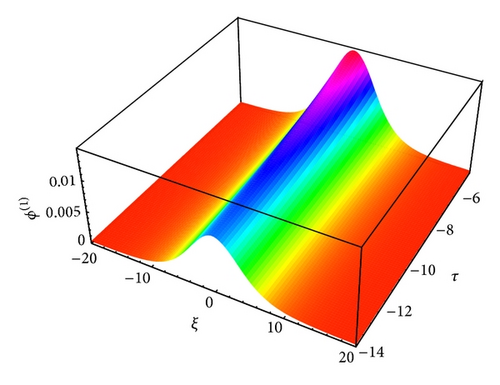
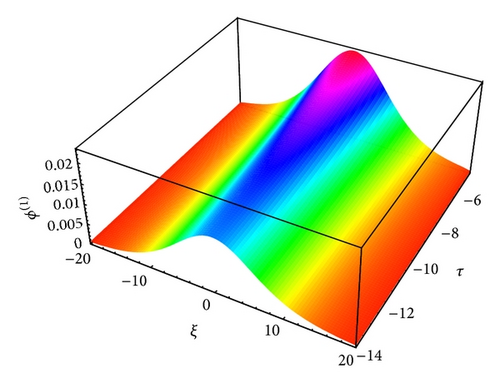
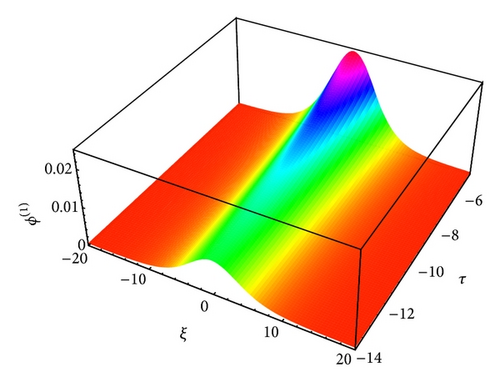
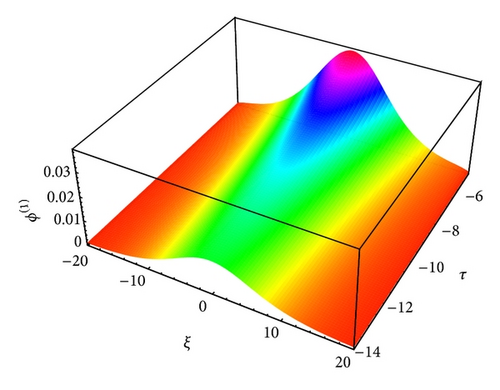
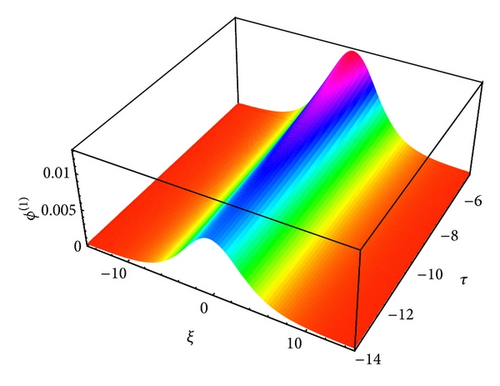
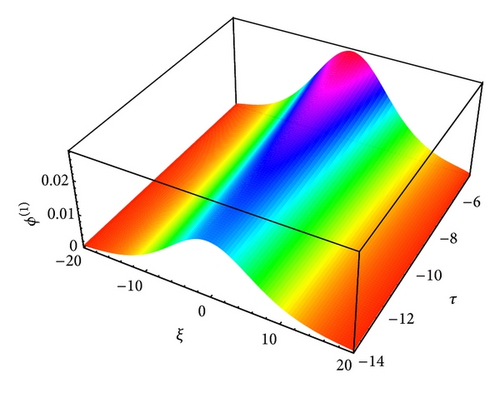
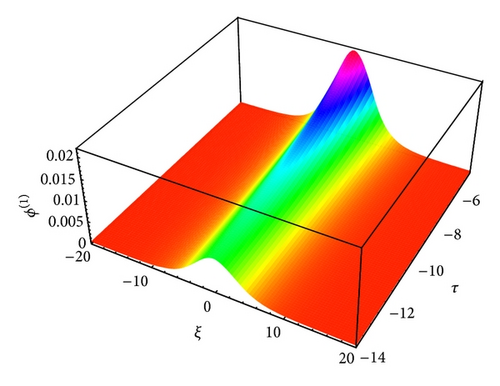
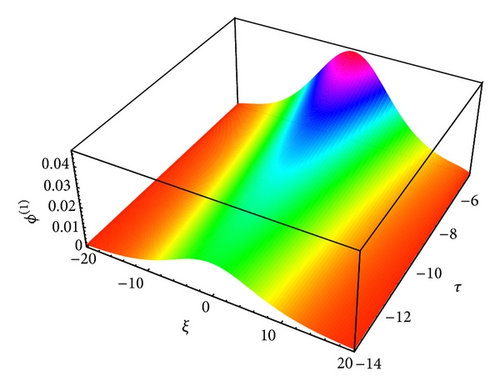
The profiles of solitary waves caused by the balance between nonlinearity and dispersion are shown in Figures 3 to 14, which show how the effects of cylindrical (ν = 1) and spherical (ν = 2) geometry modify the time-dependent IA and mIA solitary structures and how it differs from planar (ν = 0) ones.

The conditions for the existence of cylindrical and spherical solitary structures and their basic features are found to be significantly modified in the presence of nonrelativistic ions, both nonrelativistic and ultrarelativistic electrons and arbitrarily charged static heavy ions. The IA and mIA waves are modified when ion is nonrelativistic degenerate (α = 5/3) and electron is ultrarelativistic degenerate (γ = 4/3) than both electron and ion being nonrelativistic degenerate (α = γ = 5/3). The ranges (u₀ = 0.01–1 and μ = 0.2–0.6) [13–15] of plasma parameters used in this numerical analysis are very wide and correspond to space and laboratory plasma situations.

The nonlinearity has an important role as the solitary waves are caused by the balance between nonlinearity and dispersion. This is a unique phenomenon that the degree of nonlinearity is proportional to the potential of the plasma system as a highly nonlinear medium causes high electrostatic potential. We have found that the phase speed with negatively (positively) charged heavy ions for ultrarelativistic case is higher (lower) than that for nonrelativistic case (it is expected from the expression of V_p). We have also found that as time decreases the amplitude of the solitary waves in cylindrical and spherical geometry increases. It is also examined that, in spherical geometries, the amplitude is always distinctly higher than cylindrical geometries for K-dV solitons, which indicates that the density compression can be more effectively obtained in a spherical geometry. It is observed that the amplitude of the K-dV solitons is always distinctly higher for nonrelativistic case than for ultrarelativistic one. It is due to the effects of relativistic factors; that is, α > γ for ultrarelativistic case and α = γ for nonrelativistic case. We also found that the amplitude of the K-dV solitons is lower for positively charged heavy ions than for negatively charged heavy ions. Actually, this happens due to the reason that it decreases the value of the nonlinearity coefficient A. It is obvious from (12) that the height of the amplitude of the solitary structures is directly proportional to the solitary speed moving with speed u₀ and inversely proportional to A. On the other hand, (12) also implies that the width of these solitary structures is directly proportional to the square root of the constant B and inversely proportional to the solitary speed moving with speed u₀.

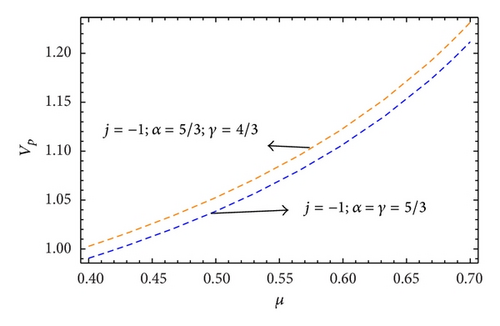
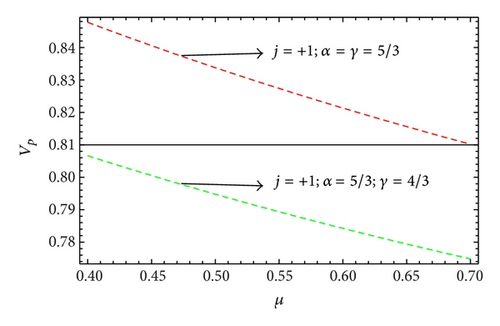
We have first graphically represented the effects of μ on the phase speed of mIA waves as shown in Figures 1 and 2. From the figures, for negatively charged static heavy ions (j = −1), we observe that the upper (dashed orange) line represents the ultrarelativistic case and the lower (dashed blue) line represents the nonrelativistic case. On the other hand, for positively charged static heavy ions (j = +1), the upper (dashed red) line represents the nonrelativistic case and the lower (dashed green) line represents the ultrarelativistic case. The profiles of IA and mIA waves for 1D planar (ν = 0) system comparing the nonrelativistic and ultrarelativistic limits are shown in Figures 3 and 4.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Showing the effects of μ on the phase speed of mIA K-dV solitons for negatively charged static heavy ions. The upper (dashed orange) line represents the ultrarelativistic case and the lower (dashed blue) line the nonrelativistic case.

The effects of degenerate electron and ion fluids and arbitrarily charged static heavy ions significantly modify the basic properties (speed, amplitude, and width) of the IA and mIA K-dV solitons. When we compare the ν = 0 case for IA wave (Figure 3), we observe that the red line represents the nonrelativistic case and the purple line represents the ultrarelativistic case. But in case of mIA wave, for negatively charged heavy ions (j = −1), we found that the upper orange line represents the ultrarelativistic case and the lower blue line represents the nonrelativistic case (Figure 4). On the other hand, for positively charged heavy ions (j = +1), the upper green line represents the nonrelativistic case and the lower pink line represents the ultrarelativistic case (Figure 4). After that, we observe the ν = 1 and ν = 2 case for both IA (Figures 13-14) and mIA waves (Figures 5–12) comparing the nonrelativistic and ultrarelativistic limits. Finally, the results that we have found in this investigation can be summarized as follows.

(1)
The plasma system under consideration supports finite amplitude K-dV solitons, whose basic properties (polarity, amplitude, width, etc.) depend on the degenerate electrons and the arbitrarily charged stationary heavy ions number densities.
(2)
For negatively (positively) charged heavy ions, the phase speed increases (decreases) with the increase of μ (Figures 1 and 2). The phase speed is always higher (lower) for negatively (positively) charged static heavy ions for ultrarelativistic case than for nonrelativistic case.
(3)
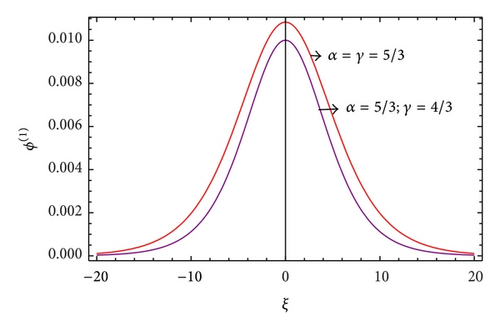
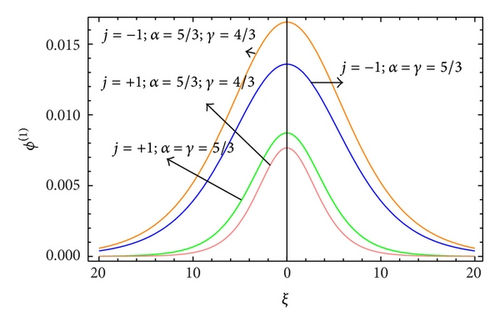
We can compare the IA and mIA solitary structures in case of planar geometry as shown in Figures 3 and 4. In these profiles, we observe that the amplitude is higher (lower) for negatively (positively) charged mIA waves than for the IA ones. It is also valid for cylindrical and spherical IA (Figures 13-14) and mIA (Figures 5–12) solitary structures.
(4)
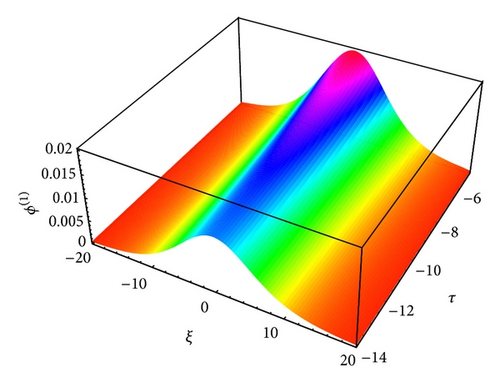
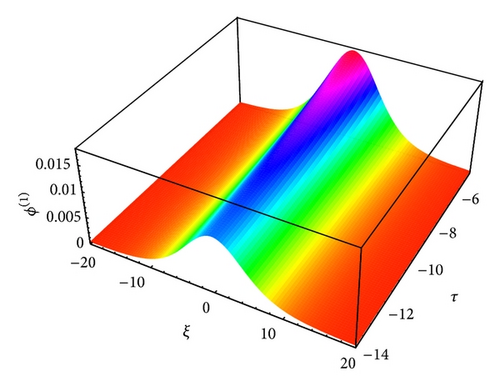
The large value of τ kills the possibility of formation of nonplanar solitons. It has been found that as the value of τ decreases the amplitude of these localized pulses increases for both IA (Figures 13-14) and mIA (Figures 5–12) waves. From the observation we can say that the amplitude of cylindrical (Figures 13 and 14 for IA and Figures 5, 6, 9, and 10 for mIA wave) K-dV solitons is larger than 1D planar (Figure 3 for IA and Figure 4 for mIA wave) ones but smaller than that of the spherical ones (Figures 7, 8, 11, and 12 for mIA wave).
(5)
From the observation of Figure 3, we can clearly say that the amplitude is lower for ultrarelativistic case than for nonrelativistic case and from Figure 4, the amplitude is higher for ultrarelativistic case than for nonrelativistic case. It is also valid for all other cylindrical and spherical graphs of IA (Figures 13-14) and mIA (Figures 5–12) waves.
(6)
The amplitude of the mIA K-dV solitons significantly differ with the polarity of heavy ions and relativistic parameters. It is found from Figure 4 that the amplitude of mIA wave in planar case is always higher (lower) for negatively (positively) charged heavy ions for both nonrelativistic and ultrarelativistic limits which is also valid in nonplanar case (Figures 5–12).

5. Discussion

We have studied the nonlinear propagation of IA and mIA solitary waves in an unmagnetized, collisionless dense plasma (containing both nonrelativistic and ultrarelativistic degenerate electrons, nonrelativistic degenerate ions, and arbitrarily charged static heavy ions). The degenerate electron and ion number densities and arbitrarily charged static heavy ions significantly modify the basic properties of the solitary waves. It is also found that the amplitude of the solitary waves has been modified by the term μ. In our numerical analysis, we have tried to give the idea of the variation among nonrelativistic and ultrarelativistic degenerate plasma pressure, IA and mIA solitary structures in case of planar and nonplanar geometry which makes our present work significant to understand the localized electrostatic disturbances in many space and astrophysical plasma environments (namely, white dwarfs, neutron stars, compact planets like massive Jupiter, other exotic dense stars, and black holes). The relativistic effects of the compact objects such as white dwarf stars make them gravitationally unstable for masses larger than about 1.4 solar masses [31] and formation of neutron stars begins. This investigation would be useful to study the effects of degenerate pressure in interstellar and space plasmas [32], particularly in stellar polytropes [33], hadronic matter and quark-gluon plasma [34], protoneutron stars [35], dark-matter halos [36], and so forth. Our present investigation is a theoretical work which is applicable for matter under extreme conditions, for example, IA and mIA solitary waves propagation in the interior of compact objects [1, 2] where the planar and nonplanar geometry, arbitrarily charged static heavy ions, inertial ions, and degenerate plasma pressure are taken into account. This theory could be rigorously important for global nonlinear models of astrophysical compact objects.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

References

1 Shapiro S. L. and Teukolsky S. A., Black Holes, White Dwarfs and Neutron Stars: The Physics of Compact Objects, 1983, John Wiley & Sons, New York, NY, USA.
10.1002/9783527617661
Google Scholar
2 Harding A. K. and Lai D., Physics of strongly magnetized neutron stars, Reports on Progress in Physics. (2006) 69, no. 9, https://doi.org/10.1088/0034-4885/69/9/R03.
10.1088/0034-4885/69/9/R03
Web of Science® Google Scholar
3 Temerin M., Cerny K., Lotko W., and Mozer F. S., Observations of double layers and solitary waves in the auroral plasma, Physical Review Letters. (1982) 48, no. 17, 1175–1179, https://doi.org/10.1103/PhysRevLett.48.1175, 2-s2.0-0001419883.
10.1103/PhysRevLett.48.1175
Web of Science® Google Scholar
4 Boström R., Gustafsson G., Holback B., Holmgren G., Koskinen H., and Kintner P., Characteristics of solitary waves and weak double layers in the magnetospheric plasma, Physical Review Letters. (1988) 61.
10.1103/PhysRevLett.61.82
PubMed Web of Science® Google Scholar
5 Dovner P. O., Eriksson A. I., Bostrom R., and Holback B., Freja multiprobe observations of electrostatic solitary structures, Geophysical Research Letters. (1994) 21, no. 17, 1827–1830, https://doi.org/10.1029/94GL00886, 2-s2.0-0028483964.
10.1029/94GL00886
Web of Science® Google Scholar
6 Ikezi H., Tailor R. J., and Baker D. R., Formation and interaction of ion-acoustic solitions, Physical Review Letters. (1970) 25, article 11, https://doi.org/10.1103/PhysRevLett.25.11.
10.1103/PhysRevLett.25.11
Web of Science® Google Scholar
7 Washimi H. and Taniuti T., Propagation of ion-acoustic solitary waves of small amplitude, Physical Review Letters. (1966) 17, no. 19, 996–998, https://doi.org/10.1103/PhysRevLett.17.996, 2-s2.0-4243844357.
10.1103/PhysRevLett.17.996
CAS Web of Science® Google Scholar
8 Roy N., Tasnim S., and Mamun A. A., Solitary waves and double layers in an ultra-relativistic degenerate dusty electron-positron-ion plasma, Physics of Plasmas. (2012) 19, no. 3, 033705, https://doi.org/10.1063/1.3688877, 2-s2.0-84861642842.
10.1063/1.3688877
CAS Web of Science® Google Scholar
9 Nahar L., Zobaer M. S., Roy N., and Mamun A. A., Ion-acoustic K-dV and mK-dV solitons in a degenerate electron-ion dense plasma, Physics of Plasmas. (2013) 20, 022304, https://doi.org/10.1063/1.4790519.
10.1063/1.4790519
CAS Web of Science® Google Scholar
10 van Albada G. B., On the origin of the heavy elements, Astrophysical Journal. (1947) 105, https://doi.org/10.1086/144914.
10.1086/144914
Web of Science® Google Scholar
11 Chandrasekhar S., The density of white Dwarf stars, Philosophical Magazine. (1931) 11, 592–596.
10.1080/14786443109461710
Web of Science® Google Scholar
12 Chandrasekhar S., Stellar configurations with degenerate cores, Monthly Notices of the Royal Astronomical Society. (1935) 95.
Google Scholar
13 Hossen M. R., Nahar L., and Mamun A. A., Roles of arbitrarily charged heavy ions and degenerate plasma pressure in cylindrical and spherical IA shock waves, Physica Scripta. (2014) 89, no. 10, 105603.
10.1088/0031-8949/89/10/105603
Web of Science® Google Scholar
14 Mamun A. A. and Shukla P. K., Solitary waves in an ultrarelativistic degenerate dense plasma, Physics of Plasmas. (2010) 17, no. 10, 104504, https://doi.org/10.1063/1.3491433, 2-s2.0-78149249274.
10.1063/1.3491433
Web of Science® Google Scholar
15 Zobaer M. S., Roy N., and Mamun A. A., DIA solitary and shock waves in dusty multi-ion dense plasma with arbitrary charged dust, Journal of Modern Physics. (2012) 3, no. 8, 755–761.
10.4236/jmp.2012.38099
Google Scholar
16 Zobaer M. S., Roy N., and Mamun A. A., Nonlinear propagation of dust ion-acoustic waves in dusty multi-ion dense plasma, Astrophysics and Space Science. (2013) 343, no. 2, 675–681, https://doi.org/10.1007/s10509-012-1290-4, 2-s2.0-84871924933.
10.1007/s10509-012-1290-4
CAS Web of Science® Google Scholar
17 Hossain M. M., Mamun A. A., and Ashrafi K. S., Cylindrical and spherical dust ion-acoustic Gardner solitons in a quantum plasma, Physics of Plasmas. (2011) 18, no. 10, 103704, https://doi.org/10.1063/1.3646738, 2-s2.0-80655125524.
10.1063/1.3646738
Web of Science® Google Scholar
18 Chandra S., Paul S. N., and Ghosh B., Electron-acoustic solitary waves in a relativistically degenerate quantum plasma with two-temperature electrons, Astrophysics and Space Science. (2013) 343, no. 1, 213–219, https://doi.org/10.1007/s10509-012-1097-3.
10.1007/s10509-012-1097-3
CAS Web of Science® Google Scholar
19 Akbari-Moghanjoughi M., Nonlinear ion waves in Fermi-Dirac pair plasmas, Physics of Plasmas. (2011) 18, 012701, https://doi.org/10.1063/1.3533425.
10.1063/1.3533425
CAS Web of Science® Google Scholar
20 Chandra S. and Ghosh B., Modulational instability of electron-acoustic waves in relativistically degenerate quantum plasma, Astrophysics and Space Science. (2012) 342, no. 2, 417–424, https://doi.org/10.1007/s10509-012-1186-3.
10.1007/s10509-012-1186-3
CAS Web of Science® Google Scholar
21 Akbari-Moghanjoughi M., Comment on “the effects of Bohm potential on ion-acoustic solitary waves interaction in a nonplanar quantum plasma” [Phys. Plasmas 17, 082307 (2010)], Physics of Plasmas. (2010) 17, no. 11, 114701, https://doi.org/10.1063/1.3494544, 2-s2.0-78650300149.
10.1063/1.3494544
Web of Science® Google Scholar
22 Manfredi G., How to model quantum plasmas, Fields Institute Communications. (2005) 46, 263–287.
Web of Science® Google Scholar
23 Brodin G. and Marklund M., Spin magnetohydrodynamics, New Journal of Physics. (2007) 9, article 277, https://doi.org/10.1088/1367-2630/9/8/277, 2-s2.0-34548315881.
10.1088/1367-2630/9/8/277
Web of Science® Google Scholar
24 El-Taibany W. F., Mamun A. A., and El-Shorbagy K. H., Nonlinear electromagnetic perturbations in a degenerate electron-positron plasma, Advances in Space Research. (2012) 50, no. 1, 101–107, https://doi.org/10.1016/j.asr.2012.03.022, 2-s2.0-84861201155.
10.1016/j.asr.2012.03.022
CAS Web of Science® Google Scholar
25 Mendonca J. T. and Serbeto A., Volkov solutions for relativistic quantum plasmas, Physical Review E. (2011) 83, 026406, https://doi.org/10.1103/PhysRevE.83.026406.
10.1103/PhysRevE.83.026406
CAS Web of Science® Google Scholar
26 Masood W. and Eliasson B., Electrostatic solitary waves in a quantum plasma with relativistically degenerate electrons, Physics of Plasmas. (2011) 18, no. 3, 034503, https://doi.org/10.1063/1.3556122, 2-s2.0-79953663649.
10.1063/1.3556122
CAS Web of Science® Google Scholar
27 Shukla P. K., Mamun A. A., and Mendis D. A., Nonlinear ion modes in a dense plasma with strongly coupled ions and degenerate electron fluids, Physical Review E. (2011) 84, 026405, https://doi.org/10.1103/PhysRevE.84.026405.
10.1103/PhysRevE.84.026405
CAS Web of Science® Google Scholar
28 Zeba I., Moslem W. M., and Shukla P. K., Ion solitary pulses in warm plasmas with ultrarelativistic degenerate electrons and positrons, Astrophysical Journal. (2012) 750, no. 1, article 72, https://doi.org/10.1088/0004-637X/750/1/72, 2-s2.0-84859902590.
10.1088/0004-637X/750/1/72
Web of Science® Google Scholar
29 Zobaer M. S., Roy N., and Mamun A. A., Ion-acoustic shock waves in a degenerate dense plasma, Journal of Plasma Physics. (2013) 79, no. 1, 65–68, https://doi.org/10.1017/S0022377812000700, 2-s2.0-84872614020.
10.1017/S0022377812000700
Web of Science® Google Scholar
30 Maxon S. and Viecelli J., Spherical Solitons, Physical Review Letters. (1974) 32, no. 1, 4–6, https://doi.org/10.1103/PhysRevLett.32.4, 2-s2.0-0005290891.
10.1103/PhysRevLett.32.4
Web of Science® Google Scholar
31 Eliasson B. and Shukla P. K., The formation of electrostatic shocks in quantum plasmas with relativistically degenerate electrons, Europhysics letters. (2011) 97.
Google Scholar
32 Ferro F., Lavagno A., and Quarati P., Non-extensive resonant reaction rates in astrophysical plasmas, European Physical Journal A. (2004) 21, no. 3, 529–534, https://doi.org/10.1140/epja/i2004-10006-0, 2-s2.0-6344294718.
10.1140/epja/i2004-10006-0
CAS Web of Science® Google Scholar
33 Plastino A. R. and Plastino A., Stellar polytropes and Tsallis′ entropy, Physics Letters A. (1993) 174, no. 5-6, 384–386, https://doi.org/10.1016/0375-9601(93)90195-6, MR1209076, 2-s2.0-0008892140.
10.1016/0375-9601(93)90195-6
Web of Science® Google Scholar
34 Gervino G., Lavagno A., and Pigato D., Nonextensive statistical effects in the quark-gluon plasma formation at relativistic heavy-ion collisions energies, Central European Journal of Physics. (2012) 10, no. 3, 594–601, https://doi.org/10.2478/s11534-011-0123-3.
10.2478/s11534-011-0123-3
CAS Google Scholar
35 Lavagno A. and Pigato D., Nonextensive statistical effects in protoneutron stars, European Physical Journal A. (2011) 47, no. 4, article 52, https://doi.org/10.1140/epja/i2011-11052-1, 2-s2.0-80054804939.
10.1140/epja/i2011-11052-1
Web of Science® Google Scholar
36 Féron C. and Hjorth J., Simulated dark-matter halos as a test of nonextensive statistical mechanics, Physical Review E. (2008) 77, 022106.
10.1103/PhysRevE.77.022106
CAS Web of Science® Google Scholar

Citing Literature

All articles

Planar and Nonplanar Solitary Waves in a Four-Component Relativistic Degenerate Dense Plasma

Abstract

1. Introduction

2. Governing Equations

3. Derivation of K-dV Equation

4. Numerical Analysis and Results

5. Discussion

Conflict of Interests

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Planar and Nonplanar Solitary Waves in a Four-Component Relativistic Degenerate Dense Plasma

Abstract

1. Introduction

2. Governing Equations

3. Derivation of K-dV Equation

4. Numerical Analysis and Results

5. Discussion

Conflict of Interests

References

Citing Literature

Figures

References

Related

Information