Journal of Computational Methods in Physics
Volume 2014, Issue 1 650365
Research Article
Open Access

Static Kirchhoff Rods under the Action of External Forces: Integration via Runge-Kutta Method

Ademir L. Xavier Jr., 

Corresponding Author

Ademir L. Xavier Jr.

Centro de Pesquisas Avancadas Wernher von Braun, Avendia Perimetral Norte 301, Alphaville, 13098-381 Campinas, SP, Brazil

Search for more papers by this author
First published: 09 January 2014
https://doi.org/10.1155/2014/650365
Academic Editor: Marta B. Rosales

Abstract

This paper shows how to apply a simple Runge-Kutta algorithm to get solutions of Kirchhoff equations for static filaments subjected to arbitrary external and static forces. This is done by suitably integrating at once Kirchhoff and filament reference system equations under appropriate initial boundary conditions. To show the application of the method, we display several numerical solutions for filaments including cases showing the effect of gravity.

1. Introduction

Filamentary bodies such as rods, ribbons, and wires are present in many scales from microscopic to astrophysical bodies. Marine cables [1], hair beams [2], rubber bands, microfibers [3], nanowires [4], and DNA molecules [5] share common dynamics, which is testified by the onset of rich elastic phenomena such as buckling, coiling, and looping [6]. The writhing instability for example [7, 8] is a looping process in which the spatial configuration of an elastic filament changes remarkably as a response to an applied external torque, the change itself as a minimization process of the filament elastic energy.

The dynamics of filamentary bodies has been the subject of extensive research in continuum mechanics with the aim of establishing either exact or approximate solutions for thin filaments. The theory itself started with Kirchhoff [9, 10] in 1892 and Clebsch and Love [11] who considered small deformation of thin rods within the elastic range. The theory was developed under special assumptions that later became the approximations adopted by the so-called simple bending and torsion theory [12]. Although the deformations of infinitesimal portions of a rod in the theory may be small, the overall deformation is quite large and allows the coiling and looping phenomena above mentioned.

Exact solutions of Kirchhoff equations for static rods are well known. Shi and Hearst found the most general analytical solution to the static Kirchhoff rod, which they called helix on a linear helix [13]. Nizzete and Goriely [14] used the equivalence between the static Kirchhoff equations for rods with circular cross-sections and the Euler equations for spinning tops to provide a classification of all different equilibrium solutions for a filament. Chouaieb et al. [15] completed the study of existence and stability of helical structures within the Kirchhoff rod model. Goriely and Tabor [7, 16] developed a dynamical method to study the stability of equilibrium solutions of the Kirchhoff rod model, based on a time-dependent perturbation scheme, thus providing a framework for classification of new solutions. This method has been used, for example, to study DNA rings [17, 18] and nanowires [19] under large stresses.

In biology and nanoscience, for example, most of the interesting filaments are the ones subject to diverse boundary conditions. Tobias et al. [20] derived analytic expressions for the equilibrium configurations of filaments representing long segments of a DNA double helix under different end conditions. da Fonseca et al. [19, 21] recently used the Kirchhoff model to propose schemes for the study of the elastic properties of nanowires and nanosprings. McMillen and Goriely [22] obtained equilibrium solutions for the tendril perversion structure within the framework of the Kirchhoff rod model, which are heteroclinic orbits joining asymptotically two helices with opposite torsion. Gottlieb and Perkins [23] investigated spatially complex forms in a BVP governing the equilibrium of slender cables subjected to thrust, torsion and gravity. In a very comprehensive work, Powers [24] treats the dynamics of filaments in viscous fluids and solves some interesting cases.

Despite the success of the above examples of equilibrium solutions of Kirchhoff model subject to some particular types of boundary conditions, boundary value problems are still a great challenge in the study of the static and dynamics of filaments. The main approach to find out equilibrium solutions for filaments subject to arbitrary boundary conditions is to rely on numerical computation. Examples are the use of finite element methods to obtain the equilibrium solutions of supercoiled DNAs [25], numerical package tools to solve differential equations based on a Hamiltonian formalism of the rod model [26], and a method of linearization of Kirchhoff equations, to find equilibrium solutions of open rods with fixed ends [27].

In this paper, we explore the use of straightforward methods, as the use of implicit or explicit iterative methods such as Runge-Kutta of a given order subjected to boundary conditions, to solve static filaments under the action of (static) external forces. This is done by a numerical procedure in which the Kirchhoff equations and the reference frame of the filament centerline are combined to solve the boundary value problem. The organization of the paper is as follows: we first make an introduction to the general Kirchhoff equations of rods (Section 2) and show how to use the external force to obtain a transformation matrix that couples the system of Kirchhoff equations to the filament reference frame (Sections 2.1 and 2.2). In Section 2.2 we introduce the general formulation of boundary value problems. In Section 3 we present numerical examples of closed and open rods subjected to boundary conditions, including illustrations of the effect of gravity in several kinds of filamentary solutions obtained in the absence of external forces. Section 4 is in fact a note on how to transform the filament problem into several types of boundary value problems. Finally, Section 5 (conclusion) summarizes our main results.

2. Kirchhoff Model for Thin Rods

In order to write the static equation for rods, we first make a short summary of the main dynamical equations of rods (Figure 1) that are valid under the following definitions and assumptions [10]: (i) a rod or filament is a 3D body in which two of the dimensions are much smaller than a third one which defines the axis or centerline of the rod; (ii) a rod is viewed as a sequence of short segments of area A which are held together by contact forces, p, between adjacent segments sharing the same elastic properties; (iii) the cross-section of a segment remains undistorted and perpendicular to the axis defined by the third dimension. The axis may be taken as the centroid of the section; (iv) displacements are always small and the breakdown of the elastic limit is never achieved. In this way, stresses and torques are always proportional to strains in full accordance with Hook′s law.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Illustration of a rod segment with cross-section area A actuated by external and contact forces.

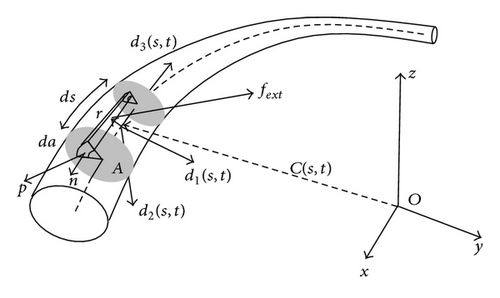
With this in mind, we considered a segment of a rod or thin filament with length ds as shown in Figure 1. A given segment can be assessed by the arclength parameter s which runs from 0 to L, the total rod length. The rod has cross-section A which is symmetrical in relation to the centroid position defined by the vector C(s, t) written in relation to a fixed frame with origin O in the laboratory.

Each segment is subject to internal and external forces which, in general, are functions of s. Internal forces p act upon the segment differential area dA and external forces fext on the differential volume element dAds. Newton′s laws for the segment can then be written as
()
()
where ρ is the material density of the rod and R(s, t) is the position of the element in the external reference system O. Equations (1) and (2) are, respectively, the conservation of linear momentum and angular momentum of the rod in which all internal forces were substituted by contact stresses on the normal ndA of the segment and the external force act upon a volume element dv.
To each segment we attach a local reference system of unitary vectors d1, d2, and d3, so that d3 is parallel to the segment axis and d1 and d2 are orthogonal to d3. These are often called Frenet-Serret basis vectors [8] and are all dependent on s and t as the rod evolves in time. Since
()

the last relations are twist and spin equations of the rod. Writing k in the d-basis, k1 and k2 are the curvature vectors and k3 is the twist density. Vector w is the spin vector and represents the angular momentum of the section in the local basis.

It is also common to separate the element position in two terms: the position r(s, t) in relation to the local reference frame given by the d-basis and the position of the segment central axis in relation to the external reference system:
()
with
()
As a consequence of the chosen basis, the centroid position is given by
()

and the curve can be followed by the time dependence of the d3 vector.

Defining the total contact force integrated on the rod section as
()
and the segment moment about the central axis as
()
the next step is to differentiate (1) and (2) with respect to s what, using (7) and (8), gives
()
Note that (9) are valid for constant density rods which are the cases to be treated here, and they can be further simplified by using definitions (4), (5), and (6) and integrating on the section area A. The result is given in terms of the local reference system, the d-basis:
()
()
with I1 and I2 the moment of inertia of the section in relation to the axis formed by the d1 and d2 vectors. To proceed further, we need a constitutive relation for the rod moment M. As usual, we write [6, 10]
()

with E and G being Young′s and the shear moduli of the material, respectively, and J the axial moment of inertia. Equation (12) was written in such a way that if k1 = 0 and k2 = 0, the filament is naturally straight.

In (10) and (11), the derivatives of F and M with respect to s can be written as
()
where we have used the summation convention. With the help of (3), we find
()
so that the equations for the static filaments (removing the terms proportional to the derivative with respect to time in (10) and (11)) read:
()
where and , i = 1,2, 3, are the components, in d-basis, of the vectors Fext and Mext, respectively, defined by
()

Note that the static condition does not imply that the force will be constant throughout the filament since there is an interaction among different components, arising from terms of the rotated coordinate system that is attached to each filament segment.

2.1. Integrals for the External Reference System

If we manage to integrate (10) and (11), we obtain a solution which is still written in the segment reference system given by the d-basis vectors. However, solutions are best understood if written in the external and fixed system represented by the origin O as in Figure 1. In particular, the integral of the third vector d3 gives the parametric curve of the centroid as stated by (6). It is possible to find a transformation that takes vectors from the fixed system to the local one and the corresponding inverse operation [14]. In general we can write
()
where e0 is a vector in Cartesian basis () of the fixed system and S(s, t) is a 3 × 3 real matrix representing a sequence of pure rotations, so that det [S(s, t)] = 1. Since
()
()
and (3) are valid for the d-basis, we have
()
()
()
with
()
()

After integration of (10) and (11), Equations (20) and (21) must be integrated in order to obtain a description of the rod in the fixed system.

If we restrict ourselves to static problems, first we obtain the solution for k by (15), then S is obtained by (20) using (23), d(s) is directly given by (17), and, finally, the centroid curve can be generated by the integration of
()
where (6) was used and now the vector C is given in the fixed () basis. The description of the filament is now complete: we have as initial condition the coordinate of one of the filament tips given by the vector
()
the orientation of the centerline of the rod at the tip with respect to the fixed system given by
()

and the s-“dynamics” given by (20) in accordance to the K matrix.

2.2. Coupling the Kirchhoff Equations to the Reference Frame System

From now on we treat static rods only, whose solutions are given by solving (15) and W = 0 which correspond to equilibrium solutions as described in [28]. These form a system of first order differential equations with initial value
()
From the point of view of the initial value problem, the set of conditions (28) generates solutions for (15). However, these solutions are “unreferenced” in as much as the s-evolution of the basis (d1, d2, d3) must still be obtained by integrating (20). In what follows, for simplicity, we will initially take all external forces as zero, Fext = 0 and Mext = 0. If we define the vector Q with components Qi, i = [1, …, 6], as
()
()
then (20) becomes
()
which is the reference system problem to be solved subjected to the initial condition
()
Rewriting the set of first order differential equations (15), Q(s) should be obtained from
()
A solution of (31) is such that the matrix S(s) is orthogonal. To show this, we note that (23) implies that Kt + K = 0, or StKtS + StKS = 0. Using (20) we find that
()
Since we choose St(0)S(0) = 1, then
()
for all s with 1 the unit matrix. We also remark that, for the t-evolution in the dynamical case, the same result holds given (21) and (24). Finally, in order to get the filament curve, the following equation, derived from (6) and (26),
()
should be solved subjected to the position of the initial filament tip C(0). Only after solving the sequence of these three sets of first order differential equations a complete solution of Kirchhoff′s problem is obtained. Such a procedure can be implemented numerically, but, instead of running each set of equations sequentially we compose the great vector
()
with 18 components. The derivative of X with respect to s will then be given by
()
subjected to the initial condition
()
Therefore, a single numerical procedure can be used to integrate the three sets of problems at once. We again emphasize the physical meaning of such approach. In order to get a complete filament solution, we must give the coordinate of the initial tip C(0), the direction of the three reference vectors that compose the basis, T(0), and the initial force and curvature vectors Q(0) in such a predefined basis. The Kirchhoff problem of rods as an initial value problem therefore spans a space with 18 dimensions. However, this does not mean that there are 18 independent values. In fact, since S(s) is orthogonal and represents a reference basis, one can parametrize S by only 3 parameters. For example, the initial orientation of a filament tip (Figure 2) at the origin may be set by d3(0) as
()
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Orientation of the d-basis vectors and the fixed reference frame. Vector d3 is always tangent to the filament curve.
with x0, y0, and z0 three real numbers. The initial vector X may be written as
()
with
()
where . In (41) the third component of d2(0) was set to zero as shown in Figure 2. Note that there is some freedom in the choice of d1(0) and d2(0). These may be chosen so as to coincide with the main axis of the filament cross-section which leads to an easy visualization of the segment orientation if the cross-section is not circular. One can also use Euler angles [18], θ, φ, and ψ, and write the initial S matrix as
()
with
()

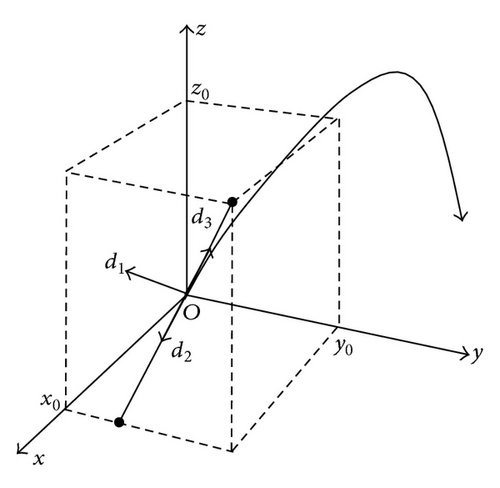
The total number of degrees of freedom in the specification of a solution is therefore 12.

3. Solving the Initial Value Problem with and without External Force

Equation (38) can be straightforwardly integrated by Runge-Kutta algorithm of nth order, [29] subjected to the initial condition (39). The method is a well-known technique of integration which symmetrically advances the solution step bystep using information of the current derivative such as the one given by (38). In the case of static filaments, the independent variable is the parameter s, which runs from 0 to L (the filament length) and plays exactly the same role of time in dynamical problems. The interaction of crossed terms, which is relevant in external forces cases, is completely taken into account through the scheme of (37). To illustrate some solutions, we use a 5th order Runge-Kutta integrator with the following initial condition [6]:
()
and I1 = I2. This produces Frenet helices with constant curvature and force and the solution for the centroid is shown in Figure 3 for the indicated values of τ. In this case, I1 = I2 = 2.0, G = 1.0, E = 0.5, κ = 1.0, L = 60.0, k1(0) = 0, k2(0) = 1, k3(0) = 0.03, F1(0) = 0, F2(0) = 0.09, F3(0) = 2.7 × 10−3, and the integration was made with 3000 points. As the value of τ is increased, the Frenet helix is distended indicating an increase in the force along the z-axis (vertical). The orientation of the initial local basis is
()
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Frenet helices for circular cross section filaments and increasing values of t. As usual, z is the vertical axis of the box.

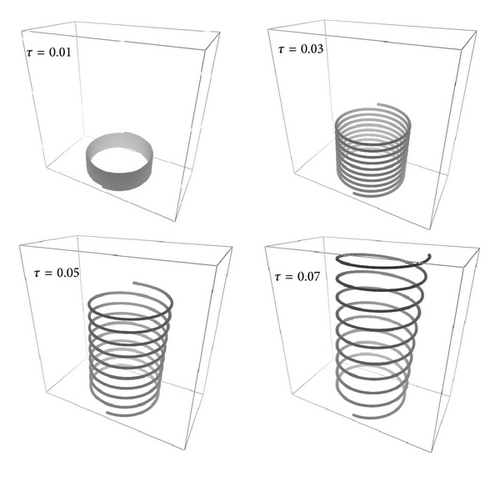
and the coil filament starts from the origin. Space periodic solutions, C(0) = C(L), can also be generated. Figure 4 contains filaments with 3000 steps with circular cross-section, I1 = I2 and the same initial orientation. The parameters used to generate each curve are as follows: (a) E = 0.2, G = 0.5, k1(0) = 0.0, k2(0) = 0.1, k3(0) = 0.1, F1(0) = 0.0, F2(0) = 0.01, F3(0) = 0.0, I1 = 1.0, L = 63.0, (b) E = 1.0, G = 2.5, k1(0) = 0.0, k2(0) = 1.3, k3(0) = 0.01, F1(0) = 0.0, F2(0) = 0.9885, F3(0) = 1.0, I1 = 2.0, L = 71.0, (c) E = 0.1, G = 2.5, k1(0) = 0.0, k2(0) = 1.3, k3(0) = 0.01, F1(0) = 0.0, F2(0) = 0.9885, F3(0) = 1.0, I1 = 2.0, L = 13.0, and (d) E = 0.2, G = 2.5, k1(0) = 0.0, k2(0) = 1.3, k3(0) = 0.01, F1(0) = 0.0, F2(0) = 0.99, F3(0) = 2.0, I1 = 2.0, L = 35.0. (a) and (b) are almost closed solutions. In order to produce them, specially tuned boundary conditions were chosen as described in [28]. In this sense, the method is unable to produce closed solutions without further tuning of boundary values and other parameters. By changing the value of Young′s modulus, the curve opens itself and becomes a complex helix as shown in Figure 4(d).

Details are in the caption following the image
Figure 4 (a)
Open in figure viewerPowerPoint
A variety of solutions for a circular cross section filament and different values of initial conditions. (a) and (b) are closed solutions. See text for the parameters of each figure; z is the vertical direction.
Details are in the caption following the image
Figure 4 (b)
Open in figure viewerPowerPoint
A variety of solutions for a circular cross section filament and different values of initial conditions. (a) and (b) are closed solutions. See text for the parameters of each figure; z is the vertical direction.
Details are in the caption following the image
Figure 4 (c)
Open in figure viewerPowerPoint
A variety of solutions for a circular cross section filament and different values of initial conditions. (a) and (b) are closed solutions. See text for the parameters of each figure; z is the vertical direction.
Details are in the caption following the image
Figure 4 (d)
Open in figure viewerPowerPoint
A variety of solutions for a circular cross section filament and different values of initial conditions. (a) and (b) are closed solutions. See text for the parameters of each figure; z is the vertical direction.

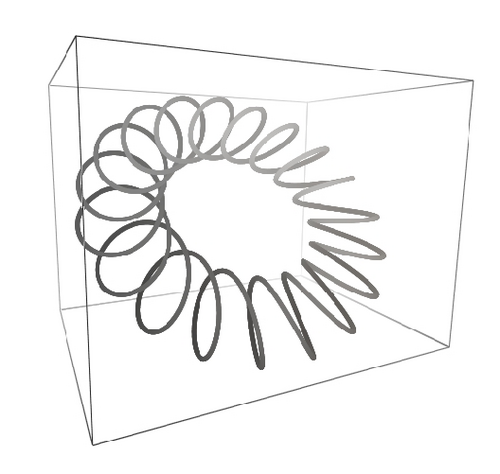
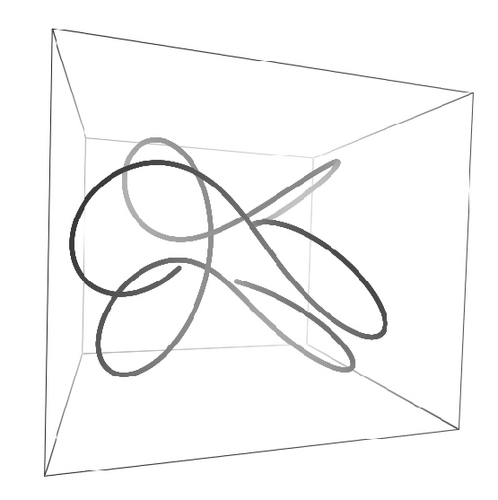
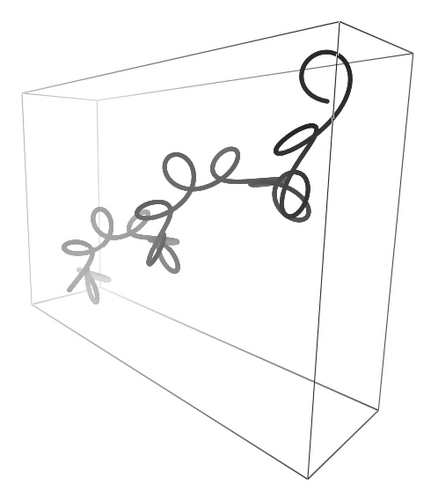
Since in the last examples, I1 = I2, then k3(s) = k3(0) for all s according to the last element of (38). Young′s modulus E multiplies I1 and I2 as shown by (15), so that the cases for which I1 ≠ I2 either represent homogeneous filaments with noncircular cross-sections or circular cross-section filaments with anisotropic bending stiffness. To illustrate this case, we show in Figure 4 a helix with I1 = 3.0 and I1 = 2.0 and decreasing values of G, the shear modulus, as indicated in the figure. For this case we have E = 1.0, k1(0) = 0.0, k2(0) = 1.0, k3(0) = 0.07, F1(0) = 0.0, F2(0) = 0.21, F3(0) = 0.0147, L = 63.0 and 3000 points. As the shear modulus decreases, the filament stretches as a response to less torsion rigidity.

General forms of external forces may be written as
()
with
()
where the α′s are real coefficients describing the dependence of the force as a function of parameter s along the rod [10]. Gravity is an example of force for which the external torque is zero, since gravity can not make the segment turn about its symmetric axis. For gravity all α′s are zero except α10, α20, and α30. We will restrict ourselves to gravity in the numerical examples that follow. For the segment, the evaluation of the first integral in (16) leads to
()
with g the gravity constant. This term must be inserted in (15), but first we need to write in terms of the d-basis. Using (17) we write
()
Therefore, using definition (30), we write (49) as
()
Equation (33) then becomes
()

Equation (52) shows the appearance of crossed terms in the integration scheme of (38). For other external forces pointing to arbitrary directions, or under the action of external torques, the same procedure should be applied by writing whatever fixed components in terms of the d-basis through (50).

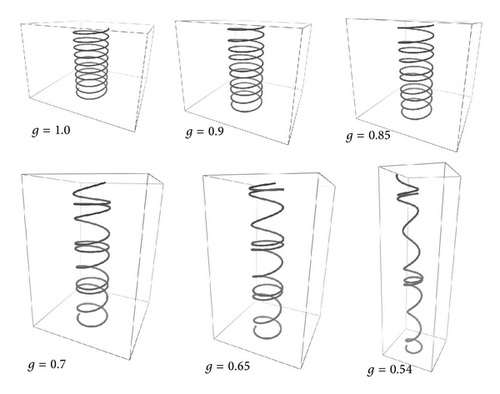
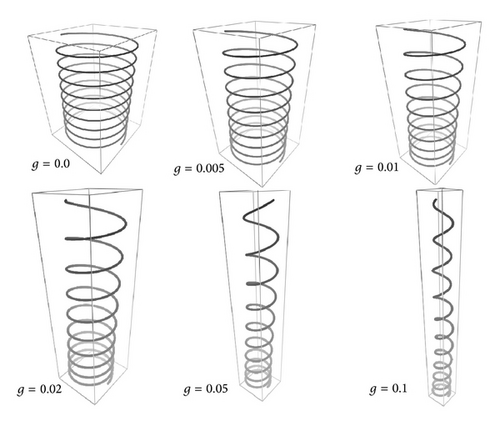
In order to illustrate gravity effects, we consider two Frenet helices with distinct orientations. In the first case (Figure 5), the gravity zero helix is vertical. The parameters of Figure 5 are as follows: E = 1.0, G = 0.5, k1(0) = 0.0, k2(0) = 2.0, k3(0) = 0.1, F1(0) = 0.0, F2(0) = 0.0, F3(0) = 0.0, I1 = 1.0, I2 = 1.0, L = 30.0, r = 1.0, A = 1.0 and g is varied as indicated in the figure. These simulations were obtained with 3000 steps. We note that, as g is increased, the helix distorts itself resembling a “curly-hair” filament. The helix pitch at the lower turns is smaller than the upper ones, because these must support most of the filament weight and are therefore more stretched.

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Effect of anisotropy in a filament with decreasing shear modulus. The original I1 = I2 case is a classic Frenet helix with g = 1.0. For all cases above I1 = 3.0 and I2 = 2.0. As g decreases the filament becomes less rigid against torsion. The parameters used to generate each curve are in the text; z is the vertical direction.

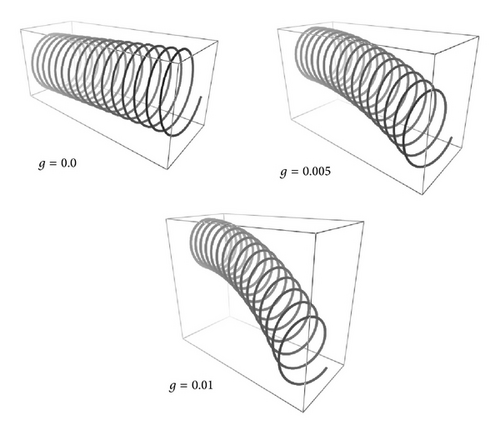
Another possible solution comes from horizontal helices under the action of gravity. In Figure 7, a sequence of Frenet helix is shown with the same initial conditions of Figure 6 but with L = 50.0. The orientation of d(0) is now orthogonal to the previous case so that gravity is orthogonal to the helix main axis. The natural spring is deformed toward −z as intuitively expected by simple experiments with coils and ribbons.

Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
“Curly-hair” solutions or Frenet helices under the action of gravity for increasing values of g, stretching the filament vertically. Gravity points downward in the −z direction. The parameters used to generate each curve are in the text.
Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Horizontal Frenet helix under the action of gravity. The parameters are the same as in Figure 6, with exception of d(0) which is orthogonal to the one used in previous examples.

4. Note about Static Filament Solutions as a Boundary Value Problem

The initial value problem defined by (38) and (39) can be cast into a variety of boundary value problems. Due to space limitations, it is not in the scope of this paper to fully describe the variety of Cauchy′s problems arising from filaments in the Kirchhoff approximation, even in its purely static cases. However, in order to give some directions on how solutions could be built, we briefly make here some very straightforward comments. As is known [29], a problem consisting of a set of N first order differential equations subjected to N initial conditions can be transformed to a boundary value problem with n (n < N) initial conditions and N − n final conditions. Let us first define the initial value problem by the sequence of conditions (C′, T′, F′, k′) in which we explicitly represent Q′ (29) by its constituents F′ and k′ (note that now subscripts do not represent time differentiation). Then, the following sequence of boundary value problems examples can be written as
()
()
()
()
()
()
In order to solve Problem (53) for example, one can use the shooting method by searching the {k′} space for a solution which minimizes the discrepancy vector
()
The search is operated iteratively for the (i + 1)-step by the globally convergent Newton-Raphson method [29] and by giving an initial
()
such that
()
where Bi is the value of (59) evaluated at the i-step and J is the Jacobian matrix
()
evaluated numerically for the current step. In order to provide a numerical example, we again go back to Figure 4(a) and consider the problem of “closing” a single loop. We fix L = 62.835 and let I1 = I2 = 1.0 and E = 0.2, G = 0.5, k1(0) = 0.0, k2(0) = 0.1, k3(0) = 0.1, F1(0) = 0.0, F2(0) = 0.01, F3(0) = 0.0. Instead of calculating ∂Bi/∂kj, we determine the surface generated by |B(k′)| and inspect the topology of ∂Bi/∂kj on the plane since k3 is constant. The following set of points on this plane
()
with m = 20, Δk1 = Δk2 = 0.001, will result in Figure 8(a) while a magnified view is shown with Δk1 = Δk2 = 0.00001 in Figure 8(b). These plots exhibit a clear minimum corresponding to the pair that minimizes |B(k′)|.
Details are in the caption following the image
Figure 8 (a)
Open in figure viewerPowerPoint
Plots of for 20 × 20 solutions of Kirchoff loops around k1(i = 10) = 0.0, k2(j = 10) = 0.1 with i and j given by (63). In (a), Δk1 = Δk2 = 0.001 and in (b) Δk1 = Δk2 = 0.00001.
Details are in the caption following the image
Figure 8 (b)
Open in figure viewerPowerPoint
Plots of for 20 × 20 solutions of Kirchoff loops around k1(i = 10) = 0.0, k2(j = 10) = 0.1 with i and j given by (63). In (a), Δk1 = Δk2 = 0.001 and in (b) Δk1 = Δk2 = 0.00001.
Problems (54)–(58) can be solved by the same reasoning. However, for problems (57) and (58) the actual number of search variable is six because of the parametric dependency of matrix S as stated earlier. Let us admit that α, β, and γ are the set p of three parameters. These can be the x0, y0, and z0 of (40) or the Euler angles. For problem (58) one can write the discrepancy vector as
()
which can be expanded as a function T′ and k′
()
However, one can also write
()
so that
()
Imposing the condition B(T′ + δT′, k′ + δk′) = 0 to get a solution, we find the equation system
()

which is essentially similar to (61) with an extended Jacobian.

5. Conclusions

In this paper we have obtained static solutions for Kirchhoff′s equations by numerical integration, using a scheme in which both Kirchhoff and reference system equations are integrated at once. By incorporating additional dimensions, the final vector that describes the filament curve is also obtained. The scheme allows a quick and easy determination of solutions under the action of external (static) forces. These appear as interaction terms in both force and moment equations, (10), provided the components of force and torque are expressed in the local reference system. This was the case of gravity and is also the case of many other external forces such as the centrifugal acceleration for a filament in a rotating system, the electric force for a charged filament [30], or a magnetized filament in the presence of magnetic fields [31].

In order to obtain solutions, we have treated the integration of the static equations as initial and boundary value problems. As an initial value problem, the filaments can be generated as solutions of a set of first order differential equations subjected to 18 initial values. Some of these values are linked to each other (due to the parametric dependency of the S matrix), so that the actual number of degrees of freedom for the initial values is 12. This sets the maximum number of dimensions in the constraints for the boundary value version of the filament problem. As a boundary value problem, several types of initial and final constraints can be written.

In deriving Kirchhoff′s equations for static filaments, we have kept the filament density constant. The effect of nonhomogeneities in rods can be easily incorporated into Runge-Kutta system as an additional term in both force and moment laws. The same is valid for wires with nonuniform elastic constants such as E and G. In summary, several classes of static solutions can be stud by using the approach here presented.

Conflict of Interests

The author declares that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

The author would like to thank Christine Fernandes for the preparation of the LaTeX version of this paper, Marcus A. M. de Aguiar and Alexandre F. da Fonseca (IFGW/UNICAMP) for useful discussions.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.