International Journal of Engineering Mathematics

Volume 2014, Issue 1 628041

Research Article

Open Access

Design of Robust Output Feedback Guaranteed Cost Control for a Class of Nonlinear Discrete-Time Systems

Yan Zhang,

Yan Zhang

School of Science, Tianjin Polytechnic University, Tianjin 300387, China tjpu.edu.cn

Search for more papers by this author

Yali Dong,

Corresponding Author

Yali Dong

[email protected]

School of Science, Tianjin Polytechnic University, Tianjin 300387, China tjpu.edu.cn

Search for more papers by this author

Tianrui Li,

Tianrui Li

School of Science, Tianjin Polytechnic University, Tianjin 300387, China tjpu.edu.cn

Search for more papers by this author

Yan Zhang,

Yan Zhang

School of Science, Tianjin Polytechnic University, Tianjin 300387, China tjpu.edu.cn

Search for more papers by this author

Yali Dong,

Corresponding Author

Yali Dong

[email protected]

School of Science, Tianjin Polytechnic University, Tianjin 300387, China tjpu.edu.cn

Search for more papers by this author

Tianrui Li,

Tianrui Li

School of Science, Tianjin Polytechnic University, Tianjin 300387, China tjpu.edu.cn

Search for more papers by this author

First published: 10 September 2014

https://doi.org/10.1155/2014/628041

Academic Editor: Yurong Liu

Share a link

Email
Wechat
Bluesky

Abstract

This paper investigates static output feedback guaranteed cost control for a class of nonlinear discrete-time systems where the delay in state vector is inconsistent with the delay in nonlinear perturbations. Based on the output measurement, the controller is designed to ensure the robust exponentially stability of the closed-loop system and guarantee the performance of system to achieve an adequate level. By using the Lyapunov-Krasovskii functional method, some sufficient conditions for the existence of robust output feedback guaranteed cost controller are established in terms of linear matrix inequality. A numerical example is provided to show the effectiveness of the results obtained.

1. Introduction

In control theory and practice, one of the most important open problems is the static output feedback (SOF) problem. The main principle of the SOF control is to utilize the measured output to excite the plant. Since the controller can be easily implemented in practice, the SOF control has attracted a lot of attention over the past few decades and has been applied to many areas such as economic, communication, and biological systems [1, 2]. The goal of design SOF controller is to ensure asymptotically stable or exponential stable of the original system [3]. However, in many practical systems, controller designed is to not only ensure asymptotically or exponentially stable of the system but also guarantee the performance of system to achieve an adequate level. One method of dealing with this problem is the guaranteed cost control first introduced by Chang and Peng [4]. This method has the advantage of providing an upper bound on a given performance index and thus the system performance degradation is guaranteed to be no more than this bound. Based on this idea, a lot of significant results have been addressed for continuous-time systems in [5–7] and for discrete-time systems in [8].

It is well known that time-delays as well as parameter uncertainties frequently lead to instability of systems. Moreover, the existing of time-delays and uncertainties make the system more complex [9, 10].

In the past studies for guaranteed cost control, almost most of the articles considered linear systems [11, 12]. However, in majority dynamic systems, the nonlinear perturbations appear more and more frequently. Therefore, we not only deal with the time-varying delays and uncertainties, but also deal with the nonlinearities. Difficulties then arise when one attempts to derive exponential stabilization conditions. Hence in this case, the methods in linear systems [11, 12] can not be directly applied to nonlinear systems. This calls for a fresh look at the problem with an improved Lyapunov-Krasovskii functionals and a new set of LMI conditions. In this paper, we aim to design robust static output feedback guaranteed cost controller for a class of nonlinear discrete-time systems with time-varying delays. By constructing a set of improved Lyapunov-Krasovskii functionals, a new criterion for the existence of robust static output feedback guaranteed cost controller is established and described in terms of linear matrix inequality. A numerical example is provided to show the effectiveness of the results obtained.

Notations. In this paper, a matrix A is symmetric if A = A^T. λ_max⁡(A)(λ_min⁡(A)) denotes the maximum (minimum) value of the real parts of eigenvalues of A. The symmetric terms in a matrix are denoted by *. X > 0 (resp., X ≥ 0), for X ∈ R^n×n, means that the matrix is real symmetric positive definite (resp., positive semidefinite). N⁺ denotes the set of all real nonnegative integers.

2. Preliminaries

Consider the following control system:

(1)

where x(k) ∈ Rⁿ is the state vector, y(k) ∈ R^r is the observation output, and u(k) ∈ R^m is the control intput. A, A₁, B, F, G, C, and C₁ are given constant matrices with appropriate dimensions. ΔA(k), ΔA₁(k) are the time-varying parameter uncertainties that are assumed to satisfy the following admissible condition:

(2)

where M, N₁, and N₂ are some given constant matrices with appropriate dimensions. The positive integers d(k) and h(k) are time-varying delays satisfying

(3)

where d, h are known positive integers. f(x(k)) ∈ Rⁿ and g(x(k − h(k)) ∈ Rⁿ are unknown nonlinear functions, assumed as

(4)

where β₁, β₂ are known positive integers and L₁, L₂ are known real matrices. The initial condition ϕ = (ϕ_−τ, ϕ_−τ+1, …, ϕ₀) ∈ R^(τ+1)n with the norm

(5)

where τ = max⁡{h, d}.

The corresponding cost function is as follows:

(6)

where S, S₁, S₂, and R are given symmetric positive definite matrices with appropriate dimensions.

Substituting the output feedback controller u(k) = Ky(k) into system (1), we have

(7)

where

and

The objective of this paper is to design an output feedback controller u(k) = Ky(k) for system (1) and cost function (6) such that the resulting closed-loop system is robust exponentially stable with an upper bound for cost function (6).

We first give the following definitions, which will be used in the next theorems and proofs.

Definition 1. Given α > 0, the closed-loop system (7) is said to be robust exponentially stable with a decay rate α, if there exists scalars σ > 0 such that for every solution x(k, ϕ) of the system satisfies the condition:

(8)

Definition 2. For system (1) and cost function (6), if there exist a static output feedback control law u^*(k) and a positive constant J^* such that the closed-loop system (7) is robust exponentially stable with a decay rate α and the value (6) satisfies J ≤ J^*, then J^* is said to be a guaranteed cost index and u^*(k) is said to be a robust output feedback guaranteed cost control law of the system.

The following lemmas are essential in establishing our main results.

Lemma 3 (see [11].)For any x, y ∈ Rⁿ, and positive symmetric definite matrix N ∈ R^n×n, we have

(9)

Lemma 4 (Schur complement lemma [13]). Given constant matrix X, Y, and Z with appropriate dimensions satisfying X = X^T, Y = Y^T > 0. Then X + Z^TY⁻¹Z < 0 if and only if .

3. Main Results

In this section, by constructing a new set of Lyapunov-Krasovskii functionals, we give a sufficient condition for the existence of robustly output feedback guaranteed cost control for system (1).

Theorem 5. For a given scalar α > 0, the control u(k) = Ky(k) is a robustly static output feedback guaranteed cost controller for nonlinear system (1), if there exist symmetric positive definite matrices P, Q₁, Q₂, R₁, R₂, and K, arbitrary matrix N, and scalars ε₁ ≥ 0, ε₂ ≥ 0, such that the following LMI holds:

(10)

where

(11)

and the guaranteed cost value is given by J^* = μ₂∥ϕ∥², where

(12)

Proof. We first introduce the new variable z(k) = e^αkx(k). The closed-loop system (7) is reduced to

(13)

where

and

Associated with (2), the above equality is reduced to

(14)

where

(15)

(16)

(17)

Consider a Lyapunov-Krasovskii functional candidate for the closed-loop system (14) as

(18)

where

(19)

Calculating the difference of V(k) we have

(20)

(21)

(22)

Combine (21) and (22), we have

(23)

Similarly, we can get

(24)

Therefore, from (17)–(24), we have

(25)

Multiplying 2z^T(k + 1)N both sides of the identity (14),

(26)

Note that for any ε₁ ≥ 0, ε₂ ≥ 0, it follows from (16) to (17)

(27)

Substituting (26)-(27) into (25), we have

(28)

Dealing with partial idem in (28) using Lemma 3, it follows

(29)

Similarly, we have

(30)

Adding the following relation to inequality (28)

(31)

where

, and

, and using

(32)

we can get

(33)

where ξ(k) = [z^T(k) z^T(k + 1) z^T(k − d(k)) z^T(k − h(k))

and

(34)

By Lemma 4, the condition Ω < 0 is equivalent to LMI (10). Therefore, from (33) it follows that

(35)

which implies that V(k) ≤ V(0), ∀k ∈ N⁺.

We can easily get

(36)

where ∥z_k∥ = max⁡{∥z(k − τ)∥, …, ∥z(k)∥}, μ₁ = λ_min⁡(P),

(37)

From (35) and (36), we can get

(38)

Using the relation z(k) = e^αkx(k), we can get

(39)

Therefore, the closed-loop system (7) is exponentially stable. Next we will find the guaranteed cost value, from (33), we can get

(40)

Summing up both sides of (40) from 0 to n − 1, we can get

(41)

Letting n → +∞, noting that V(n) → 0, we can get

(42)

associated with (36), and we have J ≤ μ₂∥ϕ∥² = J^*.

Remark 6. When time-delay in state vector keeps consistent with the delay in nonlinear perturbations and uncertain items disappear, the system (1) induced to

(43)

at the same time, the closed-loop system (7), and cost function (6) are reduced to

(44)

Then we give a sufficient condition for the existence of static output feedback control for system (43).

Theorem 7. For a given scalar α > 0, the control u(k) = Ky(k) is a static output feedback guaranteed cost controller for system (43), if there exist symmetric positive definite matrices P, Q₁, R₁, and K, arbitrary matrix N, and scalars ε₁ ≥ 0, ε₂ ≥ 0, such that the following LMI holds:

(45)

where

(46)

and the guaranteed cost value is given by J^* = μ₂∥ϕ∥², where

Proof. The proof of Theorem 7 is similar to that of Theorem 5, which are omitted.

Remark 8. In this paper, we design the controller directly from the LMI without variable transformation [11] which reduces the amount of calculation. Moreover, based on Theorem 5, one can deduce the criteria for linear discrete-time systems with time-delay and nonlinear discrete-time systems with constant time-delay.

4. Numerical Example

Consider the nonlinear uncertain discrete-time system (1) with the following parameters:

(47)

Given α = 0.032, d = 3, h = 2, β₁ = 0.23, β₂ = 0.25, and the initial condition

(48)

using the LMI Toolbox in MATLAB [14], the LMI (10) in Theorem 5 is satisfied with

(49)

and the controller parameter

(50)

Moveover, the solution of the closed-loop system satisfies

(51)

and the guaranteed cost of the closed-loop system is as follows

(52)

Simulation result is presented in Figure 1, which shows the convergence behavior of the proposed methods.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

State trajectories of the closed-loop system.

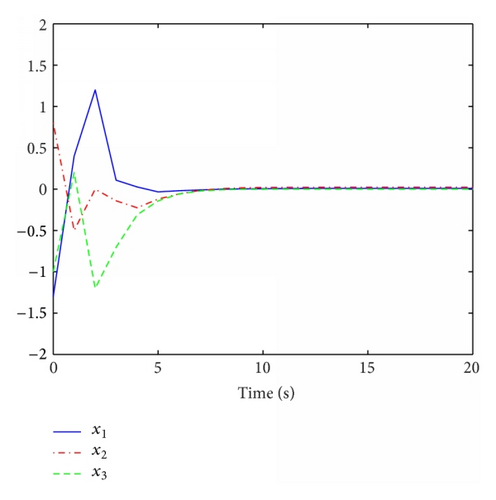
5. Conclusion

In this paper, the problem of robust output feedback guaranteed cost control for nonlinear uncertain disctere system is researched. For all admissible uncertainties, an output feedback guaranteed cost controller has been designed such that the resulting closed-loop system is robust exponentially stable and guarantees an adequate level of system performance. A numerical example has been presented to illustrate the efficiency of the result.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

References

1 Yaesh I. and Shaked U., H_∞ optimization with pole constraints of static output-feedback controllers-a non-smooth optimization approach, IEEE Transactions on Control Systems Technology. (2012) 20, no. 4, 1066–1072, https://doi.org/10.1109/TCST.2011.2158824, 2-s2.0-84861719730.
Google Scholar
2 Dong J. X. and Yang G. H., Static output feedback control synthesis for linear systems with time-invariant parametric uncertainties, IEEE Transactions on Automatic Control. (2007) 52, no. 10, 1930–1936, https://doi.org/10.1109/TAC.2007.906227, MR2355803, 2-s2.0-36249014749.
Google Scholar
3 Ho D. W. C. and Lu G., Robust stabilization for a class of discrete-time non-linear systems via output feedback: the unified LMI approach, International Journal of Control. (2003) 76, no. 2, 105–115, https://doi.org/10.1080/0020717031000067367, MR1965847, 2-s2.0-0037454724.
Google Scholar
4 Chang S. S. L. and Peng T., Adaptive guaranteed cost control of systems with uncertain parameters, IEEE Transactions on Automatic Control. (1972) 17, no. 4, 474–483, MR0449818, 2-s2.0-0015384273, https://doi.org/10.1109/TAC.1972.1100037.
Google Scholar
5 Dong J. X. and Yang G. H., Robust static output feedback control synthesis for linear continuous systems with polytopic uncertainties, Automatica. (2013) 49, no. 6, 1821–1829, https://doi.org/10.1016/j.automatica.2013.02.047, MR3049234, 2-s2.0-84877584286.
Google Scholar
6 Lien C. H., Non-fragile guaranteed cost control for uncertain neutral dynamic systems with time-varying delays in state and control input, Chaos, Solitons and Fractals. (2007) 31, no. 4, 889–899, https://doi.org/10.1016/j.chaos.2005.10.080, MR2262184, 2-s2.0-33747348121.
Google Scholar
7 Wei J., Dong Y., and Su Y., Guaranteed cost control of uncertain T-S fuzzy systems via output feedback approach, WSEAS Transactions on Systems. (2011) 10, no. 9, 306–317, 2-s2.0-80055008107.
Google Scholar
8 Chen W.-H., Guan Z.-H., and Lu X., Delay-dependent guaranteed cost control for uncertain discrete-time systems with delay, IEE Proceedings: Control Theory and Applications. (2003) 150, no. 4, 412–416, https://doi.org/10.1049/ip-cta:20030572, 2-s2.0-0141633842.
Google Scholar
9 Chen L., Unfragile guaranteed-cost H_∞ control of uncertain state-delay sampling system, Procedia Engineering. (2012) 29, 3359–3363.
Google Scholar
10 Qiu F., Cui B., and Ji Y., Further results on robust stability of neutral system with mixed time-varying delays and nonlinear perturbations, Nonlinear Analysis. Real World Applications. (2010) 11, no. 2, 895–906, https://doi.org/10.1016/j.nonrwa.2009.01.032, MR2571262, 2-s2.0-70449623984.
Web of Science® Google Scholar
11 Thuan M. V., Phat V. N., and Trinh H. M., Dynamic output feedback guaranteed cost control for linear systems with interval time-varying delays in states and outputs, Applied Mathematics and Computation. (2012) 218, no. 21, 10697–10707, https://doi.org/10.1016/j.amc.2012.04.039, MR2927085, 2-s2.0-84861799162.
Google Scholar
12 Park J. H., On dynamic output feedback guaranteed cost control of uncertain discrete-delay systems: LMI optimization approach, Journal of Optimization Theory and Applications. (2004) 121, no. 1, 147–162, https://doi.org/10.1023/B:JOTA.0000026135.99294.32, MR2062974, 2-s2.0-4043097506.
Google Scholar
13 Boyd S., El Ghaoui L., Feron E., and Balakrishan V., Linear Matrix Inequalities in System and Control Theory, 1994, 15, SIAM, Philadelphia, Pa, USA, https://doi.org/10.1137/1.9781611970777, MR1284712.
Google Scholar
14 Gahinet P., Nemirovskii A., Laub A. J., and Chilali M., LMI Control Toolbox: for Use with MATLAB, 1995, MathWorks, Inc., Natick, Mass, USA.
Google Scholar

All articles

Design of Robust Output Feedback Guaranteed Cost Control for a Class of Nonlinear Discrete-Time Systems

Abstract

1. Introduction

2. Preliminaries

3. Main Results

4. Numerical Example

5. Conclusion

Conflict of Interests

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Design of Robust Output Feedback Guaranteed Cost Control for a Class of Nonlinear Discrete-Time Systems

Abstract

1. Introduction

2. Preliminaries

3. Main Results

4. Numerical Example

5. Conclusion

Conflict of Interests

References

Figures

References

Related

Information