Volume 2014, Issue 1 627060

Research Article

Open Access

Pinning Synchronization of One-Sided Lipschitz Complex Networks

Fang Liu,

Fang Liu

orcid.org/0000-0002-0430-4381

School of Information Engineering, Huanghuai University, Henan 463000, China huanghuai.edu.cn

Search for more papers by this author

Qiang Song,

Corresponding Author

Qiang Song

[email protected]

orcid.org/0000-0001-9635-1355

School of Information Engineering, Huanghuai University, Henan 463000, China huanghuai.edu.cn

Search for more papers by this author

Jinde Cao,

Jinde Cao

orcid.org/0000-0003-3133-7119

Department of Mathematics, Southeast University, Nanjing 210096, China seu.edu.cn

Department of Mathematics, Faculty of Science, King Abdulaziz University, Jeddah 21589, Saudi Arabia kau.edu.sa

Search for more papers by this author

Jianquan Lu,

Jianquan Lu

orcid.org/0000-0003-4423-6034

Department of Mathematics, Southeast University, Nanjing 210096, China seu.edu.cn

Search for more papers by this author

Fang Liu,

Fang Liu

orcid.org/0000-0002-0430-4381

School of Information Engineering, Huanghuai University, Henan 463000, China huanghuai.edu.cn

Search for more papers by this author

Qiang Song,

Corresponding Author

Qiang Song

[email protected]

orcid.org/0000-0001-9635-1355

School of Information Engineering, Huanghuai University, Henan 463000, China huanghuai.edu.cn

Search for more papers by this author

Jinde Cao,

Jinde Cao

orcid.org/0000-0003-3133-7119

Department of Mathematics, Southeast University, Nanjing 210096, China seu.edu.cn

Department of Mathematics, Faculty of Science, King Abdulaziz University, Jeddah 21589, Saudi Arabia kau.edu.sa

Search for more papers by this author

Jianquan Lu,

Jianquan Lu

orcid.org/0000-0003-4423-6034

Department of Mathematics, Southeast University, Nanjing 210096, China seu.edu.cn

Search for more papers by this author

First published: 13 April 2014

https://doi.org/10.1155/2014/627060

Citations: 2

Academic Editor: Zhiqiang Zuo

Share a link

Email
Wechat
Bluesky

Abstract

This paper studies the pinning synchronization in complex networks with node dynamics satisfying the one-sided Lipschitz condition which is less conservative than the well-known Lipschitz condition. Based on M-matrix theory and Lyapunov functional method, some simple pinning conditions are derived for one-sided Lipschitz complex networks with full-state and partial-state coupling, respectively. A selective pinning scheme is further provided to address the selection of pinned nodes and the design of pinning feedback gains for one-sided Lipschitz complex networks with general topologies. Numerical results are given to illustrate the effectiveness of the theoretical analysis.

1. Introduction

A complex network is composed of a set of coupled dynamical systems where each system updates its state based on the local neighboring information such that the whole network might exhibit collective behaviors under some conditions. Nowadays, many natural and man-made systems in our daily life, such as biological networks, generic networks, electrical power grids, and the World Wide Web, can be described by complex networks.

The synchronization problem for complex networks has attracted much attention from various disciplines over the past decade [1, 2]. By proposing the master stability function, Pecora and Carroll [3] developed a unified approach to study the local synchronization in a network of dynamical systems. Wu [4] showed that the synchronization in a complex network with a sufficiently large coupling strength can always be reached if the interaction digraph of the network contains a directed spanning tree. Lu and Chen [5] presented a systematic framework to investigate the synchronization in linearly coupled complex networks with general topologies. Gómez-Gardeñes et al. [6] deeply studied the effects of coupling strength and network topology on the synchronizability of complex networks.

The synchronization of complex networks is usually achieved by using full-state variables of network nodes which may not always be available in practice. To resolve this difficulty, some control algorithms have been proposed to synchronize complex networks by utilizing the observed states of network nodes. Based on the state observer approach, Jiang et al. [7] formulated a complex network model and then derived some criteria to discuss the local synchronization in the network. Wu and Jiao [8] extended the work of Jiang et al. [7] to address the synchronization in complex networks with asymmetric coupling.

If a complex network cannot achieve synchronization by itself, one can design some appropriate controllers to force the network to synchronize onto a homogenous trajectory. However, for a network consisting of a large number of nodes, the control cost will be very high when the control actions are applied to all network nodes. Fortunately, one can adopt the pinning control strategy [9–20] to achieve synchronization in complex networks by placing control injections onto a subset of network nodes. Current studies have shown that an undirected complex network can be synchronized to some desired state by specifically or randomly pinning some nodes [9–12]. However, due to asymmetric coupling, the pinning control problem of a directed network is much more difficult than that of an undirected network. In recent years, some progress has been made in the pinning synchronization of directed networks. Chen et al. [13] and Lu et al. [14] have shown that a directed network can be pinned to the isolated node by using a minimum number of controllers, even a single controller. More recently, some researchers [18–20] proposed some techniques based on M-matrix theory [21] to study the pinning control problem for networked systems.

It is well-known that each node in complex networks is usually described by a nonlinear dynamical system. In most existing results on pinning control of complex networks, the node dynamics is assumed to satisfy the QUAD condition [12, 13, 15, 18]. Some authors considered the pinning control of complex networks with node dynamics satisfying Lipschitz condition [11, 14] and sector-restriction condition [22, 23]. In this paper, we further consider the pinning synchronization of complex networks composed of a set of nonlinear dynamical systems satisfying the one-sided Lipschitz condition [24–26] which is less conservative than the classical Lipschitz condition.

The main contribution of this paper is threefold. First, the paper studies the pinning control problem for both full-state and partial-state coupled complex networks with one-sided Lipschitz-type node dynamics. To the best of our knowledge, the synchronization in one-sided Lipschitz complex networks has not been addressed up to date. Therefore, the pinning control results for one-sided Lipschitz complex networks in this paper fill in this gap in time. Second, by using the properties of M-matrices, some simple pinning conditions in terms of low-dimensional linear matrix inequalities (LMIs) are established for both full-state and partial-state coupled complex networks. With the derived stability criteria, the pinning control problem of a large-scale network can be reduced to the test of a linear matrix inequality whose dimension is the same as that of a single network node. Third, we discuss the selection of pinned nodes and the design of pinning feedback gains for one-sided Lipschitz complex networks with both directed and undirected topologies based on M-matrix and algebraic graph theories.

The rest of this paper is organized as follows. In Section 2, some mathematical preliminaries are provided. Section 3 formulates the pinning control problem for complex networks with one-sided Lipschitz-type node dynamics. Sections 4 and 5 present some easily verified conditions for reaching pinning control in complex networks with full-state and partial-state coupling, respectively. Section 6 proposes a selective pinning scheme to satisfy the derived pinning conditions. In Section 7, numerical results are given to validate the theoretical analysis. Finally, some concluding remarks are stated in Section 8.

2. Preliminaries

This section provides some mathematical preliminaries to derive the main results of this paper.

2.1. Notations

The notations in this paper are quite standard. Let ℝ and ℂ represent the real number and complex number sets, respectively. Denote Re(z) as the real part of a complex number z ∈ ℂ. Let I_N be the N-dimensional identity matrix and let 1_n ∈ ℝⁿ be the vector of all ones. For a square matrix A ∈ ℝ^n×n, let A_s = (A + A^T)/2 and 𝒥(A) = min⁡_1≤i≤nRe(λ_i(A)) with λ_i(A) being the ith eigenvalue. For a symmetric real matrix X, let λ_min⁡(X) and λ_max⁡(X) be its minimum and maximum eigenvalues, respectively, and write X > 0 (X ≥ 0) if X is positive definite (positive semidefinite). For a vector x ∈ ℝⁿ, let ∥x∥ be its Euclidean norm. Given two matrices A and B, denote A ⊗ B as their Kronecker product [21].

2.2. One-Sided Lipschitz Dynamical System

A nonlinear dynamical system which does not satisfy Lipschitz condition may satisfy the so-called one-sided Lipschitz condition [24, 25].

Definition 1 (see [24].)A nonlinear function f(t, x) is said to satisfy one-sided Lipschitz condition if there exist a positive definite matrix P and a constant γ ∈ ℝ such that 〈P(f(t, x) − f(t, z)), x − z〉 ≤ γ∥x−z∥² holds for any x, z ∈ ℝⁿ, where 〈·, ·〉 denotes the inner product of two vectors.

Remark 2. The one-sided Lipschitz condition can be rewritten as (x−z)^TP(f(t, x) − f(t, z)) ≤ γ∥x−z∥². The constant γ is called the one-sided Lipschitz constant. It is worth mentioning that the one-sided Lipschitz constant can be any real number even a nonpositive number [24–26].

Remark 3. It is well-known that a nonlinear function f(t, x) is said to satisfy Lipschitz condition if there exists a positive number θ > 0 such that ∥f(t, x) − f(t, z)∥ ≤ θ∥x − z∥ holds for all x, z ∈ ℝⁿ. Therefore, one can easily obtain the Lipschitz constant θ by some simple calculations. However, for a one-sided Lipschitz function, it is quite challenging to find the one-sided Lipschitz constant γ because one has to design an appropriate structure for the matrix P in advance. In Section 7, some detailed examples are given to discuss the determination of the one-sided Lipschitz constant.

Remark 4. From Definition 1 and Remark 3, one can see that a one-sided Lipschitz function automatically satisfies Lipschitz condition, but the converse may be not true.

2.3. M-Matrix Theory

Some properties of M-matrices are important to study the pinning control of complex networks.

Lemma 5 (see [21].)For a nonsingular matrix A = (a_ij) _N×N ∈ ℝ^N×N with a_ij ≤ 0 (i ≠ j), the following statements are equivalent:

(1)
A is an M-matrix;
(2)
all entries of A⁻¹ are nonnegative;
(3)
all eigenvalues of A have positive real parts; that is, Re(λ_i(A)) > 0 for all i = 1, …, N;
(4)
there exists a positive definite diagonal matrix Ξ = diag⁡(ξ₁, …, ξ_N) > 0 such that ΞA + A^TΞ > 0.

3. Model Description and Problem Formulation

Consider a complex network composed of N identical coupled nodes, in which each node is a nonlinear dynamical system including linear and nonlinear terms:

()

where

is the state variable of the ith node, A ∈ ℝ^n×n, f(t, x_i(t)) ∈ ℝⁿ is a vector-valued function, σ > 0 is the coupling strength, l_ij is the (i, j)th entry of Laplacian matrix L ∈ ℝ^N×N defined as l_ij < 0 if there is a directed link from node j to node i (i ≠ j) and l_ij = 0, otherwise,

, Γ ∈ ℝ^n×n is the inner coupling matrix, and u_i is the control input for node i.

The leader node (or isolated node) for complex network (1) is given by

()

where

For complex network (1), let 𝒱 = {1, …, N} denote the set of all network nodes, where each node can only access the information of its neighbors. For the isolated node (2) which is not affected by any other node, we call its neighbors pinned nodes and let 𝒱_pin = {i₁, …, i_l} ⊂ 𝒱 denote the set of pinned nodes, where 1 ≤ l < N. Consider the following pinning control algorithm for complex network (1):

()

where the pinning feedback gains are defined as follows:

()

The node dynamics of complex network (1) is assumed to satisfy the one-sided Lipschitz condition.

Assumption 6. Suppose that a positive definite matrix P and a constant γ can be found such that the nonlinear function f in complex network (1) satisfies one-sided Lipschitz condition; that is,

()

4. Pinning Criteria for Network with Full-State Coupling

In this section, we consider the synchronization in complex network (3) with full-state coupling and derive some simple conditions for reaching pinning synchronization in the network.

Letting Γ = I_n in complex network (3), we have the following pinning-controlled network:

()

Remark 7. We see that complex network (6) is full-state coupled with all state variables of network nodes being used to achieve pinning synchronization.

Let e_i(t) = x_i(t) − x₀(t), i = 1, …, N. From (2) and (6), we obtain the following error system:

()

Denote

, and

. Rewrite (7) in the matrix form as

()

where D = diag⁡(d₁, …, d_N).

Based on M-matrix and algebraic graph theories, Song et al. [18, 19] showed that the quantity 𝒥(L + D) = min⁡_1≤i≤NRe(λ_i(L + D)) plays a fundamental role in analyzing the pinning control of networked systems. Now, we develop some pinning criteria for complex network (6).

Theorem 8. Suppose that there exists a positive definite matrix P such that Assumption 6 holds and the following condition is satisfied:

()

where γ is the one-sided Lipschitz constant and α is a positive constant subject to

()

where 𝒥(L + D) = min⁡_1≤i≤NRe(λ_i(L + D)) > 0.

Then, the pinning-controlled network (6) globally asymptotically synchronizes to leader node (2); that is, x_i(t) → x₀(t), i = 1, …, N, as t → ∞, for any initial condition.

Proof. Let λ_i be the ith eigenvalue of L + D. It is easy to verify that σλ_i − α is the ith eigenvalue of σ(L + D) − αI_N. It follows from condition (10) that Re(σλ_i − α) > 0 holds for all i = 1, …, N. Then, by the definition of L and Lemma 5, we know that σ(L + D) − αI_N is an M-matrix and there exists a positive definite diagonal matrix Ξ = diag⁡(ξ₁, …, ξ_N) > 0 such that

()

Construct the following Lyapunov function candidate:

()

where P satisfies LMI condition (9).

By Assumption 6 and the properties of Kronecker product [21], the time derivative of V(t) along the trajectory of error system (8) yields

()

It follows from (9), (11), and (13) that holds for all e ≠ 0_Nn. Hence, the error system (8) is globally asymptotically stable at the origin. Then, complex network (6) globally asymptotically synchronizes to leader node (2).

Remark 9. From condition (10), we see that the quantity 𝒥(L + D) = min⁡_1≤i≤NRe(λ_i(L + D)) is important to study the pinning synchronization in network (6). To ensure 𝒥(L + D) > 0, Song et al. [18, 19] have shown that the leader node should have a directed path to every other network node. Section 6 will provide more details to discuss the selection of pinned nodes and the design of pinning feedback gains.

Remark 10. Note that the dimension of LMI (9) is the same as that of a single network node. By choosing the constant α according to condition (10), one can solve LMI (9) to find feasible solution of P by using some toolboxes such as YALMIP [27].

In Theorem 8, the interaction digraph 𝒢 of complex network is assumed to be general. When 𝒢 is undirected, it is easy to obtain L = L^T and one has the following result from Theorem 8.

Corollary 11. Assume that L is symmetric. There exists a positive definite matrix P such that Assumption 6 holds and

()

where λ₁ = λ_min⁡(L + D) > 0. Then, complex network (6) globally asymptotically synchronizes to leader node (2).

Proof. Obviously, L + D is symmetric with all eigenvalues being real numbers when L = L^T. By Lemma 5, we know that matrix L + D is positive definite if λ_min⁡(L + D) > 0.

Take the Lyapunov function candidate as follows:

()

where P satisfies LMI condition (14).

In view of the proof of Theorem 8, the time derivative of V(t) along the trajectory of error system (8) satisfies

()

where the second inequality is obtained by using L + D ≥ λ₁I_N.

From (14) and (16), we can show that the pinning-controlled complex network (6) globally asymptotically synchronizes to leader node (2) by using Lyapunov stability theory.

Remark 12. When L = L^T, the topology of network (3) is undirected. Then, the pinned nodes can be randomly or specifically chosen, and one can first pin the most highly connected nodes to achieve larger λ_min⁡(L + D) [9, 10].

5. Pinning Criteria for Network with Partial-State Coupling

In the previous section, complex network (6) is a full-state coupled network. However, in many practical cases, the full states of network nodes may not always be available. By utilizing the output states of network nodes, this section derives some pinning criteria for partial-state coupled complex networks.

For complex network (3), assume that a matrix C ∈ ℝ^m×n (m < n) can be freely chosen such that the matrix pair (A, C) is detectable. For complex network (3), let Γ = P⁻¹C^TC, where P ∈ ℝ^n×n is a positive definite matrix to be designed. Consider the following pinning-controlled network:

()

Remark 13. Let y_i(t) = Cx_i(t), i = 0, …, N, be the output states of network nodes and let F = P⁻¹C^T ∈ ℝ^n×m be the output-feedback gain matrix such that A − FC is Hurwitz. Then, complex network (17) can be rewritten as

()

Note that the output states are actually adopted to reach pinning synchronization in complex network (17), which means that network (17) is partial-state coupled rather than full-state coupled.

Remark 14. If the matrix pair (A, C) is detectable, one can always find a matrix F ∈ ℝ^n×m to ensure that A − FC is Hurwitz. Moreover, there always exist a positive definite matrix P and a scalar τ > 0 such that PA + A^TP − τC^TC < 0 [28].

Theorem 15. Suppose that there exists a positive definite matrix P such that Assumption 6 and the following condition hold:

()

where β is a positive constant satisfying

()

Then, the pinning-controlled network (17) globally asymptotically synchronizes to leader node (2).

Proof. Following the similar line in the proof of Theorem 8, from condition (20), we can show that σ(L + D) − βI_N is an M-matrix and there exists a positive definite diagonal matrix Ξ = diag⁡(ξ₁, …, ξ_N) > 0 such that

()

From (2) and (17), we obtain the following error system:

()

Consider the following Lyapunov function candidate:

()

where P satisfies Assumption 6 and condition (19).

Calculate the time derivative of V(t) along the trajectory of the error system (22) as follows:

()

Obviously, C^TC is positive semidefinite; that is, C^TC ≥ 0. Then, it follows from (19), (21), and (24) that holds for all e ≠ 0_Nn. Hence, error system (22) is globally asymptotically stable at the origin, which indicates that network (17) globally asymptotically synchronizes to leader node (2).

Remark 16. Note that the dimension of LMI (19) is the same as that of a single network node.

Remark 17. In Remark 14, we have pointed out that one can always find a positive definite matrix P ∈ ℝ^n×n and a scalar τ > 0 such that PA + A^TP − τC^TC < 0 if the matrix pair (A, C) is detectable. To utilize this important result related to system detectability, we intentionally introduce the parameter β in Theorem 15 as a transitional variable to derive condition (19). Treating β as a scalar matrix, we can solve LMIs (19) and (20) to obtain appropriate parameters β and P.

Corollary 18. Suppose that Assumption 6 holds and L is symmetric. There exists a positive definite matrix P such that

()

where λ₁ = λ_min⁡(L + D) > 0. Then, the complex network (17) globally asymptotically synchronizes to leader node (2).

Proof. Take the following Lyapunov function candidate as

()

where P satisfies LMI condition (25).

Then, the time derivative of V(t) along the trajectory of the error system (22) is obtained as follows:

()

By (25) and (27), we can show that complex network (17) globally asymptotically synchronizes to leader node (2).

6. Selective Pinning Scheme

In this section, we discuss the selection of pinned nodes and the design of pinning feedback gains. A selective pinning scheme for complex networks with general topologies is proposed to satisfy the pinning conditions in Theorems 8 and 15.

For complex network (1), let 𝒢 denote the interaction graph of the network and suppose that p is the multiplicity of the zero eigenvalue of the Laplacian matrix L. Song et al. [18, 19] showed that the digraph of the network can be partitioned into p components with each component having a directed tree. To ensure that 𝒥(L + D) > 0 holds, at least one root node in each component should be pinned such that the leader node (2) has a directed path to every other network node. Moreover, Song et al. [19] have shown that 𝒥(L + D) monotonically increases with respect to the number of pinned nodes or pinning feedback gains. However, 𝒥(L + D) ≤ 𝒥(L(𝒱∖𝒱_pin)) always holds even if the pinning feedback gains are sufficiently large. Therefore, it is better to take relatively lower pinning feedback gains. For directed complex networks, Song and Cao [15] pointed out that the nodes whose out-degrees are bigger than their in-degrees should be chosen as pinned candidates.

Now, we present the following selective pinning scheme for complex network (1) such that the conditions in Theorem 8 (or Theorem 15) can be satisfied for reaching pinning synchronization.

(1)
Partition the digraph 𝒢 of complex network (1) into p components where each component contains a directed tree. Initialize 𝒱_pin with p root nodes of these components.
(2)
Rearrange the remaining N − p nodes in descending order according to the differences of their out-degrees and in-degrees and choose appropriate pinning feedback gains.
(3)
Solve LMI (9) (or LMIs (19) and (20)). If no feasible solution is found, continually add more network nodes to 𝒱_pin or increase pinning feedback gains until the conditions in Theorem 8 (or Theorem 15) are satisfied.

7. Numerical Examples

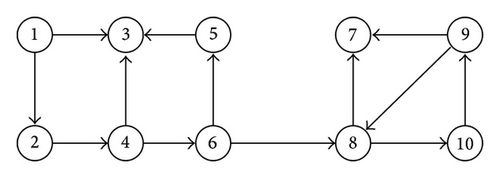
In this section, some numerical results are provided to illustrate the effectiveness of our theoretical analysis. A digraph with ten nodes is shown in Figure 1, in which the element of the Laplacian matrix L is taken as l_ij = −1 if there is a directed link from node j to node i.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

A digraph with ten nodes.

Note that the digraph in Figure 1 has a directed tree with node 1 being the unique root. According to the selective pinning scheme in Section 6, node 1 should be pinned. Let σ = 10 be the coupling strength and let d = 5 be the pinning feedback gain. If node 1 is pinned, we have

()

Consider a complex network with one-sided Lipschitz-type node dynamics in the form of (1) where

()

and the nonlinear function is given by

()

It is not difficult to check that f(t, x_i) is not a Lipschitz-type function. Now, we use some techniques in [25] to show that f(t, x_i) satisfies one-sided Lipschitz condition. For any

, and

, applying the well-known mean-value theorem yields [25]

()

where ς ∈ (min⁡{x_i4, s₄}, max⁡{x_i4, s₄}). Hence, f is a one-sided Lipschitz function with γ = 0.

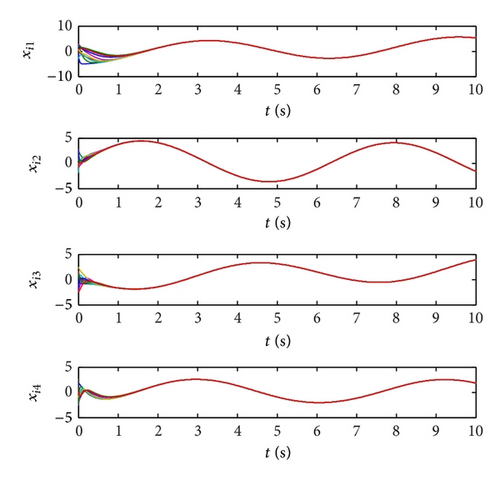
Case 1 (full-state coupling). Taking α = 0.75, we solve LMI (9) by using YALMIP toolbox and obtain

()

Applying pinning control action to node 1 with algorithm (6), we depict the time variations of network states in Figure 2. Note that the network is successfully pinned to a homogenous state.

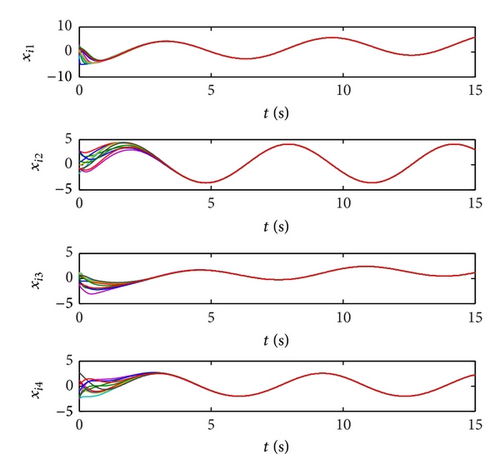
Case 2 (partial-state coupling). Choosing , it is easy to verify that the matrix pair (A, C) is detectable. The following parameters are obtained to satisfy conditions (19) and (20) of Theorem 15:

()

Using algorithm (17), we apply pinning control to the network by utilizing the output states of the network. The time variations of network states are shown in Figure 3, from which it is easy to see that the network achieves pinning synchronization.

8. Conclusions

In this paper, the pinning synchronization problem for one-sided Lipschitz complex networks has been investigated by using M-matrix and algebraic graph theories. Some simple pinning criteria in terms of low-dimensional linear matrix inequalities have been established for full-state and partial-state coupled complex networks, respectively. In particular, the output states of network nodes are utilized to implement the distributed pinning control algorithm. A selective pinning scheme has been proposed to satisfy the derived pinning conditions for one-sided Lipschitz complex networks with general topologies. In the near future, it would be of interest to study the pinning control problem for one-sided Lipschitz-type complex networks with dynamically switching topologies and time delays.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

This work was jointly supported by the National Science Foundation of China under Grants 61273218, 61304172, 61272530, and 61175119 and the Natural Science Foundation of Henan Province of China under Grants 122102210027, 122300410220 and 12B480005.

References

1 Wu C. W., Synchronization in Complex Networks of Nonlinear Dynamical Systems, 2007, World Scientific, Singapore.
10.1142/6570
Google Scholar
2 Arenas A., Díaz-Guilera A., Kurths J., Moreno Y., and Zhou C., Synchronization in complex networks, Physics Reports. (2008) 469, no. 3, 93–153, https://doi.org/10.1016/j.physrep.2008.09.002, MR2477097.
10.1016/j.physrep.2008.09.002
Web of Science® Google Scholar
3 Pecora L. M. and Carroll T. L., Master stability functions for synchronized coupled systems, Physical Review Letters. (1998) 80, no. 10, 2109–2112, 2-s2.0-4243241129.
10.1103/PhysRevLett.80.2109
CAS Web of Science® Google Scholar
4 Wu C. W., Synchronization in networks of nonlinear dynamical systems coupled via a directed graph, Nonlinearity. (2005) 18, no. 3, 1057–1064, https://doi.org/10.1088/0951-7715/18/3/007, MR2134084, ZBL1089.37024.
10.1088/0951-7715/18/3/007
PubMed Web of Science® Google Scholar
5 Lu W. and Chen T., New approach to synchronization analysis of linearly coupled ordinary differential systems, Physica D. Nonlinear Phenomena. (2006) 213, no. 2, 214–230, https://doi.org/10.1016/j.physd.2005.11.009, MR2201200, ZBL1105.34031.
10.1016/j.physd.2005.11.009
Web of Science® Google Scholar
6 Gómez-Gardeñes J., Moreno Y., and Arenas A., Synchronizability determined by coupling strengths and topology on complex networks, Physical Review E. Statistical, Nonlinear, and Soft Matter Physics. (2007) 75, no. 6, 11, 066106, https://doi.org/10.1103/PhysRevE.75.066106, MR2362021.
10.1103/PhysRevE.75.066106
CAS PubMed Web of Science® Google Scholar
7 Jiang G.-P., Tang W. K.-S., and Chen G., A state-observer-based approach for synchronization in complex dynamical networks, IEEE Transactions on Circuits and Systems. I. Regular Papers. (2006) 53, no. 12, 2739–2745, https://doi.org/10.1109/TCSI.2006.883876, MR2370459.
10.1109/TCSI.2006.883876
Web of Science® Google Scholar
8 Wu J. and Jiao L., Observer-based synchronization in complex dynamical networks with nonsymmetric coupling, Physica A. Statistical Mechanics and Its Applications. (2007) 386, 469–480.
10.1016/j.physa.2007.06.046
Web of Science® Google Scholar
9 Wang X. F. and Chen G., Pinning control of scale-free dynamical networks, Physica A. Statistical Mechanics and Its Applications. (2002) 310, no. 3-4, 521–531, https://doi.org/10.1016/S0378-4371(02)00772-0, MR1946327, ZBL0995.90008.
10.1016/S0378-4371(02)00772-0
Web of Science® Google Scholar
10 Li X., Wang X. F., and Chen G., Pinning a complex dynamical network to its equilibrium, IEEE Transactions on Circuits and Systems. I. Regular Papers. (2004) 51, no. 10, 2074–2087, https://doi.org/10.1109/TCSI.2004.835655, MR2096915.
10.1109/TCSI.2004.835655
Web of Science® Google Scholar
11 Porfiri M. and di Bernardo M., Criteria for global pinning-controllability of complex networks, Automatica. (2008) 44, no. 12, 3100–3106, https://doi.org/10.1016/j.automatica.2008.05.006, MR2531411, ZBL1153.93329.
10.1016/j.automatica.2008.05.006
Web of Science® Google Scholar
12 Yu W., Chen G., and Lü J., On pinning synchronization of complex dynamical networks, Automatica. (2009) 45, no. 2, 429–435, https://doi.org/10.1016/j.automatica.2008.07.016, MR2527339, ZBL1158.93308.
10.1016/j.automatica.2008.07.016
Web of Science® Google Scholar
13 Chen T., Liu X., and Lu W., Pinning complex networks by a single controller, IEEE Transactions on Circuits and Systems. I. Regular Papers. (2007) 54, no. 6, 1317–1326, https://doi.org/10.1109/TCSI.2007.895383, MR2370589.
10.1109/TCSI.2007.895383
Web of Science® Google Scholar
14 Lu J., Ho D. W. C., and Wang Z., Pinning stabilization of linearly coupled stochastic neural networks via minimum number of controllers, IEEE Transactions on Neural Networks. (2009) 20, no. 10, 1617–1629, 2-s2.0-70350347096, https://doi.org/10.1109/TNN.2009.2027810.
10.1109/TNN.2009.2027810
PubMed Web of Science® Google Scholar
15 Song Q. and Cao J., On pinning synchronization of directed and undirected complex dynamical networks, IEEE Transactions on Circuits and Systems. I. Regular Papers. (2010) 57, no. 3, 672–680, https://doi.org/10.1109/TCSI.2009.2024971, MR2729966.
10.1109/TCSI.2009.2024971
Web of Science® Google Scholar
16 Su H. S. and Wang X. F., Pinning Control of Complex Networked Systems: Synchronization, Consensus and Flocking of Networked Systems via Pinning, 2013, Springer, Shanghai Jiaotong University Press, https://doi.org/10.1007/978-3-642-34578-4, MR3014429.
10.1007/978-3-642-34578-4
Google Scholar
17 Su H. S., Rong Z., Chen M. Z. Q., Wang X. F., Chen G., and Wang H., Decentralized adaptive pinning control for cluster synchronization of complex dynamical networks, IEEE Transactions on Cybernetics. (2013) 43, no. 1, 394–399.
10.1109/TSMCB.2012.2202647
PubMed Web of Science® Google Scholar
18 Song Q., Liu F., Cao J., and Yu W., Pinning-controllability analysis of complex networks: an M-matrix approach, IEEE Transactions on Circuits and Systems. I. Regular Papers. (2012) 59, no. 11, 2692–2701, https://doi.org/10.1109/TCSI.2012.2190573, MR2996246.
10.1109/TCSI.2012.2190573
Web of Science® Google Scholar
19 Song Q., Liu F., Cao J., and Yu W., M-matrix strategies for pinning-controlled leader-following consensus in multiagent systems with nonlinear dynamics, IEEE Transactions on Cybernetics. (2013) 43, no. 6, 1688–1697.
10.1109/TSMCB.2012.2227723
PubMed Web of Science® Google Scholar
20 Wen G., Duan Z., Chen G., and Yu W., Consensus tracking of multi-agent systems with Lipschitz-type node dynamics and switching topologies, IEEE Transactions on Circuits and Systems. I: Regular Papers. (2014) 61, no. 2, 499–511.
10.1109/TCSI.2013.2268091
Web of Science® Google Scholar
21 Horn R. A. and Johnson C. R., Topics in Matrix Analysis, 1991, Cambridge University Press, Cambridge, UK, https://doi.org/10.1017/CBO9780511840371, MR1091716.
10.1017/CBO9780511840371
Google Scholar
22 Li Z., Duan Z., and Chen G., Global synchronised regions of linearly coupled Lur′e systems, International Journal of Control. (2011) 84, no. 2, 216–227, https://doi.org/10.1080/00207179.2010.546882, MR2783574, ZBL1222.93085.
10.1080/00207179.2010.546882
Web of Science® Google Scholar
23 Song Q., Liu F., Cao J., and Lu J., Some simple criteria for pinning a Lur′e network with directed topology, IET Control Theory and Applications. (2014) 8, no. 2, 131–138.
10.1049/iet-cta.2013.0422
Web of Science® Google Scholar
24 Hu G.-D., Observers for one-sided Lipschitz non-linear systems, IMA Journal of Mathematical Control and Information. (2006) 23, no. 4, 395–401, https://doi.org/10.1093/imamci/dni068, MR2271168.
10.1093/imamci/dni068
Web of Science® Google Scholar
25 Zhao Y., Tao J., and Shi N.-Z., A note on observer design for one-sided Lipschitz nonlinear systems, Systems & Control Letters. (2010) 59, no. 1, 66–71, https://doi.org/10.1016/j.sysconle.2009.11.009, MR2650441, ZBL1186.93017.
10.1016/j.sysconle.2009.11.009
Web of Science® Google Scholar
26 Zhang W., Su H.-S., Liang Y., and Han Z.-Z., Non-linear observer design for one-sided Lipschitz systems: an linear matrix inequality approach, IET Control Theory & Applications. (2012) 6, no. 9, 1297–1303, https://doi.org/10.1049/iet-cta.2011.0386, MR2986750.
10.1049/iet-cta.2011.0386
Web of Science® Google Scholar
27 Löfberg J., YALMIP: a toolbox for modeling and optimization in MATLAB, Proceedings of the IEEE International Symposium on Computer Aided Control System Design, September 2004, Taipei, Taiwan, 284–289, 2-s2.0-20344396845.
Google Scholar
28 Boyd S., El Ghaoui L., Feron E., and Balakrishnan V., Linear Matrix Inequalities in System and Control Theory, 1994, 15, Society for Industrial and Applied Mathematics (SIAM), Philadelphia, Pa, USA, SIAM Studies in Applied Mathematics, https://doi.org/10.1137/1.9781611970777, MR1284712.
10.1137/1.9781611970777
Google Scholar

Citing Literature

All articles

Pinning Synchronization of One-Sided Lipschitz Complex Networks

Abstract

1. Introduction

2. Preliminaries

2.1. Notations

2.2. One-Sided Lipschitz Dynamical System

2.3. M-Matrix Theory

3. Model Description and Problem Formulation

4. Pinning Criteria for Network with Full-State Coupling

5. Pinning Criteria for Network with Partial-State Coupling

6. Selective Pinning Scheme

7. Numerical Examples

8. Conclusions

Conflict of Interests

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Pinning Synchronization of One-Sided Lipschitz Complex Networks

Abstract

1. Introduction

2. Preliminaries

2.1. Notations

2.2. One-Sided Lipschitz Dynamical System

2.3. M-Matrix Theory

3. Model Description and Problem Formulation

4. Pinning Criteria for Network with Full-State Coupling

5. Pinning Criteria for Network with Partial-State Coupling

6. Selective Pinning Scheme

7. Numerical Examples

8. Conclusions

Conflict of Interests

Acknowledgments

References

Citing Literature

Figures

References

Related

Information