Design strategies for parallel iterative algorithms are presented. In order to further study different tradeoff strategies in design criteria for integrated circuits, A 10 × 10 Jacobi Brent-Luk-EVD array with the simplified μ-CORDIC processor is used as an example. The experimental results show that using the μ-CORDIC processor is beneficial for the design criteria as it yields a smaller area, faster overall computation time, and less energy consumption than the regular CORDIC processor. It is worth to notice that the proposed parallel EVD method can be applied to real-time and low-power array signal processing algorithms performing beamforming or DOA estimation.

1. Introduction

We are on the edge of many important developments which will require parallel data and information processing. The transmission systems are using higher and higher frequencies and the carrier frequencies are increasing to 10 GHz and above. Because of the smaller wavelength more antennas can be implemented on a single device leading to massive MIMO systems. Parallel VLSI architectures will be needed in order to provide the required computational power for 10 GHz and above, massive MIMO, and big data processing [1, 2].

In parallel matrix computation at the circuit level, implementing an iterative algorithm on a multiprocessor array results in a tradeoff between the complexity of an iteration step and the number of required iteration steps. Therefore, as long as the algorithm′s convergence properties are guaranteed, it is possible to adjust the architecture, which can significantly reduce the complexity with regard to the implementation. Computing the parallel eigenvalue decomposition (EVD) as a preprocessing step to MUSIC or ESPRIT algorithm with Jacobi′s iterative method is used as an important example as the convergence of this method is extremely robust to modifications of the processor elements [3–6].

In [7], it was shown that Brent-Luk-EVD architecture with a modified CORDIC for performing the plane rotation of the Jacobi algorithm can be realized in advanced VLSI design. Based on it, a Jacobi EVD array is realized by implementing a scaling-free microrotation CORDIC (μ-CORDIC) processor in this paper, which only performs a predefined number of CORDIC iterations. Therefore, the size of the processor array can be reduced for implementing a large-scale EVD array in parallel VLSI architectures. After that, several modifications of the algorithm/processor are studied and their impact on the design criteria is investigated for different sizes of EVD array (10 × 10 to 80 × 80). Finally, a strategy to comply with the design criteria is established, especially in terms of balancing the number of microiterations and the computational complexity. The proposed architecture is ideal for real-time antenna array applications, such as a flying object carrying an antenna array for beamforming or DOA estimation that would require a real-time, low-power, and efficient architecture for EVD, or joint time-delay and frequency estimation using a sensor network.

This paper is organized as follows. Serial and parallel Jacobi methods are described in Section 2. In Section 3, the design issues of the parallel Jacobi EVD array are discussed, leading to the simplification from a regular full CORDIC to the μ-CORDIC processor with an adaptive number of iterations. Section 4 shows the implementation results. Section 5 concludes this paper.

2. Parallel Eigenvalue Decomposition

2.1. Jacobi Method

An eigenvalue decomposition of a real symmetric n × n matrix A is obtained by factorizing A into three matrices A = Q∧Q^T, where Q is an orthogonal matrix (QQ^T = I) and ∧ is a diagonal matrix containing the eigenvalues of A. The Jacobi method approximates the EVD iteratively as follows:

()

where Q_k is an orthonormal plane rotation by the angle θ in the (i, j) plane.

The plane rotations Q_k, where k = 1,2, 3, …, can be executed in various orders to obtain the eigenvalues. The most common order of sequential plane rotations {Q_k} is called cyclic-by-row, meaning (i, j) is chosen as follows:

()

The execution of all N = n(n − 1)/2 index pairs (i, j) is called a sweep. Matrix A will converge into a diagonal matrix ∧ once k sweeps are applied, where ∧ contains the eigenvalues λ₁, λ₂, …, λ_n:

()

2.2. Jacobi EVD Array

Instead of performing the plane rotations Q_k one by one in a cyclic-by-row order, they can be separated into multiple subproblems and executed in parallel on a log n dimensional multicore platform. Ahmedsaid et al. [3] first presented a parallel array based on Jacobi’s method. It consists of n/2 × n/2 PEs and each PE contains a 2 × 2 subblock of the matrix A. Figure 1 shows a typical 4 × 4 EVD array with 16 PEs. This Jacobi array can perform n/2 subproblems in parallel. Initially, each PE holds a 2 × 2 submatrix of A:

()

where p and q = 1,2, …, n/2.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

A 4 × 4 Brent-Luk-EVD array, where n = 8 for an 8 × 8 symmetric matrix [3].

A rotation angle has to be chosen in order to zero out the off-diagonal elements of the submatrix by solving a 2 × 2 symmetric EVD subproblem as shown in the following:

()

where

The maximal reduction

can be obtained by applying the optimal angle of rotation θ_opt:

()

where the range of θ_opt is limited to |θ_opt| ≤ π/4.

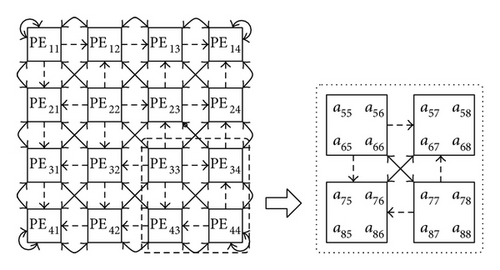
This optimal angle θ_opt, which can annihilate the off-diagonal elements (a_2p−1,2q and a_2p,2q−1), is computed using diagonal PEs in (6). Once these rotation angles are computed, they will be sent to the off-diagonal PEs. This transmission is indicated by the dashed lines in the vertical and horizontal direction in Figure 1. All off-diagonal PEs will perform a two-sided rotation with the corresponding rotation angles obtained from the row (θ_r) and column (θ_c), respectively.

Once these rotations are applied, the matrix elements are interchanged between processors as indicated by the diagonal solid lines in Figure 1, for the execution of the next n/2 rotations. One sweep needs to perform n − 1 of these parallel rotation steps. After several sweeps (iterations) are executed, the eigenvalues will concentrate in the diagonal PEs.

3. CORDIC Approach

3.1. Regular CORDIC

Within each PE, a simple way to solve the subproblem of (5) in VLSI for zeroing out the off-diagonal elements is to use the CORDIC algorithm. An orthogonal CORDIC rotator is defined as [8, 9]

()

when n → ∞, A_n≅1.647.

In the Cartesian coordinate system, the CORDIC orthogonal rotation mode can be used to compute (5) by separating the two-sided rotation into two parts,

and R · G. A · R^T that is computed by

()

where the plane rotation with the desired rotation angle θ_opt is executed using two CORDIC rotators. The CORDIC processors apply n steps, usually n = 32 for single floating precision. A constant scaling value K = 1/A_n = 0.6073 is subsequently required to fix the rotated vectors

and

in order to retain the orthonormality. Similarly, these two CORDIC rotators can also be applied to compute R · G:

()

Meanwhile, the angle θ_opt can also be determined by using the CORDIC orthogonal vector mode. The CORDIC rotates the input vector through whatever angle is necessary to align the resulting vector with the x-axis:

()

The CORDIC with an orthogonal vector mode can compute the arctangent result iteratively θ = arctan(y/x), if the angle accumulator is initialized with zero (z₀ = 0).

In the VLSI design, two common approaches can be used to realize the CORDIC dependence flow graph in hardware: the folded (serial) or the parallel (pipelining) [10, 11]. Note that we limit our efforts to the conventional CORDIC iteration scheme, as given in (7). In Figure 2(a), the structure of a folded CORDIC PE is shown, which requires a pair of adders for plane rotation and another adder for steering the next angle direction (computing the following z_i and d_i). All internal variables are buffered in the registers separately until the iteration number is large enough to obtain the result. The signs of all three intermediate variables are fed into a control unit that generates the rotation direction flags d_i to steer the add or suboperations and keep track of the rotation angle z_i. For example, off-diagonal PE₄₃ can directly apply the flags d_i from PE₃₃ to (8)’s G₁ and PE₄₄ to (8)’s G₂. After the rotation, the required scaling procedure can be obtained using the part of Figure 2(b) that fixes A_n, where two multiplexers are required to select the inputs into the barrel shifters. This folded dependence graph is typical for the orthogonal rotation mode and benefits in a small area in the VLSI design.

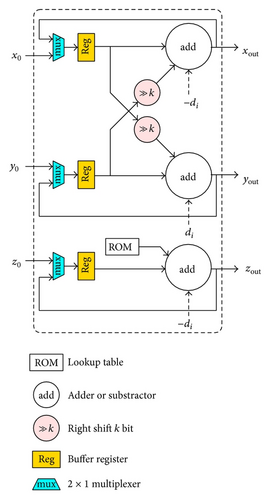
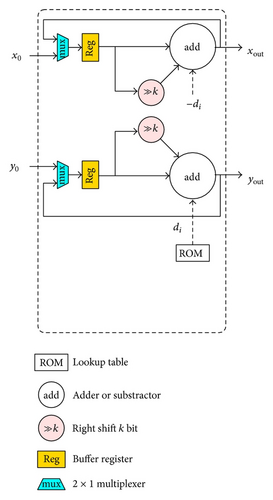
In practice, the angle accumulator is not required for the off-diagonal PEs. The d_i from (7) can be used to steer the rotators. Thus, the transmission on the vertical and horizontal dashed lines in Figure 1 will be replaced by a sequence of d_i flags, meaning that the off-diagonal computation efforts for computing the optimal angle θ_opt can be omitted.

3.2. Simplified μ-Rotation CORDIC

As the process technologies continue to shrink, it becomes possible to directly implement a Brent-Luk-EVD array with the Jacobi method [12, 13]. However, the size of the EVD array that can be implemented on the current configurable device with the regular CORDIC is still small, say, 4 × 4. Therefore, we must simplify the architecture in order to integrate more processors. A scaling-free μ-CORDIC for performing the plane rotation in (5) is used [5, 6], where the number of inner iterations is reduced from 32 iterations to only one iteration.

The definition of μ-CORDIC can be developed from (7) as

()

where

is the required scaling factor per iteration and ϵ is the scaling error. The idea of the μ-CORDIC rotation is to reduce the number of iterations of the full CORDIC to only a few iterations. Meanwhile, the scaling error ϵ will be small enough to be neglected as long as the orthonormality is retained. Figure 3 shows four different methods for different sizes of μ-rotation angles and Table 1 shows a lookup table for the μ-CORDIC, listing 32 approximated rotation angles for each μ-rotation type, the required number of shift-add operations and its computation cycles. Note that the approximated angles are stored as two times of tan⁡θ. When the rotation angle is very tiny (i.e., ϵ is tiny, too), Type I with only one iteration will comply with the limited working range

, if the selected n_m (n_m ∈ 1 ⋯ 32) is larger than 16. In Figure 3(a), a pair of shift-add operations realizing one iteration step is sufficient. Furthermore, it is scaling free when the angle 2 × tan⁡θ ≤ 3.05176 × 10⁻⁵. These orthonormal μ-rotations are chosen such that they satisfy a predefined accuracy condition in order to approximate the original rotation angles and are constructed by the least computation efforts.

Table 1. The lookup table for μ-rotations CORDIC with 32-bit accuracy, showing the rotation type, the 2 × tan⁡θ angle, the required shift-add operations for rotation and scaling, the required cycle delay, and repeat number for CORDIC-6.

Index	Type	Angle	Shift-add		Cycle
k	Type	2 × tan⁡θ	rot.	sca.	cnt.	re.
1	IV	1.49070	4	8	6	1
2	IV	0.54296	4	6	5	1
3	IV	0.25501	4	6	5	1
4	IV	0.12561	4	4	4	1

5	III	6.25841 10⁻²	6	0	3	2
6	III	3.12606 10⁻²	6	0	3	2
7	III	1.56263 10⁻²	6	0	3	2

8	II	7.81266 10⁻³	4	0	2	3
9	II	3.90627 10⁻³	4	0	2	3
10	II	1.95313 10⁻³	4	0	2	3
11	II	9.76563 10⁻⁴	4	0	2	3
12	II	4.88281 10⁻⁴	4	0	2	3
13	II	2.44141 10⁻⁴	4	0	2	3
14	II	1.22070 10⁻⁴	4	0	2	4
15	II	6.10352 10⁻⁵	4	0	2	5

16	I	3.05176 10⁻⁵	2	0	1	6
17	I	1.52588 10⁻⁵	2	0	1	6
18	I	7.62939 10⁻⁶	2	0	1	6
19	I	3.81470 10⁻⁶	2	0	1	6
20	I	1.90735 10⁻⁶	2	0	1	6
21	I	9.53674 10⁻⁷	2	0	1	6
22	I	4.76837 10⁻⁷	2	0	1	6
23	I	2.38419 10⁻⁷	2	0	1	6
24	I	1.19209 10⁻⁷	2	0	1	6
25	I	5.96046 10⁻⁸	2	0	1	6
26	I	2.98023 10⁻⁸	2	0	1	6
27	I	1.49012 10⁻⁸	2	0	1	6
28	I	7.45058 10⁻⁹	2	0	1	5
29	I	3.72529 10⁻⁹	2	0	1	4
30	I	1.86265 10⁻⁹	2	0	1	3
31	I	9.31323 10⁻¹⁰	2	0	1	2
32	I	4.65661 10⁻¹⁰	2	0	1	1

Next, for the Type II rotation (as shown in Figure 3(b)), when n_m is selected from 8 to 15 for small angles, two pairs of shift-add operations are enough to retain the orthonormality. Moreover, when the n_m is selected from 5 to 7, Type III requires three μ-rotations. No scaling is required by Types I through III. Finally, for large rotation angles, the scaling errors cannot be omitted. Figure 3(d) shows the corresponding dependence flow graph for Type IV. Besides the rotation itself, it requires two pairs of shift-add operations at the beginning of the flow graph, while 2 to 4 pairs of shift-add operations are required to fix the scaling factor

()

Note that the scaling costs M = 2 to 4 pairs of shift-add operations. In general, the cost of Type IV is bounded by 2 + M pairs of shift-add operations. For example, when the index k is 2, the scaling is

()

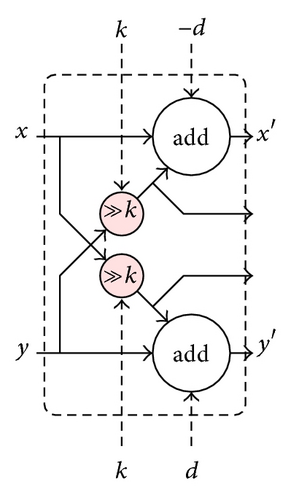
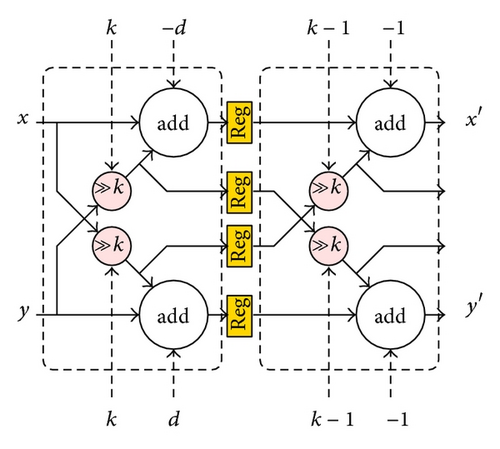
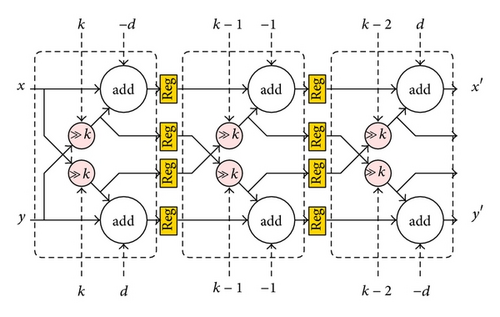
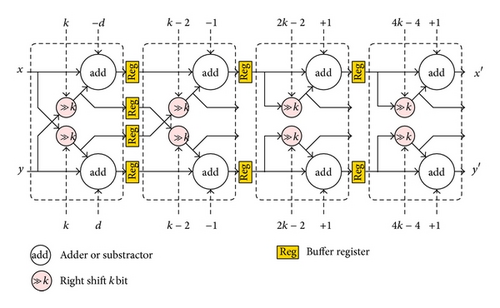
These four subtypes have three identical parts: Type I with one iteration, the scaling part of Type IV, and the second iteration of Type II. These three parts can be integrated together by using multiplexers to select the data paths, as shown in Figure 4, where 2 adders, 2 shifters, and 4 multiplexers are required [5].

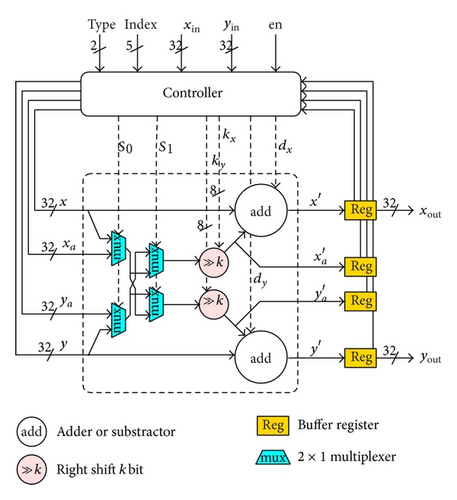
3.3. Adaptive μ-CORDIC Iterations

To improve the computational efficiency, the μ-CORDIC has been modified to perform 6 iterations per cycle as CORDIC-6. As the global clock in a synchronous circuit is determined by the critical path, the maximum timing delay per iteration is 6 cycles (when the index k is 1, Type IV). Therefore, the inner iteration steps of the angles are repeated until they are close to the critical one. The required number of repetitions is quoted in Table 1. For example, when the rotation angle index k is 8, it will repeat three times from the index k = 8 to the index k = 10; when the rotation angle index k is 20, it is repeated six times from the index k = 20 to the index k = 25. On the other hand, we can adjust the number of iterations by selecting the average angle during the last sweep and name it as CORDIC-mean.

4. Experimental Results

4.1. Matlab Simulation

The full CORDIC with 32 iteration steps, the μ-CORDIC with one iteration step, and two different adaptive modes have been tested using numerous random symmetric matrices A of size 8 × 8 to 160 × 160 (i.e., EVD array sizes range from 4 × 4 to 80 × 80). Figure 5(a) shows the average number of sweeps needed to compute the eigenvalues/eigenvectors for each size of the EVD array, where the sweep number increases monotonically.

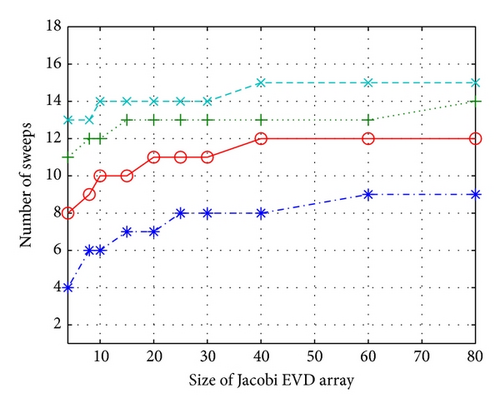
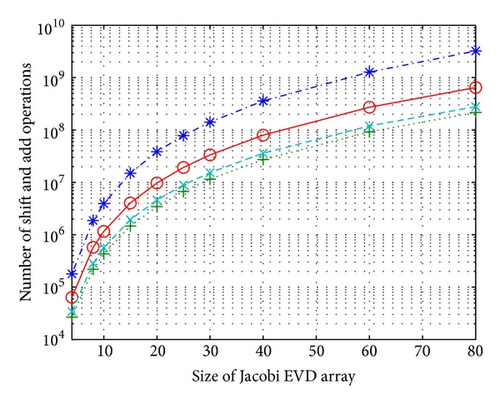
When the Jacobi EVD array size is 10 × 10, the μ-CORDIC requires 12 sweeps while the full CORDIC only requires 6 sweeps per EVD computation. If we adjust the inner rotations to six times, the sweep number will be 10, smaller than the μ-CORDIC but more than the full CORDIC. Note that using the average rotation angle to decide the rotation number as the CORDIC-mean seems to be an unwise method because it requires more sweeps. Although the μ-CORDIC requires double sweeps than the full CORDIC, it actually reduces the number of the inner CORDIC rotations, which results in improved computational complexity. For example, a 10 × 10 array with the Full CORDIC PE needs 6 sweeps × 32 inner CORDIC rotations and the CORDIC-6 needs 10 sweeps × 6 inner CORDIC rotations whereas the μ-CORDIC PE requires only 12 sweeps × 1 inner CORDIC rotation. In Figure 5(b), the average number of shift-add operations required for each rotation method for different sizes of EVD arrays is demonstrated whereas μ-CORDIC needs significantly fewer shift-add operations than others. The adaptive CORDIC-6 method can offer a compromise between the hardware complexity and the computational effort.

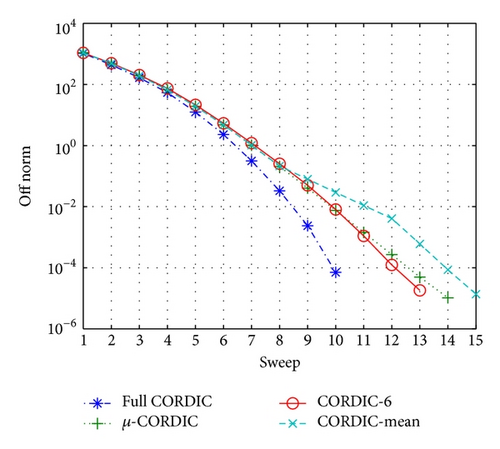
Figure 5(c) shows the off-diagonal Frobenius norm versus the sweep numbers for each array size of 80 × 80 with double floating precision. Each rotation method converges to the predefined stop criteria: . The is the Frobenius norm of the off-diagonal elements of A (i.e., A_off⁡ = A − diag⁡(diag⁡(A))).

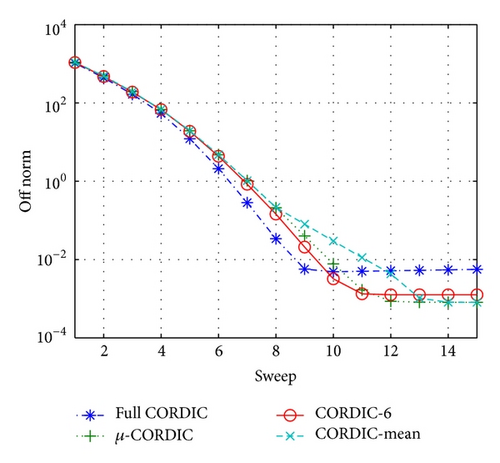
Figure 5(d) shows the reduction of the off-diagonal Frobenius norm versus the sweep numbers for single floating precision. It can be noticed that the off-norms do not reach the convergence criteria, and each size of the EVD array has different stop criteria for each rotation method (default IEEE 754 single). Therefore, we can first analyze the Frobenius norm of the off-diagonal elements in Matlab and then observe it until it reaches its maximal reduction. Afterwards, a lookup table can be generated and directly assign these stop criteria to the target hardware circuit or IP component.

4.2. VLSI Implementation

The μ-CORDIC is modeled and compared to the folded Full CORDIC in VHDL with the resizing feature. These two methods have been integrated into parallel EVD arrays, with sizes 4 × 4 and 10 × 10, through a configurable interface separately. After that, they have been synthesized by using the Synopsys Design Compiler with the TSMC 45 nm standard cell library. Note that the word length is 32 bits with the IEEE 754 single floating precision for both CORDIC methods using the same floating point unit from OpenCORE. Table 2 lists the synthesis results for area, timing delay, and power consumption.

Table 2. Comparison of 4 × 4 and 10 × 10 Jacobi EVD arrays.

	PE array size	Full CORDIC 4 × 4	μ-CORDIC 4 × 4	Full CORDIC 10 × 10	μ-CORDIC 10 × 10
Area	Combinational	0.847 mm²	0.296 mm²	5.143 mm²	1.829 mm²
	Noncombinational	0.390 mm²	0.123 mm²	2.306 mm²	0.833 mm²
	Total	1.237 mm²	0.419 mm²	7.449 mm²	2.662 mm²

Power	Cell	62.283 mW	18.239 mW	388.379 mW	123.215 mW
	Net	0.465 mW	0.433 mW	2.993 mW	2.678 mW
	Leakage	11.909 mW	3.765 mW	86.136 mW	23.966 mW
	Total	74.657 mW	22.437 mW	477.508 mW	149.859 mW

Timing	Critical	4.454 ns	1.213 ns	4.286 ns	2.247 ns
Timing	Frequency	224.5 MHz	824.4 MHz	233.3 MHz	445 MHz

As expected, the combinational logic area and the power consumption of the μ-CORDIC PE are much smaller than the Full CORDIC. Furthermore, in order to determine the time required to compute the EVD of a n × n symmetric matrix, it can be obtained by

()

where n = 8,16,20,30, …, 160, Δ = n/2 − 1.

The total timing delay per EVD operation is defined by the critical timing delay × the number of inner CORDIC rotations × average number of outer sweeps × size of the matrix A. It can be observed that the total operation time is dependent on the relationship between the inner CORDIC rotations and the outer sweeps. Therefore, one obtains a speedup by a factor of 21.4 by reducing the number of inner CORDIC rotations. Although the reduction of power consumption is less significant due to an extra μ-CORDIC’s controller and multiplexers, it actually 6 consumes much less energy per EVD computation due to the shorter computation time. Note that the μ-CORDIC PE requires two inner iterations on average due to the different rotation cycles, from six to one inner iteration, as shown in Table 1. Figure 6 shows the energy consumption for sizes of the array from 4 × 4 to 80 × 80. Both rotation methods consume much less energy than the Full CORDIC, where the 6-CORDIC can obtain a factor of 40.9 and the μ-CORDIC can obtain a factor of 104.3 on average for energy reduction compared to the Full CORDIC.

In [14], a Jacobi single cycle-by-row EVD algorithm [15] has been implemented with a single CORDIC processor. Since it requires a very complex controller and lookup tables, the throughput is not comparable with a real Brent-Luk′s parallel EVD array [13]. In comparison to [13], Full CORDIC for Jacobi Brent-Luk-EVD parallel architecture is implemented in FPGA; however, current configurable device can only perform 4 × 4 EVD array. The experimental results show that performing the unitary rotation in CORDIC processor is a good solution. It required smaller area size, improved the overall computation time, and reduced the energy consumption. Furthermore, the unitary-rotation method can be also applied to other more efficient CORIDC architectures as long as the orthogonality is obtained during CORDIC iterations, such as pipeline CORDIC [16, 17], or implementing the rotators with better adder structures [18, 19].

5. Conclusions

The EVD was computed by the parallel Jacobi method, which was selected as an example for a typical iterative algorithm which exhibits very robust convergence properties. A configurable Jacobi EVD array with both Full CORDIC and μ-CORDIC is implemented in order to further study the tradeoff strategies in design criteria for parallel integrated circuits. The experimental results indicate that the presented μ-CORDIC method can reduce the size of the combinational logic, speed up the overall computation time, and improve the energy consumption.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgment

The authors would like to thank the National Science Council of Taiwan for the support under the contract of NSC 101-2218-E-150-001.

References

1 Aggarwal S. and Khare K., CORDIC-based window implementation to minimise area and pipeline depth, IET Signal Processing. (2013) 7, no. 5, 427–435, https://doi.org/10.1049/iet-spr.2012.0021, MR3112719.
Google Scholar
2 Ahmed H. M., Delosme J., and Morf M., Highly concurrent computing structure for matrix arithmetic and signal processing, IEEE Computer Magazine. (1982) 15, no. 1, 65–82, https://doi.org/10.1109/MC.1982.1653828, 2-s2.0-0019928904.
Google Scholar
3 Ahmedsaid A., Amira A., and Bouridane A., Improved SVD systolic array and implementation on FPGA, Proceedings of the IEEE International Conference on Field-Programmable Technology, 2003, 3–42.
Google Scholar
4 Andraka R., Survey of CORDIC algorithms for FPGA based computers, Proceedings of the ACM/SIGDA 6th International Symposium on Field Programmable Gate Arrays (FPGA ′98), February 1998, 191–200, 2-s2.0-0031645163.
Google Scholar
5 Bravo I., Jiménez P., Mazo M., Lázaro J. L., and Gardel A., Implementation in FPGAS of Jacobi method to solve the eigenvalue and eigenvector problem, Proceedings of the International Conference on Field Programmable Logic and Applications (FPL ′06), August 2006, Madrid, Spain, 1–4, https://doi.org/10.1109/FPL.2006.311301, 2-s2.0-46249102178.
Google Scholar
6 Brent R. P. and Luk F. T., The solution of singular-value and symmetric eigenvalue problems on multiprocessor arrays, SIAM Journal on Scientific and Statistical Computing. (1985) 6, no. 1, 69–84, https://doi.org/10.1137/0906007, MR773282.
Google Scholar
7 Golub G. H. and van Loan C. F., Matrix Computations, 1996, 3rd edition, Johns Hopkins University Press, Baltimore, Md, USA, MR1417720.
Google Scholar
8 Götze J. and Hekstra G. J., An algorithm and architecture based on orthonormal μ-rotations for computing the symmetric EVD, Integration, the VLSI Journal. (1995) 20, no. 1, 21–39, https://doi.org/10.1016/0167-9260(95)00016-X, ZBL0875.68557, 2-s2.0-0029545884.
Google Scholar
9 Götze J., Paul S., and Sauer M., An efficient Jacobi-like algorithm for parallel eigenvalue computation, IEEE Transactions on Computers. (1993) 42, no. 9, 1058–1065, https://doi.org/10.1109/12.241595, MR1252315, 2-s2.0-0027658980.
Google Scholar
10 Hakkarainen A., Werner J., Dandekar K. R., and Valkama M., Widely-linear beamforming and RF impairment suppression in massive antenna arrays, Journal of Communications and Networks. (2013) 15, no. 4, 383–397, https://doi.org/10.1109/JCN.2013.000069.
Google Scholar
11 Klauke S. and Götze J., Low power enhancements for parallel algorithms, Proceedings of the IEEE International Symopsium on Circuits and Systems, 2001, 234–237.
Google Scholar
12 Liu Y., Bouganis C.-S., and Cheung P. Y. K., Hardware architectures for eigenvalue computation of real symmetric matrices, IET Computers and Digital Techniques. (2009) 3, no. 1, 72–84, https://doi.org/10.1049/iet-cdt:20080008, 2-s2.0-58049097176.
Web of Science® Google Scholar
13 Meher P. K. and Park S. Y., CORDIC designs for fixed angle of rotation, IEEE Transactions on Very Large Scale Integration (VLSI) Systems. (2013) 21, no. 2, 217–228, https://doi.org/10.1109/TVLSI.2012.2187080, 2-s2.0-84872892494.
Google Scholar
14 Parhi K. K. and Nishitani T., Digial Signal Processing for Multimedia Systems, 1999, Marcel Dekker.
Google Scholar
15 Purohit S. and Margala M., Investigating the impact of logic and circuit implementation on full adder performance, IEEE Transactions on Very Large Scale Integration (VLSI) Systems. (2012) 20, no. 7, 1327–1331, https://doi.org/10.1109/TVLSI.2011.2157543, 2-s2.0-84862024132.
Google Scholar
16 Ramkumar B. and Kittur H. M., Low-power and area-efficient carry select adder, IEEE Transactions on Very Large Scale Integration (VLSI) Systems. (2012) 20, no. 2, 371–375, https://doi.org/10.1109/TVLSI.2010.2101621, 2-s2.0-84856292234.
Google Scholar
17 Rusek F., Persson D., Lau B. K., Larsson E. G., Marzetta T. L., Edfors O., and Tufvesson F., Scaling up MIMO: opportunities and challenges with very large arrays, IEEE Signal Processing Magazine. (2013) 30, no. 1, 40–46.
Google Scholar
18 Sun C.-C. and Götze J., VLSI circuit design concept for parallel iterative algorithms in nanoscale, Proceedings of the 9th International Symposium on Communications and Information Technology (ISCIT ′09), September 2009, Icheon, Republic of Korea, 688–692, https://doi.org/10.1109/ISCIT.2009.5341155, 2-s2.0-74549203242.
Google Scholar
19 Walther J. S., A unified algorithm for elementary functions, Proceedings of the Spring Joint Computer Conference, 1971, 379–385.
Google Scholar

Citing Literature

All articles

Parallel Jacobi EVD Methods on Integrated Circuits

Abstract

1. Introduction