This paper addresses the problem of multichannel autoregressive (MAR) parameter estimation in the presence of spatially correlated noise by steepest descent (SD) method which combines low-order and high-order Yule-Walker (YW) equations. In addition, to yield an unbiased estimate of the MAR model parameters, we apply inverse filtering for noise covariance matrix estimation. In a simulation study, the performance of the proposed unbiased estimation algorithm is evaluated and compared with existing parameter estimation methods.

1. Introduction

The noisy MAR modeling has many applications such as high resolution multichannel spectral estimation [1], parametric multichannel speech enhancement [2], MIMO-AR time varying fading channel estimation [3], and adaptive signal detection [4].

When the noise-free observations are available, the Nuttall-Strand method [5], the maximum likelihood (ML) estimator [6], and the extension of some standard schemes in scalar case to multichannel can be used for estimation of MAR model parameters. The relevance of the Nuttall-Strand method is explained in [7] by carrying out a comparative study between these methods. The noise-free MAR estimation methods are sensitive to the presence of additive noise in the MAR process which limits their utility [1].

The modified Yule-Walker (MYW) method is a conventional method for noisy MAR parameter estimation. This method uses estimated correlation at lags beyond the AR order [1]. The MYW method is perhaps the simplest one from the computational point of view [8], but it exhibits poor estimation accuracy and relatively low efficiency due to the use of large-lag autocovariance estimates [8]. Moreover, numerical instability issues may occur when it is used in online parameter estimation [9].

The least-squares (LS) method is another method for noisy MAR parameter estimation. The additive noise causes the least-squares (LS) estimates of MAR parameters to be biased. In [10] an improved LS (ILS) based method has been developed for estimation of noisy MAR signals. In this method, bias correction is performed using observation noise covariance estimation.

The method proposed in [10], denoted by vector ILS based (ILSV) method, is an extension of Zheng’s method [11] to the multichannel case. In the ILSV method, the channel noises can be correlated and no constraint is imposed on the covariance matrix of channel noises. Nevertheless this method has poor convergence when the SNR is low.

In [12], the ILSV algorithm is modified using symmetry property of the observation covariance matrix which is named an advanced least square vector (ALSV) algorithm. One step called symmetrisation is added to the ILSV algorithm to estimate the observation noise covariance matrix.

In [13, 14], methods based on errors-in-variables and cross coupled, Kalman and H_∞, filters are suggested, respectively. These methods are also an extension of the scalar methods presented in [15] and [16, 17], respectively. In these methods, the observation noise covariance matrix is assumed to be a diagonal matrix. This assumption means that the channel noises are uncorrelated. These methods are not suitable for spatially correlated noise case.

Note that cross coupled filter idea consists of using two mutually interactive filters. Each time a new observation is available, the signal is estimated using the latest estimate value of the parameters, and conversely the parameters are estimated using the latest a posteriori signal estimate.

In this paper, we combine low-order and high-order YW equations in a new scheme and use adaptive steepest descent (SD) algorithm to estimate the parameters of the MAR process. We also apply the inverse filtering idea for observation noise covariance matrix estimation. Finally we can theoretically perform the convergence analysis of the proposed method. Using computer simulations, the performance of the proposed algorithm is evaluated and compared with that of the LS, MYW, ILSV, and ALSV methods in spatially correlated noise case. Note that we do not do comparisons with [13, 14] because they assume that the channel noises are uncorrelated.

The proposed estimation algorithm provides more accurate parameter estimation. The convergence behaviour of the proposed method is better than those of the ILSV and the ALSV methods.

2. Data Model

A real noisy m-channel AR signal can be modeled as

()

where e(n) is the m × 1 input noise vector and z(n) is the m × 1 MAR output noise vector. A_i’s (i = 1,2, …, p) are the m × m MAR parameter matrices, and y(n) is the m × 1 observed noise vector. The noises e(n) and w(n) are assumed to be zero-mean stationary white noises with the m × m covariance matrices given by

()

where δ_l is the Kronecker delta and Σ_e and Σ_w are the unknown input noise covariance matrix and the observation noise covariance matrix which are generally nondiagonal. This means that the observation noise is spatially correlated. E{·} is the expectation operator and T denotes the transpose operation.

In this data model, we have the following assumptions.

(i)
The AR order p and the number of channels m are known.
(ii)
The MAR parameter matrices A_i are constrained such that the roots of
()

lie inside the unit circle, where

, I_m is the m × m identity matrix, and det denotes determinant of a matrix. This condition on the matrices A_i guarantees the stability of the MAR model [1]. Note that the roots of (3) are poles of the MAR model.

(iii)
The observation noise w(n) is uncorrelated with the input noise e(n); that is, E{w(n)e(k) ^T} = 0 for all n and k.

Using (1), we can write the following linear regression for y(n):

()

where A is the mp × m parameter matrix defined as

()

and g(n) is the mp × 1 regression vector defined as

()

The m × 1 equation error vector ε(n) is

()

where

()

The covariance matrices of ε(n) and y(n) are given as

()

where A₀ = −I_m.

The main objective in this paper is to estimate A, Σ_w, and Σ_e using the given samples {y(1), y(2), …, y(N)}.

3. Steepest Descent Algorithm for Noisy MAR Models

The proposed estimation algorithm uses steepest descent method. It iterates between the following two steps until convergence: (I) given noise covariance matrix, estimate MAR matrices using steepest descent method; (II) given MAR matrices, estimate noise covariance matrix based on inverse filtering idea.

3.1. MAR Parameter Estimation Given Observation Noise Covariance Matrix

The Yule-Walker equations for the noisy MAR process given by (4) are

()

Evaluating (11) for l = 1, …, p and using R_y(l) = R_y(−l) ^T give the following system of linear equations:

()

where

()

and R_w is a block-diagonal mp × mp matrix given by

()

Evaluating (11) for l = p + 1, …, p + q and using R_y(l) = R_y(−l) ^T give the following modified Yule-Walker (MYW) equations:

()

where

()

and q is an arbitrary nonnegative integer.

Combining the low-order Yule-Walker equations given by (12) and the high-order Yule-Walker equations given by (15), we obtain

()

where

()

Premultiplying (17) by

, we obtain

()

where

()

And R_H of dimension mp × m(p + q) can be partitioned as

()

where the dimensions of R_H1 and R_H2 are mp × mp and mp × mq, respectively.

Substituting (19) and (22) into (20), we get

()

If R_w is assumed to be known, we can iteratively estimate A using steepest descent algorithm as follows:

()

where μ is the step size parameter and A_H, R_H1 can be estimated from the observations. We can also control the stability and rate of convergence of the algorithm by changing μ. The above equation is converged if μ is selected between zero and 2/(1 − λ_min⁡) where λ_min⁡ is the maximum eigenvalue of the R_H1R_w matrix. Furthermore if we set μ = 1 and q = 0 in (24), it is changed to

()

where

, which is previously derived in [8].

3.2. Application of Inverse Filtering for Estimation of Observation Noise Covariance Matrix Given MAR Matrices

If the observed process is filtered by MAR matrices, the output process of the filter is obtained as

()

By evaluating (9) for l = 1, we can obtain

()

We can rewrite (27) as

()

We solve (28) as follows:

()

where r_ε = vec⁡(R_ε(1) ^T) and vec is a column vectorization operator; that is,

()

By assuming

, symmetry property of

, we can improve estimate as [12]

()

where unvec is the inverse operation of vec.

Using (26) R_ε(1) is evaluated from the observed signal as

()

In (32), A is unknown. So, we will use a recursive algorithm for estimating Σ_w and A. This algorithm is discussed in Section 3.3.

Now, we assume that Σ_w and A are known and derive an estimate for Σ_e.

Evaluating (9), for l = 0, we obtain

()

where

()

3.3. The Algorithm

The results derived in previous sections and subsections are summarized to propose a recursive algorithm for estimating Σ_w and A_i’s (i = 1,2, …, p). The improved least-squares algorithm for multichannel processes based on inverse filtering (IFILSM) is as follows.

Step 1. Compute autocovariance estimates by means of given samples {y(1), y(2), …, y(N)}:

()

and use them to construct the covariance matrix estimates

, and

Step 2. Initialize i = 0, where i denotes the iteration number. Then, compute the estimate

()

Step 3. Set i = i + 1 and calculate the estimate of observation noise covariance matrix :

()

Step 4. Perform the bias correction

()

Step 5. If

()

where ∥·∥ is the Euclidean norm and δ is an appropriate small positive number, the convergence is achieved and the iteration process must be terminated; otherwise, go to Step 3.

Step 6. Estimate Σ_e via (33):

()

4. Simulation Result

In simulation study, we have compared the IFILSM method with the other existing methods. Two examples have been considered: first frequency estimation and second synthetic noisy MAR model estimation. In all simulations, we set μ = 1 for the proposed IFILSM algorithm.

4.1. Estimating the Frequency of Multiple Sinusoids Embedded in Spatially Colored Noise

Consider several sinusoidal signals in spatially colored noise as follows:

()

It is well known that z(n) can be modeled as an MAR (2L) process with zero driving noise vector (e(n) = 0). So, we can apply the method proposed in the previous subsection to estimate the frequency of sinusoidal signals corrupted with spatially colored observation noise. Note that the frequency of sinusoids can be estimated by locating the peaks in the MAR spectrum.

Example 1. We consider N = 500 data samples of a signal comprised of two sinusoids corrupted with spatially colored noise. Consider y(n) as follows:

()

where ω₁ = 2π0.1, ω₂ = 2π0.3, φ₁, φ₂ are independent random phases uniformly distributed over [0, 2π], and w(n) is Gaussian spatially colored noise having the following covariance matrix:

()

The signal-to-noise ratio (SNR) of each channel is defined as

()

which is set to 5 and 10 dB. The number of trials M is set to 1000 and the parameter q in the IFILSM and MYW methods is set to 4. The δ in the ILSV, ALSV, and IFILSM methods is set to 0.01. We compare the proposed method with the LS, MYW, ALSV, and ILSV methods in terms of mean square error (MSE) of frequency estimates. Note that other existing methods cannot work in the spatially correlated observation noise. In Table 1, we tabulate the MSEs in terms of dB for the LS, MYW, ALSV, ILSV, and proposed methods. We see that, from the table, the proposed method has the best performance.

Table 1. Simulation results (M = 1000, N = 500, SNR = 5, 10 dB, ω₁ = 2π0.1, and ω₂ = 2π0.3).

SNR	5 dB	5 dB	10 dB	10 dB
Methods	MSE1 (dB)	MSE2 (dB)	MSE1 (dB)	MSE2 (dB)
IFILSM	−42.18	−47.04	−51.11	−60.06
ILSV	−32.64	−41.91	−42.22	−50.51
ALSV	−32.35	−42.76	−42.33	−51.36
LS	−5.75	−23.02	−32	−31.27
MYW	−37.58	−45.05	−46.82	−51.94

4.2. Synthetic MAR Processes

Example 2. Consider a noisy MAR model with p = 2, m = 2, and coefficient matrices

()

The driving process e(n) and observation noise w(n) covariance are mutually uncorrelated Gaussian temporally white and spatially correlated processes with covariance matrices

()

We compare the ILSV, the ALSV, and the proposed IFILSM method in terms MSE of MAR coefficient estimate and the convergence probability defined as

()

where M is the number of runs that an iterative algorithm is converged and M_t is the total number of runs. We set the parameters of the algorithms M = 1000 and the parameter q in the IFILSM method is set to 4. The δ in the ILSV, ALSV, and IFILSM methods is set to 0.01.

In Case 1 and Case 2 SNR for each channel is set to 15 and 10 dB, respectively. In this example data samples N are changed from 1000 to 4000 with step size 1000. The MSE and P values are plotted in Figures 1, 2, and 3 versus N, respectively. The probability of convergence is one for all algorithms in Case 1 and the figure is not plotted here. From the figures, we can see that the accuracy and the convergence of the IFILSM are better than the ILSV and ALSV methods. Note that the ILSV and ALSV methods have poor convergence when SNR is lower or equal to 10 dB. It can be seen from the figures that the performance of the all algorithms is constant over the sample size because autocovariance estimates of the observations are not changed in this rage of data sample size.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

MSE values of MAR matrices estimate versus data samples; M = 1000, SNR = 15 dB.

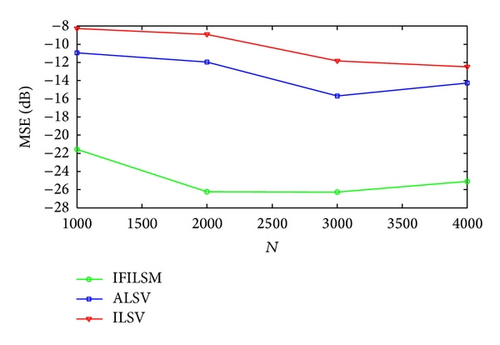
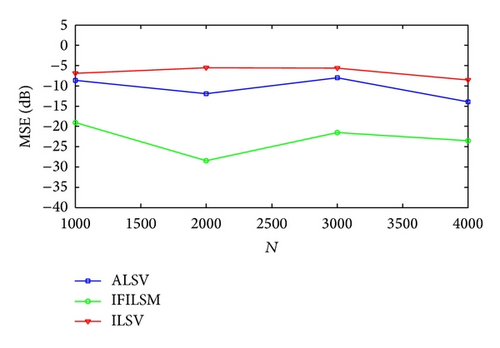
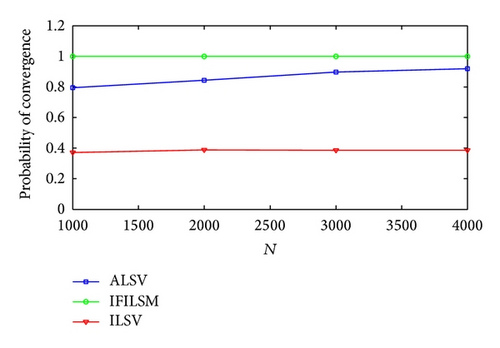
5. Conclusion

Steepest descent (SD) algorithm is used for estimating noisy multichannel AR model parameters. The observation noise covariance matrix is nondiagonal; this means that the channel noises are assumed to be spatially correlated. The inverse filtering idea is used to estimate the observation noise covariance matrix. Computer simulations showed that the proposed method has better performance and convergence than the ILSV and the ALSV methods.

Conflict of Interests

The author declares that there is no conflict of interests regarding the publication of this paper.

Appendix

The following result discusses the convergence conditions of the proposed algorithm.

Theorem A.1. The necessary and sufficient condition for the convergence of the proposed algorithm is to require that the step size parameter μ satisfy the following condition:

()

where λ_min⁡ is the minimum eigenvalue of the R_H1R_w matrix.

Proof. Defining estimation error matrix x⁽ⁱ⁾ = A⁽ⁱ⁾ − A, substituting A − A_H − R_H1R_wA = 0 into (24), and using x⁽ⁱ⁾ = A⁽ⁱ⁾ − A, we obtain

()

The eigenvalues of I − μ(I − R_H1R_w) are 1 − μ(1 − λ_i) where λ_i = λ_i(R_H1R_w) is between 0 and 1.

If −1 < 1 − μ(1 − λ_i) < 1, then lim⁡_i→∞x⁽ⁱ⁾ = 0. In this case, we have 0 < μ < 2/(1 − λ_i), and their intersection is 0 < μ < 2/λ_max⁡(I − R_H1R_w) = 2/(1 − λ_min⁡).

References

1 Kay S. M., Modern Spectral Estimation: Theory and Application, 1988, Prentice-Hall, Englewood Cliffs, NJ, USA.
Google Scholar
2 Srinivasan S., Aichner R., Kleijn W. B., and Kellermann W., Multichannel parametric speech enhancement, IEEE Signal Processing Letters. (2006) 13, no. 5, 304–307, 2-s2.0-33645803631, https://doi.org/10.1109/LSP.2005.863819.
Google Scholar
3 Komninakis C., Fragouli C., Sayed A. H., and Wesel R. D., Multi-input multi-output fading channel tracking and equalization using Kalman estimation, IEEE Transactions on Signal Processing. (2002) 50, no. 5, 1065–1076, 2-s2.0-0036571056, https://doi.org/10.1109/78.995063.
Google Scholar
4 Wang P., Li H., and Himed B., A new parametric GLRT for multichannel adaptive signal detection, IEEE Transactions on Signal Processing. (2010) 58, no. 1, 317–325, 2-s2.0-72949085815, https://doi.org/10.1109/TSP.2009.2030835.
Google Scholar
5 Marple S., Digital Spectral Analysis with Applications, 1987, Prentice-Hall, Englewood Cliffs, NJ, USA.
Google Scholar
6 Pham D. T. and Tong D. Q., Maximum likelihood estimation for a multivariate autoregressive model, IEEE Transactions on Signal Processing. (1994) 42, no. 11, 3061–3072, 2-s2.0-0028539915, https://doi.org/10.1109/78.330366.
Google Scholar
7 Schlogl A., A comparison of multivariate autoregressive estimators, Signal Process. (2006) 86, no. 9, 2426–2429.
Google Scholar
8 Nehorai A. and Stoica P., Adaptive algorithms for constrained ARMA signals in the presence of noise, IEEE Transactions on Acoustics, Speech, and Signal Processing. (1988) 36, no. 8, 1282–1291, 2-s2.0-0024056525, https://doi.org/10.1109/29.1656.
Google Scholar
9 Zheng W. X., Fast identification of autoregressive signals from noisy observations, IEEE Transactions on Circuits and Systems II: Express Briefs. (2005) 52, no. 1, 43–48, 2-s2.0-12544258985, https://doi.org/10.1109/TCSII.2004.838435.
Google Scholar
10 Mahmoudi A. and Karimi M., Estimation of the parameters of multichannel autoregressive signals from noisy observations, Signal Processing. (2008) 88, no. 11, 2777–2783, 2-s2.0-47749121736, https://doi.org/10.1016/j.sigpro.2008.06.004.
Google Scholar
11 Zheng W. X., Autoregressive parameter estimation from noisy data, IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing. (2000) 47, no. 1, 71–75, 2-s2.0-0033908205, https://doi.org/10.1109/82.818897.
Google Scholar
12 Qu X. M., Zhou J., and Luo Y. T., A new noise-compensated estimation scheme for multichannel autoregressive signals from noisy observations, Journal of Supercomputing. (2011) 58, no. 1, 34–49, 2-s2.0-80054920262, https://doi.org/10.1007/s11227-010-0530-z.
Google Scholar
13 Petitjean J., Grivel E., Bobillet W., and Roussilhe P., Multichannel AR parameter estimation from noisy observations as an errors-in-variables issue, Signal, Image and Video Processing. (2010) 4, no. 2, 209–220.
Google Scholar
14 Jamoos A., Grivel E., Shakarneh N., and Abdel-Nour H., Dual optimal filters for parameter estimation of a multivariate autoregressive process from noisy observations, IET Signal Processing. (2011) 5, no. 5, 471–479, 2-s2.0-80051686910, https://doi.org/10.1049/iet-spr.2010.0066.
Google Scholar
15 Labarre D., Grivel E., Berthoumieu Y., Todini E., and Najim M., Consistent estimation of autoregressive parameters from noisy observations based on two interacting Kalman filters, Signal Processing. (2006) 86, no. 10, 2863–2876, 2-s2.0-33745698076, https://doi.org/10.1016/j.sigpro.2005.12.001.
Google Scholar
16 Labarre D., Grivel E., Najim M., and Christov N., Dual H_∞ algorithms for signal processing-application to speech enhancement, IEEE Transactions on Signal Processing. (2007) 55, no. 11, 5195–5208, 2-s2.0-36248960444, https://doi.org/10.1109/TSP.2007.899587.
Google Scholar
17 Bobillet W., Diversi R., Grivel E., Guidorzi R., Najim M., and Soverini U., Speech enhancement combining optimal smoothing and errors-in-variables identification of noisy AR processes, IEEE Transactions on Signal Processing. (2007) 55, no. 12, 5564–5578, 2-s2.0-36749023475, https://doi.org/10.1109/TSP.2007.898787.
Google Scholar

Citing Literature

All articles

Adaptive Algorithm for Multichannel Autoregressive Estimation in Spatially Correlated Noise

Abstract

1. Introduction

2. Data Model

3. Steepest Descent Algorithm for Noisy MAR Models

3.1. MAR Parameter Estimation Given Observation Noise Covariance Matrix

3.2. Application of Inverse Filtering for Estimation of Observation Noise Covariance Matrix Given MAR Matrices

3.3. The Algorithm

4. Simulation Result

4.1. Estimating the Frequency of Multiple Sinusoids Embedded in Spatially Colored Noise

4.2. Synthetic MAR Processes

5. Conclusion

Conflict of Interests

Appendix

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Adaptive Algorithm for Multichannel Autoregressive Estimation in Spatially Correlated Noise

Abstract

1. Introduction

2. Data Model

3. Steepest Descent Algorithm for Noisy MAR Models

3.1. MAR Parameter Estimation Given Observation Noise Covariance Matrix

3.2. Application of Inverse Filtering for Estimation of Observation Noise Covariance Matrix Given MAR Matrices

3.3. The Algorithm

4. Simulation Result

4.1. Estimating the Frequency of Multiple Sinusoids Embedded in Spatially Colored Noise

4.2. Synthetic MAR Processes

5. Conclusion

Conflict of Interests

Appendix

References

Citing Literature

Figures

References

Related

Information