This paper presents an improvement in power flow calculation based on current injection method by introducing optimization factor. In the method proposed by this paper, the PQ buses are represented by current mismatches while the PV buses are represented by power mismatches. It is different from the representations in conventional current injection power flow equations. By using the combined power and current injection mismatches method, the number of the equations required can be decreased to only one for each PV bus. The optimization factor is used to improve the iteration process and to ensure the effectiveness of the improved method proposed when the system is ill-conditioned. To verify the effectiveness of the method, the IEEE test systems are tested by conventional current injection method and the improved method proposed separately. Then the results are compared. The comparisons show that the optimization factor improves the convergence character effectively, especially that when the system is at high loading level and R/X ratio, the iteration number is one or two times less than the conventional current injection method. When the overloading condition of the system is serious, the iteration number in this paper appears 4 times less than the conventional current injection method.

1. Introduction

Power flow studies are necessary for planning, operating, economic scheduling, and other analysis, such as transient stability, voltage stability, and contingency studies. The tasks of power flow calculation are to solve the steady-state operating conditions of power systems based on the operation modes and the wiring of the systems. Different power flow methods have emerged and continue to be developed with the changing needs.

The conventional power flow solution comprises power equations expressed in terms of rectangular or polar coordinates. Many important contributions have been reported in this area [1–3]. To improve the convergence characteristic of Gauss-Seidel method, the Newton-Raphson method was introduced. The NR method was once considered the state of the art power-flow technique and widely accepted in industry applications. However, the main disadvantage of the Newton-Raphson method is the necessity for factorizing and updating the Jacobian matrix during the iterative solution process [4]. To solve this problem, Fast Decoupled power flow method was proposed to speed up the iteration process of the NR method and decrease the required minimum memory storage. Nevertheless, the convergence rate of the decoupled NR is influenced by the ill-conditioned case, such as when a system has high ratio of line R/X [5–8]. Some other methods have been presented in other forms, such as the use of sequence component frame [9–11] and the method based on the loop frame of reference [12].

In [13], a new power flow method based on current injection was presented, in which the current injection equations are written in rectangular coordinates. The Jacobian matrix is composed of 6 × 6 block matrices and has the same structure as the nodal admittance matrix. By using this method, the Jacobian matrix can be updated faster than using conventional NR power flow method in the case of PQ buses. However, in the case of the existence of PV buses, the current injection mismatch power flow method was presented to improve the convergence character of current injection method [14, 15]. The improvement in [16] increased the number of required equations to three for each PV bus. The paper [17] presented a new representation of PV buses in revised current injection power flow method to reduce the number of required equations and to improve the convergence character of well- and ill-conditioned systems, while the elements related to PV buses have to be changed during the iteration process. In [18] a development of power flow calculation for ill-conditioned system was presented. The fact that “the Taylor series expansion of the load flow equations is expressed up to the third term completely and the final term has the same form but different variable as the first term” was used in [18]. Following the main ideas presented in [18], which is called Iwamoto’s method in [15], a new second order power flow method was proposed. This method is useful for heavily loaded and overloaded systems as well as ill-conditioned distribution systems.

This paper improved the current injection method presented in [17] following the main idea in [18]. The optimization presented in [18] is briefly described here firstly to make the paper clear. Then the improved method, results, and conclusions are presented.

2. Current Injection Power Flow

The basic current injection method proposed in [17] is used in this paper. The combined power and current injection mismatches power flow formulation can be calculated from the following:

()

where ΔI_rk: real parts of current mismatch at bus k, ΔI_mk: imaginary parts of current mismatch at bus k, ΔP_k: active power mismatch at bus k, ΔV_rk: real voltage component correction at bus k, ΔV_mk: imaginary voltage component correction at bus k, and Δδ_k: voltage angle correction at bus k.

2.1. Equations for PQ Buses

The current mismatch for a given bus k is

()

where

: complex conjugated voltage phasor at bus k,

: specified active and reactive net powers at bus k, Y_ki = G_ki + jB_ki: bus admittance matrix element, and E_i: voltage phasor at bus i. Consider

()

where P_gk, Q_gk: active and reactive powers of generators for bus k and P_lk, Q_lk: active and reactive powers of loads for bus k.

Equation (2) can be expanded into its real and imaginary components:

()

where V_rk: real voltage component at bus k and V_mk: imaginary voltage component at bus k.

Equations (4) and (5) are written in compact forms:

()

where

: specified real and imaginary parts of current at bus k,

: calculated real and imaginary parts of current at bus k.

Using the Newton-Raphson solution algorithm, the elements in (1) for all buses as being of the PQ type are given by

()

The diagonal elements are given by

()

The elements a_k, b_k, c_k, and d_k are presented in Appendix A of [13].

The following equation is expression of current mismatches in (1):

()

2.2. Representation of PV Buses

The calculated active power at assumed bus k can be calculated by

()

where δ_ki = δ_k − δ_i, δ_k: voltage phase angle at bus k.

In the Jacobian matrix of (1), the elements related to buses of PV type are given as follows.

Diagonal elements

()

Off diagonal elements

()

3. Description of Iwamoto’s Method

The method presented in [18] is described briefly here to make the improved method proposed in next part clearly. The conventional power flow equations in the rectangular coordinates are

()

The Taylor series expansion of (13) turns out to be

()

where x_e: estimate of x, J: Jacobian matrix, and Δx: error (correction vector).

Moving all the right-hand side of (14) to the left-hand side

()

To obtain the solution of this equation, it denotes by μ, the step size optimization factor. Applying this factor to this equation, then it follows that

()

It can be rewritten as

()

where

()

The following cost function is considered to determine the value of the μ in a least squared sense:

()

The optimization solution is given by

()

Namely,

()

where

()

The state vector for the next iteration is given by

()

4. Improvement in Current Injection Method

4.1. Parameters for PQ Buses

The improved method is based on the current injection method by defining a step size optimization factor. The equation (5) is the expression of imaginary current injection related to bus k. Neglecting all terms of order higher than two, we then get

()

Hence, the following equations can be got based on the theory in part 3:

()

In a similar way, the following equations can be obtained

()

Thus, the parameters can be obtained as follows

()

4.2. Parameters for PV Buses

From (1) for a PV bus one has

()

Using the same method as parameters for PQ buses, the following equations can be obtained

()

5. Results

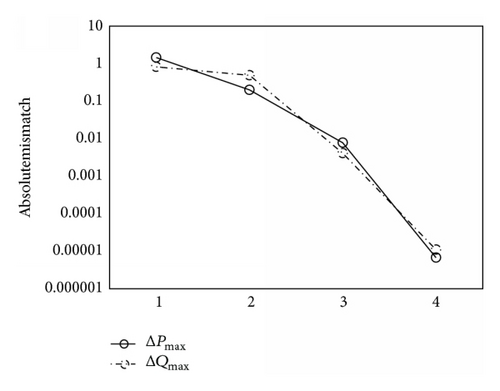
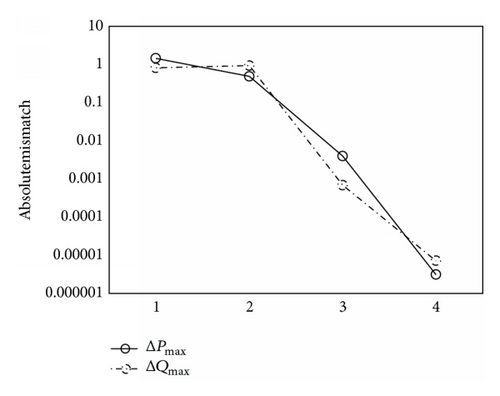
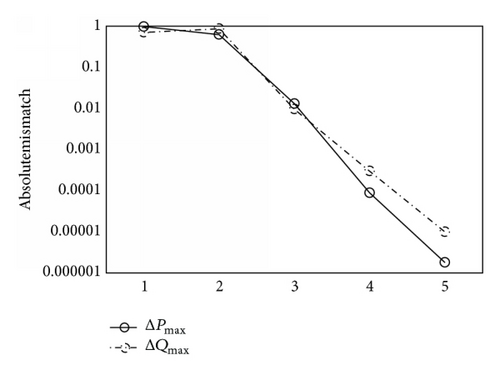
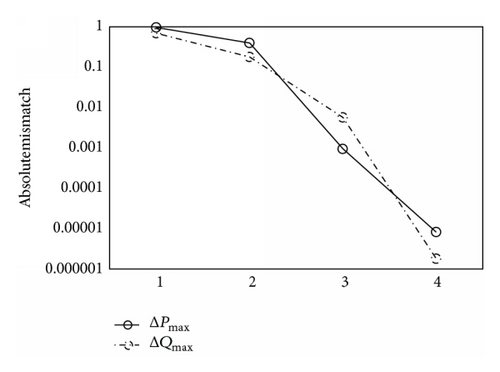
This paper used MATLAB to implement the program of power flow method proposed. IEEE 30-bus and 118-bus test system are tested here. Firstly the validity of the improved method proposed is proven. Here the systems are tested as symmetrical systems. Tables 1 and 2 show a part of the results. Then the results obtained by conventional current injection and the improved method proposed, respectively, are compared. Figures 1 and 2 show the iteration characteristics of IEEE 30-bus test system using the two different methods and Figures 3 and 4 show the results of IEEE 118-bus system in the same way.

Table 1. Parts of the iteration results of 30-bus system.

Bus	Type	Voltage (p.u.)	θ_k (°)
1	0	1.0500	0.0000
5	2	1.0100	−6.5044
13	2	1.0500	−6.3295
20	1	1.0183	−9.4974
29	1	0.9972	−10.6400

0—slack bus, 1—PQ bus, 2—PV bus.

Table 2. Parts of the iteration results of 118-bus system.

Bus	Type	Voltage (p.u.)	θ_k (°)
1	2	0.9550	−7.7063
10	2	1.0500	16.2400
26	2	1.0500	8.4671
43	1	0.9632	−8.6993
57	1	0.9714	−3.2338
65	2	1.0050	5.1198
69	0	1.0350	0.0000
87	2	1.0150	14.7054
99	2	1.0100	6.3423
116	2	1.0050	3.9203

0—slack bus, 1—PQ bus, 2—PV bus.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Iteration characteristics of IEEE 30-bus system using conventional current injection method.

Tables 3 and 4 compare the conventional current injection method and the improved method proposed here when the system has high R/X ratios and compare the two methods when the system is operating in overloaded condition.

Table 3. Number of iterations for different R/X ratios-30-bus system.

R/X ratio	Method
R/X ratio	Conventional current injection method	The improved method proposed
0.5	2	2
1	2	2
4	3	3
6	4	3
8	6	4

Table 4. Number of iterations for different loading levels-30-bus system.

Loading	Method
Loading	Conventional current injection method	The improved method proposed
1	2	2
4	3	2
6	5	3
10	8	4
15	No convergence	6

(a) Validity of the Method. Tables 1 and 2 show the results of the iteration and present the validity of the improved method. The voltage amplitudes and angles are reasonable and acceptable. At the same time the feasibility of the method is proved.

(b) Convergence Characteristic. The iteration convergence criterion for the program of the improved method proposed is that the maximum active power mismatch and the maximum reactive power mismatch are both less than the tolerance. The results presented in Figures 1–4 show that the convergence characteristic of the improved method proposed is better than the conventional current injection method.

(c) High R/X Ratio. Many power flow methods always have bad convergence characteristic if the system has high R/X ratio. In Table 3 the R/X ratios are divided into five levels. When the system has high X/R ratio, both the two methods have good convergence characteristic, but with the increase of R/X ratio the advantage of the improved method proposed becomes obvious; the iteration number is one or two times less than the conventional current injection method.

(d) Overloading. The comparison of the iteration number for different loading cases is shown in Table 4. In this case the system is in overloading condition. In Table 4, five loading cases are presented. There has been little difference between the two methods when the overloading of the system is not serious. However, when the condition becomes more serious the iteration number of the improved method proposed appears 4 times less than the conventional current injection method. Even more, when the convergence characteristic of the improved method proposed is still acceptable when overloading is serious, the conventional current injection method shows no convergence.

6. Conclusions

This paper has presented improvement in power flow calculation based on current injection method by introducing an optimization factor. Unlike other current injection methods, the PV buses are represented by power mismatches here. The results have demonstrated the good performance of the improved method proposed in this paper. By using optimization factor the iteration character got improved. Even when the system has high R/X ratio or operates in overloaded conditions, good results could be got by using this method.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

This work was supported in part by the National Natural Science Foundation of China (no. 51205046) and the Fundamental Research Funds for the Central Universities (nos. CDJZR170008, 106112014CDJZR175501). The constructive comments provided by the anonymous reviewers and the editors are also greatly appreciated.

References

1 Ying-Yi H. and Fu-Ming W., Development of three-phase Newton optimal power flow for studying imbalance/security in transmission systems, Electric Power Systems Research. (2000) 55, no. 1, 39–48, https://doi.org/10.1016/S0378-7796(99)00093-0, 2-s2.0-0033728317.
10.1016/S0378-7796(99)00093-0
Web of Science® Google Scholar
2 Stott B., Review of load-flow calculation methods, Proceedings of the IEEE. (1974) 62, no. 7, 916–929, https://doi.org/10.1109/PROC.1974.9544, 2-s2.0-0016079843.
10.1109/PROC.1974.9544
Web of Science® Google Scholar
3 Expósito A. G. and Ramos E. R., Augmented rectangular load flow model, IEEE Transactions on Power Systems. (2002) 17, no. 2, 271–276, https://doi.org/10.1109/TPWRS.2002.1007892, 2-s2.0-0036577512.
10.1109/TPWRS.2002.1007892
Web of Science® Google Scholar
4 Xing C., Steady-State Analysis of Power Systems, 2007, 262, 3rd edition, Chia Electric Power Press.
Google Scholar
5 Lin W.-M. and Teng J.-H., Three-phase distribution network fast-decoupled power flow solutions, International Journal of Electrical Power and Energy System. (2000) 22, no. 5, 375–380, https://doi.org/10.1016/S0142-0615(00)00002-8, 2-s2.0-0033893503.
10.1016/S0142-0615(00)00002-8
Web of Science® Google Scholar
6 da Costa V. M., de Oliveira M. L., and Guedes M. R., Developments in the analysis of unbalanced three-phase power flow solutions, International Journal of Electrical Power and Energy Systems. (2007) 29, no. 2, 175–182, https://doi.org/10.1016/j.ijepes.2006.06.005, 2-s2.0-33751402363.
10.1016/j.ijepes.2006.06.005
Web of Science® Google Scholar
7 Song Y., Li X., and Cai W., Adaptive and fault-tolerant reactive power compensation in power systems via multilevel STATCOMs, International Journal of Innovative Computing, Information and Control. (2013) 9, no. 8, 3403–3413, 2-s2.0-84880084431.
Google Scholar
8 Nlu D. and Wei Y., A novel social-environmental-economic dispatch model for thermal/wind power generation and application, International Journal of Innovative Computing, Information and Control. (2013) 9, no. 7, 3005–3014, 2-s2.0-84880049637.
Google Scholar
9 Lo K. L. and Zhang C., Decomposed three-phase power flow solution using the sequence component frame, IEE Proceedings C: Generation Transmission and Distribution. (1993) 140, no. 3, 181–188, https://doi.org/10.1049/ip-c.1993.0028, 2-s2.0-0027599292.
10.1049/ip-c.1993.0028
Web of Science® Google Scholar
10 Abdel-Akher M., Nor K. M., and Rashid A. H. A., Improved three-phase power-flow methods using sequence components, IEEE Transactions on Power Systems. (2005) 20, no. 3, 1389–1397, https://doi.org/10.1109/TPWRS.2005.851933, 2-s2.0-24944537135.
10.1109/TPWRS.2005.851933
Web of Science® Google Scholar
11 Ngamroo I., Dynamic events analysis of Thailand and Malaysia power systems by discrete wavelet decomposition and short term fourier transform based on GPS synchronized phasor data, International Journal of Innovative Computing, Information and Control. (2013) 9, no. 5, 2203–2228, 2-s2.0-84877803383.
Google Scholar
12 Chen T. and Yang N., Loop frame of reference based three-phase power flow for unbalanced radial distribution systems, Electric Power Systems Research. (2010) 80, no. 7, 799–806, https://doi.org/10.1016/j.epsr.2009.12.006, 2-s2.0-77950863576.
10.1016/j.epsr.2009.12.006
Web of Science® Google Scholar
13 Garcia P. A. N., Pereira J. L. R., Carneiro S., and Da Costa V. M., Three-phase power flow calculations using the current injection method, IEEE Transactions on Power Systems. (2000) 15, no. 2, 508–514, https://doi.org/10.1109/59.867133, 2-s2.0-0034186739.
10.1109/59.867133
Web of Science® Google Scholar
14 Garcia P. A. N., Pereira J. L. R., CarneiroS.Jr., Vinagre M. P., and Gomes F. V., Improvements in the representation of PV buses on three-phase distribution power flow, IEEE Transactions on Power Delivery. (2004) 19, no. 2, 894–896, https://doi.org/10.1109/TPWRD.2003.820414, 2-s2.0-1942504119.
10.1109/TPWRD.2003.820414
Web of Science® Google Scholar
15 Ferreira C. A. and Da Costa V. M., A second order power flow based on current injection equations, International Journal of Electrical Power and Energy Systems. (2005) 27, no. 4, 254–263, https://doi.org/10.1016/j.ijepes.2004.10.005, 2-s2.0-14844311254.
10.1016/j.ijepes.2004.10.005
Web of Science® Google Scholar
16 da Costa V. M., Martins N., and Pereira J. L. R., Developments in the newton raphson power flow formulation based on current injections, IEEE Transactions on Power Systems. (1999) 14, no. 4, 1320–1326, https://doi.org/10.1109/59.801891, 2-s2.0-0033221709.
10.1109/59.801891
Web of Science® Google Scholar
17 Kamel S., Abdel-Akher M., and Jurado F., Improved NR current injection load flow using power mismatch representation of PV bus, International Journal of Electrical Power and Energy Systems. (2013) 53, no. 1, 64–68, https://doi.org/10.1016/j.ijepes.2013.03.039, 2-s2.0-84877771061.
10.1016/j.ijepes.2013.03.039
Web of Science® Google Scholar
18 Iwamoto S. and Tamura Y., A load flow calculation method for ill-conditioned power systems, IEEE Transactions on Power Apparatus and Systems. (1979) 100, no. 4, 1736–1743, 2-s2.0-0018285742, https://doi.org/10.1109/TPAS.1981.316511.
10.1109/TPAS.1981.316511
Web of Science® Google Scholar

Citing Literature

All articles

Improvement of Power Flow Calculation with Optimization Factor Based on Current Injection Method

Abstract

1. Introduction