Volume 2014, Issue 1 402194

Research Article

Open Access

Dynamical Analysis of a Plateau Pika with Cross-Diffusion under Contraception Control

Xiaoyan Wang

orcid.org/0000-0002-6870-6048

School of Information and Communication Engineering, North University of China, Shanxi, Taiyuan 030051, China nuc.edu.cn

Search for more papers by this author

Junyuan Yang,

Corresponding Author

Junyuan Yang

[email protected]

orcid.org/0000-0002-5825-3364

Department of Applied Mathematics, Yuncheng University, Shanxi, Yuncheng 044000, China ycu.edu.cn

Search for more papers by this author

Fengqin Zhang,

Fengqin Zhang

Department of Applied Mathematics, Yuncheng University, Shanxi, Yuncheng 044000, China ycu.edu.cn

Search for more papers by this author

Xiaoyan Wang,

Xiaoyan Wang

orcid.org/0000-0002-6870-6048

School of Information and Communication Engineering, North University of China, Shanxi, Taiyuan 030051, China nuc.edu.cn

Search for more papers by this author

Junyuan Yang,

Corresponding Author

Junyuan Yang

[email protected]

orcid.org/0000-0002-5825-3364

Department of Applied Mathematics, Yuncheng University, Shanxi, Yuncheng 044000, China ycu.edu.cn

Search for more papers by this author

Fengqin Zhang,

Fengqin Zhang

Department of Applied Mathematics, Yuncheng University, Shanxi, Yuncheng 044000, China ycu.edu.cn

Search for more papers by this author

First published: 18 February 2014

https://doi.org/10.1155/2014/402194

Academic Editor: Seenith Sivasundaram

Share a link

Email
Wechat
Bluesky

Abstract

A plateau pika model with spatial cross-diffusion is investigated. By analyzing the corresponding characteristic equations, the local stability of an coexistence steady state is discussed when d₂₁ is small enough. However, when d₂₁ is large enough, the model shows Turing bifurcation if B² − 4AC > 0. Furthermore, it is proved that if, R > R₀, βK > d and cross-diffusion rates are zero, the positive coexistence steady state is globally asymptotically stable. A nonconstant positive solution bifurcates from the coexistent steady state by the Leray-Schauder degree theory. Numerical simulations are carried out to illustrate the main results.

1. Introduction

Plateau pika (Ochotona curzoniae) is a species of small mammals in the Ochotonidae. According to the studies [1–4], it is found that the plateau pika’s burrows are the primary homes to a wide variety of small birds and lizards since Qinghai-Tibet area owns the treeless environment and also minimize soil erosion for the suitable number of plateau pikas, enhance the ability of soil to absorb precipitation, contribute to nutrient cycling, and create microhabitats resulting in increased plant species richness; it serves as the main prey for most of the predatory animals on the plateau. Hence, the plateau pika is a keystone species in Qinghai-Tibet plateau. Since people overgraze and climate becomes warm, which makes the alpine meadow degrade seriously and provides the suitable environment for the plateau pika, multiplication of plateau pika is overabundance. According to the statistics data [1–4], there exists the huge number of the plateau pikas in this areas, and it threatens the forage that could otherwise be utilized by the livestock and the huge number of burrows results in soil erosion, vegetation disturbances, and the individuals who ride horses across the grasslands hazard. Hence plateau pika has been listed as a pest for the Chinese Government.

During the recent years, the various methods are applied to manage the number of plateau pikas. In the first stage, since people are lacking enough understanding about the plateau pika, they directly poisoned the plateau pike with botulin of models C and D. The people considered the plateau pika as rodent; in fact, pikas belong to lagomorphs and not to rodents. From the first paragraph, plateau pike is keystone species, whose elimination or major decimation from an ecosystem would have a greater average effect on other species’ populations or ecosystem processes. Hence, plateau pika contributes to maintaining the biodiversity in Qinghai-Tibet plateau [1, 2]. Obviously it does not work for the people to kill the plateau pika with any chemical sterilant. For the balance of the ecology and long-term development, immunocontraception has been used to manage plateau pika. Immunocontraception is different from the traditional method to manage the plateau pika. It aims to reduce the birth rate of the plateau pika and increase the death rate of the plateau pika. This control method can make the plateau pika be maintained at a low or suitable level for a long period. If we carry out the control method at the breeding season, the number of plateau pikas may be controlled at a desirable level. Several mathematical models describing the plateau pika under sterile control have been employed and analyzed. Dobson et al. [5] show that family structure has a strong influence on pika gene dynamics even though mating patterns of plateau pikas are variable. Smith and Cheeseman [6] show that a permanent contraceptive can give the chances of disease eradication which were very similar to that of lethal control. Burkey and Stenseth [7] discuss the effects of resource patchiness and the effects of a seasonal environment on the population dynamics of the herbivore species. Liu et al. [8] proposed a discrete model incorporating the sterile and the lethal control. In this model, the reproductive number plays a key role in impacting the dynamics of the model. Liu and Li [9] build a mathematical model to discuss the single species population under contraceptive control and lethal control. They studied the stability of the equilibrium of the model. Liu et al. [10] use a cellular-automata model to investigate the influence of grazing on dynamics of plateau pika population. The dispersal dimension depends on the meadow degradation.

Animal populations may not be distributed randomly in space but exhibit spatial patterns, and plateau pika is not exception. Plateau pika spatial distribution in the plateau is directly affected by individual interactions and interspecific interactions. Plateau pika dispersing is a natural phenomenon. Pikas from the different plateaus often contact and move towards favorable habitats due to climate, food, predators, and so on. This phenomena can employ random diffusion combined with directed movement upward along environmental gradients. Many interesting papers investigating species diffusion have been discussed by many authors. In [11], there is no difference in the average distance dispersed by the male and female sexes, since the costs and benefits of dispersal do not differ between males and females in the species. Dispersal movements in [12] result in equalization of density among pika families, if competition for environmental resources influenced dispersal. Wang and Li [13, 14] discuss the positive stationary problems in population cross-diffusion using the bifurcation theory. Pang and Wang [15] consider the positive solution for the population cross-diffusion. Cross-diffusion inducing the Turing bifurcation can also be studied by [16–20]. One can refer to [13–29] and references therein for more details. Although there are many references which discussed the population diffusion and cross-diffusion, plateau pika population diffusion or cross-diffusion under contraception still remains a problem. At the best of our knowledge as the authors known, we do not find any relative report or study until now. Hence pikas diffusion is very interesting and is worth studying.

This paper is organized as follows. Section 2 introduces a plateau pika model under contraceptive control and lethal control. In Section 3, local stability of the positive steady state is studied. In Section 4, we obtain persistence of the system. In Section 5, global stability and existence of the nonconstant steady state are investigated. The conclusion is given and some simulations to illustrate the theoretical results.

2. The Model Formulation

For the single species model under contraceptive control and lethal control, it is mentioned in the introduction [9]. The total population is divided into two classes: female plateau pika sterile female plateau pika. The numbers of individuals in these classes at time t are denoted, respectively, by F(t) and S(t). The population density decreases due to the control; a compensatory reaction from all or part of the population occurs due to increased access to resources. In this model, a fraction of the population is implemented by immunocontraception; they separate the female population into two contributions explicitly; one (the birth rate B) is norm and the other (the death rate D) is immunocontraception. They assume that the immunocontraception just impacts the birth rate B. Hence birth rate B and death rate D can be expressed as

()

This model is described as follows:

()

Here, b is the birth rate, d is mortality rate, the intrinsic growth rate r = b − d, μ is the death rate due to chemical sterilant, K denotes the carrying capacity, and β is efficient transmitted rate from female plateau pika to sterile female plateau pika though the contact. For the biological meaning of the model, b − d > 0 holds in the procession. They obtain the following lemma. Define R = b − d − μ, R₀ = (b − d)(μ + d)/βK, and then it is easy to compute E^** = (F^*, S^*) = ((d + μ)/β, (R − R₀)K/(b − d + βK)).

Lemma 1. When R > R₀ and βK > d, the positive equilibrium E^** is globally asymptotically stable.

In this paper, we are concerned with the effect of the cross-diffusion under the contraceptive control and lethal control. The transmission dynamics of infection are governed by the following differential equations:

()

where fertile female plateau pika (F) densities and sterile female plateau pika (S) densities are denoted at location x, and time t, respectively. Ω is a fix bounded domain Ω ⊂ ℝ^N with smooth boundary ∂Ω, ν is the outward unit normal vector of the boundary ∂Ω, Δ is the Laplacian operator, and positive constants d₁, d₂ are the diffusive coefficients which denote the nature dispersive force of movement of the fertile female, and sterile female, respectively. The nonnegative constants d₁₂ and d₂₁ which mean the tendency that the sterile female (fertile female) keeps away from the fertile female (sterile female) are usually referred as cross-diffusion pressure. d is the remove rate from free virus. For t ≥ 0, x ∈ Ω, with homogeneous Neumann boundary conditions

()

and initial conditions

()

The boundary conditions in (4) imply that the populations do not move across the boundary ∂Ω. By the maximum principle, both F(x, t) and S(x, t) are positive for

and t ∈ [0, T_max⁡). Again by the maximum principle, F and S are bounded on

. Therefore, the time existence interval can extend to ∞ by the standard theory for semilinear parabolic systems. The other parameters are similarly well defined as [9]. In addition, the model (3) is well posed that is, there exists a unique classical solution of (3).

For the convenience to study the dynamics of (3), we first give the classical results for the elliptic equation.

Lemma 2 (Harnack inequality [30]). Assume that c ∈ C(Ω) and let be a positive solution to

()

Then there exists a positive constant C_* = C_*(∥c∥_∞) such that

Lemma 3 (maximum principle [25]). Suppose that . Assume that satisfies

()

, then g(x₀, w) ≥ 0(≤0).

3. Stability of Steady States

In this section, first we cite Lemma 1 and find that (3) still has a positive steady state w^* = (F^*, S^*) if R > R₀ and βK > d. Second we discuss the linearized problem of (3) at w^* = (F^*, S^*). For simplicity, we denote

()

Then problem (3) can be written as

()

Let 0 = μ₁ < μ₂ < ⋯ be the eigenvalues of the operator −Δ on Ω with the homogeneous Neumann boundary conditions, and let E(μ_i) be the eigenspace corresponding to μ_i in C¹(Ω). Let 𝒳 = (C¹(Ω)) ², {ϕ_ij, j = 1, …, dim⁡E(μ_i)} be an orthonormal basis of E(μ_i), and 𝒳_ij = {cϕ_ij∣c ∈ ℝ²}. Then

()

Let

()

where

()

The linearization of system (3) at w^* is of the form w_t = ℒw, where

. For each i ≥ 1, 𝒳_i is invariant under the operator ℒ, and λ is an eigenvalue of ℒ if and only if it is an eigenvalue of the matrix −μ_iΦ_w(w^*) + Ψ(w^*) for some i ≥ 1, in which case, there is an eigenvector in 𝒳_i.

By a direct calculation, we have

()

with

()

thus the characteristic equation of the matrix ℒ is

()

Note, when the system (3) has no diffusion effects, the stability of coexistence equilibrium was discussed by [9]. There exists a sufficient condition R > R₀, βK > d for proving the existence and the global stability of the coexistence steady state.

Case 1. Consider d₁₂ = d₂₁ = 0.

In this case, it is easy to get the characteristic equation of the coexistence steady state w^* as follows:

()

where ℒ₁ is the linear operator ℒ when d₂₁ = d₁₂ = 0 and

()

It is obviously that trace(ℒ₁) < 0 and det⁡(ℒ₁) > 0. Thus, the real part of the characteristic roots of ℒ₁ is less than 0. Therefore, we have the following theorem.

Theorem 4. If R > R₀, βK > d, and d₁₂ = d₂₁ = 0, then the positive coexistence steady state w^* of (3) is locally asymptotically stable. In this case, Turing instability does not occur for (3).

Case 2. Consider d₁₂d₂₁ ≠ 0.

From the computation and notations, the trace of ℒ is less than 0, A > 0, and C > 0. Since μ_i ≥ 0, a necessary condition for w^* of (3) becoming unstable is that det⁡ℒ for some μ_i is less than 0. Since μ_i is always nonnegative, the symmetric axis of the curve Ax² − Bx + C must be at the right half plane, so B must be positive; that is, d₂₁ > βd₁₂S^* + d₂(b − d)/K. At the same time, the equation of Ax² − Bx + C = 0 must have two positive roots; then B² − 4AC > 0 must be satisfied for the instability of the positive coexistence steady state. Hence, has two positive roots

()

It is easy to know that, if μ¹ < μ_i < μ² for some μ_i ≥ 0, then det⁡{ℒ} < 0. Therefore, we have the following theorem.

Theorem 5. Assume R > R₀, and βK > d hold. If d₂₁ > βd₁₂S^* + d₂(b − d)/K, and B² − 4AC > 0, then the positive coexistent steady state w^* is unstable and (3) exhibits Turing bifurcation provided that, for some μ¹ < μ_i < μ², i = 1,2, ….

Remark 6. From the definition of B, it is easy to get the following.

(i)
When d₂₁ = 0, d₁₂ ≠ 0, B = −d₂(b − d)F^*/K − d₁₂βS^*F^* < 0. Then Turing bifurcation does not appear in (3).
(ii)
When d₁₂ = 0, d₂₁ ≠ 0 or d₁₂ ≠ 0, d₂₁ ≠ 0, and d₂₁ is large enough, which make B > 0 and B² − 4AC > 0, there exists some μ_i > 0, such that μ¹ < μ_i < μ². Under this situation, w^* is unstable while w^* is stable for the ODE situation. Hence, Turing bifurcation may emerge in (3) if the cross-diffusion coefficients of the sterile female plateau pika d₂₁ is large enough.

4. A Priori Estimation

In this section, we will be interested primarily in steady state of (3). Now we first give a priori estimate for positive solutions to the elliptic system

()

which is the corresponding steady state of (3).

In the following, we will discuss the upper bounds and the lower bounds by using Lemma 2 and Lemma 3. By the regularity theory for elliptic equations, it is easy to know that the positive solution of (19) is in .

Theorem 7. Assume that d₁₂/d₁, d₁/d₂, d₁₂/d₂, d₂₁/d₂ are bounded; then there exist positive constants C_i, i = 1,2, such that the positive solution w of (19) satisfies

()

Proof. For using the Lemma 3, we set ϕ = d₁F + d₁₂SF, ψ = d₁F + d₂S + (d₁₂ + d₂₁)SF then elliptic equation (19) becomes

()

Let such that . By the first equation of (19) and Lemma 3, we have F(x₁) ≤ K, and S(x₁) ≤ K. Then, by the denotation of ϕ, we have

()

Similarly, let

such that

. By the second equation of (19) and Lemma 3, we have F(x₂) ≤ K, S(x₂) ≤ K. Then, by the denotation of ψ, we have

()

The proof is completely finished.

From Theorem 7, the population of plateau pika for (3) is boundary. Since the maximum capability carrying has limitation, the population of the plateau pika for (3) can not tend infinity. For proving the persistence of the plateau pika, we can obtain the following theorem.

Theorem 8. Assume that d₁₂/d₁, d₁/d₂, (d₁₂ + d₂₁)/d₂ are bounded; then there exist positive constants c_i, i = 1,2, such that the positive solution w of (19) satisfies

()

Proof. Since

()

By Lemma 2, there exists a constant

such that

. Hence, we have

()

By integrating the second equation of (19) in Ω, we have

()

which implies that there exists x₃, such that βF(x₃)−(μ + d) = 0. Then F(x₃) = (μ + d)/β. By combining with (26) yields that

()

Now we need to estimate the positive lower bound of S. Suppose, on the contrary, that does not hold. Define . Then there exists a sequence with (d_1n, d_2n, d_12n, d_21n)∈[d, ∞)×[d, ∞)×(0, ∞)×(0, ∞) such that the corresponding positive solutions w_n of (19) satisfy

()

Using

and the second equation (21) yields

()

By Lemma 2, there exists a constant

such that

()

Similarly, we have the following relation between max⁡S and min⁡S

()

It follows from (30) and (33) that

()

There exists a subsequence of w_n, which is denoted by w_nk, and two nonnegative functions

, such that

as k → ∞. Combining (30) and (34), one gets

. By the L^p regularity theory of elliptic equations and the Sobolev embedding theorem, for some α ∈ (0,1), the

norm of w_nk is uniformly bounded with respect to k. Then, taking the limits for the first equation of (29), we have

()

Therefore,

; otherwise

, which is obviously impossible. So,

Taking the limit and integrating the second equation of (29), we have

()

Therefore,

; that is, R = R₀, which is a contradiction with the existence of the positive coexistence steady state.

By Theorems 7 and 8, we can define a set

()

where c_i, C_i = 1,2 is defined by Theorems 7 and 8. It is easy to get the set ℬ(c) which is invariant set for (3). We can discuss the dynamics of (3) in this set ℬ.

5. Global Stability of the Steady State and the Existence of Nonconstant Positive Solution

In order to discuss the existence of nonconstant positive solution of (3), we first prove the global stability of the coexistence equilibrium w^*, when the cross-diffusion coefficients are zero. Then there is no nonconstant solution with respect to elliptic equation (19). We obtain the following theorem.

Theorem 9. Assume R > R₀, βK > d. The positive coexistence equilibrium of (3) is globally asymptotic stable when the cross-diffusion coefficients are zero; that is, (19) has no nonconstant positive solution.

Proof. Let f^* = 1/|Ω|∫_Ω f dx for any f ∈ L¹(Ω). We denote the Lyapunov function as follows:

()

We derivative V with t along the system (3) and get

()

We choose α = ((b − d) + βK)/βK and substitute it into (39); thus

()

Let M be the largest invariant set of {dV(t)/dt = 0}, that, is invariant with respect to (3). It is easy to get that dV(t)/dt = 0 if and only if F = F^*. We show that M consists of only the coexistence equilibrium w^*. Since M is invariant, we have dF(t)/dt = 0 and ΔF = 0 in M. Then from the first equation of (3), it holds that

()

We must have S(t, x) = S^* for all t, x. Thus, the set M consists of only the endemic equilibrium w^*. This completes the proof.

In the following, we consider that the cross-diffusion induces the nonconstant solution for (19). The Leray-Schauder degree theory is a good method to establish the existence of stationary patterns of (19). For the convenience, we define a positive cone as

()

In order to use Leray-Schauder degree, we must revise system (19) as a fixed problem. From the definition of elliptic operator Δ, we have

()

Hence, if L(·) ≠ 0 on ∂ℬ, then the Leray-Schauder degree deg⁡(L(·), 0, ℬ) is well defined. By a direct computation, it is easy to obtain

()

Thus, the index of the operator L at coexistence steady state is defined as the following formula:

()

if D_wL(w^*) is invertible τ which is considered as the total number of eigenvalues of D_wL(w^*) with negative real parts (counting multiplicities). Since μ_i is the characteristic eigenvalue of the operator −Δ, the eigenvalue of D_wL(w^*) is determined by the following matrix:

()

For the denotational convenience, we denote

()

According to the references [15], we have the following lemma.

Lemma 10. If G(μ_i) ≠ 0, then the number of negative eigenvalues of D_wL(w^*) on X_ij is odd if and only if G(μ_i) < 0, for each 1 ≤ j ≤ dim⁡E(μ_i). In addition,

()

Recall that det⁡Φ_w(w^*) > 0, and so do

. Then the sign of G(μ) is determined by

which is equivalent to det⁡{−μΦ_w(w^*) + Ψ_w(w^*)} since the matrix μΦ_w(w^*) − Ψ_w(w^*) is 2 × 2. From the remark of Theorem 5, if d₂₁ is large enough, the determination

()

may be less than 0.

In the following, we consider how the cross-diffusion coefficient d₂₁ impacts the determination. By the definitions of A, B, and C in Section 3, and 𝒜(μ, d₂₁), one obtains

()

The two roots of 𝒜(μ, d₂₁) = 0 are defined by

and

, respectively. Combining the definition of the upper limits, we have the following lemma.

Lemma 11. Assume R > R₀, βK > d. Then the two roots and of 𝒜(μ, d₂₁) are real and satisfy the following limits for some such that, for all the ,

()

Next we will discuss the existence of nonconstant positive solution of (19) with respect to the cross-diffusion coefficient d₂₁.

Theorem 12. Assume that the other parameters in (19) are fixed except d₂₁, and R > R₀, βK > d hold. is given by the limit in (51). If for some n ≠ 1, and the sum is odd, then there exists a positive constant , such that, if , there exists at least one nonconstant positive solution which bifurcates from the coexistence steady state of (19).

Proof. Due to Lemma 11, there exists a positive , if ; then there exists two positive roots for 𝒜(μ, d₂₁) and

()

In order to prove the result, we use the contradict method. We assert that the result is not true. By using the homotopy argument, we can derive a contradiction.

For t ∈ [0,1], define

()

and consider the problem

()

Then w is a nonconstant positive solution of (54) for any t ∈ [0,1]. By the definition of L(w), for any t ∈ [0,1], w is a positive solution of (30) if and only if

()

It is easy to check that L(1; w) = L(w), Theorem 9 indicates that L(0; w) = 0 has only the positive solution w^* in X₊. Dividing L(t; w) with respect to w, we have

()

In particular,

()

where Φ_w(0; w^*) = diag⁡(d₁, d₂), Φ_w(1; w^*) = Φ_w(w^*). Then D_wL(1; w^*) = D_wL(w^*).

By the definition of G(μ), 𝒜(μ, d₂₁) and Lemma 10, for t = 1, we have

()

And note that 0 is not an eigenvalue of the matrix

for all i ≥ 0, and

()

If σ_n is odd, it follows from Lemma 10 that

()

Note that H(μ) > 0 when t = 0 for Theorem 9. Thus we have

()

In addition, L(t; w) ≠ 0 on ∂ℬ(c) for all t ∈ [01] by Theorems 7 and 8, while we use the homotopy invariance of the topological degree to obtain

()

It is easy to know that w^* is the root of both L(1; w) and L(0; w) in ℬ(c). Combining (60) and (61), we have

()

which is contradiction to (62). This completes the proof.

6. Simulation and Discussion

We have formulated a plateau pika model with cross-diffusion. By Lemma 1, there is a unique positive coexistent steady state of (3) when R > R₀, and βK > d. As the sterile female cross-diffusion is small enough, (3) does not exhibit Turing bifurcation. However, if the cross-diffusion rate is large enough, Turing bifurcation emerges in coexistence steady state. The system (3) is persistence and bound under some boundary conditions. If the cross-diffusion rates d₁₂, d₂₁ are both zeros, the coexistence steady state is globally stable by using the Lyapunov functions. As the pressure from the sterile female plateau pika to the female plateau pika is large enough, a nonconstant steady state solution will bifurcate from the positive steady state by using Leray-Schauder degree theory. From the biological view, the sterile female plateau pika giving the pressure to the the female plateau pika plays an important role in controlling the population of plateau pika in Qinghai-Tibet area, since the plateau pika is one keystone species of plateau. Blending the population of plateau pika to eradicate is not realistic and may disturb the biological balance in the plateau. We should carry out the measures to control the population of the plateau pika tending some level, which is not harmful to the plateau, and is also benefitcial to persisting the biological balance. From the mathematical view, it is better for

where

is the level for the persisting ecological cycle. Note that N^* = F^* + S^*; it is easy to get the following formula though a direct computation:

()

To understand how the total population of the plateau pika can be lowered, we consider its elasticity with respect to the key parameters that can be affected by control measures. In particular, we define elasticity of quantity Q with respect to parameter ν as

()

We can compute the following elasticity quantities:

()

Assume that b > d, βK > d satisfies the existence condition of the positive coexistence steady state. We note that

is positive, while

is always negative. Hence, if we want to control the population of plateau pika, we should decrease the birth rate, death rate, and capability, while increasing the transmitted rate for themselves from the theoretical view. However, the death rate d and capability carrying K are harder controlled than the birth rate b and transmitted rate β. For the specific control measure, increasing the transmitted rate and decreasing the birth rate are possible. Hence the contraception is a better method for this. For the formula of the elasticity of N^* with respect to b and β, if the impact of birth rate is larger than the transmitted rate, β must satisfy β² − Kβ + d < 0; thus K² > 4d. Hence the protection of environment for the plateau pika is also important.

We can illustrate the theoretical results through two simulatinon examples. Set b = 0.749, d = 0.3311, K = 100, β = 0.01, μ = 0.01, d₁ = 0.2, d₂ = 0.3, d₁₂ = 0, d₂₁ = 0. It is easy to get that R = 0.4079 > R₀ = 0.425 and βK = 1 > d = 0.3311 satisfy the conditions of Lemma 1. System (3) with above coefficients has a unique positive steady state w^* = (34.11,18.7146). By Theorem 9, we see that the coexistence steady state w^* of (3) is globally stable.

Numerical simulation illustrates our result (see Figure 1). Then we let d₁₂ = 0.01, d₂₁ = 0, and other parameters be the same as Figure 1. System (3) with above coefficients still has a unique positive steady state w^* which is the same as Figure 1. By Theorem 5, we see that the coexistence steady state w^* of problem (3) is locally stable. Numerical simulation illustrates our results (see Figure 2). We can also know that the pressure from the female plateau pika to sterile female plateau pika diffusion d₁₂ does not change the stability of system (3). However, we also find that the diffusion can advance the time for both the female plateau pika and the sterile female plateau pika to arrive at the coexistence steady state.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Plateau pika coexistence steady state w^* with initial conditions F(x, 0) = F₀(x) = 1, S(x, 0) = S₀(x) = 0.5.

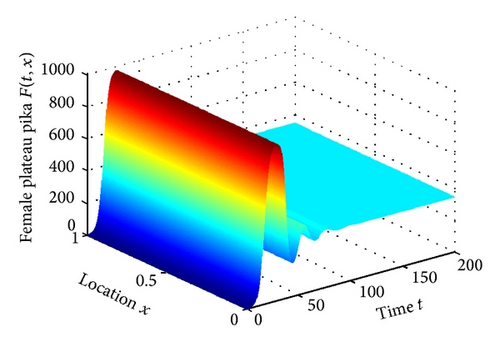
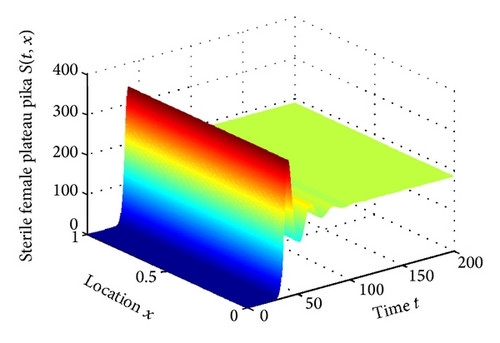
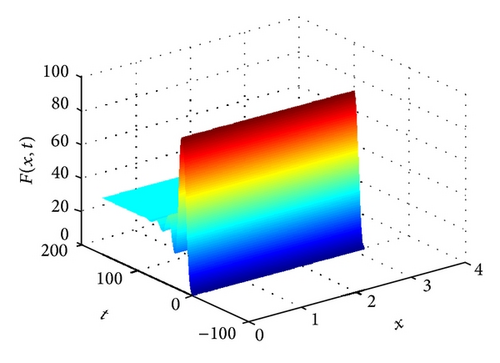
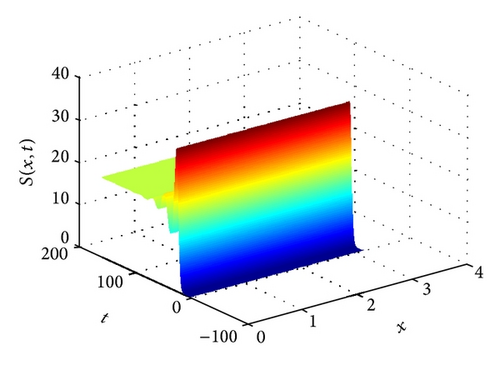
For the management of the application, larger β resulted in small number of the plateau pikas. Hence we should try our best to combine a powerful contraception method with some additional measures to control the plateau pikas. In addition, the diffusion can advance the time for both the female plateau pika and the sterile female plateau pika to arrive at the coexistence steady state. Increasing the cross-diffusion coefficients can rich the dynamics of the model and enhance the difficulty of the control. The system may show the Turing bifurcation.

Unfortunately, we are unable yet to study global stability of coexistence steady state w^* when d₁₂ ≠ 0, d₂₁ = 0. In addition, we do not study the dynamics of (3) when B² − 4AC = 0. In this case det⁡ℒ = 0, the system may exhibit steady state bifurcation.

Conflict of Interests

The authors declare that they have no conflict of interests.

Acknowledgments

This study is supported by the NSF of China (61203228, 61275120, and 11371313), Mathematical Tianyuan Foundation (11226258), the Young Sciences Foundation of Shanxi (2011021001-1), the Natural Science Foundation of Shanxi Province (2013011002-5), program for the Outstanding Innovative Teams of Higher Learning Institutions of Shanxi, and the “131” talents.

References

1 Smith A. T. and Foggin J. M., The plateau pika (Ochotona curzoniae) is a keystone species for biodiversity on the Tibetan plateau, Animal Conservation. (1999) 2, no. 4, 235–240, https://doi.org/10.1111/j.1469-1795.1999.tb00069.x, 2-s2.0-0002641491.
10.1111/j.1469-1795.1999.tb00069.x
Web of Science® Google Scholar
2 Lai C. H. and Smith A. T., Keystone status of plateau pikas (Ochotona curzoniae): effect of control on biodiversity of native birds, Biodiversity and Conservation. (2003) 12, no. 9, 1901–1912, 2-s2.0-0037523275, https://doi.org/10.1023/A:1024161409110.
10.1023/A:1024161409110
Web of Science® Google Scholar
3 Wang C., He H., Li M., Lei F., Root J. J., Wu Y., and Qin J., Parasite species associated with wild plateau pika (Ochotona curzoniae) in southeastern Qinghai Province, China, Journal of Wildlife Diseases. (2009) 45, no. 2, 288–294, https://doi.org/10.7589/0090-3558-45.2.288, 2-s2.0-67649963648.
10.7589/0090-3558-45.2.288
PubMed Web of Science® Google Scholar
4 Wang Z. L., Chen Y., Yang J., Chen W. J., Zhang Y. M., and Zhao X. Q., Behavioral mechanisms of male sterilization on plateau pika in the Qinghai-Tibet plateau, Behavioural Processes. (2012) 89, no. 3, 278–285, 2-s2.0-84857139361, https://doi.org/10.1016/j.beproc.2011.12.009.
10.1016/j.beproc.2011.12.009
PubMed Web of Science® Google Scholar
5 Dobson F. S., Smith A. T., and Gao W. X., The mating system and gene dynamics of plateau pikas, Behavioural Processes. (2000) 51, no. 1–3, 101–110, 2-s2.0-0034609719, https://doi.org/10.1016/S0376-6357(00)00122-4.
10.1016/S0376-6357(00)00122-4
CAS PubMed Web of Science® Google Scholar
6 Smith G. C. and Cheeseman C. L., A mathematical model for the control of diseases in wildlife populations: culling, vaccination and fertility control, Ecological Modelling. (2002) 150, no. 1-2, 45–53, 2-s2.0-0037090950, https://doi.org/10.1016/S0304-3800(01)00471-9.
10.1016/S0304-3800(01)00471-9
Web of Science® Google Scholar
7 Burkey T. V. and Stenseth N. C., Population dynamics of territorial species in seasonal and patchy environments, Oikos. (1994) 69, no. 1, 47–53, 2-s2.0-0028176225.
10.2307/3545282
Web of Science® Google Scholar
8 Liu H. W., Jin Z., Chen Y. M., and Zhang F. Q., Population dynamics of plateau pika under lethalcontrol and contraception control, Advances in Difference Equations. (2012) 2012, no. article 29, 13, https://doi.org/10.1186/1687-1847-2012-29.
10.1186/1687-1847-2012-29
PubMed Google Scholar
9 Liu H. W. and Li Q. Y., Model of single-species population under contraceptive control and lethal control, Mathematics in Practice and Theory. (2009) 39, no. 15, 104–107.
Google Scholar
10 Liu H. W., Zhou L., Liu W., and Zhou H. K., Using a cellular-automata model to investigate the effects of grazing on plateau pika population dynamics, International Journal of Biomathematics. (2011) 4, no. 3, 275–287, https://doi.org/10.1142/S179352451100126X, MR2845200, ZBL1251.92043.
10.1142/S179352451100126X
Web of Science® Google Scholar
11 Jessie M. Z. and David S. H., Polygynandry and even-sexed dispersal in a population of collared pikas, Ochotona collaris, Animal Behaviour. (2012) 83, no. 4, 1075–1082, 2-s2.0-84858752645, https://doi.org/10.1016/j.anbehav.2012.01.038.
10.1016/j.anbehav.2012.01.038
Web of Science® Google Scholar
12 Dobson F. S., Smith A. T., and Gao W. X., Social and ecological influences on dispersal and philopatry in the plateau pika, Behavioral Ecology. (1998) 9, no. 6, 622–635, 2-s2.0-0031729804.
10.1093/beheco/9.6.622
PubMed Web of Science® Google Scholar
13 Wang Y.-X. and Li W.-T., Effects of cross-diffusion and heterogeneous environment on positive steady states of a prey-predator system, Nonlinear Analysis: Real World Applications. (2013) 14, no. 2, 1235–1246, https://doi.org/10.1016/j.nonrwa.2012.09.015, MR2991149, ZBL1261.35019.
10.1016/j.nonrwa.2012.09.015
Web of Science® Google Scholar
14 Wang Y.-X. and Li W.-T., Effect of cross-diffusion on the stationary problem of a diffusive competition model with a protection zone, Nonlinear Analysis: Real World Applications. (2013) 14, no. 1, 224–245, https://doi.org/10.1016/j.nonrwa.2012.06.001, MR2969831, ZBL06118945.
10.1016/j.nonrwa.2012.06.001
Web of Science® Google Scholar
15 Pang P. Y. H. and Wang M. X., Existence of global solutions for a three-species predator-prey model with cross-diffusion, Mathematische Nachrichten. (2008) 281, no. 4, 555–560, https://doi.org/10.1002/mana.200510624, MR2404298, ZBL1139.35052.
10.1002/mana.200510624
Web of Science® Google Scholar
16 Liu J., Zhou H., and Zhang L., Cross-diffusion induced Turing patterns in a sex-structured predator-prey model, International Journal of Biomathematics. (2012) 5, no. 4, 23, 1250016, https://doi.org/10.1142/S179352451100157X, MR2926078.
10.1142/S179352451100157X
Web of Science® Google Scholar
17 Hu G.-P. and Li X.-L., Turing patterns of a predator-prey model with a modified Leslie-Gower term and cross-diffusions, International Journal of Biomathematics. (2012) 5, no. 6, 17, 1250060, https://doi.org/10.1142/S179352451250060X, MR2969659.
10.1142/S179352451250060X
Web of Science® Google Scholar
18 Tian C. R., Lin Z. G., and Pedersen M., Instability induced by cross-diffusion in reaction-diffusion systems, Nonlinear Analysis: Real World Applications. (2010) 11, no. 2, 1036–1045, https://doi.org/10.1016/j.nonrwa.2009.01.043, MR2571274, ZBL1180.35098.
10.1016/j.nonrwa.2009.01.043
CAS Web of Science® Google Scholar
19 Gambino G., Lombardo M. C., and Sammartino M., Turing instability and traveling fronts for a nonlinear reaction-diffusion system with cross-diffusion, Mathematics and Computers in Simulation. (2012) 82, no. 6, 1112–1132, https://doi.org/10.1016/j.matcom.2011.11.004, MR2903351, ZBL06055096.
10.1016/j.matcom.2011.11.004
Web of Science® Google Scholar
20 Xie Z., Cross-diffusion induced Turing instability for a three species food chain model, Journal of Mathematical Analysis and Applications. (2012) 388, no. 1, 539–547, https://doi.org/10.1016/j.jmaa.2011.10.054, MR2869768, ZBL1243.35093.
10.1016/j.jmaa.2011.10.054
Web of Science® Google Scholar
21 Ruiz-Baier R. and Tian C., Mathematical analysis and numerical simulation of pattern formation under cross-diffusion, Nonlinear Analysis: Real World Applications. (2013) 14, no. 1, 601–612, https://doi.org/10.1016/j.nonrwa.2012.07.020, MR2969859, ZBL1263.92007.
10.1016/j.nonrwa.2012.07.020
Web of Science® Google Scholar
22 Ko W. and Ryu K., On a predator-prey system with cross diffusion representing the tendency of predators in the presence of prey species, Journal of Mathematical Analysis and Applications. (2008) 341, no. 2, 1133–1142, https://doi.org/10.1016/j.jmaa.2007.11.018, MR2398275, ZBL1160.35021.
10.1016/j.jmaa.2007.11.018
Web of Science® Google Scholar
23 Ni W.-M., Diffusion, cross-diffusion, and their spike-layer steady states, Notices of the American Mathematical Society. (1998) 45, no. 1, 9–18, MR1490535, ZBL0917.35047.
Google Scholar
24 Kolokolnikov T. and Wei J., Stability of spiky solutions in a competition model with cross-diffusion, SIAM Journal on Applied Mathematics. (2011) 71, no. 4, 1428–1457, https://doi.org/10.1137/100808381, MR2835241, ZBL1259.35018.
10.1137/100808381
Web of Science® Google Scholar
25 Lou Y. and Ni W. M., Diffusion, self-diffusion and cross-diffusion, Journal of Differential Equations. (1996) 131, no. 1, 79–131, https://doi.org/10.1006/jdeq.1996.0157.
10.1006/jdeq.1996.0157
Web of Science® Google Scholar
26 Lou Y. and Ni W.-M., Diffusion vs cross-diffusion: an elliptic approach, Journal of Differential Equations. (1999) 154, no. 1, 157–190, https://doi.org/10.1006/jdeq.1998.3559, MR1685622, ZBL0934.35040.
10.1006/jdeq.1998.3559
Web of Science® Google Scholar
27 Lou Y., Ni W.-M., and Wu Y., On the global existence of a cross-diffusion system, Discrete and Continuous Dynamical Systems. (1998) 4, no. 2, 193–203, https://doi.org/10.3934/dcds.1998.4.193, MR1616969, ZBL0960.35049.
10.3934/dcds.1998.4.193
Google Scholar
28 Tuôc P. V., Global existence of solutions to Shigesada-Kawasaki-Teramoto cross-diffusion systems on domains of arbitrary dimensions, Proceedings of the American Mathematical Society. (2007) 135, no. 12, 3933–3941, https://doi.org/10.1090/S0002-9939-07-08978-2, MR2341943.
10.1090/S0002-9939-07-08978-2
Web of Science® Google Scholar
29 Zeng X., Non-constant positive steady states of a prey-predator system with cross-diffusions, Journal of Mathematical Analysis and Applications. (2007) 332, no. 2, 989–1009, https://doi.org/10.1016/j.jmaa.2006.10.075, MR2324315, ZBL1168.35350.
10.1016/j.jmaa.2006.10.075
Web of Science® Google Scholar
30 Lin L. S., Ni W. M., and Takagi I., Large amplitude stationary solutions to a chemotaxis system, Journal of Differential Equations. (1988) 72, no. 1, 1–27, https://doi.org/10.1016/0022-0396(88)90147-7, MR929196, ZBL0676.35030.
10.1016/0022-0396(88)90147-7
Web of Science® Google Scholar

All articles

Dynamical Analysis of a Plateau Pika with Cross-Diffusion under Contraception Control

Abstract

1. Introduction

2. The Model Formulation

3. Stability of Steady States

4. A Priori Estimation

5. Global Stability of the Steady State and the Existence of Nonconstant Positive Solution

6. Simulation and Discussion

Conflict of Interests

Acknowledgments

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Dynamical Analysis of a Plateau Pika with Cross-Diffusion under Contraception Control

Abstract

1. Introduction

2. The Model Formulation

3. Stability of Steady States

4. A Priori Estimation

5. Global Stability of the Steady State and the Existence of Nonconstant Positive Solution

6. Simulation and Discussion

Conflict of Interests

Acknowledgments

References

Figures

References

Related

Information