We propose a simple, though powerful, technique for numerical solutions of the Benjamin-Ono equation. This approach is based on a global collocation method using Sinc basis functions. Some properties of the Sinc collocation method required for our subsequent development are given and utilized to reduce the computation of the Benjamin-Ono equation to a system of ordinary differential equations. The propagation of one soliton and the interaction of two solitons are used to validate our numerical method. The method is easy to implement and yields accurate results.

1. Introduction

It is well known that nonlinear partial differential equations (NPDEs) are widely used to describe complex phenomena in various fields of sciences, such as physics, biology, and chemistry.

In this paper, we consider the initial value problem for the Benjamin-Ono (BO) equation of the form

()

together with the following initial and the boundary conditions:

()

Here

is a real valued function and

denotes the Hilbert transform defined and described by [1] (amongst others):

()

where P denotes the Cauchy principal value. This equation was derived by Benjamin [2] and later by Ono [3] as a model for one-dimensional waves in deep water and it has a close relation with the famous KdV equation which models long waves in shallow water [4].

We recall that the BO equation has an infinite sequence of invariants [5], the first three of which are

()

The BO has been shown to admit rational analytical soliton solutions in x and t [6]. However, for a given arbitrary initial condition, finding analytical solutions of the BO equation becomes an intractable problem. Therefore the use of numerical methods plays an important role in the study of the dynamics of the BO equation.

James and Weideman [7] used the Fourier method which implicitly assumes the periodicity of the boundary conditions and a method based on rational approximating function to compute numerical solutions of the BO. The rational method was shown to have spectacular accuracy for solutions that do not wander too far from the origin while, for long dated solutions, the Fourier method was shown to retain superior accuracy. Miloh et al. [8] proposed an efficient pseudospectral method for the numerical solution of the weakly nonlinear Benjamin-Ono equation for arbitrary initial conditions and suggested a practical new relationship for estimating the number of solitons in terms of arbitrary initial conditions. Thomée and Vsaudeva Murthy [9] used the Crank-Nicolson approximation in time and finite difference approximations in space to solve the BO equation. They treated the nonlinear term in a standard conservative fashion and discretized the Hilbert transform by a quadrature formula which was computed efficiently using the fast Fourier transform. Recently, Boyd and Xu [10] compared three spectral methods for solving the Benjamin-Ono equation, Fourier pseudospectral, rational Christov functions, and Gaussian radial basis functions. They highlighted the advantages and the disadvantages of each numerical method. For instance, the Fourier pseudospectral method is very fast through use of the fast Fourier transform (FFT), but requires domain truncation which is unnecessary for a rational basis. Radial basis functions are slow for a given number of grid points; however, they have a very flexible grid adaptation. To the best of our knowledge, there are no records regarding numerical solutions of the BO equation by using Sinc numerical methods.

In this paper, we propose a Sinc collocation method for solving the BO equation. Sinc numerical methods for solving ordinary and partial differential equations have increasingly become popular and have been extensively studied, in particular, for problems on unbounded domains and those having singularity at boundaries. The first Sinc method was introduced by Stenger [11] to solve two-point boundary value problems for second order differential equations. In the field of nonlinear partial differential equations, the use of Sinc numerical methods has shown tremendous potential. For instance, Al-Khaled [12] showed the utility of the Sinc Galerkin method for solving the Korteweg-de Vries equation. Recently, Mokhtari and Mohammadi [13] presented a meshfree method based on the Sinc collocation method to solve the generalized regularized long wave equation. Excellent overviews of the existing Sinc methods for solving ODEs, PDEs, and integral equations can be found in [14, 15].

The layout of this paper is as follows. We describe the formulation of the Sinc collocation method and the discretization of the Hilbert transform in Section 2. Section 3 is devoted to the Sinc collocation discretization of the BO equation. Furthermore, we examine the stability of the method by using a linearized stability analysis. Numerical results illustrating the merits of the new scheme are given in Section 4. Finally, we present our conclusions in Section 5.

2. Sinc Collocation Methods

In this section, we introduce some useful definitions and pertinent theorems of the Sinc function needed for space discretization of the BO equation. We use

to denote the set of all integers,

the set of all real numbers, and

the set of all complex numbers. Let u be a function defined on

and h the step-size. Then the Whittaker function is defined by the following series:

()

where S_j is given as follows:

()

and the Sinc function defined on the real line

is given by

()

Whenever the series given in (5) converges, u is approximated by using a finite number of terms. Therefore, for a positive integer N, (5) implies

()

The approximation of the nth derivative of the function u by the Sinc is given by

()

The Sinc collocation method requires derivatives of Sinc functions to be evaluated at collocation points. We can obtain explicit close form expressions for these; namely,

()

Lemma 1. The Hilbert transform of a function u can be approximated by

()

where

()

The entries of the Hilbert transform matrix at collocation point x_k = kh are given by

()

In order to state the convergence theorem of the Sinc collocation method, we introduce the following notation and definitions.

Definition 2. Let denote the infinite strip region with width 2d (d > 0) in the complex plane

()

For all 0 < ε < 1, let

be defined by

()

Let

be the Hardy space over the region

, that is, the set of functions such that

()

One then gets the following convergence results.

Theorem 3 (see [15].)Assume, with positive constants α, β, and d, that

(1) u belongs to ;

(2) u decays exponentially on the real line; that is,

()

Then we have

()

for some constants C₁ and C₂, where the mesh size h is taken as

()

The proof of the above Theorem 3 is beyond the scope of this paper. We refer the reader to [15] for a detailed discussion. Theorem 3 states that, if u is an analytic function on an infinite strip containing the real line and allows specific growth restrictions, then it has exponentially decaying absolute errors in the Sinc approximation. Similarly, the approximation of the derivatives and the Hilbert transform of u decay exponentially.

3. Construction of the Method

We consider the initial value problem for the Benjamin-Ono equation of the form

()

together with the following initial:

()

and the boundary conditions

()

Here

is a real valued function and

denotes the Hilbert transform defined by

()

where P denotes the Cauchy principal value.

In order to propose an unconditionally stable methodology, we discretize the time derivative of the BO equation using a classic finite difference formula by the θ-weighted (0 ≤ θ ≤ 1) scheme between two successive levels n and n + 1 as

()

where uⁿ = u(x, tⁿ), tⁿ = tⁿ⁻¹ + δt, and δt is the time step size.

The nonlinear term (uu_x) ⁿ⁺¹ in (24) can be approximated by Taylor expansion. We obtain the following formula:

()

Therefore

()

Equation (24) can be rewritten as

()

Now the space variable is discretized into collocation points

()

so that the solution of (20) is interpolated and approximated by means of the Sinc functions as

()

where the basis functions ξ_i(x) are given by

()

Here S_j(x) is defined as

()

and the two cubic interpolants [14]

()

are introduced to handle the radiation boundary conditions in (22).

The unknown parameters u_j in (29) are to be determined by collocation method. Therefore, for each collocation point x_i, (29) can be written as

()

The substitution of (33) into (27) at collocation points x_i yields the following equation:

()

To obtain the matrix representation of the expression (34), we introduce the following matrix and vector notations:

()

Thus we obtain the following system of N linear equations in N unknown parameters uⁿ⁺¹ which can be expressed in a matrix form

()

where

()

in which

()

where symbols “*” and “×” mean the component-wise and the matrix multiplications, respectively.

The stability of the approximation (36) is investigated by using the matrix method. The linearized version of (20) is obtained by assuming the quantity u in the nonlinear term uu_x as a local constant

. The error at timestep n is defined as

()

where

and

are the exact and the numerical solutions, respectively. The error matrix equation of the linearized BO equation is given by

()

where I = I⁽⁰⁾ and

. Now, let P = [I + θδtJ] ⁻¹[I + (1 − θ)δtJ]; then (40) becomes

()

The numerical scheme is stable if ∥P∥₂ ⩽ 1, or equivalently, ρ(P) ⩽ 1; that is, the spectral radius of the matrix P has to be smaller than or equal to one. From (40) it can be seen that the stability conditions are possible if all the eigenvalues of the matrix [I + θδtJ] ⁻¹[I + (1 − θ)δtJ] satisfy the following condition:

()

where λ_I and λ_J are the eigenvalues of the matrices I and J, respectively.

For θ = 0.5, the relation (42) becomes

()

If both λ_I and λ_J are complex eigenvalues, we write λ_I = a_h + ib_h and λ_J = a_k + ib_k. In this case, (43) can be rewritten as

()

The inequality (44) is satisfied if a_ha_k + b_hb_k⩾0. For real eigenvalues, the inequality (44) holds true for (λ_h⩾0 and λ_h⩾0) or (λ_h ⩽ 0 and λ_h ⩽ 0). This shows that scheme (36) is unconditionally stable if a_ha_k + b_hb_k⩾0 for complex eigenvalues and (λ_h⩾0 and λ_h⩾0) or (λ_h ⩽ 0 and λ_h ⩽ 0) for real eigenvalues.

For θ = 0, the inequality (42) becomes

()

In other words,

()

Therefore, when θ = 0, the scheme (42) is conditionally stable.

4. Numerical Results

The analytical soliton solutions of the BO equation are rational functions in x and t. For example, one and two soliton solutions are given, respectively, by (see [6, 16, 17])

()

where θ₁ = x − k₁t + ϕ₁, θ₂ = x − k₂t + ϕ₂, and k₁, k₂, ϕ₁, ϕ₂ are arbitrary constants. In this section, we examine the proposed algorithm using different test problems related to the propagation of one soliton and interaction of two soliton solutions. The accuracy of the scheme is measured by using the following error norms:

()

where u and

represent the exact and approximate solutions, respectively, and h is the minimum distance between any two points of set points for which the errors are evaluated. In our computational work, we use the collocation points

()

The BO equation possesses infinite conservation laws [5]; the first three are given as follows:

()

related to the mass, momentum, and energy. The quantities I₁, I₂, and I₃ are applied to measure the conservation properties of the collocation scheme calculated by

()

4.1. Propagation of Single Solitons

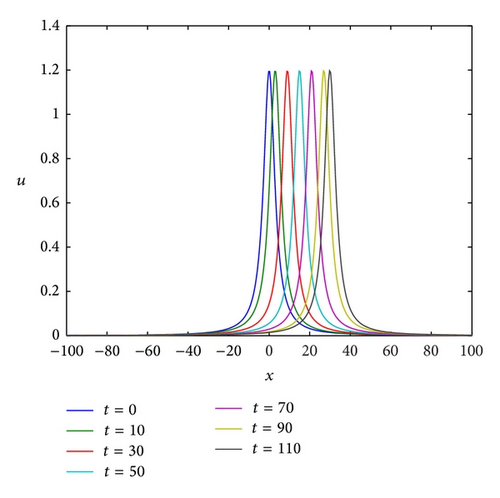
In this experiment, we consider the propagation of single solitons of the BO equation. The initial and boundary conditions are extracted from (47) and (22), respectively. The values of the parameters used in the numerical experiments are k₁ = 0.3, ϕ₁ = 0, θ = 1/2, the number of collocation points N = 200, and δt = 0.001. The soliton from which the initial condition is extracted (47) moves to the right across the space interval x ∈ [−100,100] when the time interval is t ∈ [0,110]. The numerical tests for this case are performed using the Sinc basis functions.

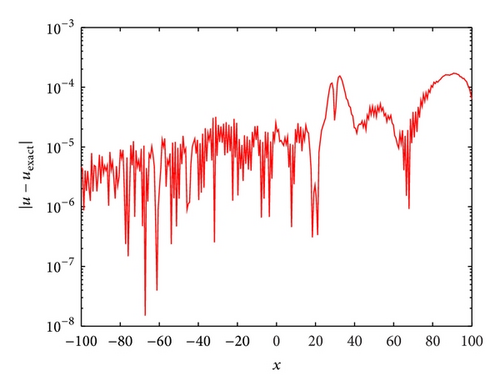
The error norms L_∞, L₂ and conservation quantities I₁, I₂, and I₃ are computed, which are shown in Table 1. From the numerical results given in Table 1 it is observed that, throughout the simulation, the error norms L_∞ remain less than 1.9803 × 10⁻⁴ and L₂ remains less than 9.3644 × 10⁻⁴, whereas the changes of the invariant I₁ are less than 10⁻⁴ and the invariants I₂ and I₃ at a given time t are equal to those of the initial value; our scheme is satisfactorily conservative. The numerical solutions at different time levels (a) and the absolute error (b) at time t = 110 are shown in Figure 1 for k₁ = 0.3, ϕ₁ = 0, θ = 1/2, the number of collocation points N = 200, and δt = 0.001 in the region x ∈ [−100,100].

Table 1. Invariants and errors for a single soliton of the BO equation. k₁ = 0.3, ϕ₁ = 0, N = 200, δt = 0.001, θ = 1/2, and x ∈ [−100,100].

Time	L_∞	L₂	I₁	I₂	I₃	CPU(s)
0	0	0	12.3007	7.5397	10.1788	0.000
10	3.3754E − 5	7.6966E − 5	12.3007	7.5397	10.1788	0.810
30	6.0085E − 5	1.8419E − 4	12.3008	7.5397	10.1788	2.098
50	8.5661E − 5	3.0307E − 4	12.3008	7.5397	10.1788	3.605
70	1.1471E − 4	4.5713E − 4	12.3008	7.5397	10.1788	5.505
90	1.5029E − 4	6.5433E − 4	12.3008	7.5397	10.1788	7.499
110	1.9803E − 4	9.3644E − 4	12.3008	7.5397	10.1788	9.931

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Propagation of soliton solutions (a) and absolute error (b) at t = 110 of the BO equation k₁ = 0.3, ϕ₁ = 0, N = 200, δt = 0.001, θ = 1/2, and x ∈ [−100,100].

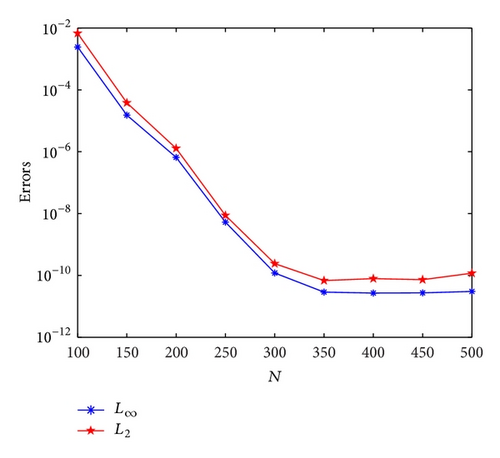
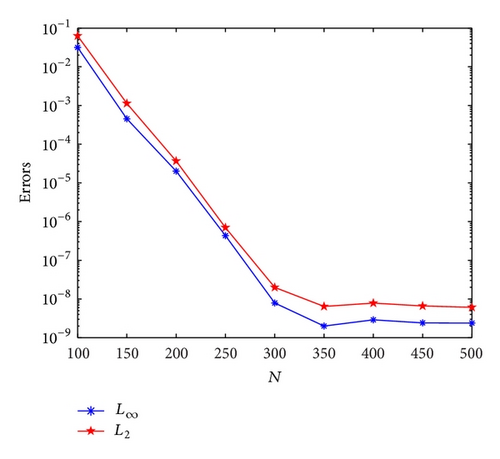
In the next experiment, we investigate the convergence of our approach in terms of the number of grid points N at time t = 1. To ensure that our scheme is not dominated by the time discretization, we choose δt = 10⁻⁵. We take the parameters such as k₁ = 0.4, k₂ = 0.1, ϕ₁ = 30, ϕ₂ = 0, δt = 10⁻⁵, θ = 1/2, and x ∈ [−100,100].

Figure 2 shows that the error norms L_∞ and L₂ converge exponentially for the propagation of one soliton solutions and for the interaction of two soliton solutions as we increase the number of grid points N.

4.2. Interaction of Two Solitons

Our second experiment pertains to the interaction of two soliton solutions of the BO equation having different amplitudes and travelling in the same direction. The initial and boundary conditions are extracted from (47) and (22).

To allow the interaction to occur, the experiment was run from t = 0 to 210 in the region [−100,100]. Figure 3 shows the interaction of two soliton solutions of BO equation for k₁ = 0.4, k₂ = 0.1, ϕ₁ = 30, ϕ₂ = 0, N = 200, δt = 0.001, θ = 1/2, and x ∈ [−100,100]. It can be seen that the faster pulse interacts with and emerges ahead of the lower pulse with the shape and velocity of each soliton retained. Because of the nature of the Sinc discretization, the Hilbert transform and matrix differentiation are explicitly obtained with exponential accuracy. The result in Figure 3 shows numerical interaction of the two soliton solution and its time evolution of the L₂ error from t = 0 to t = 210. In Figure 3(b), it is shown that the Sinc discretization maintains accurate results comparable to those given in [7, 10] for a long period. Therefore, a number of properties of the Benjamin-Ono equation can be checked numerically, including the exhibition of no phase shifts after interaction of the solitons.

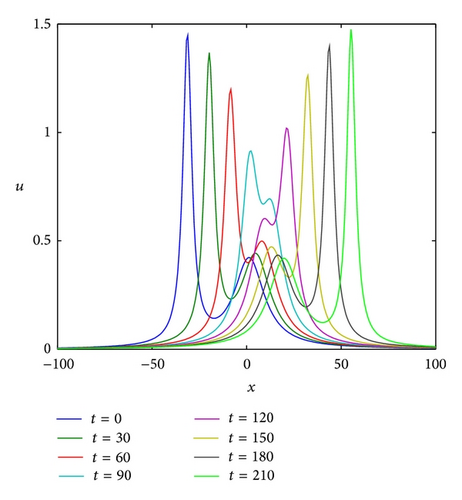
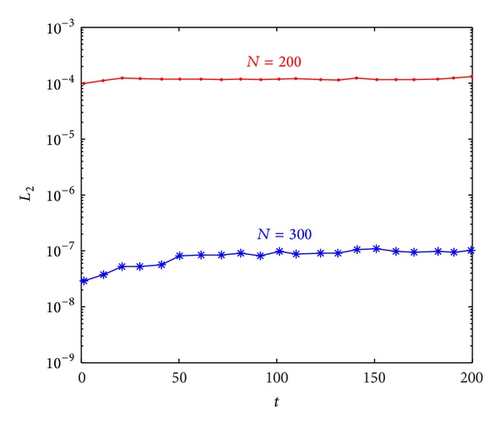
Numerical check on the conservation mass, momentum, and energy shows that the three quantities remain constant with respect to time as shown in Table 2. Propagation of the single solitary wave and two soliton integrations are simulated well with the proposed algorithms and conservation invariants do not change much during the computer run. Thus Sinc functions can be used to construct approximate numerical methods of the BO equation.

Table 2. Invariants and errors for interaction of two solitons of the BO equation. k₁ = 0.4, k₂ = 0.1, ϕ₁ = 30, ϕ₂ = 0, N = 200, δt = 0.001, θ = 1/2, and x ∈ [−100,100].

Time	L_∞	L₂	I₁	I₂	I₃	CPU(s)
0	0	0	24.0123	12.5716	16.7526	0.000
1	1.0200E − 4	1.4299E − 4	24.0124	12.5716	16.7526	0.278
30	2.7172E − 4	8.2385E − 4	24.0124	12.5716	16.7526	1.833
60	4.0996E − 4	1.4813E − 3	24.0124	12.5716	16.7526	3.854
90	5.6586E − 4	2.1770E − 3	24.0124	12.5716	16.7526	7.016
120	6.8573E − 4	2.9978E − 3	24.0124	12.5716	16.7526	8.961
150	8.5960E − 4	4.2343E − 3	24.0124	12.5716	16.7526	11.351
180	2.1269E − 3	6.6914E − 3	24.0124	12.5716	16.7526	14.142
210	3.1148E − 3	9.6304E − 3	24.0124	12.5716	16.7526	16.748

5. Conclusion

A numerical technique based on the Sinc collocation method has been presented for numerical solutions of the BO equation. The efficiency of the method is tested on the problems of propagation of a single soliton as well as interaction of two solitons. The accuracy of solutions is examined in terms of the L_∞, L₂ error norms, and the conservation quantities I₁, I₂, and I₃. Stability analysis is performed by the matrix method. The results obtained for the Sinc collocation are very close to analytical ones. Our algorithm was found to be unconditionally stable and exponentially convergent in space and a reliable numerical method for solving the BO equation. The method is easy to implement and compares favourably to Fourier-based spectral methods without any assumptions on periodicity.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgment

Edson Pindza is thankful to Brad Welch for the financial support from RidgeCape Capital.

References

1 Weideman J. A. C., Computing the Hilbert transform on the real line, Mathematics of Computation. (1995) 64, no. 210, 745–762, https://doi.org/10.2307/2153449, MR1277773, ZBL0830.65127.
Google Scholar
2 Benjamin T. B., Internal waves of permanent form in fluids of great depth, Journal of Fluid Mechanics. (1967) 29, no. 3, 559–592, https://doi.org/10.1017/S002211206700103X.
Google Scholar
3 Ono H., Algebraic solitary waves in stratified fluids, Journal of the Physical Society of Japan. (1975) 39, no. 4, 1082–1091, MR0398275, 2-s2.0-33646882954.
Google Scholar
4 Kenig C. E., Ponce G., and Vega L., Well-posedness and scattering results for the generalized Korteweg-de Vries equation via the contraction principle, Communications on Pure and Applied Mathematics. (1993) 46, no. 4, 527–620, https://doi.org/10.1002/cpa.3160460405, MR1211741, ZBL0808.35128.
Google Scholar
5 Abdelouhab L., Bona J. L., Felland M., and Saut J., Nonlocal models for nonlinear, dispersive waves, Physica D. (1989) 40, no. 3, 360–392, https://doi.org/10.1016/0167-2789(89)90050-X, MR1044731, 2-s2.0-0024901384.
10.1016/0167-2789(89)90050-X
Google Scholar
6 Satsuma J. and Ishimori Y., Periodic wave and rational soliton solutions of the Benjamin-Ono equation, Journal of the Physical Society of Japan. (1979) 46, no. 2, 681–687, https://doi.org/10.1143/JPSJ.46.681, 2-s2.0-0006533697.
Google Scholar
7 James R. L. and Weideman J. A. C., Pseudospectral methods for the Bejamin-Ono equation, Advances in Computer Methods for Partial Differential Equations VII, 1992, 371–377.
Google Scholar
8 Miloh T., Prestin M., Shtilman L., and Tulin M. P., A note on the numerical and N-soliton solutions of the Benjamin-Ono evolution equation, Wave Motion. (1993) 17, no. 1, 1–10, https://doi.org/10.1016/0165-2125(93)90085-T, MR1203089, 2-s2.0-0040782431.
Google Scholar
9 Thomée V. and Vasudeva Murthy A. S., A numerical method for the Benjamin-Ono equation, BIT Numerical Mathematics. (1998) 38, no. 3, 597–611, https://doi.org/10.1007/BF02510262, MR1652789, 2-s2.0-0039596680.
Google Scholar
10 Boyd J. P. and Xu Z., Comparison of three spectral methods for the Benjamin-Ono equation: Fourier pseudospectral, rational Christov functions and Gaussian radial basis functions, Wave Motion. (2011) 48, no. 8, 702–706, https://doi.org/10.1016/j.wavemoti.2011.02.004, MR2853734, 2-s2.0-80755189048.
Google Scholar
11 Stenger F., A Sinc-Galerkin methods for solution of boundary value problems, Mathematics of Computation. (1979) 33, 85–109.
Google Scholar
12 Al-Khaled K., Sinc numerical solution for solitons and solitary waves, Journal of Computational and Applied Mathematics. (2001) 130, no. 1-2, 283–292, https://doi.org/10.1016/S0377-0427(99)00376-3, MR1827987, ZBL1010.65043, 2-s2.0-0035338865.
Google Scholar
13 Mokhtari R. and Mohammadi M., Numerical solution of GRLW equation using Sinc-collocation method, Computer Physics Communications. (2010) 181, no. 7, 1266–1274, https://doi.org/10.1016/j.cpc.2010.03.015, MR2644968, 2-s2.0-77953131119.
Google Scholar
14 Lund J. and Bowers K. L., Sinc Methods For Quadrature and Differential Equations, 1992, SIAM, Philadelphia, Pa, USA, https://doi.org/10.1137/1.9781611971637, MR1171217.
Google Scholar
15 Stenger F., Numerical Methods Based on Sinc and Analytic Functions, 1993, Springer, New York, NY, USA.
Google Scholar
16 Matsuno Y., Exact multi-soliton solution of the Benjamin-Ono equation, Journal of Physics A: Mathematical and General. (1979) 12, no. 4, 619–621, https://doi.org/10.1088/0305-4470/12/4/019, 2-s2.0-0037786131.
Google Scholar
17 Matsuno Y., Interaction of the Benjamin-Ono solitons, Journal of Physics A: Mathematical and General. (1980) 13, no. 5, 1519–1536, https://doi.org/10.1088/0305-4470/13/5/012, MR573163, 2-s2.0-0038800762.
Google Scholar

Citing Literature

All articles

Sinc Collocation Method for Solving the Benjamin-Ono Equation

Abstract

1. Introduction

2. Sinc Collocation Methods

3. Construction of the Method

4. Numerical Results

4.1. Propagation of Single Solitons

4.2. Interaction of Two Solitons

5. Conclusion

Conflict of Interests

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Sinc Collocation Method for Solving the Benjamin-Ono Equation

Abstract

1. Introduction

2. Sinc Collocation Methods

3. Construction of the Method

4. Numerical Results

4.1. Propagation of Single Solitons

4.2. Interaction of Two Solitons

5. Conclusion

Conflict of Interests

Acknowledgment

References

Citing Literature

Figures

References

Related

Information