Volume 2014, Issue 1 362787

Research Article

Open Access

Movement Control in Recovering UUV Based on Two-Stage Discrete T-S Fuzzy Model

Zheping Yan,

Zheping Yan

College of Automation, Harbin Engineering University, Harbin, Heilongjiang 150001, China hrbeu.edu.cn

Search for more papers by this author

Bing Hao,

Corresponding Author

Bing Hao

[email protected]

College of Automation, Harbin Engineering University, Harbin, Heilongjiang 150001, China hrbeu.edu.cn

College of Computer and Control Engineering, Qiqihar University, Qiqihar, Heilongjiang 161006, China qqhru.edu.cn

Search for more papers by this author

Yibo Liu,

Yibo Liu

College of Automation, Harbin Engineering University, Harbin, Heilongjiang 150001, China hrbeu.edu.cn

Search for more papers by this author

Shuping Hou,

Shuping Hou

College of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin, Heilongjiang 150001, China hrbeu.edu.cn

Search for more papers by this author

Zheping Yan,

Zheping Yan

College of Automation, Harbin Engineering University, Harbin, Heilongjiang 150001, China hrbeu.edu.cn

Search for more papers by this author

Bing Hao,

Corresponding Author

Bing Hao

[email protected]

College of Automation, Harbin Engineering University, Harbin, Heilongjiang 150001, China hrbeu.edu.cn

College of Computer and Control Engineering, Qiqihar University, Qiqihar, Heilongjiang 161006, China qqhru.edu.cn

Search for more papers by this author

Yibo Liu,

Yibo Liu

College of Automation, Harbin Engineering University, Harbin, Heilongjiang 150001, China hrbeu.edu.cn

Search for more papers by this author

Shuping Hou,

Shuping Hou

College of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin, Heilongjiang 150001, China hrbeu.edu.cn

Search for more papers by this author

First published: 04 November 2014

https://doi.org/10.1155/2014/362787

Citations: 1

Academic Editor: Xiaojie Su

Share a link

Email
Wechat
Bluesky

Abstract

A two-stage discrete T-S fuzzy model controller, which is formed by a motion controller and a dynamic controller connected in series, is presented to solve UUV (unmanned underwater vehicle) movement control problem for recovering. The motion controller is designed based on the uncertain T-S model and the concept of discrete fuzzy vector. The position error between UUV and moving platform as the input of the motion controller is converted into the speed commands of UUV at the next time. The dynamic controller design is based on the theory of fuzzy region model and a relaxed condition for Lyapunov stabilization function is derived in the form of linear matrix inequalities, which generate force and torque required to complete the recovery task. The feasibility and the efficiency of the proposed control scheme are illustrated through the simulations that UUV follows moving platform.

1. Introduction

Since invented, UUV plays an important role in many missions, such as the exploration and military applications. There is an energy storage limitation for underwater vehicle to perform the sustained missions. After navigating for a period of time, a UUV has to return to the moving platform to replay data, download new missions, and so forth, so the recovery operation of UUV is an indispensable process. Due to its importance as technical support for autonomic recovery of UUV, the research of the motion and dynamic control method is of significant value in the process of recovery.

With the development of a control engineering theory, many techniques have been applied to the control of UUV. Due to its inherent nonlinearity in the dynamic model, nonlinear techniques, like neural network control [1], adaptive control [2, 3], fuzzy control [4, 5], sliding mode control [6, 7], and back stepping control based on Lyapunov stability theory [8], have been widely applied.

The main advantage of T-S fuzzy system is that its outputs can be expressed as a function of its inputs [9]. With this modeling method the nonlinear system is described as a dynamic linear combination of several linear subsystems by IF-THEN rules. For each T-S linear subsystem, individual controller can be designed to satisfy certain performance. Then the global controller is built using PDC (parallel distribute compensation) framework. Because of the ability to approximate any smooth nonlinear function at any accuracy, T-S fuzzy model with time delay is widely studied in theory and applications [10]. The problem of H_∞ control of T-S fuzzy systems is considered in [11]. A more concise condition of system stability and controller existence is proposed. The concept of T-S fuzzy region is presented in [12]. The T-S fuzzy region model is obtained by means of the uncertain T-S fuzzy model and the fuzzy region controller is developed by means of the method of PDC.

Robust UUV tracks and arrives to the recovering platform with the presence of environmental disturbance, which is one of the most difficult and challenging problems in realizing recovery in high accuracy. Fuzzy logic control approach, which offers high robustness and resistance to disturbance, has been adopted recently in many papers to deal with nonlinear UUV control problem, such as [13, 14]. Some problems of UUV control have been solved successfully using fuzzy methods. A fuzzy algorithm appears to be the most suitable solution for the problem of recovery. In the study of other similar problems, tracking planners have been designed to compute the entire trajectory for the UUV [15, 16]. This requires very accurate and timely information about the dynamics of UUV and its environment disturbance, which, however, cannot be obtained easily and accurately. In order to overcome these lacks, two-stage T-S fuzzy schedule is designed in this paper. In the designed control system, the motion controller and the dynamic controller are connected in series to form a two-stage controller. The concept of discrete fuzzy vector and the theory of fuzzy region model are adopted in control algorithm which does not rely on each specific waypoint or each accurate target points although the platform is moving all the time. With the same equipment, the required accuracy can be obtained when the vehicle is approaching the docking device in recovering process.

2. Problem Statement

In general, the process that a moving platform autonomously recovers a UUV can be divided into three typical stages: rendezvous stage, homing stage, and docking stage. This paper aims at the second stage, in which UUV tracks the moving platform, arrives the area near the docking mechanism, and then waits for the next docking stage.

The designed motion planning system consists of fuzzy motion controller and dynamics controller, which provides the necessary speed and course guidance to a UUV in the condition that the platform is moving all the time. Some assumptions in planning approach are as follows.

(1)
In this stage, moving platform keeps cruising at a low speed along a certain track near the rendezvous and is ready for docking.
(2)
After reaching the set point, UUV conducts real-time tracking of the moving platform immediately.
(3)
The transmitter unit of ultrashort baseline (USBL) sonar is mounted on the docking mechanism of moving platform, and the receiving unit of USBL is mounted on UUV. And UUV can detect the position of docking device of moving platform timely using USBL.
(4)
When the distance between UUV and docking mechanism on the moving platform is less than 10 m, UUV is considered to keep up with the moving platform. At the moment when the docking instruction is received from the moving platform, the working state of UUV shifts into the docking phases.

3. Design Scheme

Since UUV is an underactuated device with a lateral drift angle, if only considering the kinematic design problem and regardless of the second-order nonholonomic dynamics problem, the system control performance cannot be guaranteed. The proposed fuzzy recovering scenario in this work includes two parts which are connected in the series, described in Figure 1. The former part is UUV motion planning controller, which is designed by the idea of the uncertain T-S Fuzzy model. The inputs of motion planning controller are position information of UUV relative to the moving platform and the outputs are the speed commands of UUV at the next time. Uncertain T-S fuzzy model is ascertained by fuzzy vector, and its consequent parameters are identified by the recursive least squares algorithm. The latter part is UUV dynamical controller to generate force and torque required to complete the recovery task, in which the idea of the fuzzy region model is adopted. Both of the parts apply the advanced fuzzy algorithm and solve the problem presented in this paper perfectly by the union of them.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Two-stage discrete T-S fuzzy control system.

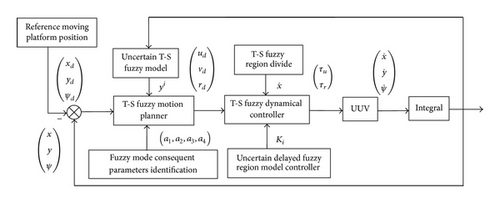
4. Motion Planning Controller Design

This section presents the research approach and the motion planning scheme in recovering process.

4.1. Motion Planning Strategy

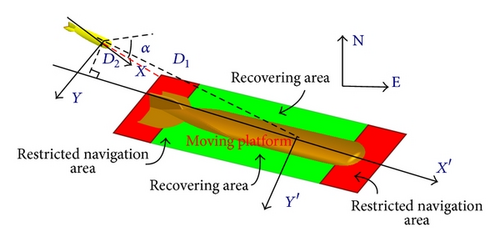
A motion planning strategy in recovering process is conceptualized on how UUV should follow and approach the moving platform in the same heading with minimum distance error under disturbed situation. While tracking the moving platform, UUV must avoid the certain areas in order to ensure the UUV safety, to avoid the collision of UUV and moving platform and to ensure the recovery success rate. The area is called restricted navigation area.

To determine the best motion planning approach for the UUV following moving platform, four competition goals are identified [17].

(1)
UUV has to avoid the restricted navigation area during the whole process (including its approaching moving platform) while keeping tracking of moving platform. In this way, the moving platform should not simply be treated as a particle and the restricted navigation area must be modeled according to the shape of the ship. Docking mechanism is located in the front of moving platform hull. In this paper the two restricted navigation areas of UUV are set up around the moving platform, as shown in Figure 2.
(2)
To maintain small distance to moving platform, D₁ and D₂ are defined as the vertical and horizontal distances between UUV and moving platform center in the xy-plane) and α is defined as the angle between UUV forward direction and moving platform forward direction.
(3)
Without any lateral thrusters, it is very difficult to maintain UUV heading toward moving platform perfectly in case of the water current perturbing. The fuzzy algorithm in this paper is recursive and it can work out these problems, for the targets are constantly redefined and the recovering of the vehicle is ensured as it is moving toward moving platform.

4.2. Discrete Fuzzy Vector Map

The novel idea adopted in this work [9, 18–21] is to implement a fuzzy controller by discretizing the following regions into cells. In the regions, a fuzzy vector field for recovering is generated. Figure 3 illustrates the discrete vector. The fuzzy vector map in the local frame is represented by D₁, D₂, and α axes. The distances D₁and D₂ and the angle α are not drawn in scale. The fuzzy vector field shown in local map is being discretized into 9 cells (c1–c9), explained in Section 4.3, which can be used for motion guidance.

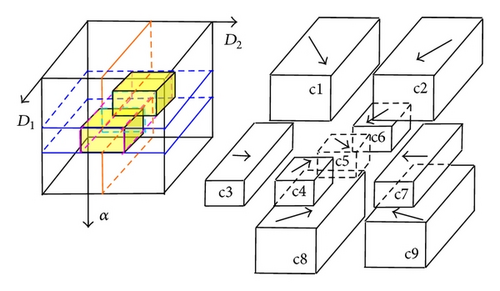
Depending on D₁, D₂, and α, the respective cells and algorithms will be used to determine the desired vehicle speed and heading for motion at the next time. The heading and speed commands from the motion planning controller are subsequently sent to the T-S fuzzy dynamics controllers to control thrusters and rudders.

4.3. The Uncertain T-S Fuzzy Model

In order to successfully achieve the vehicle following moving platform, the T-S fuzzy model is constructed. The main advantage of this fuzzy system is that its outputs can be expressed as a function of its inputs [9]. With this modeling method the nonlinear system is described as a dynamic linear combination of several linear subsystems by IF-THEN rules. For each T-S linear subsystem, individual controller can be designed to satisfy certain performance. Then the global controller is built using PDC (parallel distribute compensation) framework. In this motion planning controller based on T-S fuzzy, there are three inputs (D₁, D₂ and α) and three outputs (longitudinal speed, lateral speed, and heading).

The function of this system can be generally represented as

()

where yⁱ represents either the speed output or heading output for the ith rule, x₁, x₂, and x₃ are the first, second, and third inputs, respectively, and

, and

are the parameters expressed for the ith rule.

In this paper, the defuzzification method is weighted average method, which is extensively used in engineering. Consider

()

where u_d, v_d, and r_d are the final crisp values or defuzzified output, which represent vehicle speed and heading. u_i, v_i, and r_i are the fuzzy function output expressed in local fuzzy frame map in the ith rule. ω_i and η_i are the defined parameters for the ith rule. M_ij is the membership function for the jth input x_j in the ith rule [20, 21].

The set of linguistics values for the first input x₁ is {very far, far, near, over}, the set of linguistics values for the second input x₂ is {left, small left, center, small right, right}, and for the set of third input x₃ is {very big, big, middle, small}. The membership functions for linguistics variables are shown in Figure 4.

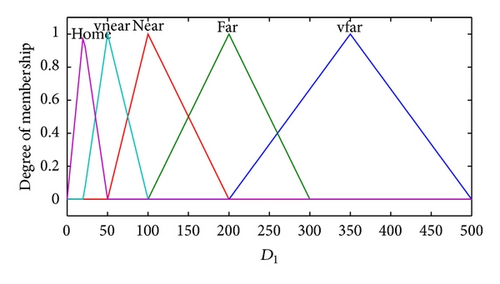
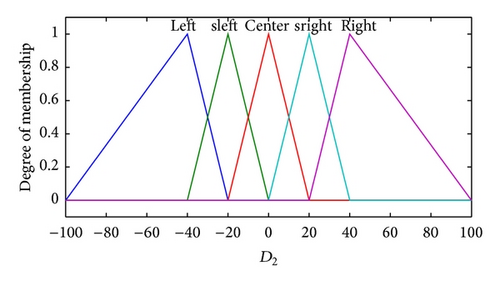
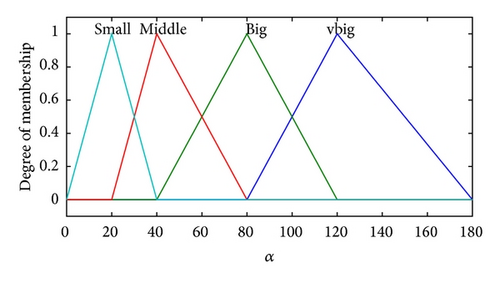
The choices of all coefficients in function (1) would impact the following performance. To gain smooth surface of the speed and heading of control output and not to exhibit discontinuities between adjacent sectors, all the coefficients in fuzzy model could be obtained by identification. The process of identifying the coefficients would be stated in detail in the next section.

4.4. Fuzzy Parameters Identification

In the foregoing model building, a model structure process has just been built and the parameters of model have not been given. Then Fuzzy model consequent parameters are given to be some specific values by identification method. Due to its simplicity and high identification accuracy, the recursive least squares method is adopted in this paper to identify the model parameters.

T-S fuzzy system structure model is as follows:

()

where k represents the kth sampling in the above formulas.

System output can be expressed as

()

where

()

Here A_ik is membership function, taken as the normal type, whose analytical formula is as follows:

()

For the T-S model defined by formula (1), the input variables and parameters are

()

The output variables of T-S model are defined as

()

Here the parameter vector A is the consequent parameter to be identified.

In order to obtain optimization parameter vector A online by iterative mode and avoid solving the inverse matrix, the model consequent parameters achieve online learning by recursive least squares method.

The objective function is defined as

()

where

is the actual value of the system output and y_i is the output of the model. The minimum value of the objective function J may be determined by a standard least squares method or Kalman filtering method. Consider

()

Let X_k be the kth row vector of X and let Y_k be the kth component of Y, then recursive algorithm is as follows:

()

Set the initial parameters A₀ = 0 and S₀ = κI, where κ is the real number generally more than 10000, I is a M × M dimensional unit matrix, and M = (m + n + 1) × N.

5. Dynamic Controller Design

For UUV underwater with recovery mission, motion planning controller module has been completed in the previous section and the expectation of UUV position and velocity information are acquired. This information will be used as the inputs of the next stage of dynamic controller. This section uses parameter uncertain T-S fuzzy region model to design UUV tracking moving platform controller.

5.1. The Concept of T-S Fuzzy Region

The literature [12] puts forward the concept of fuzzy regions. Namely, in practice, the premise vector Z(t) ∈ Rⁿ of the structure of the fuzzy system has at most 2ⁿ rules to be activated at any moment. Therefore, at any time only 2ⁿ LMIs need to be solved in designing the fuzzy controller. Obviously it would be much easier to solve such control problems with this model.

Let r, G, and f be the number of system rules, the number of fuzzy regions, and the number of activated rules in each fuzzy region, respectively. g is the number of premise variables and q is the number of fuzzy sets of every variable. For general T-S fuzzy models, (12) can be obtained:

()

5.2. Uncertain Time-Delay T-S Fuzzy Region Model

This paper is to transform the uncertain T-S model region in document [12] into the T-S uncertain time-delay fuzzy region model. The system model is expressed as follows:

()

RRⁱ is the ith rule of the T-S fuzzy region model. Region_in is the ith fuzzy region of z_n(t), which essentially is a special fuzzy set and its membership function structure is shown in Figure 5.

, and

denote one fuzzy set, respectively, q denotes the total number of membership functions in z_n(t), q = 1, …, 4. (A_li, B_li) represents the ith fuzzy subsystem of the lth fuzzy region, 1 ≤ l ≤ f. These subsystem numbers are arranged from small to large according to the original fuzzy system serial number.

, and

are the uncertain coefficient matrices and delay coefficient matrices of the system, respectively, the subscript determining rule of which is the same as A_li, B_li.

and α_l = α_l(z(t)) is the normalized activation degree of the fuzzy rules of the corresponding fuzzy region, similar to the normalized activation degree η_i(z(t)) of the general T-S fuzzy model. Here, T-S fuzzy region model is equivalent to the two level of T-S fuzzy model structure based on the original T-S fuzzy model membership structure information, and whose consequent part is equivalent to a local T-S fuzzy model. t_d is the delay time. The state equation (14) of uncertain time-delay T-S fuzzy region mode can be determined. Consider

()

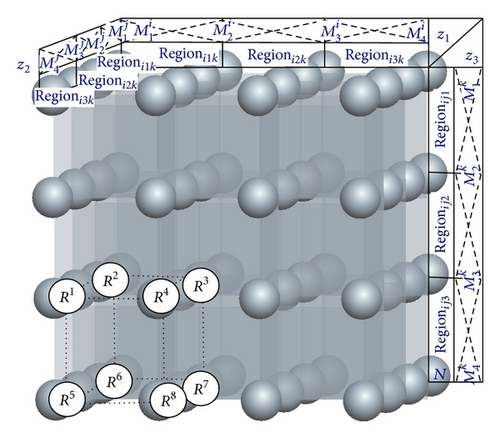
Region_ij(z_j(t)) represents the membership of z_j(t) in the fuzzy region Region_ij.

Assumption. The matrix

of parameter uncertainty is norm bounded, in the form of

()

where D_li,

, and

are known real constant matrices of appropriate dimensions and F_li(t) is an unknown matrix function with Lebesgue-measurable elements and satisfies F_li(t) ^TF_li(t) ≤ I, I is a unit matrix.

5.3. Robust Fuzzy Region Controller Design

In order to prove the main theorem in this section, the following lemmas are written:

Lemma 1. If a piecewise smooth quadratic Lyapunov equation (17) satisfies condition (18),

()

where,

, P_i ∈ R^n×n, and i = 1,2, …, L, then the autonomous system (14) is globally asymptotically stable at equilibrium point x = 0.

Lemma 2. Given constant matrices D, E, and a symmetric constant matrix H of appropriate dimensions, the following inequality holds:

()

if only for some ε > 0,

()

where F satisfies F^TF ≤ R,

The PDC fuzzy controller is

()

is the feedback gain of the controller.

By putting (21) into (14),

()

when i ≠ j,

[12], formula (22) is simplified as

()

For the T-S fuzzy model of uncertain nonlinear systems, based on the concept of fuzzy region, the following stability theorem is obtained:

Theorem 3. If there are symmetric and positive definite matrices P_i, Q_i, some matrices , positive scalars ε_li, and the following LMIs are satisfied:

()

where i = 1,2, …L; l = 1,2, …, f, and

, then the fuzzy controller (21) makes the T-S fuzzy region system (14) globally asymptotically stable.

Proof. (1) The Lyapuov function of each fuzzy region is defined as

()

(2)
According to the theory of Lyapuov, solve
- (i)
  According to the Newton-Leibniz formula, the time derivative of V_i(x) is
  ()
- (ii)
  Based on (22), (26) can be rewritten as follows:
  ()
- In order to express simply, define the following variables:
  ()
- (iii)
  Applying Assumption into (28), then
  ()
  
  ()
- (iv)
  Substitute (29) and (30) into (27), and let , then
  ()
(3)
According to Lemmas 1 and 2 and applying Schur complement theorem, the quadratic matrix inequality will be line Matrix inequality. Then the conclusion in Theorem 3 is obtained.

6. Movement Controller of following Moving Platform Design

6.1. Fuzzy Region Control Law Design

Without water current influence, heave direction movement and the rotation in the roll and pitch direction are ignored, then the kinetic equation of UUV can be simplified as the compressed form as the following [12]:

()

where η = [x, y, ψ] ^T, v = [u, v, r] ^T, τ = [τ_u, 0, τ_r], u = Vcos⁡β, v = Vsinβ, M = diag⁡{m_u, m_v, m_r}, and D = diag⁡{d_u, d_v, d_r},

()

u, v, and r are vertical velocity, lateral velocity, and rotary angular velocity of the UUV, respectively, and V is synthetic speed of robot and β is lateral drift angle.

In order to design a T-S fuzzy region control law, first of all, formula (32) is expressed as T-S fuzzy model. u, v, and r are selected as antecedent variables and their membership functions are triangular. Each antecedent variable in their own domain has three Fuzzy sets.

6.2. Simulation Analysis

Take an underactuated underwater vehicle SIRENE as an example, the actual parameters of the robot model from towing experiment in the literature [22] is given as the following:

()

Put these structure parameters into UUV model to get the coefficient matrices of UUV fuzzy subsystems model, respectively. Consider

()

ξ_i, φ_i, θ_i, ρ_i, ϕ_i, and ζ_i represent the fuzzy system uncertain parameters and change within 30% of the nominal value.

According to PDC design concept, the fuzzy controller is composed of eight control rules. After the conditions of Lemma 1 being solved with MATLAB’s LMI control toolbox, the following coefficient matrices are gotten:

()

In simulation experiment, the trajectory of moving platform is a circle with the radius R of 300. The initial position and attitude of moving platform are x_d = R, y_d = 0, and ψ_d = π/2. Moving platform speed is 2 m/s. The initial position and attitude of UUV are x₀ = R − R/3, y₀ = −30, and ψ₀ = π/6. The minimum speed of UUV is set to be 1 kn and the maximum speed is set to be 4 kn. The maximum deflection angle velocity is 10 deg/s. The maximum thrust of the propeller output is 2000 N and the output rudder angle range of vertical rudder is [−30,30] deg. Sampling time in simulation is 1 s.

In order to be compared with the algorithm proposed in this paper, another two-stage Mamdani fuzzy controller is designed in simulation. The inputs and outputs of this traditional fuzzy controller are the same as the proposed controller. The number of fuzzy sets and the number of fuzzy rules are set by experience. The following simulations are designed to demonstrate the performance of the two control scheme in the movement control of the UUV in recovering process.

Figures 6 and 7 show the longitudinal position and lateral position error curve of UUV using the two controllers. All the position errors are close to zero in the simulations. However the position errors of Mamdani fuzzy controller are more obvious. The simulations show the UUV can keep up with the moving platform quickly by the proposed controller, which meets the requirements of the UUV recovery process.

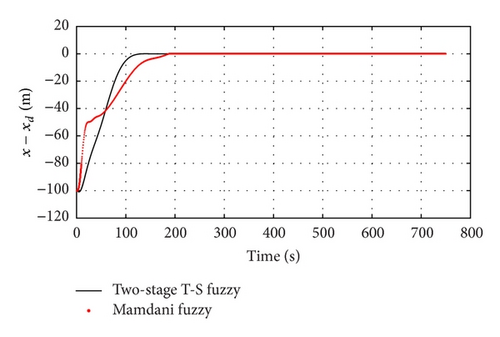
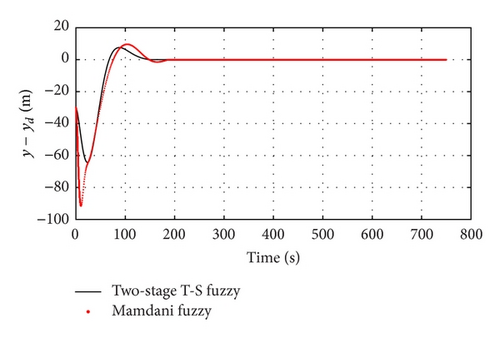
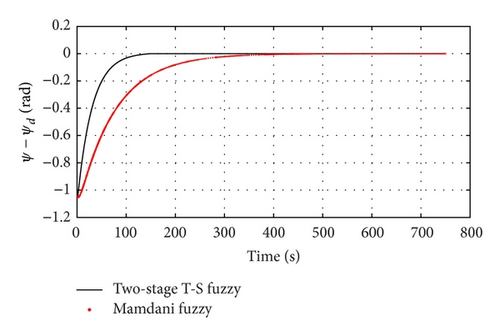
Figure 8 shows the UUV heading error curve with the two control algorithms. By comparing the two curves, it can be seen that the pitch angle of UUV keeps up with the moving platform pitch angle (the pitch angle of reference trajectory) more quickly. The error around the corner is about three degrees within normal error range.

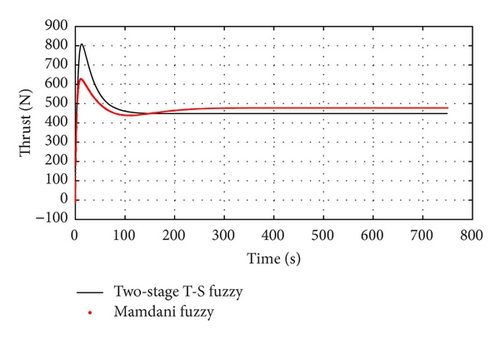
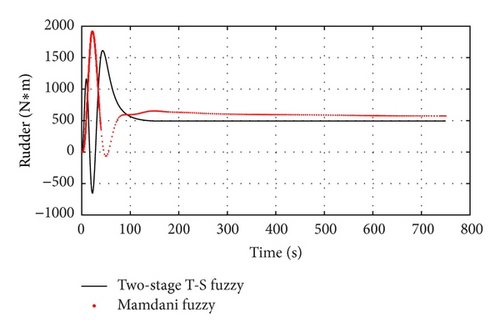
The response curves of the thrust and the rudder are shown in Figures 9 and 10. The two simulations show that there are little differences in the response curve of force and torque generated by the two controllers. By using them, UUV can track moving platform as soon as possible, but in the starting stage of the tracking task, the propeller of and the vertical rudder of the new controller had the larger outputs and the rudder did not reach saturation state. No violent oscillation occurred to the propeller and rudder during the process of tracking.

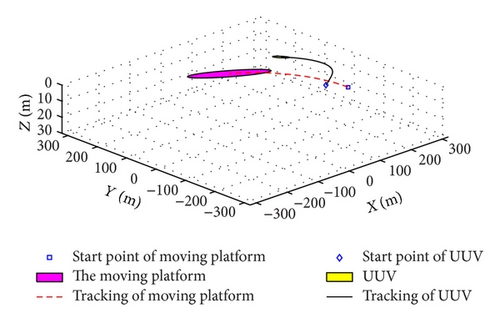
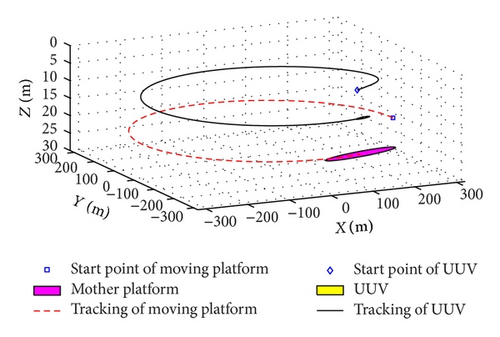
Figures 11 and 12 show the UUV and moving platform trajectory in the recovering process. Figure 11 is the stage when UUV did not keep up with moving platform. UUV has detected the restricted navigation zones on the stern of moving platform and began to evade it while maintaining tracking the moving platform. Figure 12 is the final stage of the simulation indicating that UUV keeps following the moving platform in the whole process after tracking on it, which meets the requirements of the UUV recovery process.

7. Conclusions

This paper proposed a new movement control approach to the problem of recovering UUV. The controller takes the position information as a planning element, real-time plan speed, and heading to guide UUV to keep tracking moving platform. This approach does not require any real-time velocity, thereby greatly reduces the cost of the docking platform. The proposed two-stage T-S fuzzy theory is based on the concept of discretization to generate the fuzzy map and the uncertain fuzzy region model, which can reduce LMIs and loosen the stable conditions. The simulation results demonstrate the feasibility and the effectiveness of the recovering guidance approach.

UUV underwater recovering is a difficult research field. UUV movement is affected by the ocean currents in marine environment; thus, the tracking of the UUV planning, tracking control, and the movement of moving platform under the action of ocean currents should be taken into consideration in the further research.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

This work is partially supported by the National Natural Science Foundation of China under Grant 51179038 and 51109043 and the Program for New Century Excellent Talents in University under Grant NCET-10-0053.

References

1 Giampiero C., Manu S., Anthony C. J., and Mario I., Neural network augmentation of linear controller with application to underwater vehicles, Proceeding of the American Control Conference, September 2000, Chicago, Ill, USA, IEEE, 75–79, https://doi.org/10.1109/ACC.2000.878775.
10.1109/ACC.2000.878775
Google Scholar
2 Barambones O. and Etxebarria V., Robust adaptive control for robot manipulators with unmodelled dynamics, Cybernetics and Systems. (2000) 31, no. 1, 67–86, https://doi.org/10.1080/019697200124928, ZBL1017.93071, 2-s2.0-0033993182.
10.1080/019697200124928
Web of Science® Google Scholar
3 Santhakumar M. and Kim J., Modelling simulation and model reference adaptive control of autonomous underwater vehicle-manipulator systems, Proceedings of the 11th International Conference on Control Automation and Systems, 2011, Daejeon, South korea, Ocean Robotics and Intelligent Laboratory, Division of Ocean systems and Engineering.
Google Scholar
4 Mbede J. B., Wei W., and Zhang Q., Fuzzy and recurrent neural network motion control among dynamic obstacles for robot manipulators, Journal of Intelligent and Robotic Systems. (2001) 30, no. 2, 155–177, https://doi.org/10.1023/A:1008194912825, 2-s2.0-0034825629.
10.1023/A:1008194912825
Web of Science® Google Scholar
5 Chiang H.-H., Chen Y.-L., and Lee T.-T., Multi-stage with neuro-fuzzy approach for efficient on-road speed sign detection and recognition, International Journal of Innovative Computing, Information and Control. (2013) 9, no. 7, 2919–2939, 2-s2.0-84880080059.
Google Scholar
6 Lee P.-M., Hong S.-W., Lim Y.-K., Lee C.-M., Jeon B.-H., and Park J.-W., Discrete-time quasi-sliding mode control of an autonomous underwater vehicle, IEEE Journal of Oceanic Engineering. (1999) 24, no. 3, 388–395, https://doi.org/10.1109/48.775300, 2-s2.0-0032634016.
10.1109/48.775300
Web of Science® Google Scholar
7 Soltanpour M. R., Zolfaghari B., Soltani M., and Khooban M. H., Fuzzy sliding mode control design for a class of nonlinear systems with structured and unstructured uncertainties, International Journal of Innovative Computing, Information and Control. (2013) 9, no. 7, 2713–2726, 2-s2.0-84880071326.
Google Scholar
8 Santhakumar M. and Asokan T., Coupled, non-linear control system design for autonomous underwater vehicle (AUV), Proceedings of the 10th International Conference on Control, Automation, Robotics and Vision (ICARCV ′08), December 2008, Hanoi, Vietnam, 2309–2313, https://doi.org/10.1109/ICARCV.2008.4795893, 2-s2.0-64649099344.
10.1109/ICARCV.2008.4795893
Google Scholar
9 Smith S. M., Rae G. J. S., and Anderson D. T., Application of fuzzy logic to the control of an autonomous underwater vehicle, 2, Proceedings of the 2nd IEEE International Conference on Fuzzy Systems, 1993, San Francisco, Calif, USA, 1099–1106, https://doi.org/10.1109/FUZZY.1993.327361.
10.1109/FUZZY.1993.327361
Google Scholar
10 Su X., Shi P., Wu L., and Basin M. V., Reliable filtering with strict dissipativity for T-S fuzzy time-delay systems, IEEE Transactions on Cybernetics. (2014) PP, no. 99, https://doi.org/10.1109/TCYB.2014.2308983.
10.1109/TCYB.2014.2308983
Google Scholar
11 Su X., Wu L., Shi P., and Song Y.-D., H_∞ model reduction of Takagi-Sugeno fuzzy stochastic systems, IEEE Transactions on Systems, Man, and Cybernetics B: Cybernetics. (2012) 42, no. 6, 1574–1585, https://doi.org/10.1109/TSMCB.2012.2195723, 2-s2.0-84869491170.
10.1109/TSMCB.2012.2195723
PubMed Web of Science® Google Scholar
12 Sun C., Chung Y. H., and Chang W. J., Design of takagi-sugeno fuzzy-region controller based on fuzzy-region concept, rule reduction and robust control technique, 2, Proceedings of the IEEE International Conference on Networking, Sensing and Control, 2004, IEEE, 914–919, https://doi.org/10.1109/ICNSC.2004.1297069.
10.1109/ICNSC.2004.1297069
Google Scholar
13 Amjad M., Ishaque K., Abdullah S. S., and Salam Z., An alternative approach to design a Fuzzy Logic Controller for an autonomous underwater vehicle, Proceedings of the IEEE International Conference on Cybernetics and Intelligent Systems (CIS ′10), June 2010, Singapore, 195–200, https://doi.org/10.1109/ICCIS.2010.5518556, 2-s2.0-77956072085.
10.1109/ICCIS.2010.5518556
Google Scholar
14 Smith S. M., Raeand G. J. S., and Anderson D. T., Application of fuzzy logic to the control of an autonomous underwater vehicle, 2, Proceedings of the 2nd IEEE International Conference on Fuzzy Systems, April 1993, Advanced Marine Systems Group Department of Ocean Engineering, Florida Atlantic Group, 1099–1106.
Google Scholar
15 Aouaouda S., Chadli M., Khadir M. T., and Bouarar T., Robust fault tolerant tracking controller design for unknown inputs T-S models with unmeasurable premise variables, Journal of Process Control. (2012) 22, no. 5, 861–872, https://doi.org/10.1016/j.jprocont.2012.02.016, 2-s2.0-84861648082.
10.1016/j.jprocont.2012.02.016
CAS Web of Science® Google Scholar
16 Kaminer I., Pascoal A., Hallberg E., and Silvestre C., Trajectory tracking for autonomous vehicles: an integrated approach to guidance and control, Journal of Guidance, Control, and Dynamics. (1998) 21, no. 1, 29–38, https://doi.org/10.2514/2.4229, 2-s2.0-0031673631.
10.2514/2.4229
Web of Science® Google Scholar
17 Tseng Y.-H., Chen C.-C., Lin C.-H., and Hwang Y.-S., Tracking controller design for diving behavior of an unmanned underwater vehicle, Mathematical Problems in Engineering. (2013) 2013, 10, 504541, MR3044289, https://doi.org/10.1155/2013/504541.
10.1155/2013/504541
Web of Science® Google Scholar
18 Rae G. J. S. and Smith S. M., A fuzzy rule based docking procedure for autonomous underwater vehicles, 2, Proceedings of the Mastering the Oceans Through Technology (OCEANS ′92), October 1992, IEEE, 539–546, https://doi.org/10.1109/OCEANS.1992.607638.
10.1109/OCEANS.1992.607638
Google Scholar
19 White K. A., Smith S. M., Ganesan K., Kronen D., Rae G. J. S., and Langenback R. M., Performance results of a fuzzy behavioural altitude flight controller and rendezvous & docking of an autonomous underwater vehicles with fuzzy control, Proceeding of the Autonomous Underwater Vehicle Conference, July 1996, Monterey, Calif, USA, IEEE, 117–124, https://doi.org/10.1109/AUV.1996.532407.
10.1109/AUV.1996.532407
Google Scholar
20 Passino K. M. and Yurkovich S., Fuzzy Control, 1997, 1st edition, Addison-Wesley, Reading, Mass, USA.
Google Scholar
21 de Silva C. W., Zadeh-MacFarlane-Jamshidi theorems on decoupling of a fuzzy rule base, Scientia Iranica. (2011) 18, no. 3, 611–616, https://doi.org/10.1016/j.scient.2011.04.014, 2-s2.0-80054794096.
10.1016/j.scient.2011.04.014
Web of Science® Google Scholar
22 Aguiar A. P., Nonlinear motion control of nonholonomic and underactuated systems [Ph.D. thesis], 2002, Department of Electrical Engineering, Instituto Superior Tecnico, Lisbon, Portugal.
Google Scholar

Citing Literature

All articles

Movement Control in Recovering UUV Based on Two-Stage Discrete T-S Fuzzy Model

Abstract

1. Introduction

2. Problem Statement

3. Design Scheme