Journal of Astrophysics
Volume 2014, Issue 1 193059
Research Article
Open Access

Invariant Imbedding and the Radiation Transfer in a Plane-Parallel Inhomogeneous Atmosphere

Arthur G. Nikoghossian, 

Corresponding Author

Arthur G. Nikoghossian

Ambartsumian Byurakan Astrophysical Observatory, Byurakan, 378433 Aragatsotn, Armenia bao.am

Search for more papers by this author
First published: 30 January 2014
https://doi.org/10.1155/2014/193059
Academic Editor: Milan S. Dimitrijevic
Academic Editor: Michael Kueppers
Academic Editor: Sven Wedemeyer-Bohm

Abstract

The invariant imbedding technique is applied to the problems of radiation transfer in a plane-parallel inhomogeneous atmosphere. All the parameters which describe the elementary event of scattering and the distribution of the energy sources are allowed to vary with depth. Mathematically, the considered standard problems of the theory are reduced to initial-value problems which are better adapted to capabilities of the modern high speed computers. The reflectance of an atmosphere is shown to play a prominent role in describing the diffusion process since all the other characteristics of the radiation field are expressed through it. Three transfer problems frequently encountered in astrophysical applications are discussed: the radiation diffusion in the source-free medium, in a medium with arbitrarily distributed energy sources, as well as the problem of finding the statistical mean quantities, characteristics of the multiple scattering in the atmosphere.

1. Introduction

The fast progress in observational capabilities of astrophysical instruments enables to obtain a fairly detailed picture of investigated phenomena in cosmic objects. The high-resolution spectra available nowadays afford an opportunity to study different types of inhomogeneities, the theoretical interpretation of which encounters, in general, much difficulty. Additional difficulties appear in the line-formation problems when one has to take proper account of the multiple scattering effects. This is due to coupling set in between various volumes of the radiating medium and the redistribution of radiation over frequency and directions. The classical treatment of such problems usually leads to integrodifferential equations with the conditions specified at the boundaries of the medium.

The mathematical complexity of these problems formulated for homogeneous media, stimulated to develop a variety of analytical techniques applicable to one or another specific class of the radiation transfer problems. There exists a vast literature on the field, particularly in astrophysical context. Of different methods concerning our discussion the most important is Ambartsumian’s invariance principle [1, 2], which overcomes the above difficulties by finding the requisite intensity of emerging radiation without prior knowledge of the radiation field in the entire atmosphere. An alternative approach developed by Bellman [3] and Sobolev [4, 5] is based on extensive use of the so-called “surface” resolvent function. The idea of this approach, in its turn, goes back to Kreĭn [6].

From the pioneering works treating the transfer problems is in inhomogeneous absorbing and scattering atmospheres we note here the papers by Preisendorfer [7, 8] and Busbridge [9]. Later the theory was developed by Sobolev [4, 10] and Yanovitskij [11]. The further progress of the theory is based on Ambartsumian’s method of addition of layers [1, 12] generalised by the present author [13–16] over the case of inhomogeneous media. In these papers we proposed also a new approach for solving the linear radiation transfer problems which assumes a preliminary determination of the global optical properties of an atmosphere for a family of atmospheres with different optical thicknesses. This appreciably facilitates finding of the internal field of radiation. For instance, in the simplest scalar one-dimensional case, knowledge of the reflection coefficient alone is sufficient to determine the radiation field inside the medium without solving any new equations [14].

In this paper we use the invariant imbedding technique [17–19] to inhomogeneous atmospheres with the plane-parallel geometry and reformulate the classical boundary-value problems to reduce them to initial-value problems. The numerical solution of resulting problems for integrodifferential equations is easy to obtain on the modern high speed electronic computers and, what is important, they are usually numerically stable. We show that, again, as in the scalar case, one needs to solve only one such problem for the reflectance of the medium since the other quantities of interest are found from explicit formulas.

It is important to note that under inhomogeneous atmosphere in this paper we mean an atmosphere in which any parameter defining the elementary processes of absorption and diffusion (the profile of the absorption coefficient, the probability of reradiation in scattering, and the law of redistribution of radiation over directions and frequencies as well as the role of absorption in the continuum) can vary with depth. In theoretical treatments one usually takes the averaged in some sense values of these parameters and restricts oneself to taking account of the depth-dependent distribution of the internal energy sources due to changes in characteristic thermodynamic parameters within the medium [20, 21].

The outline of the paper is as follows. We begin in Section 2 by treating the source-free problem for a plane-parallel inhomogeneous atmosphere of finite optical thickness. The case of isotropic scattering with complete redistribution over frequency is discussed for expository reason. In Section 3, we consider the problem of the radiation transfer in an atmosphere with arbitrarily distributed energy sources. It is shown that the radiation field in this case can be found without solving any new equation. Next section is devoted to statistical description of the radiation diffusion process. The mean number of scattering events and the average time of the photons diffusion in the atmosphere are found. The obtained results are discussed in the final section.

2. The Problem of Diffuse Reflection and Transmission

Consider the radiation transfer through a plane-parallel inhomogeneous atmosphere of finite optical thickness τ0 in the centre of the spectral line. For simplicity, the scattering process is assumed isotropic with complete redistribution of radiation over frequencies. We limit ourselves by assuming the depthdependence for only the scattering coefficient. The interested reader can with only small effort write down the proper equations for a more general situation. The broadening of the spectral line is generally described by the Voigt profile of the absorption coefficient α(x) = H(x, a), where a is the Voigt parameter and x is the so-called dimensionless frequency measured by the displacement from the centre of the line in the units of the Doppler widths. The normalisation factor of the Voigt function is . The role of absorption in the continuum is specified by the parameter β which is the ratio of the absorption coefficient in continuum to that in the centre of the spectral line. We introduce the notation λ(τ) for the depth-dependent probability of the photon reradiation during elementary event of scattering.

We begin by determining the global optical characteristics of the medium when it is illuminated from the side of the boundary τ = τ0 (Figure 1). We denote the azimuth-averaged reflection coefficient by ρ(x′, η; x, ξ, τ0), where x and ξ are the frequency and cosine of the angle of the incident photon and x′, η are the similar quantities for the reflected photon. It is introduced in such a way that ρ/ξ has a probabilistic meaning.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Schematic illustration of the radiation transfer in a finite plane-parallel medium illuminated from the side of boundary τ = τ0.
The function ρ satisfies the equation [22, 23]
()
where , γ(x) = α(x) + β is assumed to be independent of the optical depth,
()
and ρ(x′, η; x, ξ, 0) = 0.
Proceeding to the transmission coefficient, q(x′, η; x, ξ, τ0), we introduce the notation σ(x′, η; x, ξ, τ0) for its diffuse part, so that
()
The function σ is determined from equation
()
with
()
or
()
and σ(x′, η; x, ξ, 0) = 0 as an initial condition.

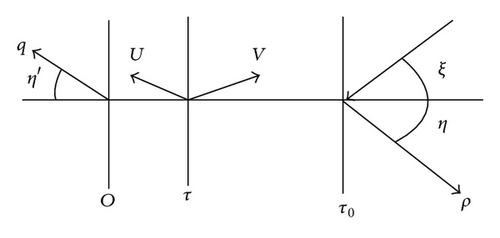
Equations (1) and (4) are obtained by using the invariant imbedding standard procedure, that is, by adding an infinitely thin layer to the boundary τ = τ0 and then letting its thickness tend to zero in the limit (see for details [14]). We use the same procedure below in obtaining the internal field of radiation.

Let us begin with the quantity U(x′, η, τ; x, ξ, τ0) which specifies the probability that the incident photon will be found after multiple scattering at depth τ as a photon within the frequency and direction intervals (x′, x′ + dx′; η, η + dη). Here, again, it is expedient to separate out its diffuse part u by analogy to that for transmission coefficient:
()
Performing the invariant imbedding procedure we arrive at
()
where
()
and u(x′, η, τ; x, ξ, τ) = 0.

It is obvious that u(x′, η, 0; x, ξ, τ0) = σ(x′, η; x, ξ, τ0) and Ψ(x′, η, 0; τ0) = ψ(x′, η, τ0), so that on solving (8) one also finds the transmission coefficient for a family of media. When one needs to determine the function u for different depths but for an atmosphere with a fixed optical thickness, that is, in order to solve the ordinary transfer equations, knowledge of the transmission coefficient makes it possible to deal again with the initial-value problem. Note also that once the reflectance of the atmosphere is determined (i.e., the function φ is known), one can use (8) to derive an explicit formula for the function u.

Now we will show that knowledge of the functions ρ(x′, η; x, ξ, τ0) and u(x′, η, τ; x, ξ, τ0) is essentially enough to find the other quantities of interest. For instance, on the base of simple physical arguments, we find
()
Up to now we have considered the case of a medium illuminated from the side of the boundary τ = τ0. Let the medium be illuminated now from the opposite side (see Figure 2). We shall see that the quantities ρ and u found above fully determine the optical characteristics and the internal field of radiation also in this problem (the quantities applying to this case will be supplied by an overhead bar). For example, the invariant imbedding method leads to the following equation for the reflection coefficient :
()
with the initial condition . It is easily seen that solution of (11) is reduced to computing the ordinary integral. As for the transmission coefficient, the reversibility principle of optical phenomena implies .
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Schematic illustration of the radiation transfer in a finite plane-parallel medium illuminated from the side of boundary τ = 0.
The radiation field inside the medium found with the same method is reduced to computing simple integrals. For instance, the function , which specifies the intensity of radiation directed to the boundary τ = 0, satisfies equation
()
with the initial condition . Here again, since the right-hand side of (12) is known, its solution is equivalent to computing the following integral:
()
Knowledge of allows, in its turn, finding the last of requisite quantities yielding the intensity of radiation in the opposite direction:
()
This completes the solution of the source-free problem. We saw that this requires solving only two initial-value problems (1) and (8) for integrodifferential equations. Let us turn next to the solution of another problem frequently encountered in astrophysical applications.

3. Internal Energy Sources

Once the problem of diffuse reflection and transmission is solved, one may obtain much easier the solution of another standard problem concerning the radiation field in an atmosphere containing energy sources. One of the various parameters whose distribution influenced the observed spectra is the power of the internal energy sources, which are specified by the values of thermodynamic parameters and are generally distributed nonuniformly in the atmosphere. Thus, the problem of determining the effects of an inhomogeneous distribution of the internal energy sources naturally arises in any realistic astrophysical problem of the spectra interpretation.

Consider a three-dimensional plane-parallel and inhomogeneous atmosphere of finite optical thickness containing energy sources of the power B(τ, x, η). We denote the intensities of radiation emerging from the medium through the boundaries τ = τ0 and τ = 0 by I1(x, ξ, τ0) and I2(x, ξ, τ0), respectively. These quantities are easy to find taking into account the reversibility principle of the optical phenomena applied to the functions U and V, which now can be interpreted as the probabilities that the photons moving at the depth τ to the right and to the left in Figure 1 will escape the atmosphere from the boundary τ = τ0. Then we may write
()
where W = U + V; that is,
()
Similarly, having in mind the alternative probability meaning of the functions and , we find
()
where
()
We now proceed to the problem of determining the radiation field inside the treated atmosphere. To this end, we introduce the notation I−(x, η, τ; τ0) for the intensity of radiation of frequency x at the optical depth τ directed to the boundary τ = 0 at the angle cos −1η. Similarly, the intensity directed to the boundary τ = τ0 is denoted by I+(x, η, τ; τ0). The angles in both cases are referenced from the normal to the corresponding boundary. The customary invariant imbedding procedure yields
()
with the condition I−(x, η, τ;   0) = 0. It is discernable that all the quantities appearing in the right-hand side of (19) are known so that the problem is simply reduced to calculating of the ordinary integral.
Once I−(x, η, τ; τ0) is known, it is easy to find the last of the requisite quantities, I+(x, η, τ; τ0), since they are related by a simple formula with an obvious physical significance:
()
Thus, solving the diffuse reflection and transmission problem of the preceding section is an important prelude to solving the radiation transfer problem in atmospheres containing energy sources. Finally, we remind that the approach used here provides a solution to the problem for a family of atmospheres of different optical thicknesses.

4. The Statistical Description of the Radiation Diffusion

In treating different astrophysical problems, one often needs to estimate various statistical averages characterizing the radiation diffusion in an atmosphere. This facilitates better understanding of the physical essence of a number of effects predicted by the mathematical solution of the problem. The statistical investigation of multiple scattering makes it possible to determine a number of important physical characteristics of an atmosphere such as the mean radiation density and the mean degree of excitation of the atoms. One of the important statistical averages is the mean number of scattering events (MNS) underwent by the photon during its travel in the atmosphere. Of the extensive literature on this topic we mention here Ambartsumian’s pioneering work [1, 24], in which for determining this quantity for homogeneous atmosphere the following formula was proposed:
()
where I is the radiation intensity. As it was shown in [25], this formula is valid for any flux of “moving” photons (i.e., not for those subsequently destroyed in the medium). The problem of estimating the MNS in the case of inhomogeneous media was examined in [14], and it was shown that the procedure of the formal differentiation over λ remains in force also in this general case despite the fact that now the scattering coefficient varies with depth. This may be concluded by observing the way this function enters in the proper equations.
Consider, for instance, the statistics of multiple scattering of the photon of frequency x incident on the boundary τ = τ0 of the medium at the angle cos −1ξ. We are interested in the MNS for three types of photons: reflected, transmitted, and destroyed in the medium independent of their final frequency and direction. Denoting the probabilities for each of these processes by , , and , it easy to derive from (1)–(4)
()
()
()
where we have introduced the notations
()
Once (1), (4) (or (8)) are solved, the zeroth moments of the functions φ and ψ can be regarded as known. To solve (24), we need to find also ϕ0(τ0). One can easily derive Volterra-type integral equation for this function from the same (24):
()
where the kernel-function L given by
()
is well known in the radiative transfer theory and
()
()
Further, the formal differentiation of (22) and (23) over λ allows obtaining separate equations for the expected number of scattering events, N*(x, ξ, τ0), N0(x, ξ, τ0) corres-pondingly for the reflected and transmitted photons:
()
where f(x, ξ, τ0) = λ∂φ(x, ξ, τ0)/∂λ, f0(τ0) = λ∂φ0(τ0)/∂λ, and g0(τ0) = λ∂ψ0(τ0)/∂λ. As the initial conditions, we have N*(x, ξ, 0) = N0(x, ξ, 0) = 0. The ratios and obviously give the requisite MNS for the reflected and transmitted photons.
Let us turn further to the photons which are destroyed in the course of multiple scattering in the atmosphere. The invariant imbedding technique must be now applied by counting the number of scattering events for each elementary process appearing in adding a complementary layer to the initial medium. The generating function approach developed in [25] allows finding the expected number of scattering events, Na, for this type of photons from
()
where h0(τ0) = λ∂ϕ0(τ0)/∂λ and the initial condition is Na(x, ξ, 0) = 0. It is readily seen that 〈N〉 = N* + N0 + Na represents the MNS for the photons of frequency x incident on the medium at the angle cos −1ξ irrespective of whether or not they are subsequently destroyed in the medium or leave it.  Taking into account that and  and introducing the notation
()
we arrive at
()
with the initial condition 〈N(x, ξ, 0)〉 = 0.
As above in the case of (24), we deal with the similar initial-value problem which can be solved if only the zeroth moment Φ(τ0) is determined. It is easy to show that this function satisfies integral equation (26) with the only difference that now the free term is
()
where the functions L and F are given by (27), (29).

We see that knowledge of only reflection function is sufficient to find the MNS for all the incident photons independent of their future “fate.” Equations (24), (25) easily yield the numerical solution. Some analytical results can be obtained in the specific case of homogeneous medium [25, 26], for which all the above-introduced functions dependent on frequency and direction are, in fact, the functions of the combined variable γ(x)/ξ. Note also that taking derivatives in these equations to zero we are led to the results previously derived in the mentioned paper for semi-infinite media. Comparing (33) and (24) for β = 0, that is, neglecting the role of absorption in continuum, we find .

Let us pursue our considerations further and apply the same approach to determine the continuously distributed random quantities describing the radiation diffusion. As an illustration, we consider here the problem of finding the average time spent by the photon on multiple scattering in the medium. Because of the important role which this statistical mean quantity plays in astrophysical applications, it was a subject of investigations by a number of researchers [27–30]. In the general case, when the photons are destroyed not only during scattering but also in flight, this average makes it possible to gauge the relative importance of the energy dissipation in the medium and its flow through a boundary. Another important application of this average is associated with the problem usually arising in the presence of the nonstationary sources of energy in atmosphere, when one needs to reveal whether the radiative equilibrium is established or not [31].

Turning directly to our problem, we note that mathematically the only case of interest is that for which the photon spends time only on travelling the path between two successive scattering events. With regard to the mean time spent by the diffusing photon while the atoms are in the excited state, it can be taken into account when necessary by simple multiplication of the MNS and the average time required by each of the atoms for the reemission process. This is admissible because these two random variables are statistically independent.

For convenience, we will measure the time intervals in the units of , where n is the number of scattering particles in 1 cm3 and is the absorption coefficient in the centre of the line, calculated for one atom. It is easy to see that t represents the time required to travel the mean free path between two successive scattering events for a photon in the line centre if there is no absorption in continuum. We denote the dimensionless time by ω. In determining the time averages, we, again, as above, consider three types of photons: reflected, transmitted, and destroyed in the course of multiple scattering. Here we confine ourselves to relatively detailed treatment of the problem for the first of these categories of photons. In the case of two other types, we present only the final results.

Starting with the process of reflection, let us introduce the generalised reflection coefficient which is the time-dependent analogue of that defined in Section 2 and concerns the photons reflected in the time interval (ω, ω + dω). Invariant imbedding approach allows to write
()
where δ is the Dirac δ-function.
The method of characteristic functions applied to this equation is equivalent to performing the Laplace transformation [27]. For the Laplace transform of the time-dependent reflection coefficient
()
one can write
()
where
()
Taking s = 0, we go back to (1). For finding the required average time for reflected photons, we need the derivative Ω*(x, η; x, ξ; τ0) = dT/ds|s=0. It follows from (37) that
()
where
()

It is not difficult to show that this equation can be obtained by formal differentiating (1) with respect to β and exchanging the sign. Similar result for homogeneous atmosphere was obtained for the first time in [27]. Thus, now we arrive at an important generalization of this result by showing that it remains valid also for inhomogeneous media. As above in the case of MNS, the differentiation procedure holds true only for reflected and transmitted photons. It is obvious that the ratio Ω*/ρ gives the detailed information on the average time spent by reflected photons dependent on their initial and final frequency and directional characteristics.

We are interested here by the average time, , spent by all the reflected photons irrespective of their final frequency and direction. Integration of (39) over x′ and η yields
()
where and .
By analogous manner we obtain the mean expected time for all the transmitted photons if the boundary τ = τ0 of the atmosphere is illuminated by photons with (x, ξ) characteristics:
()
where and the initial condition is .
As for the photons destroyed in the atmosphere, derivation of appropriate equation for the expected time Ωa cannot be found by direct differentiation and must be obtained by employing the imbedding technique. As a result, we obtain
()
where we introduced notations and the initial condition . Once (41)–(43) are solved, the ratios , , and give the requisite values of the average time for three categories of photons. Further, represents the average time for incident photons diffusion in the atmosphere irrespective of whether they escape from the medium or are destroyed in it. From (41)–(43) we obtain
()
where
()
and initial condition 〈Ω(x, ξ, 0)〉 = 0. As for the function , it satisfies integral equation (26) with the free term G(τ0) = βF(τ0).

Equation (44) implies that again, as in the case of MNS, knowledge of the reflection coefficient alone ensures the temporal description of the diffusion process in the atmosphere. In fact, solution of similar initial-value problems for integrodifferential equations gives a detailed statistical description on the multiple scattering in inhomogeneous media. As it was pointed out, in the treated special case of completely incoherent scattering, the form of the proper functions and equations can be simplified by introducing the combined variables of the γ(x)/ξ type. However, we give preference to separation of these arguments, which is better suited for numerical calculations. Note in conclusion that in the particular case of homogeneous media comparison of (24), (33), and (44) yields the well-known relation between different statistical mean quantities .

5. Concluding Remarks

We discussed two frequently encountered model problems of the radiative transfer in a plane-parallel inhomogeneous medium and showed that they can be mathematically reduced to the solution of only one initial-value problem for integrodifferential equations for reflectance (1) with the subsequent evaluation of several ordinary integrals. This allows overcoming the well-known difficulties specific to the boundary-value problems, to which the classical formulation of the physical problems usually leads. For simplicity, the inhomogeneity of the medium was explicitly indicated only in the scattering coefficient, while all other parameters controlling the elementary scattering and absorption processes can be also allowed to be dependent on optical depth. All the requisite quantities are found for a family of atmospheres of different optical thicknesses.

The same approach was applied in finding the MNS and the average time of the photons travel in the medium for different types of photons. Solution of the resulting integrodifferential equations gives the detailed statistical description of the radiation diffusion process depending on the angular and frequency parameters of the incident, reflected, transmitted, and destructed photons. The statistical mean quantities are of special interest for applications concerning all the diffusing photons independent of that whether they are destroyed in the medium or escape from it. These quantities are completely determined by the reflection properties of the medium. It is apparent that by analogous manner one can find the statistical averages for any discretely or continuously distributed random quantities describing the radiation diffusion process.

Summarizing the results obtained in the paper we observe that the starting point in all of the considered problems is the determination of the reflectance of an atmosphere. In other words, knowledge of only the reflection coefficient makes it possible to gain complete insight into the field of radiation inside the medium and the statistical properties of the diffusion process. This is of great importance in view of that this coefficient is defined from a separate equation and that it is an observable and measurable quantity in contrast to the source function which plays an important role in the classical theory of the radiative transfer. In fact, the obtained results can be regarded as a generalization, in some sense, of Ambartsumian’s invariance idea to the finite inhomogeneous atmosphere.

From pure mathematical point of view, the proposed approach facilitates solving the traditional and frequently used model problems to a large extent. It is based on obvious physical arguments, so it is intuitively clear, universal, and easy to use.

Conflict of Interests

The author declares that there is no conflict of interests regarding the publication of this paper.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.