Discrete Dynamics in Nature and Society
Volume 2014, Issue 1 174927
Research Article
Open Access

Smolyak-Grid-Based Flutter Analysis with the Stochastic Aerodynamic Uncertainty

Yuting Dai, 

Corresponding Author

Yuting Dai

School of Aeronautic Science and Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100191, China buaa.edu.cn

Search for more papers by this author
Chao Yang, 

Chao Yang

School of Aeronautic Science and Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100191, China buaa.edu.cn

Search for more papers by this author
First published: 23 March 2014
https://doi.org/10.1155/2014/174927
Citations: 2
Academic Editor: Guanghui Wen

Abstract

How to estimate the stochastic aerodynamic parametric uncertainty on aeroelastic stability is studied in this current work. The aerodynamic uncertainty is more complicated than the structural one, and it takes more significant effect on the flutter boundary. First, the nominal unsteady aerodynamic influence coefficients were calculated with the doublet lattice method. Based on this nominal model, the stochastic uncertainty model for unsteady aerodynamic pressure coefficients was constructed with physical meaning. Afterwards, the methodology for flutter uncertainty quantification due to aerodynamic perturbation was developed, based on the nonintrusive polynomial chaos expansion theory. In order to enhance the computational efficiency, the integration algorithm, namely, Smolyak sparse grids, was employed to calculate the coefficients of the stochastic polynomial basis. Finally, the flutter uncertainty analysis methodology was applied to an aircraft′s wing model. The influence of uncertainty with uniform distribution for aerodynamic pressure coefficients on flutter boundary was quantified. The numerical results indicate that, the influence of unsteady aerodynamic pressure due to the motion of coupling modes takes significant effect on flutter boundary. It is validated that the flutter uncertainty analysis based on Smolyak sparse grids integration is efficient and accurate for quantifying input uncertainty with high dimensions.

1. Introduction

Flutter is an aeroelastic instability phenomenon, which involves the interaction of elastic structures, aerodynamic force, and inertial force. Though with high fidelity, the definite models to describe aeroelastic behavior of real aircrafts and missiles are so complicated that uncertainties or nonlinearities are inevitable. Pettit summarized the results and advances about uncertainty quantification in aeroelasticity [1] extensively. This academic paper is focused on the study of aeroelastic stability, response, and design problems with uncertainties. Most of the research topics can be classified into two aspects, either probabilistic aeroelasticity or nonprobabilistic one. For the nonprobabilistic aeroelasticity, it is of no need to know the probabilistic distributions of the uncertainties for input physical parameters and output aeroelastic response [2]. In addition, the extreme range of aeroelastic response is paid attention to, namely, “worst case” or “robust” [3]. Sometimes, the robust flutter boundary may be overconservative as there is “bad experimental data.” This is why aeroelastic analysis with probabilistic uncertainty comes into our mind. For probabilistic aeroelasticity, both the input and output uncertainties are characterized as random variables. This is originated from the areas of structure reliability analysis and system engineering. The Monte Carlo Simulation (MCS) [4, 5], the Polynomial Chaos Expansion (PCE) [6], and the Stochastic Collocation [7] methods are the well-known theories in probabilistic uncertainty quantification. However, whether they are applicable in flutter uncertainty quantification is not clear. Generally, among the three methods, MCS is regarded as the straightforward choice for uncertainty quantification of probabilistic aeroelasticity. The influence of uncertainty for structural parameters on flutter boundary was analyzed by Pitt et al. [8]. In particular, he strongly recommended that uncertainty margin should be introduced into aircraft certification process. When we are applying computational fluid dynamics to calculate the unsteady aerodynamics, MCS may increase the computational time rapidly [1, 9]. Hence, the potential of PCE method was tremendous in the field of computational aeroelasticity due to its high efficiency. In this method, the uncertainties of inputs and outputs of aeroelastic system are projected into a stochastic space. Pettit et al. successfully applied the PCE method to the analysis of aeroelastic limit cycle oscillations [10, 11]. The stochastic basis construction of the PCE method for harmonic oscillations is an outstanding contribution in his research. The advantage and drawback of MCS and PCE were compared thoroughly by Badcock et al. [12]. However, the present research of stochastic uncertainty quantification in aeroelasticity is mainly determining the effect of the structural uncertainty on aeroelastic stability. However, few of published works are about the uncertainty modeling and quantification of unsteady aerodynamics. Due to the importance of unsteady aerodynamics on flutter boundary, the effect of stochastic aerodynamic uncertainty on flutter velocity will be studied and quantified in the present work. First, the stochastic uncertainty model of aerodynamic pressure in the frequency domain was constructed. Combined with the widely used pk method, the nonintrusive PCE method is developed to analyze the influence of aerodynamic uncertainty on flutter boundary. Since the dimension of aerodynamic uncertainty is moderately large, the computational time of full tensor-product integration increases exponentially. Hence, the modified numerical integration method, namely, Smolyak sparse grids numerical integration algorithm [13], is developed to calculate the formulation of uncertain flutter boundary. Finally, a numerical example of aircraft’s wing model is applied to validate the flutter uncertainty quantification framework.

2. Nominal Flutter Solution: pk Method

When there is no external force, the generalized aeroelastic equation of motion without uncertainty can be written as
()

The above aeroelastic equation is represented under the system of the modal basis coordinates. q represents the modal coordinate vector. M0,  C0, and K0 are the generalized mass, damping, and stiffness, respectively. Q0 is the generalized unsteady aerodynamic influence coefficients. It is related to the Mach number Ma and the reduced frequency k. represents the dynamic pressure and V is the free-stream velocity.

Equation (1) is a characteristic equation essentially. However, it is not so easy for the flutter solution since Q0 is related to the discrete reduced frequency but not a continuous known formulation. How to calculate it accurately in the frequency domain is important to flutter analysis. The pk algorithm is widely used in flutter solution for engineering applications, to solve the above characteristic equation [14]. For the algorithm, it is assumed that
()
where p = ω(γ + i) is the complex eigenvalue. As we know, at the flutter velocity condition, the damping is zero and the aircraft is critically undergoing a harmonic oscillating. Hence, the unsteady aerodynamic force is also assumed to be oscillating with flutter frequency. Then, the modified flutter equation can be written as
()
where the reduced frequency is k = ωb/V = (b/V)Im⁡(p)  and  b  is the half of chord length.
The characteristic equation of (3) can be rewritten in a standard form:
()
where
()

The procedure of flutter solution with pk algorithm is as follows, given the flight velocity Vand an initial value of k, for each mode, solving the characteristic equation of (4) to obtain an eigenvalue p. Comparing its imaginary part of p with k, iterating the above equation until the discrepancy between the imaginary part of p and k is small enough. Then, the frequency and damping are obtained at this given flight velocity V. The same procedure is repeated for several velocities. The flutter velocity Vf and frequency ωf will be reached with the zero damp at a certain velocity.

3. Stochastic Uncertainty Model for Aerodynamics

In order to solve the flutter problem in (1), the determination of the unsteady aerodynamic force due to elastic motion in a discrete frequency domain is essential to us. The linear doublet lattice method (DLM) is well accepted by the aerospace industry and widely employed in aeroelastic applications to calculate the unsteady aerodynamics, since it can handle configurations without extensive time for most subsonic aircrafts. It relates motions of the dynamic down wash to the pressure coefficients for each aerodynamic panel, based on unsteady linear small-disturbance equations for fluid dynamics. Three different calculation architectures can describe the unsteady aerodynamic model in DLM scheme. Those are the models for aerodynamic influence coefficients (AIC matrix), the aerodynamic pressure coefficients (Cp matrix), and the generalized aerodynamic influence coefficients (GAIC matrix) indicated in (1). In fact, all the three aerodynamic descriptions should be transformed to the GAIC form. However, we can investigate in more details with the first two descriptions. Nowadays, only the Cp matrix can be measured in the wind tunnel test. Hence, the nominal aerodynamics together with its uncertainty model should be constructed in the Cp architecture. Based on this consideration, the generalized aerodynamic force (denoted as GAIC) in (1) is rewritten as
()
where Φp is the modal matrix of the pressure nodes on the aerodynamic planar elements. represents the diagonal matrix composed of area for each planar element.  nA is the total number of devised aerodynamic planar elements. represents the dynamic pressure coefficients on aerodynamic elements due to harmonic modal motion, at given reduced frequency k. NM is the number of normal modes for the structural dynamics.

3.1. Uncertainty Model for Aerodynamic Pressure Coefficients

Considering the numerical error of the unsteady pressure coefficients Cp(Ma,  ik), (6) can be rewritten as
()
where the Wcpl and Wcpr represent the left and right weighting matrixes for pressure coefficient uncertainty, respectively. They scale the pressure perturbation such that the stochastic uncertain variables ξi in Δcp are subject to certain distributions in [−1,1]. For simplicity, all the uncertainties are independent and identically and uniformly distributed.
Usually, the weighting matrixes of Wcpl and Wcpr should be verified by experiments or accurate data with high fidelity model. Afterwards, the generalized aerodynamic force with uncertainty is reformulated as follows:
()
If the matrix of Δcp is a full nonzero matrix, there will be nA × NM stochastic uncertainties in the input parameters. Too many uncertain variables will increase the complexity of the problem. In order to reduce the number of uncertain input variables, we assume that, for every normal vibration mode, the relative pressure coefficients on different aerodynamic panels perturb in a uniform manner. By this assumption, the perturbed pressure coefficient ΔCp(j, i) on each aerodynamic panel j for every mode i can be represented as
()
That is to say, after the scaling of w, ξcpi = 1 means that the perturbed pressure coefficients on different patches j and k will reach their largest values Cp0(j, i)wj,i, Cp0(k, i)wk,i simultaneously. Under this hypothesis, the number of independent aerodynamic uncertainties, denoted by nδ, equals NM. Comparing (8) with (9), it is clear that . In this case, the left and right weighting matrixes are as follows:
()

With this uncertainty model, it is easy to understand the physical meaning of aerodynamic perturbation manner. Moreover, its uncertainty distribution may be measured by the wind tunnel test. The advantage of introducing the hypothesis is that the uncertainty size is much less than the aerodynamic panels in most general cases. This handling can reduce much time in the numerical calculation. However, the drawback is that the pressure coefficients on all patches are perturbed in the same manner.

3.2. Analysis of Flutter Uncertainty

Since parametric uncertainty exists in the aerodynamic model, the flutter boundary solved by (1) will also be a random variable. Similar to the nominal harmonic assumption for motions at the flutter velocity, the random response q(ξ(θ), t) can also be written in an exponential form as follows:
()
Comparing (2) with (11), the modal motion in the frequency domain is written as a series of random polynomials, where Pj(ξ(θ)) is the jth polynomial basis and is the random input vector. qj represents the modal vector of the jth polynomials in the frequency domain.
Substituting both of the input uncertainties of aerodynamics and output random response of motion into (1), the uncertain flutter equation can be rewritten as
()
where , i = 1,2, …, Np. . Np is the total number of items for stochastic polynomials. With total-order expansion strategy for multidimensional uncertainties, Np is written as
()
where P is the polynomial order bound for the one-dimensional uncertainty. Comparing (12) with the nominal flutter equation of pk method, the uncertain characteristic equation can be rearranged as
()
where
()
We can clearly see that matrix As contains the stochastic uncertain variables ξ(θ), different from the nominal A0 in (5). If the stochastic parametric uncertainties are given by random sampling, we can also utilize the pk algorithm in Section 1 to calculate the flutter boundary one sample by one sample. It is straightforward but time consuming. In this case, the individual flutter velocity is associated with the stochastic parameter’s uncertainty, and the distribution of flutter velocities can be obtained by estimating the statistic measurement of all the samples. Regardless of the calculation time of the sampling-based method, it is appropriate and straightforward for flutter uncertainty quantification. However, for large engineering problems, the computational time may be too long to employ. Except for the standard MCS method, similar to the stochastic form for motion response q(ξ(θ), t), the flutter velocity is also written as a series of stochastic polynomials; that is,
()
where is the coefficient of stochastic polynomial basis.
This type of polynomials should be selected according to the probability distribution of the input uncertainties. Note that when the stochastic uncertainty satisfies a uniform distribution located in the range of [−1,1], the Legendre polynomials are orthogonal within the probability density function. The formulation of one-dimensional Legendre polynomials is written as
()
The orthogonality property for one-dimensional Legendre polynomials is written as
()
where Lj is jth constant for orthogonality and δmj is the Dirac constant. It is obvious that Lj is 1 at m = j and is 0 for other m-j pairs. Multiplication by the jth polynomial basis in two sides of (16) and integration result in determining as follows:
()

After the coefficients of polynomial basis are calculated, is substituted into (16). Hence, the relationship of flutter velocity and aerodynamic uncertainty can explicitly be represented. Consequently, the influence of aerodynamic parametric uncertainty to aeroelastic stability can be quantified, which helps engineers make reasonable decision of aircraft design.

3.3. Numerical Integration of Smolyak Sparse Grids

In order to solve the flutter equation of (14) with uncertainty, the coefficients of polynomial basis in (16) should be estimated by (19) firstly. In this section, we will develop an algorithm to calculate the numerical integration in the numerator efficiently.

For discrete function, we have several methods for numerical integrals with high dimensions. Those include the sampling-based MCS method, the point collocation method, and the full tensor-product numerical integration one. MCS is to sample the uncertainty within the density of the weighting function and to calculate the expectation of the response-basis product. It is different from the above direct MCS for response. The MCS here is only employed for determining the coefficients of polynomials not to quantify the flutter uncertainty directly. The point collocation method, known as stochastic response surfaces method, solves a least square response equation to best match the response values. It is more feasible than the MCS method since its number of collocation points is much less [15]. The extension of tensor-product for one-dimensional quadrature is a direct approach to estimate the multidimensional integrals in (19) for several uncertainties.

As an extension, the multidimensional integrals by full tensor-product in (19) is written as
()
where is the integration weight coefficient, is the jnth integration point for the inth uncertainty, and min is the total number of points for inth uncertainty. From (20), it can be seen that the inner product needs multivariate integration of the uncertainties, and the total number for tensor-product function evaluations is . It is feasible for integrals when the number of uncertainties and the number of collocation point in each direction are small. Usually, we can limit the collocation point for each uncertainty to get an acceptable accuracy. However, the uncertainty size is beyond our manipulation. It depends on the specific problem. It is easy to understand that the number of evaluation points grows exponentially with the size of uncertainties. Hence, the approximations based on tensor-product grids may suffer from the curse of dimensionality, which limits its application to complicated engineering problems. Therefore, the numerical integration of Smolyak sparse grids is developed to solve “dimension catastrophe.” It is originated from the full tensor-product, but it reduces the number of integral points, while preserving a high accuracy [13]. Motivated by this advantage, the effective Smolyak sparse grid integration method is developed along with flutter analysis algorithm, for high dimensional uncertainty quantification.
The Smolyak sparse grid integration is modified according to the full tensor-product. Note that a given level lw is introduced for different integration points. It is independent of the uncertainty dimension. By the transformation, the numerical integration formula of Smolyak sparse grids can be written as [16]
()
where |i| = i1 + i2 + ⋯in is the summation of all the uncertainty indexes. V0ξ is evaluated with flutter solution at each integration point. The significant difference of Smolyak sparse grid and full tensor-product is the choice of integration points. Here, the common nonlinear Clenshaw-Curtis integration formula is used for point number at each direction. The number of integration points in one dimension is given as follows:
()
where i is the index. When the collocation point of integration is the roots of polynomial basis of order p, the accuracy of numerical integration is 2p.

From the comparison of (20) and (21), it can be seen that the Smolyak sparse grids integration only accounts for the collocation point whose index is between lw + 1 and lw + NM. It can significantly reduce the number of integration points to improve the computational efficiency.

4. Numerical Example

An aircraft’s wing model is selected to validate the flutter uncertainty analysis. Its structure and finite element model are shown in Figure 1. The finite element model is used to calculate the model’s modal frequencies and modal shapes. Its aerodynamic model is based on the subsonic DLM. When the aerodynamic uncertainty is not considered, the flutter velocity of the wing model is 36.8 m/s and the frequency is 5.71 Hz by the nominal pk method. The velocity-frequency plot shows that the coupling of the wing’s second bending mode and the first torsion mode results in occurrence of flutter phenomenon.

Details are in the caption following the image
Figure 1 (a)
Open in figure viewerPowerPoint
Structure and its finite element model for a wing.
Details are in the caption following the image
Figure 1 (b)
Open in figure viewerPowerPoint
Structure and its finite element model for a wing.

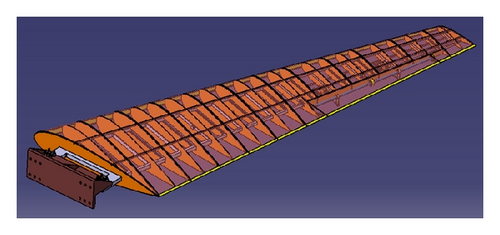
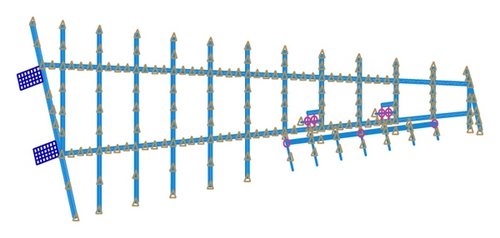
Afterwards, the stochastic uncertainty for the aerodynamic pressure is considered to quantify flutter uncertainty. Here, the uncertainty level wi of 0.1 is given for the aerodynamic pressure coefficients. It means that the calculation error of the aerodynamic force due to the modal motions may be up to 10% of their nominal values. The four parametric uncertainties are described as random variables with independently uniform distribution.

First, the MCS is employed to simulate the distribution of flutter velocities [17] numerically. It is regarded as a criterion and a basic method for comparison. 10000 random samples are simulated on a Thinkpad T430 laptop with computational time of 4814 seconds. The simulation error for MCS is 1%, approximated with the sampling number [16]. According to the statistic data of these input and outputs samples, the mean value of flutter velocity is 36.5 m/s with its standard error of 0.7905 m/s. In this specific random simulation, the flutter velocity scatters from 35.1 m/s to 38.3 m/s.

Our objective is to enhance the efficiency of flutter uncertainty analysis. Hence, the PCE approach along with different integration algorithms was applied for comparison. A straightforward PCE approach is to utilize the MCS simulation results. Naturally, the stochastic aerodynamic samples and flutter velocities obtained by the MCS above were employed to estimate the coefficients of polynomial basis in (16). Therefore, the flutter uncertainty can be represented explicitly by the stochastic polynomials, whose stochastic data is shown in Table 1, compared with different orders of Legendre polynomials.

Table 1. Flutter uncertainty by the PCE method.
One-dimensional polynomial order P Mean value for flutter velocity: m/s Standard error for flutter velocity: m/s Velocity range: m/s
1 36.5 0.7835 [35.0, 38.1]
2 36.5 0.7840 [35.1, 38.2]
3 36.5 0.7877 [34.9, 38.2]
4 36.5 0.7987 [34.8, 38.3]
5 36.5 0.8137 [34.5, 38.6]

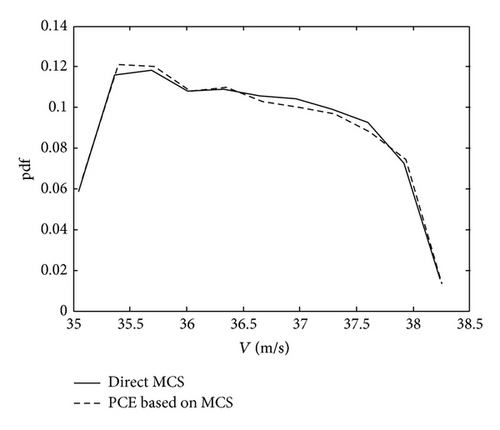
From Table 1, we can conclude that the stochastic polynomials with only one order are accurate enough to depict the flutter uncertainty. And the coefficients for polynomials of high order are not so accurate since the velocity range in the third column of Table 1 became larger with the order of polynomials increasing. It infers that the sampling-based PCE method does not always converge with high order of polynomials. With one-order stochastic polynomials, the statistical distribution for flutter velocity is shown in Figure 2. From the comparison of the results by MCS and PCE, the two probability density functions agree well with each other. Consequently, in the following, the polynomials of one order are employed for more detailed investigation.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
The probability density for flutter uncertainty by MCS and PCE.
By means of the PCE method with coefficients estimated by the MCS, we can write the formulation for flutter uncertainty of velocity explicitly as follows:
()

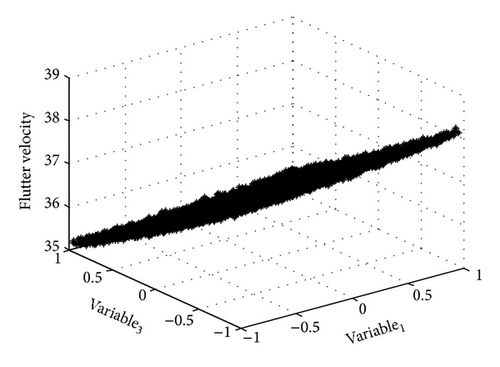
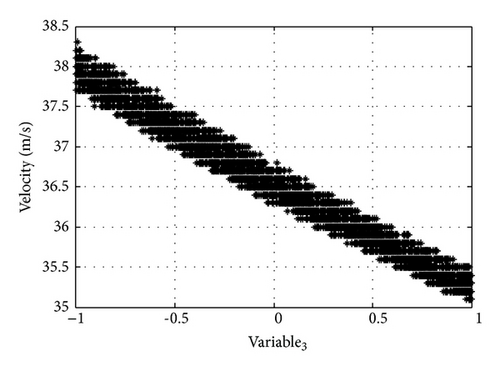
From the above equation, it is clear that the aerodynamic uncertainty due to the third modal motion, that is, the torsional mode, has significant effect on the flutter boundary. While the aerodynamic uncertainties of the second and forth modes have little effect on flutter boundary. This property can also be seen from Figures 3 and 4. In Figure 3, the flutter velocity is nearly a surface, which decreases with the aerodynamic pressure due to the torsional mode. Therefore, in order to get a high accuracy of flutter boundary, we should improve the accuracy of aerodynamics of key modes, such as the torsional mode in this example.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
The statistic distribution of flutter velocity.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
The statistic distribution of flutter velocity with the uncertainty of 3rd aerodynamic pressure coefficient.

The above flutter uncertainty quantification is essentially based on random sampling, either by the standard MCS approach or by the PCE method. For this simple wing model, we still need 4814 seconds to complete flutter uncertainty quantification, let alone a complicated full aircraft model.

In this section, the numerical integration algorithm instead of random sampling is employed to calculate the coefficients of the flutter polynomial basis in (16). First, the full tensor-product integral is conducted with 6-order polynomials. In order to achieve a high accuracy of the coefficient, the integration points are located at the roots of the Legendre polynomials. In this case, from (20), there will be 64 flutter evaluations for the full tensor-product method. 1296 eigenvalue solutions were obtained with the computational time of 481 seconds. After the coefficients of polynomials were calculated, the flutter uncertainty can be written as
()

From the comparison of (23) and (24), it can be seen that the coefficients with the two approaches agree well with each other. In addition, the computational time (481 s) reduces much, compared with the results by MCS-based PCE method (4841 s). The results indicated that the PCE based on full tensor-production is more advantageous than the one based on MCS sampling.

In order to further reduce the computational time for numerical integration, the Smolyak sparse grids were employed to reduce the collocation points. In this wing’s example, the grid level lw = 2 was selected. According to (21), 83 collocation points of flutter solution should be calculated. From the roots of Legendre polynomials and Clenshaw-Curtis formula, we first determine the integration point and weighting coefficients of Smolyak grids. Then, at each integration point, the flutter equation will be solved by the pk algorithm, to calculate the individual flutter velocity. From the PCE analysis above, it is known that the polynomials of one order are enough for a good accuracy. Consequently, the coefficients of polynomials in Smolyak grid method are calculated, and the uncertainty of flutter velocity is written as
()

The flutter uncertainty formula by Smolyak sparse gird is completely the same as the one by the full tensor-product approach. Notably, the computational time of Smolyak sparse grid is only 35 seconds. It significantly reduces the computational time while preserving the accuracy.

5. Conclusions

The stochastic uncertainty model for unsteady aerodynamic pressure coefficients is constructed in this paper. Based on the uncertainty model, the polynomial chaos expansion method based on Smolyak sparse grid is developed in the analysis of flutter uncertainty. The flutter uncertainty formula due to aerodynamic uncertainty can be obtained with high efficiency. By the comparison of accuracy and efficiency of three different approaches, it indicates that the PCE with Smolyak sparse grids is advantageous for flutter uncertainty quantification. By the validation of a wing’s example, the following is concluded.
  • (1)

    It is feasible to construct uncertainty model for aerodynamic pressure coefficients which has physical meaning. The aerodynamic accuracy of key mode is vital for flutter boundary. Its calculation accuracy should be paid much attention to.

  • (2)

    The PCE method together with Smolyak sparse grids is applicable for aeroelastic stability analysis and especially suitable with high dimensional uncertainties. It can improve the efficiency of uncertain aeroelastic analysis, which is helpful for flutter uncertainty quantification of full aircrafts.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (nos. 11302011 and 11172025) and the Research Fund for the Doctoral Program of Higher Education of China (no. 20131102120051).

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.