The aim of this paper is to extend the lattice method proposed by Ritchken and Trevor (1999) for pricing American options with one-dimensional stochastic volatility models to the two-dimensional cases with strangle payoff. This proposed method is compared with the least square Monte-Carlo method via numerical examples.

1. Introduction

Calculating American style options under geometric Brownian motion is far from the realistic financial market. It is more valuable to price American style options under stochastic models. In general the valuation of American options with stochastic volatility models has no closed-form solution except very few cases (see, e.g., Heston [1]). Therefore numerical methods or simulation methods are developed to price financial derivatives with stochastic volatility, among which the lattice methods receive much more attention. Ritchken and Trevor [2] proposed an efficient lattice method for pricing American options under GARCH models. Later the idea was further developed and applied by several papers, for example, Cakici and Topyan [3] and Wu [4], and recently the convergence of the method was proved by Akyildirim et al. [5].

All the abovementioned references focused on the development of lattice methods for pricing American options with one underlying asset and single stochastic volatility model. To the best of our knowledge, there are no papers studying the lattice methods for options with many underlying assets and multidimensional stochastic volatility models. Indeed there are many papers in developing lattice methods for pricing options with many underlying assets, for example, Boyle [6], Boyle et al. [7], Chen et al. [8], Gamba and Trigeorgis [9], and Moon et al. [10]. However it is not seen for lattice methods for multidimensional stochastic volatility models.

In this paper we give an attempt to this challenging topic by studying an American style option with strangle payoff, which was previously investigated by Chiarella and Ziogas [11] and Moraux [12] for single asset and constant volatility. We develop the lattice methods of Ritchken and Trevor [2] to the American strangle options with many underlying assets and multidimensional stochastic volatility GARCH models. We compare the lattice methods with the least square Monte-Carlo methods via several numerical examples.

2. Two-Dimensional Stochastic Volatility Models of American Strangles

Assume that the prices of two-dimensional assets

follow a two-dimensional GARCH model (see, e.g., Duan [13] for more explanation of the one-dimensional GARCH model). Consider

()

with i = 1,2, where

is the price of the ith asset corresponding to the standard Brown motion, qⁱ is the dividend rate for the ith asset,

is the volatility of the ith asset price,

, conditional on information at time t, is a standard normal random variable, r_f is the riskless rate of return over the period, and λ_i is the unit risk premium for the ith asset. Under the local risk-neutralized measure, the processes (1) are written as

()

with i = 1,2, where

, conditional on time t information, is a standard normal random variable with respect to the risk-neutralized measure, the parameters

, c^*,i in the model can be obtained by regression on the financial market, and

is the initial variance of asset i. Let

be a single-valued function of S_t. In this paper, we consider a two-dimensional assets American strangle option whose payoff at maturity T is defined by

()

in which K₁ and K₂, the strikes for American strangle′s call and put parts, satisfy K₁ < K₂.

3. Lattice Algorithms

Ritchken and Trevor [2] investigated the stochastic lattice methods for one-dimensional GARCH model. This paper intends to extend the methods to two-dimensional GARCH model. The aim of this paper is to design an algorithm that avoids an exponentially exploding number of states. Toward this goal, we begin by approximating the sequence of single period log normal random variables in (2) by a sequence of discrete random variables. In particular, assume the information set at date t is

, and let

. Then, viewed from date t,

, are normal random variables with conditional moments. Consider

()

We establish two discrete state Markov chains’ approximation,

, for the dynamics of the discrete time state variables that converge to the continuous state

. In particular, we approximate the sequence of conditional normal random variables by a sequence of discrete random variables. Given this period′s logarithmic price and conditional variance, the conditional normal distribution of the next period′s logarithmic price is approximated by a discrete random variable that takes on 2n + 1 values for each asset. The lattice we construct has the property that the conditional means and variances of one period returns match the true means and variances given in (4), and the approximating sequence of discrete random variables converges to the true sequence of normal random variables. For each asset, the gap between adjacent logarithmic prices is determined by a spacing parameter

for the logarithmic returns in such a way that all the approximating logarithmic prices are separated by

()

The size of these 2n + 1 jumps is restricted to integer multiples of

. Another important issue is to ensure valid probability values over the grid of 2n + 1 prices; the size of these jumps needs to be adjusted accordingly. This is efficiently handled with the inclusion of a jump parameter ηⁱ, which is an integer that depends on the level of the variance as follows:

()

Consequently, the resulting two-asset GARCH model is

()

for i = 1,2, where

()

and j = 0, ±1, ±2, …, ±n,

, i = 1,2. The probability distribution for

, conditional on

and

, is then given by

()

where

()

with j_u, j_m, j_d ≥ 0 such that n = j_u + j_m + j_d and j = j_u − j_d. Use the same lattice tree for assets S₁ and S₂ independently and assume each asset node has three possible paths to the next node: up, middle, and down. Then there are 9 possible combinations. The order of calculation is

, and

, which is illustrated by Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Two-asset GARCH tree.

The possibilities for the nine combinations are P¹(1)P²(1), P¹(1)P²(0), P¹(1)P²(−1), P¹(0)P²(1), P¹(0)P²(0), P¹(0)P²(−1), P¹(−1)P²(1), P¹(−1)P²(0), and P¹(−1)P²(−1). Then, the volatility pattern by restricting the storage of conditional variance to the minimum and maximum values at each node under the forward-building process needs to be constructed. At each node for each asset, the option prices over a grid of K points are evaluated, covering the state space of the variances from the minimum to the maximum for each asset. Let

and

represent the maximum and minimum variances that can be attained at node m for asset i. Option prices at this node are computed for K levels of variance ranging from the lowest to the highest at equidistant intervals. In particular,

representing the kth level of the variance at node (t, m) with k = 1, …, K is defined by an interpolation as follows:

()

where

()

For K = 3, the full volatility information at node (t, m) is described by Table 1.

Table 1. Full volatility information at node (t, m).

,
,
,
,
,
,
,
,
,

According to Wu [4], we have

()

where i = 1,2 represent the i asset, and

is the approximation volatility of asset i at time t, and ηⁱ is the jump parameter of asset i. Cakici and Topyan [3] modified the forward-building process and used interpolated variances only during the backward recursion to make the algorithm more efficient. They adopted only real node maximum and minimum variances, not the interpolated ones that fell between the maximum and minimum variances. It is intuitive to use interpolation for K points in the backward procedure. At the terminal time T, the two-asset American strangle option′s cash flow is

()

Let C_a,t(m, k) be the kth option price at the node (m, k), for k = 1,2, …, K, and the variance is

. Note that the boundary condition for a two-asset American strangle option with strike X which expires in period T is

()

We apply backward recursion to establish the option price at date 0. Consider a node (m, k) at time t. Then we compute the option price C_a,t(m, k) corresponding to variance

at the node. Given the variance

, we compute the appropriate jump parameter, ηⁱ for each asset, by (6). The successive nodes for this variance combination are ((t + 1, m + j¹η¹), (t + 1, m + j²η²)), where j¹ = 0, ±1, ±2, …, ±n and j² = 0, ±1, ±2, …, ±n. Equation (11) is used to compute the period (t + 1) variance for each of these nodes. Specifically, for the transition from the kth variance element of node (t, m) to node ((t + 1, m + j¹η¹), (t + 1, m + j²η²)), the period (t + 1) variance for each asset is given by

()

where j^1,2 represents the combination of j¹ and j². Linear interpolation of the two stored option prices corresponding to the two stored variance entries closest to

is used to obtain the option price corresponding to a variance of

when

is already chosen. Let L be an integer smaller than K defined via

()

The interpolated option price is

()

where

()

In this way an option price is identified for each of the (2n + 1)(2n + 1) jumps from node (t, m) with variance combination

. In each case, either node (t + 1, m + j^1,2η^1,2) contains a variance entry (and hence option value) that matches

, or the relevant information is interpolated from the closest two entries. We use the following formula to compute the unexercised option value

()

Denote the exercised value of the claim by

. For a two-asset American strangle option with strikes K₁ and K₂, K₁ < K₂,

()

The value of the claim at the kth entry of node (t, m) is then

()

The final option price, obtained by backward recursion of this procedure, is given by C_a,0(0,1).

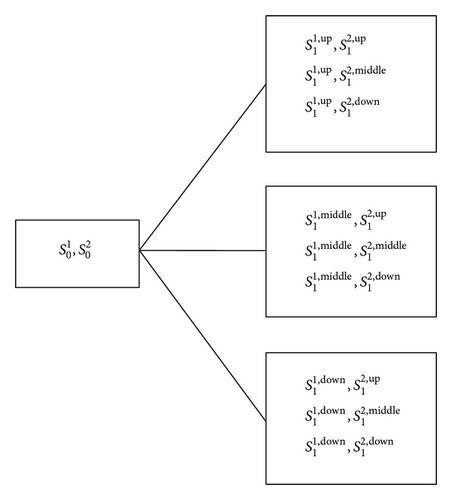
4. Numerical Examples

In this section, several examples are implemented using the lattice method in this paper and least square Monte-Carlo method (LSM) developed by Longstaff and Schwartz [14].

In Examples 1, 2, and 3, we focus on the single asset American strangle options under GARCH model where the convergence with respect to n and K are studied, respectively, in the first two examples, and the optimal exercise boundaries are drawn for the third example. In Examples 4 and 5, we compute the two-dimensional assets American strangle options.

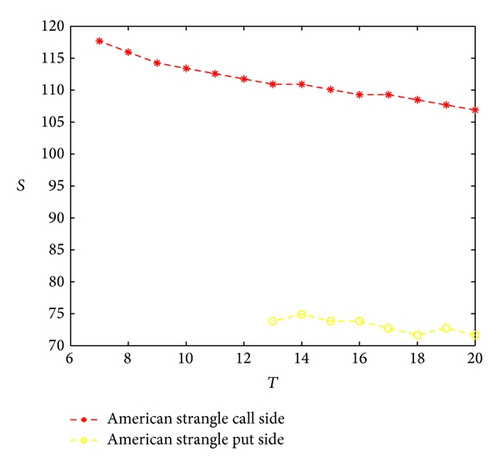
In Tables 2 and 3, the prices of the options using LSM with 5,000 paths are calculated and the intervals that the true prices fall into are provided. From the comparisons we confirm that the lattice methods developed in this paper are correct and reliable. Furthermore from Table 2 we observe that the lattice method converges as n goes larger and from Table 3 the lattice method converges as K goes larger. Figure 2 shows exercise and holding regions: the middle part is the holding region and the top and bottom parts are the exercise regions.

Table 2. Numerical results for Example 1.

T	n	Option prices with lattice	Option prices and intervals with LSM
	1	0.014987254820724	0.029606167588959
	2	0.030190542190626
5	4	0.030393224336490
	7	0.030981333835160
	10	0.031863879158063

	1	0.068487810335143	0.081499912354419
	2	0.081254039347033
7	4	0.083605936631716
	7	0.081680163494625
	10	0.080301350887482

	1	0.178948896057298	0.193857807991106
	2	0.192329465764766
10	4	0.195314383716280
	7	0.199868029599249
	10	0.193058780881166

Table 3. Numerical results for Example 2.

T	K	Option prices with lattice	Option prices and intervals with LSM
5	2	0.028187456298155	0.029606167588959
	4	0.029090524706680
	6	0.029930565933099
	10	0.030190542190626
	20	0.029391074539888
	40	0.029489977773055

10	2	0.197070210662258	0.193857807991106
	4	0.195700639175277
	6	0.196465071653130
	10	0.192329465764766
	20	0.193696054251151
	40	0.194423204241922

30	2	1.182560819901510	1.205198709585444
	4	1.197816540629624
	6	1.200350772727828
	10	1.202714267674711
	20	1.203407511987706
	40	1.203545193979154

Example 1. Consider single asset GARCH model with parameters r_f = 5%, q = 10%, β₀ = 6.575 × 10⁻⁶, β₁ = 0.9, β₂ = 0.04, S₀ = 100, h₀ = 0.0001096, K₁ = 105, K₂ = 95, γ = h₀, and c^* = 0. Fixing K = 20, we investigate the convergence behavior as n increases.

Example 2. Consider single asset GARCH model with the same parameters as Example 1. In this example, n = 5 and the sensitivity to the volatility space parameter, K, is explored.

Example 3. Consider single asset GARCH model with the same parameters as Example 1. Draw the figure of the optimal exercise boundaries for American strangle.

In Examples 4 and 5, we examine the stochastic lattice methods for pricing American strangle options under multiasset under stochastic volatility model where the convergence with n and K are studied. From the numerics in Tables 4 and 5, we confirm that the lattice methods for two-dimensional models are correct and reliable and the convergence of the lattice methods with respect to n and K is observed.

Table 4. Numerical results for Example 4.

T	n	Option prices with lattice	Option prices and interval with LSM
3	1	0.005974297	0.005065587636226
	2	0.004223692
	3	0.004502351
	4	0.005530355
	5	0.005040507

4	1	0.014427788	0.015018277749022
	2	0.014590056
	3	0.013984718
	4	0.017223364
	5	0.015988485

5	1	0.022129134	0.034841312405081
	2	0.030507636
	3	0.030853276
	4	0.035594538
	5	0.034694665

Table 5. Numerical results for Example 5.

T	K	Option prices with lattice	Option prices and intervals with LSM
3	2	0.005974297	0.005065587636226
	4	0.005974297
	6	0.005974297
	8	0.005974297
	10	0.005974297

4	2	0.014427788	0.015018277749022
	4	0.014427788
	6	0.014427788
	8	0.014427788
	10	0.014427788

5	2	0.02194509	0.034841312405081
	4	0.022129134
	6	0.022164226
	8	0.024355984
	10	0.024276964

Example 4. Consider two-asset American strangles with parameters r_f = 5%, q¹ = q² = 10%, , , , , , K₁ = 105, K₂ = 95, , and c^*,1 = c^*,2 = 0. Fixing K = 4, we investigate the convergence behavior as n increases.

Example 5. Consider the two-dimensional GARCH model with the same parameters as Example 4. Fixing n = 1, we study the sensitivity to the volatility space parameter K.

5. Conclusions

In this paper we studied pricing methods for stochastic volatility models of the American strangles with single asset and multiassets. Both lattice methods and LSM methods are developed and implemented. To the best of our knowledge, there are no results on the lattice methods for multidimensional stochastic volatility models. We first extended the stochastic lattice methods invented by Ritchken and Trevor [2] which are for one-dimensional GARCH models of American call to the multidimensional GARCH models of American strangles. Numerical examples confirm the correctness and reliability of the lattice methods. Future challenging works include the development of the lattice methods for multidimensional volatility models with correlations and recently developed models (e.g., [15]). One possible solution to the case of correlation is to adopt the idea (using moment-generating function) in [7]. However it needs to develop new techniques when the stochastic volatility models are involved. Furthermore, a dimensional-reduction technique should be developed to reduce the computational cost.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgment

The work was supported by the Fundamental Research Funds for the Central Universities (Grant no. JBK130401).

References

1 Heston S. L., A closed-form solution for options with stochastic volatility with applications to bond and currency options, Review of Financial Studies. (1993) 6, 327–343.
10.1093/rfs/6.2.327
Web of Science® Google Scholar
2 Ritchken P. and Trevor R., Pricing options under generalized GARCH and stochastic volatility processes, Journal of Finance. (1999) 54, no. 1, 377–402, 2-s2.0-0009081815.
10.1111/0022-1082.00109
Web of Science® Google Scholar
3 Cakici N. and Topyan K., The GARCH option pricing model: a lattice approach, Quantitative Finance. (2000) 2, 432–442.
Google Scholar
4 Wu C.-C., The GARCH option pricing model: a modification of lattice approach, Review of Quantitative Finance and Accounting. (2006) 26, no. 1, 55–66, 2-s2.0-31444448881, https://doi.org/10.1007/s11156-006-7033-2.
10.1007/s11156-006-7033-2
Web of Science® Google Scholar
5 Akyildirim E., Dolinsky Y., and Soner H., Approximating stochastic volatility by recombinant trees, http://arxiv.org/abs/1205.3555v1.
Google Scholar
6 Boyle P., A lattice framework for option pricing with two state variables, Journal of Financial and Quantitative Analysis. (1988) 23, 1–2.
10.2307/2331019
CAS PubMed Web of Science® Google Scholar
7 Boyle P., Evnine J., and Gibbs S., Numerical evaluation of multivariate contingent claims, Review of Financial Studied. (1989) 2, 241–250.
10.1093/rfs/2.2.241
Web of Science® Google Scholar
8 Chen R.-R., Chung S.-L., and Yang T. T., Option pricing in a multi-asset, complete market economy, Journal of Financial and Quantitative Analysis. (2002) 37, no. 4, 649–666, 2-s2.0-0036924937.
10.2307/3595015
Web of Science® Google Scholar
9 Gamba A. and Trigeorgis L., An improved binomial lattice method for multi-dimensional options, Applied Mathematical Finance. (2007) 14, no. 5, 453–475, https://doi.org/10.1080/13504860701532237, MR2378982.
10.1080/13504860701532237
Google Scholar
10 Moon K.-S., Kim W.-J., and Kim H., Adaptive lattice methods for multi-asset models, Computers & Mathematics with Applications. (2008) 56, no. 2, 352–366, https://doi.org/10.1016/j.camwa.2007.12.008, MR2442658.
10.1016/j.camwa.2007.12.008
Web of Science® Google Scholar
11 Chiarella C. and Ziogas A., Evaluation of American strangles, Journal of Economic Dynamics & Control. (2005) 29, no. 1-2, 31–62, https://doi.org/10.1016/j.jedc.2003.04.010, MR2115100.
10.1016/j.jedc.2003.04.010
Web of Science® Google Scholar
12 Moraux F., On perpetual American strangles, Journal of Derivatives. (2009) 16, no. 4, 82–97, 2-s2.0-77956312553, https://doi.org/10.3905/JOD.2009.16.4.082.
10.3905/JOD.2009.16.4.082
Web of Science® Google Scholar
13 Duan J.-C., The GARCH option pricing model, Mathematical Finance. (1995) 5, no. 1, 13–32, https://doi.org/10.1111/j.1467-9965.1995.tb00099.x, MR1322698.
10.1111/j.1467-9965.1995.tb00099.x
Google Scholar
14 Longstaff F. A. and Schwartz E. S., Valuing American options by simulation: a simple least-squares approach, Review of Financial Studies. (2001) 14, no. 1, 113–147, 2-s2.0-0035578679.
10.1093/rfs/14.1.113
Web of Science® Google Scholar
15 Huang C. X., Gong X., Chen X., and Wen F. H., Measuring and forecasting volatility in Chinese stock market using HAR-CJ-M model, Abstract and Applied Analysis. (2013) 2013, 13, 143194, https://doi.org/10.1155/2013/143194.
10.1155/2013/143194
Google Scholar

Citing Literature

All articles

Lattice Methods for Pricing American Strangles with Two-Dimensional Stochastic Volatility Models

Abstract

1. Introduction

2. Two-Dimensional Stochastic Volatility Models of American Strangles

3. Lattice Algorithms

4. Numerical Examples

5. Conclusions

Conflict of Interests

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Lattice Methods for Pricing American Strangles with Two-Dimensional Stochastic Volatility Models

Abstract

1. Introduction

2. Two-Dimensional Stochastic Volatility Models of American Strangles

3. Lattice Algorithms

4. Numerical Examples

5. Conclusions

Conflict of Interests

Acknowledgment

References

Citing Literature

Figures

References

Related

Information